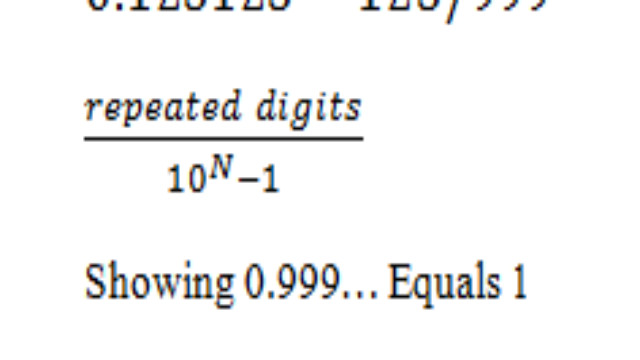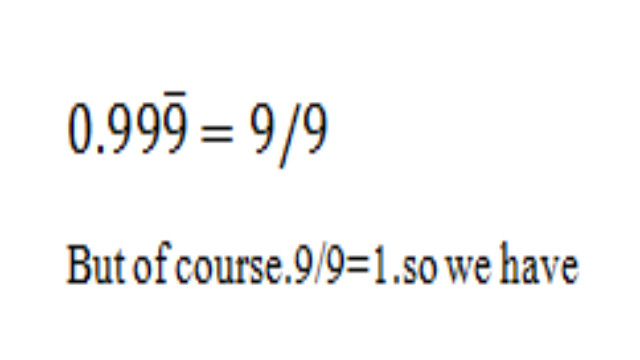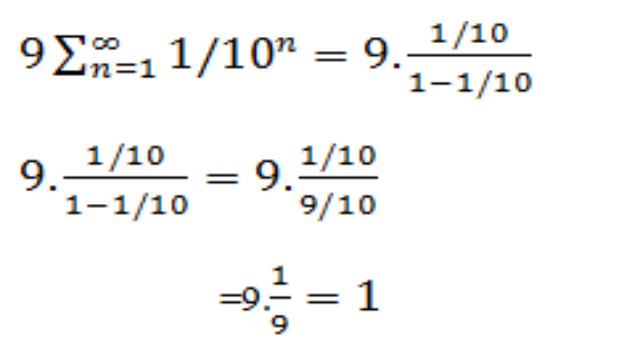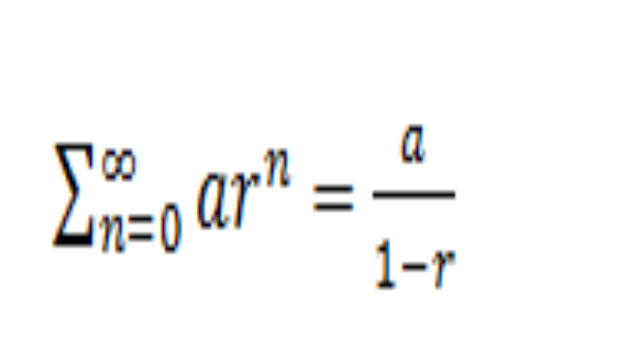Why Does 0.999… Equal 1?
क्यों 0.999 … बराबर 1 ? का परिचय (Introduction to Why Does 0.999… Equal 1?):
- क्यों 0.999 … बराबर 1 ?(Why Does 0.999… Equal 1?) का तात्पर्य है कि यह अनंत की ओर अग्रसर है जो एक का ही विस्तारित रूप है.अनंत का एक अर्थ यह भी है कि एक को दर्शाने का पाजिटिव तरीका है.जबकि शून्य के दवारा दर्शाना निगटिव तरीका है.
- आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
क्यों 0.999 … बराबर 1 ?(Why Does 0.999… Equal 1?)
- केवल घोड़े की नाल, हाथ हथगोले और गणित में गिनती बंद करें ???
Also Read This Article:Top 10 unsung geniuses
1.क्या? बिल्कुल नहीं?!! मैं गंभीर नहीं हो सकता, क्या मैं कर सकता हूँ? (So here’s what you need to know):
- यदि आप गणितीय परिशुद्धता से निराश हो जाते हैं, तो आज आपका भाग्यशाली दिन है क्योंकि इस प्रकाशन के इतिहास में पहली बार वास्तव में गणितीय रूप से सटीक है!
- मैं आपको यह दिखाने जा रहा हूं कि बुनियादी गणित के साथ आप अपने दोस्तों को कैसे दिखा सकते हैं कि दोहराए जाने वाला दशमलव 0.999 … वास्तव में 1 के बराबर है।
- हां, आपने मुझे सही सुना। हम दिखा सकते हैं कि यह बिना किसी कल्पना के सच है। कोई कैलकुलस, कोई सीमा नहीं, कोई उन्नत अवधारणा नहीं है। तो अंदर कूदने दो!
- कैसे भिन्न के रूप में दशमलव को दोहराते हुए व्यक्त करें
- कितने लोगों को यह एहसास नहीं है कि आप किसी भी दोहराए जाने वाले दशमलव को आसानी से एक अंश के रूप में लिख सकते हैं।
Also Read This Article:A viral mathematics question
इसलिए यहां आपको जानना आवश्यक है।(So here’s what you need to know):
- यदि आपके पास एकल-अंक दोहराने का मूल्य है, तो इस तरह से 9 के भाजक पर दोहराव अंक लिखें:
- यदि आपके पास 2 अंकों का दोहराव है, तो 99 के हर पर दोहराए गए अंकों को लिखें।
- यदि आपके पास 3 अंकों का दोहराव है, तो 999 के हर पर दोहराए गए अंकों को लिखें।
- नमूना देखो
Also Read This Article:0.999…
N दोहराए गए अंकों को देखते हुए, सूत्र है (Given N repeating digits, the formula is):
- 0.999 दिखा रहा है … बराबर 1
- ठीक है, यहाँ हम चलते हैं! इसके समकक्ष अंश के बराबर 0.999… सेट करके शुरू करें।
- लेकिन निश्चित रूप से, 9 ÷ 9 = 1. तो हमारे पास है:
- और हम कर चुके हैं छोटा एवं सुन्दर।
- अभी भी नहीं समझा?(Still Not Convinced?)-
- यदि आप अभी भी सोच रहे हैं कि यह कैसे सच हो सकता है, तो मैं आपको महसूस करता हूं।
- यह पूरी तरह से जवाबी कार्रवाई है।
- यह मनमौजी है।
- मैं प्रस्ताव कर रहा हूं कि 9 को 0.999 के अंत तक जोड़कर … न केवल यह करीब और 1 के करीब हो रहा है, लेकिन यह 1 है !?
- यह देखने का एक और तरीका है
- \frac{1}{3}=0.33333 के बराबर है … और \frac{2}{3}=0.66666 के बराबर है … इसलिए \frac{1}{3}+\frac{2}{3} को 0.3333 … + 0.6666 के बराबर होना चाहिए, है ना?
\frac{1}{3}+\frac{2}{3}=0.3333...
दोनों ओर योग करें और वहाँ फिर से है!
1=0.99999…
मेरे गणित के शौकीन इस समय शायद थोड़े निराश हैं क्योंकि यह अभी बहुत आसान है। - तो यह आसान है, जैसा कि वे गणित की दुनिया में कहते हैं, तुच्छ।
- मैं आपकी बात सुनता हूं। मैं अपने दिन में भी कुछ अधिक गणित के लिए तरस रहा हूँ। इसलिए यदि आप थोड़ी देर के आसपास रहना चाहते हैं तो मैं आपको दिखाता हूं कि यह एक अच्छी श्रृंखला के साथ क्यों सच है। आप जानते हैं कि कुछ फैंसी गणित मैंने कहा था कि हम आज नहीं करने जा रहे हैं, लेकिन मुझे लगता है कि यह इसके लायक होने जा रहा है।
अनंत श्रृंखला दृष्टिकोण (The Infinite Series Approach):
- आइए 0.999 को तोड़कर शुरुआत करते हैं … जो स्थान मूल्य का प्रतिनिधित्व करता है।
यदि आप अपने प्राथमिक स्कूल के दिनों के बारे में सोचते हैं, तो आपको याद होगा कि कोई शिक्षक आपको स्थान का मूल्य समझा रहा है और कुछ कह रहा है,
372=3 hundreds+7 tens+2 ones
हम 0.999… को इस तरह से शुरुआत कर सकते हैं:
9 tenths +9 hundredths + 9 thousandths +….
या भिन्नों के रूप में:
\frac{9}{10}+\frac{9}{100}+\frac{9}{1000}+\frac{9}{10,000}+\frac{9}{100,000} +...
यदि हम पहले 5 मूल्यों को जोड़ते हैं, तो हमें 0.99999 मिलते हैं और अगर हम दशमलव विस्तार लिखते रहे तो हम इसे अनंत तक लिख सकते हैं और सटीक मूल्य 0.999 प्राप्त कर सकते हैं…। - अनंत तक दशमलव विस्तार को मैन्युअल रूप से लिखना संभव नहीं है, इसलिए इसके लिए आशुलिपि है।
- 9 फैक्टरिंग करके शुरू करें।
9(\frac{1}{10}+\frac{1}{100}+\frac{1}{1000}+\frac{1}{100,000}+...) - फिर 10 की शक्तियों के रूप में हर को फिर से लिखना।
- अब अनंत योग का प्रतिनिधित्व करने के लिए सिग्मा नोटेशन का उपयोग करें।
- सिग्मा नोटेशन पर साइड नोट: यदि आप सिग्मा नोटेशन के लिए नए हैं, तो मैं इसे आपके लिए तोड़ दूंगा। ग्रीक अक्षर सिग्मा ∑ का प्रयोग गणित में बार-बार जोड़ने के लिए किया जाता है।
- आपके योग में पहला मान n के लिए पहले संकेतित मान में प्लगिंग द्वारा उत्पन्न होता है, जो ∑ के नीचे देखकर पाया जाता है। इस स्थिति में, वह मान n = 1 है, इसलिए हमें (\frac{1}{10}) value मिलता है।
- अगला मान प्राप्त करने के लिए आप अगले पूर्णांक में प्लग करें, n = 2, पाने के लिए (\frac{1}{10})। फिर (= 10) प्राप्त करने के लिए n = 3 में प्लग करें, और इसी तरह। ऐसा तब तक करते रहें जब तक आपको। सिंबल से ऊपर का मूल्य न मिल जाए। इस मामले में, यह अनंत है, इसलिए इसका कोई अंत नहीं है।
- और हां, इन सभी उत्पन्न मूल्यों को एक साथ जोड़ दिया जाता है और, हमारे मामले में, पूरे योग को 9 से गुणा किया जाता है।
- हमारे सारांश में शर्तों के बारे में सोचने का एक और तरीका यह है कि प्रत्येक क्रमिक शब्द पिछले शब्द को एक सामान्य अनुपात से गुणा करके प्राप्त किया जाता है।
- इसका मतलब है कि हमारे पास एक ज्यामितीय श्रृंखला है जो \frac{a}{1 - r} में परिवर्तित होती है, जहां श्रृंखला में पहला मान a और r वह अनुपात है जिसे हम अगले शब्द को प्राप्त करने के लिए गुणा करते हैं।
- एक अनंत ज्यामितीय श्रृंखला के लिए सूत्र
एक श्रृंखला में रूपांतरण का सीधा सा मतलब है कि श्रृंखला एक विशिष्ट मान के करीब और करीब आती रहेगी, क्योंकि आप श्रृंखला में अधिक से अधिक शब्द जोड़ते हैं। श्रृंखला अनंत रूप से अभिसरण मूल्य के करीब हो रही है। अनंत पैमाने पर, अभिसरण समानता बन जाता है।
हमारे मामले में, हम (\frac{1}{10}) से शुरू करते हैं और हर बार (\frac{1}{10}) से गुणा करते हैं, इसलिए a और r=(\frac{1}{10}) दोनों।
- A = (\frac{1}{10}) और r = (\frac{1}{10}) के बाद, हम a और r को जोड़ सकते हैं और योग को n = 1 से समायोजित कर सकते हैं, जो इस समस्या के लिए हमारे मूल योग से आसानी से मेल खाता है।
दाहिने हाथ की ओर अंकगणित पूरा करें।
अब हमने औपचारिक रूप से दिखाया है कि 0.999… 1 के बराबर या बराबर होता है। - अंतिम विचार और प्रेरणा
यदि यह आपको अजीब लगता है, तो यह अच्छा है! आप जानते हैं कि दो अलग-अलग संख्याएँ, वास्तव में अलग-अलग संख्याएँ होनी चाहिए। इस समस्या की प्रति-सहज प्रकृति उस अनजानता से अंतर्निहित है जो अनंत के साथ काम करने में साथ देती है। - यहां तक कि इस तरह की एक साधारण समस्या में भी, आप इस बात को सीमित कर रहे हैं कि मानव मस्तिष्क में किस पैमाने पर ठोस है जो हमारी समझ से परे है। परिमित प्राणियों के रूप में हम अनंत या हमेशा की अवधारणा को समझने में समझ सकते हैं, लेकिन वास्तव में इसका अनुभव कभी नहीं कर सकते। जिसका अर्थ है कि अक्सर हम अपने परिमित दुनिया में जो कुछ भी जानते हैं, वह अनंत स्तर पर अलग व्यवहार करते हैं।
- आसानी से खोजे जाने योग्य और प्रतिलिपि प्रस्तुत करने योग्य गणित से संक्रमण को स्वीकार करना जिसे केवल हमारे दिमाग में परीक्षण और कल्पना किया जा सकता है, गणित की सुंदरता और आश्चर्य का हिस्सा है।
- इसलिए आज के सबक को अंकित मूल्य पर न लें और इसे बंद कर दें।
- आप और सही समझ के बीच कोहरे की एक परत होने दें। अपने दिमाग को इस तथ्य से उड़ा दें कि अनन्तता अजीब व्यवहार करती है। और यह आपको अधिक समझ और सबसे अधिक गणित के लिए तरसने दें।
- उपर्युक्त आर्टिकल में क्यों 0.999 … बराबर 1 ?(Why Does 0.999… Equal 1?) के बारे में बताया गया है.
Why Does 0.999… Equal 1?
क्यों 0.999 … बराबर 1 ?
(Why Does 0.999… Equal 1?)
Why Does 0.999… Equal 1?
क्यों 0.999 … बराबर 1 ?(Why Does 0.999… Equal 1?) का तात्पर्य है कि यह अनंत की ओर अग्रसर है
जो एक का ही विस्तारित रूप है.अनंत का एक अर्थ यह भी है कि एक को
दर्शाने का पाजिटिव तरीका है.जबकि शून्य के दवारा दर्शाना निगटिव तरीका है.
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
About my self
Lekhak Ke Baare Mein (About the Author)
**Satyam Narain Kumawat**
**Website Name:Satyam Mathematics**
*Owner:satyamcoachingcentre.in*
*Sthan:Manoharpur,Jaipur (Rajasthan)*
**Teaching Mathematics aur Anya Anubhav**
***Shiksha:**B.sc.,B.Ed.,(M.sc. star Ke Mathematics Ko Padhane ka Anubhav),B.com.,M.com. Ke vishayon Ko Padhane ka Anubhav,Philosophy,Psychology,Religious,sanskriti Mein Gahri Ruchi aur Adhyayan
***Anubhav:**phichale 23 varshon se M.sc.,M.com.,Angreji aur Vigyan Vishayon Mein Shikshaka Ka Lamba Anubhav
***Visheshagyata:*Maths,Adhyatma (spiritual),Yog vishayon ka vistrit Gyan*
****In Brief:I have read about M.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 23 years teaching experience upto M.sc. ,M.com.,English and science.
About Author
Satyam
About my self Lekhak Ke Baare Mein (About the Author) **Satyam Narain Kumawat** **Website Name:Satyam Mathematics** *Owner:satyamcoachingcentre.in* *Sthan:Manoharpur,Jaipur (Rajasthan)* **Teaching Mathematics aur Anya Anubhav** ***Shiksha:**B.sc.,B.Ed.,(M.sc. star Ke Mathematics Ko Padhane ka Anubhav),B.com.,M.com. Ke vishayon Ko Padhane ka Anubhav,Philosophy,Psychology,Religious,sanskriti Mein Gahri Ruchi aur Adhyayan ***Anubhav:**phichale 23 varshon se M.sc.,M.com.,Angreji aur Vigyan Vishayon Mein Shikshaka Ka Lamba Anubhav ***Visheshagyata:*Maths,Adhyatma (spiritual),Yog vishayon ka vistrit Gyan* ****In Brief:I have read about M.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 23 years teaching experience upto M.sc. ,M.com.,English and science.
