1.त्रिभुज के कोण क्या हैं? (What Are The Angles Of A Triangle?),त्रिभुज के गुणधर्म क्या हैं? (What Are The Properties of A Triangle?):

त्रिभुज के कोण क्या हैं? (What Are The Angles Of A Triangle?)-यदि समतल में कोई असंरेख बिन्दु लें और स्केल द्वारा दो-दो बिन्दुओं को लेकर रेखाखण्ड खींचे तो कुल तीन रेखाखण्ड खींचे जा सकते हैं।इस प्रकार तीन रेखाखण्डों‌ से घिरी हुई आकृति को त्रिभुज कहते हैं।
तीन असंरेख बिन्दुओं में से दो-दो को मिलाने से बने तीन रेखाखण्डों के सम्मिलन से बनी बन्द आकृति को त्रिभुज कहते हैं।
चित्र में तीन असंरेख बिन्दुओं A,B एवं C को मिलाया गया है और इस प्रकार ‌तीन रेखाखण्डों AB,BC एवं CA से घिरी हुई आकृति ABC को त्रिभुज कहते हैं।त्रिभुज शब्द के लिए संकेत \triangle का प्रयोग करते हैं अर्थात् त्रिभुज ABC को \triangle ABC लिखते हैं।

उन तीन बिन्दुओं को जिन्हें मिलाने से एक त्रिभुज बनता है, त्रिभुज के शीर्ष बिन्दु या शीर्ष (Vertices) कहते हैं। त्रिभुज के तीन रेखाखण्डों को उसकी भुजाएं (Sides) कहते हैं।त्रिभुज के तीन रेखाखण्डों से शीर्ष बिन्दुओं पर बने तीन कोणों को त्रिभुज के कोण कहते हैं।
चित्र से स्पष्ट है कि \triangle ABC में
(1.)बिन्दु A,B एवं C उसके शीर्ष हैं।
(2.)रेखाखण्ड AB,BC एवं‌ CA उसकी भुजाएं हैं।
(3.) \angle CAB (या \angle A),\angle ABC (या \angle B),\angle BCA(या \angle C) त्रिभुज के कोण हैं।

यदि \triangle ABC की भुजाओं को क्रमानुसार आगे बढ़ाया जाए तो बढ़ी हुई भुजा और अन्य संलग्न भुजा के बीच के कोण को त्रिभुज का बहिष्कोण कहते हैं।
चित्र में अंकित \angle 1,\angle 2 तथा \angle 3 त्रिभुज के बहिष्कोण हैं।\angle 4,\angle 5 एवं \angle 6 त्रिभुज के अन्त:कोण हैं।त्रिभुजों को भुजाओं के आधार पर वर्गीकृत किया जा सकता है।
भुजाओं के आधार पर त्रिभुजों का वर्गीकरण या त्रिभुजों के प्रकार (Classification of Triangles by Sides Or Types of Triangles):
(1.)विषमबाहु त्रिभुज (Scalene Triangle):
जिस त्रिभुज की तीनों भुजाएं अलग-अलग माप की हो उसे विषमबाहु त्रिभुज कहते हैं।चित्र में \triangle ABC एक विषमबाहु त्रिभुज है।

(2.)समद्विबाहु त्रिभुज (Isosceles Triangle):
यदि किसी त्रिभुज की दो भुजाएं समान माप की हों तो उसे समद्विबाहु त्रिभुज कहा जाता है।चित्र में \triangle PQR एक समद्विबाहु त्रिभुज है इसमें PQ=PR है।

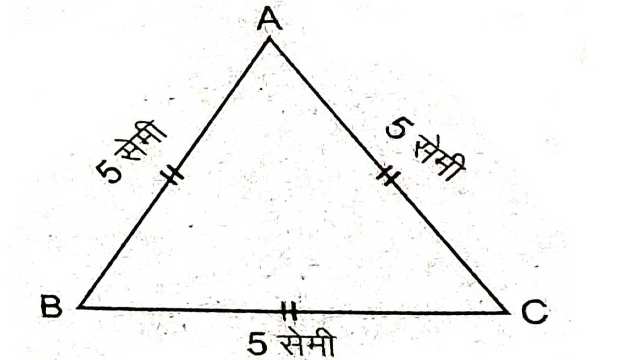
(3.)समबाहु त्रिभुज (Equilateral Triangle):
जिस त्रिभुज में सभी भुजाएं समान माप की हो,उसे समबाहु त्रिभुज कहते हैं।चित्र में \triangle ABC एक समबाहु त्रिभुज है इसमें AB=BC=CA है।

कोणों के आधार पर त्रिभुजों का वर्गीकरण या कोणों के आधार पर त्रिभुजों के प्रकार (Classification of Triangles by Angeles Or Types of Triangles by Angeles):
(1.)न्यून कोण त्रिभुज (Acute Angle Triangle):
जिस त्रिभुज का प्रत्येक कोण न्यून कोण हो उसे न्यून कोण त्रिभुज कहते हैं।चित्र में \triangle PQR एक न्यून कोण त्रिभुज है क्योंकि इसमें \angle P, \angle Q तथा \angle R न्यून कोण हैं।

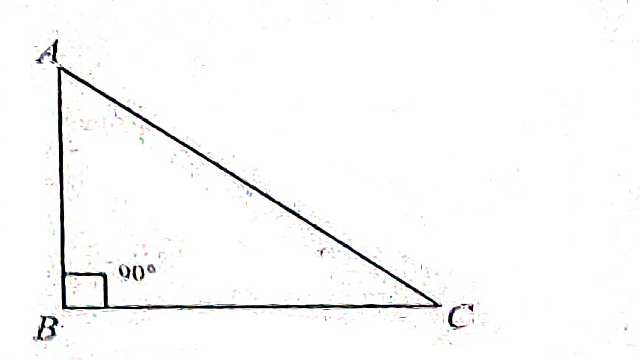
(2.)समकोण त्रिभुज (Right Angled Triangle):
जिस त्रिभुज का एक कोण 90° के बराबर हो उसे समकोण त्रिभुज कहते हैं।चित्र में \triangle ABC एक समकोण त्रिभुज है क्योंकि इसमें \angle B=90° है।

(3.)अधिककोण त्रिभुज (Obtuse Angled Triangle):
जिस त्रिभुज में कोई कोण 90° से अधिक हो उसे अधिककोण त्रिभुज कहते हैं।चित्र में \triangle PQR एक अधिक कोण त्रिभुज है क्योंकि इसमें \angle PQR ,90° से अधिक है।त्रिभुज के तीनों कोणों की माप को जोड़ने पर योगफल सदैव 180° प्राप्त होता।नीचे इसी ज्यामितीय तथ्य को सिद्ध किया गया है।

प्रमेय (Theorem):1.त्रिभुज के तीनों कोणों का योगफल दो समकोण के बराबर होता है।
(The sum of the three angles of a triangle is equal to two right angles).
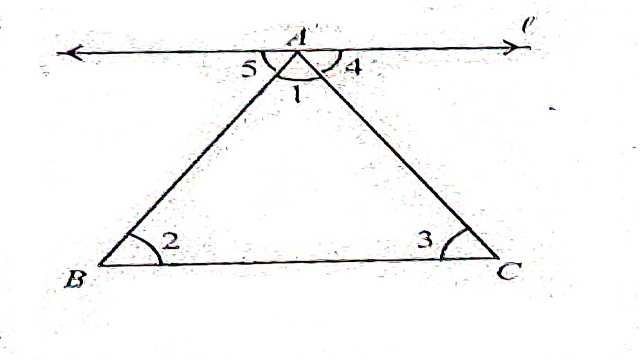
दिया है (Given):एक \triangle ABC में उसके कोणों \angle 1, \angle 2 तथा \angle 3 द्वारा अंकित किया गया है।

सिद्ध करना है (To Prove):\angle 1+ \angle 2+ \angle 3=180°
रचना (Construction):\triangle ABC के शीर्ष A से गुजरती हुई एक सरल रेखा l,भुजा BC के समान्तर खींची।
उपपत्ति (Proof):BC \parallel l है।
अतः\angle 2= \angle 5 (एकान्तर कोण)…..(1)
एवं \angle 3= \angle 4 (एकान्तर कोण)……(2)
समीकरण (1) और (2) को जोड़ने पर-

\Rightarrow \angle 2 +\angle 3=\angle 5 +\angle 4 \cdots(3)
(3) के दोनों पक्षों में \angle 1 जोड़ने पर-

\Rightarrow \angle 1+ \angle 2 +\angle 3=\angle 1+ \angle 5 +\angle 4 \cdots(4)
रैखिक कोण युग्म अभिगृहीत से

\angle 1+ \angle 5 +\angle 4=180° \cdots(5)
(4) व (5) से-

\Rightarrow \angle 1+ \angle 2 +\angle 3=180°
उपप्रमेय (Corollary):1.यदि किसी त्रिभुज की एक भुजा को बढ़ा दी जाए तो इस प्रकार बना बहिष्कोण अन्तराभिमुख अन्त: कोणों के योग के बराबर होता है।
(If one side of a triangle is extended, the exterior angle thus formed is equal to the sum of the interior opposite angles).
\triangle के तीनों अन्त: कोणों का योग 180° होता है

\angle 1+ \angle 2 +\angle 3=180° \cdots(1)
रैखिक कोण युग्म अभिगृहीत से

\angle 3 +\angle 4=180° \cdots(2)
समीकरण (1) व (2) से-

\Rightarrow \angle 1+ \angle 2 +\angle 3=\angle 3 +\angle 4 \\ \Rightarrow \angle 1+ \angle 2 =\angle 4
उपप्रमेय (Corollary):2.किसी त्रिभुज में एक बहिष्कोण प्रत्येक अन्तराभिमुख अन्त:कोण से बड़ा होता है।
(In a triangle, one of the exterior angle is larger than each of the interior opposite angles).
उपर्युक्त प्रमेय में \angle 4= \angle 1+ \angle 2   (उपप्रमेय 1 से)
\Rightarrow \angle 4 > \angle 1 एवं \angle 4 > \angle 2
उपप्रमेय (Corollary):3.एक समकोण त्रिभुज में,समकोण ही सबसे बड़ा कोण होता है।
(In a right angled triangle,the right angle is the largest angle).
\because  एक त्रिभुज के तीनों कोणों का योगफल=180°
एक समकोण+दो अन्य कोणों का योग=180°
दो अन्य कोणों का योग=90°
\Rightarrow शेष दोनों कोणों में प्रत्येक न्यून कोण हैं।
\Rightarrow समकोण,शेष दोनों न्यून कोणों से बड़ा है।
उपप्रमेय (Corollary):4.किसी चतुर्भुज के चारों कोणों का योगफल चार समकोण के बराबर होता है।
(The sum of the four angles of a quadrilateral is four right angles).
चित्र में ABCD एक चतुर्भुज है।इसके चार कोण \angle A, \angle B, \angle C एवम् \angle D है।AC रेखा चतुर्भुज को दो त्रिभुजों में बांट रही है।

\triangle ABC में

\angle 1+ \angle 2 +\angle 3=180° \cdots(1)
एवं \triangle ADC में

\angle 4+ \angle 5 +\angle 6=180° \cdots(2)
(1) तथा (2) से-

\angle 1+ \angle 2 +\angle 3+\angle 4+ \angle 5 +\angle 6=360° \\ \Rightarrow (\angle 1+ \angle 4) +\angle 2+(\angle 3+ \angle 5) +\angle 6=360° \\ \Rightarrow \angle A+ \angle B +\angle C+\angle D=360°
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:-Mid Point Theorem

2.त्रिभुज के कोण क्या हैं के उदाहरण (What Are The Angles Of A Triangle‌ Examples),त्रिभुज के गुणधर्म क्या हैं के उदाहरण (What Are The Properties of A Triangle Examples):

Example-1.दिए गए चित्र से \triangle ABC के तीनों कोण ज्ञात कीजिए।
Solution–\angle ACB=\angle DCE(शीर्षाभिमुख कोण)

\angle ACB=53° \\ \angle FAC+\angle BAC=180°(रैखिक कोण युग्म से)

\Rightarrow 112° +\angle BAC=180° \\ \Rightarrow \angle BAC=180°-112°  \\ \Rightarrow \angle BAC=68°
\triangle ABC में
\angle BAC+\angle B+ \angle ACB=180° (त्रिभुज के तीनों कोणों का योग)

\Rightarrow 68°+\angle B+ 53°=180° \\ \Rightarrow 121°+\angle B=180° \\ \Rightarrow \angle B=180°-121° \\ \Rightarrow \angle B=59°
Example-2.चित्र में \triangle ABC एक समबाहु त्रिभुज है।चित्र से \angle x, \angle y और \angle z के मान ज्ञात कीजिए।
Solution–\triangle ABC समबाहु त्रिभुज है अतः

\angle ABC= \angle BAC= \angle ACB=60°
\triangle APB में
\angle PAB + \angle APB=\angle ABC (बहिष्कोण=अन्तराभिमुख कोणों का योग)

\Rightarrow 22°+\angle x=60° \\  \Rightarrow \angle x=60°-22° \\ \Rightarrow \angle x=38°\\  \angle ABC+\angle ABP=180° (रैखिक कोण युग्म से)

\Rightarrow 60°+ \angle z=180° \\ \Rightarrow \angle z=180°- 60° \\ \Rightarrow \angle z=120°

\triangle ACQ में

\angle CAQ+ \angle AQC= \angle ACB (बहिष्कोण=अन्तराभिमुख कोणों का योग)

\Rightarrow 38°+ \angle y=60° \\ \Rightarrow  \angle y=60° -38° \\ \Rightarrow  \angle y=22° \\ \angle x=38°, \angle y=22° और \angle z=120°
Example-3.चित्र में \triangle ABC की भुजाएं AB और AC को क्रमशः E और D तक बढ़ाया गया है।यदि \angle CBE और \angle BCD के समद्विभाजक क्रमशः BO और CO बिन्दु O पर मिलते हैं तो सिद्ध कीजिए कि \angle BOC=90°-\frac{ \angle x }{2}  है।
Solution-दिया है (Given):\angle CBE तथा \angle BCD के समद्विभाजक क्रमशः BO और CO बिन्दु O पर मिलते हैं।

सिद्ध करना है (To Prove):\angle BOC=90°-\frac{ \angle x }{2}
उपपत्ति (Proof): \triangle ABC में
\angle A+ \angle ABC+\angle ACB=180° \\  \Rightarrow \angle x +\angle y+\angle z=180° \\ \Rightarrow \angle y+\angle z=180° -\angle x \cdots(1) \\ \angle ABC+\angle CBE=180° (रैखिक कोण युग्म से)

\angle y+\angle CBE=180° \\ \Rightarrow \angle CBE=180°-y° \cdots(2) \\ \angle ACB+\angle BCD=180° (रैखिक कोण युग्म से)

\angle z+\angle BCD=180° \\ \Rightarrow \angle BCD=180°-z° \cdots(3)
(2) व (3) को जोड़ने पर-

\angle CBE +\angle BCD=180°-y°+180°-z° \\ \Rightarrow \frac{1}{2} \left(\angle CBE +\angle BCD\right)=\frac{1}{2} \left[ 360°-\left(y°+z°\right)\right] \\ \Rightarrow \frac{1}{2} \angle CBE +\frac{1}{2} \angle BCD=180°-\frac{1}{2}  \left(y°+z°\right) \\ \Rightarrow \angle CBO +\angle BCO=180°-\frac{1}{2}  \left(y°+z°\right) \cdots(4)
[\because  BO तथा CO क्रमशः \angle CBE व \angle BCD के समद्विभाजक हैं]
समीकरण (1) व (4) से-

\Rightarrow \angle CBO +\angle BCO=180°-\frac{1}{2}  \left(180°-x°\right) \\ \Rightarrow \angle CBO +\angle BCO=180°-90°+\frac{1}{2} x° \\ \Rightarrow \angle CBO +\angle BCO=90°+\frac{1}{2} \angle x° \cdots(5)

\triangle BOC में

\angle CBO +\angle BCO+\angle BOC=180°\\ \angle CBO +\angle BCO=180°-\angle BOC \cdots(6)
समीकरण (5) व (6) से-

\Rightarrow 180°-\angle BOC=90°+\frac{1}{2} \angle x \\ \Rightarrow \angle BOC= 180°-90°-\frac{\angle x}{2} \\  \Rightarrow \angle BOC=90°-\frac{\angle x}{2}
Example-4.चित्र में \angle P=52°और \angle PQR=64° है।यदि QO और RO क्रमशः \angle PQR और \angle PRQ के समद्विभाजक हैं तो \angle x और \angle y के मान ज्ञात कीजिए।
Solution–\triangle PQR में

\angle P+ \angle PQR+ \angle PRQ=180° \\ \Rightarrow 52°+64°+\angle PRQ=180° \\ \Rightarrow 116°+\angle PRQ=180° \\ \Rightarrow \angle PRQ=180°-116° \\ \Rightarrow \angle PRQ=64° \\  \Rightarrow \angle y=\frac{1}{2} \angle PRQ [OR, \angle PRQ का समद्विभाजक है]
\Rightarrow \angle y=\frac{1}{2} \times 64° \\ \Rightarrow \angle y=32° \\ \angle PQR=64° \\ \Rightarrow \angle OQR=\frac{1}{2} \angle PQR [\because QO, \angle PQR का समद्विभाजक है]

\Rightarrow \angle OQR=\frac{1}{2} \times 64° \\ \Rightarrow \angle OQR=32°

\triangle QOR में

\angle QOR+\angle OQR+\angle ORQ=180° \\ \Rightarrow 32°+\angle OQR+32°=180° \\ \Rightarrow \angle x=180°-64° \\ \Rightarrow \angle x=116°,\angle y=32°
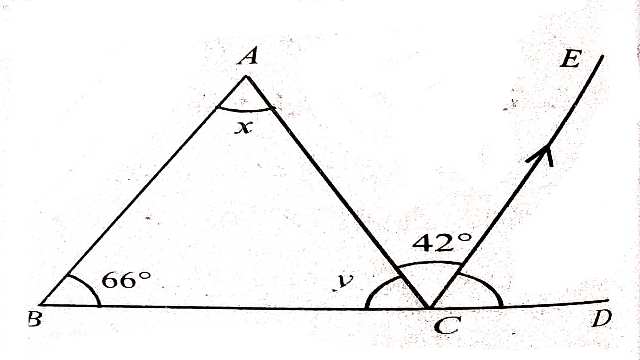
Example-5.चित्र में यदि AB \parallel DE ,\angle BAC=35° और \angle CDE=53°  है तो \angle DCE ज्ञात कीजिए।
Solution–AB \parallel DE \\ \angle DEC=\angle BAC(एकान्तर कोण)

\Rightarrow  \angle DEC=35°

\triangle DCE में

\angle CDE+\angle DCE+\angle DEC=180° \\ \Rightarrow 53°+\angle DCE+35°=180° \\ \Rightarrow \angle DCE=180°-88° \\ \Rightarrow \angle DCE=92°
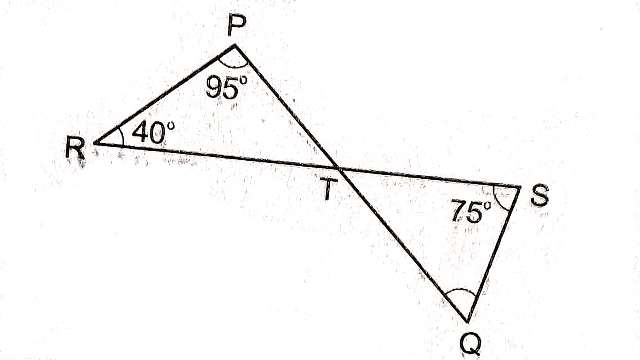
Example-6.चित्र में यदि रेखाएं PQ और RS बिन्दु T पर इस प्रकार प्रतिच्छेद करती है कि \angle PRT=40°,\angle RPT=95° और \angle TSQ=75° है तो \angle SQT ज्ञात कीजिए।
Solution–\triangle PRT में

\angle PRT + \angle RPT + \angle PTR=180° \\ \Rightarrow 40°+ 95°+\angle PTR=180° \\  \Rightarrow 135°+\angle PTR=180° \\ \Rightarrow \angle PTR=180°-135° \\  \Rightarrow \angle PTR=45° \\ \angle STQ=\angle PTR (शीर्षाभिमुख कोण)

\angle STQ=45°
\triangle STQ  में

\angle STQ +\angle TSQ+\angle SQT=180° \\ \Rightarrow 45°+ 75°+\angle SQT=180° \\ \Rightarrow 120°+\angle SQT=180° \\ \Rightarrow \angle SQT=180°-120° \\ \Rightarrow \angle SQT=60°
Example-7.चित्र में \triangle PQR की भुजाओं QP और RQ को क्रमशः बिन्दुओं S और T तक बढ़ाया गया है।यदि \angle SPR=135° है और \angle PQT=110° है तो \angle PRQ ज्ञात कीजिए।
Solution–\angle PQT + \angle PQR=180°(रैखिक कोण युग्म से)

\Rightarrow 110°+\angle PQR=180° \\ \Rightarrow \angle PQR=180°-110° \\ \Rightarrow \angle PQR=70° \\  \angle SPR+ \angle RPQ=180°(रैखिक कोण युग्म से)

\Rightarrow 135°+\angle RPQ=180° \\ \Rightarrow \angle RPQ=180°- 135°\\ \Rightarrow \angle RPQ=45°

\triangle PQR में 

\angle PRQ +\angle PQR+\angle RPQ=180° \\ \Rightarrow \angle PRQ +70°+45°=180° \\ \Rightarrow \angle PRQ +115°=180° \\ \Rightarrow \angle PRQ =180°-115° \\ \Rightarrow \angle PRQ =65°
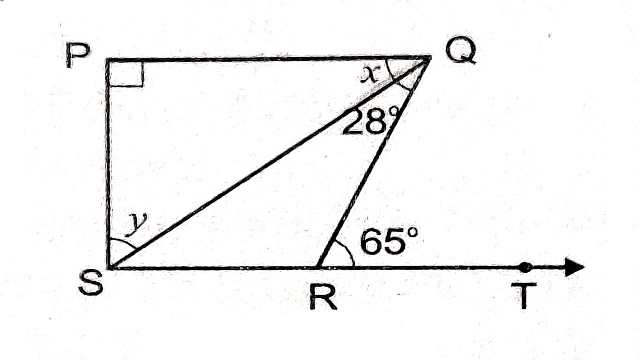
Example-8.चित्र में यदि  PQ \perp PS , PQ \parallel SR, \angle SQR=28° और \angle QRT=65°  है तो x और y के मान ज्ञात कीजिए।
Solution–\triangle QSR में

 \angle QSR +\angle SQR=\angle QRT \\ \Rightarrow  \angle QSR +28°=65° \\ \Rightarrow \angle QSR=65°-28° \\ \Rightarrow \angle QSR=37° \\ PQ \parallel SR
(बहिष्कोण=अन्तराभिमुख कोणों का योग)

अतः \angle PQS=\angle QSR(एकान्तर कोण)

\Rightarrow  \angle x=37°
\triangle PQS में

\angle P+\angle PQS+\angle PSQ=180° \\ \Rightarrow 90°+\angle x+\angle y=180° \\ \Rightarrow 90°+37°+\angle y=180° \\ \Rightarrow 127°+\angle y=180° \\ \Rightarrow \angle y=180° -127° \\ \Rightarrow \angle y=53° , \angle x=37°
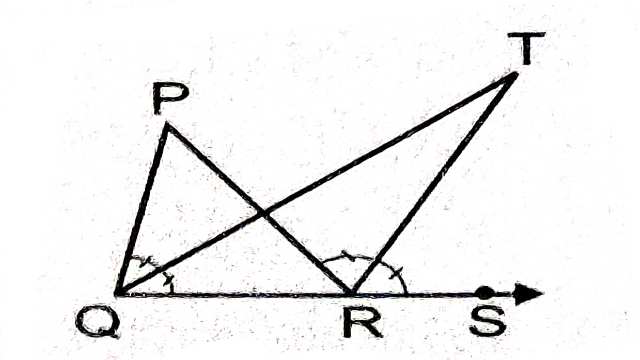
Example-9.चित्र में \triangle PQR की भुजा QR को बिन्दु S तक बढ़ाया गया है।यदि \angle PQR और \angle PRS के समद्विभाजक बिन्दु T पर मिलते हैं तो सिद्ध कीजिए कि \angle QTR=\frac{1}{2}  \angle QPR
Solution-दिया है (Given): \angle PQR और \angle PRS के समद्विभाजक क्रमशः QT व RT बिन्दु T पर मिलते हैं।

सिद्ध करना है (To Prove):\angle QTR=\frac{1}{2}  \angle QPR
उपपत्ति (Proof): \triangle QPR  में
\angle QPR+\angle PQR= \angle PRS (बहिष्कोण=अन्तराभिमुख कोणों का योग)
\angle PQR=2 \angle TQR (\because QT,\angle PQR का समद्विभाजक है)
\angle PRS=2 \angle TRS (\because TR, \angle PRS का समद्विभाजक है)
उपर्युक्त मान समीकरण (1) में रखने पर-

\angle QPR + 2 \angle TQR=2 \angle TRS \cdots(2)
\triangle TQR  में

\angle TRS=\angle TQR+\angle QTR \cdots(3)
(बहिष्कोण=अन्तराभिमुख कोणों का योग)
समीकरण (2) व (3) से-

\angle QPR + 2 \angle TQR=2 \left( \angle TQR +\angle QTR \right) \\ \Rightarrow \angle QPR + 2 \angle TQR=2  \angle TQR +2 \angle QTR \\ \Rightarrow \angle QPR =2 \angle QTR \\ \Rightarrow \angle QTR=\frac{1}{2} \angle QPR
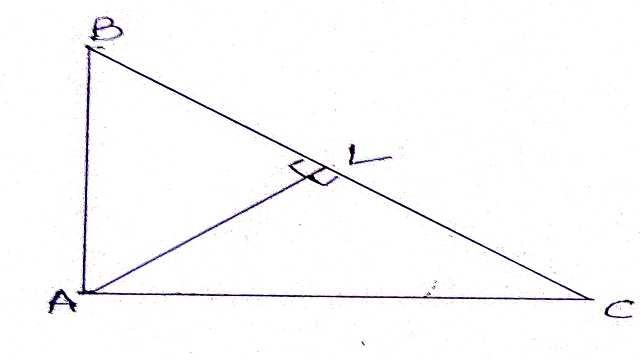
Example-10.एक त्रिभुज ABC का कोण A समकोण है।BC पर एक बिन्दु L इस प्रकार है किAL \perp BC है।सिद्ध कीजिए कि \angle BAL=\angle ACB
Solution-दिया है (Given):\triangle ABC समकोण त्रिभुज है तथा AL \perp BC

सिद्ध करना है (To Prove):\angle BAL=\angle ACB
उपपत्ति (Proof): \triangle BAC में \angle A=90°

\angle BAL+\angle CAL=90° \cdots(1)
\triangle ACL  में \angle ALC=90°

\angle CAL+\angle ACB=90° \cdots(2)
(1) व (2) से-

\angle BAL+\angle CAL=\angle CAL+\angle ACB \\ \Rightarrow \angle BAL=\angle ACB
उपर्युक्त उदाहरणों के द्वारा त्रिभुज के कोण क्या हैं? (What Are The Angles Of A Triangle?),त्रिभुज के गुणधर्म क्या हैं? (What Are The Properties of A Triangle?) को समझ सकते है

3.त्रिभुज के कोण क्या हैं की समस्याएं (What Are The Angles Of A Triangle Problems),त्रिभुज के गुणधर्म क्या हैं की समस्याएं (What Are The Properties of A Triangle Problems):

(1.) चित्र में त्रिभुज ABC का एक कोण 40° है।यदि शेष दोनों कोणों का अन्तर 30° हो तो उन्हें ज्ञात कीजिए।

(2.) चित्र में एवं \angle RPQ,\angle QRP ज्ञात \angle PQR कीजिए।

(3.) चित्र में \angle x,\angle y एवं \angle ACD ज्ञात कीजिए।यहां रेखा BA \parallel CE है।

(4.)यदि किसी त्रिभुज ABC के कोण B तथा C के समद्विभाजक बिन्दु O पर प्रतिच्छेद करते हैं तो सिद्ध कीजिए कि

\angle BOC=90°+\frac{\angle A}{2}

(5.)किसी त्रिभुज के कोणों का अनुपात 2:3:4 है।इस त्रिभुज के तीनों कोणों को ज्ञात कीजिए।
उत्तर (Answers):(1)\angle x=85°,\angle y=55° \\(2) \angle RPQ=63°,\angle PQR=63°,\angle QRP=54° \\(3)\angle x=42°,\angle ACD=108° ,\angle y=72°
(5.)40°,60°,80°
उपर्युक्त सवालों को हल करने पर त्रिभुज के कोण क्या हैं? (What Are The Angles Of A Triangle?),त्रिभुज के गुणधर्म क्या हैं? (What Are The Properties of A Triangle?)‌ को ठीक से समझ सकते हैं।

Also Read This Article:-Properties of Parallelograms Diagonals

4.त्रिभुज के कोण क्या हैं? (What Are The Angles Of A Triangle?),त्रिभुज के गुणधर्म क्या हैं? (What Are The Properties of A Triangle?) के बारे में अक्सर पूछे जाने वाले प्रश्न:

 

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Instagram	click here
4.	Linkedin	click here
5.	Facebook Page	click here