Volume of Combination of Solids
1.ठोसों के संयोजन का आयतन (Volume of Combination of Solids),ठोसों के संयोजन का आयतन कक्षा 10 (Volume of Combination of Solids Class 10):
ठोसों के संयोजन का आयतन (Volume of Combination of Solids) परिकलित करने की स्थिति में दो आधारभूत ठोसों के संयोजन से बने ठोस का आयतन वास्तव में दोनों घटकों के आयतनों के योग के बराबर होता है।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Areas of Combinations of Plane Figures
2.ठोसों के संयोजन का आयतन के उदाहरण (Volume of Combination of Solids Examples):
(जब तक अन्यथा न कहा जाए, \pi=\frac{22}{7} लीजिए)
Example:1.एक ठोस एक अर्द्धगोले पर खड़े एक शंकु के आकार का है जिनकी त्रिज्याएँ 1 cm हैं तथा शंकु की ऊँचाई उसकी त्रिज्या के बराबर है।इस ठोस का आयतन के पदों में ज्ञात कीजिए।
Solution:शंकु की त्रिज्या (r)=अर्द्धगोले की त्रिज्या (r)=1 cm
शंकु की ऊँचाई (h)=1 cm
शंकु का आयतन=\frac{1}{3} \pi r^2 h=\frac{1}{3} \pi(1)^2 \times 1 \\ =\frac{\pi}{3}
अर्द्धगोले का आयतन =\frac{2}{3} \pi r^3=\frac{2}{3} \pi(1)^3 \\ =\frac{2}{3} \pi
ठोस का आयतन=शंकु का आयतन+अर्द्धगोले का आयतन
=\frac{\pi}{3}+\frac{2}{3} \pi=\frac{\pi+2 \pi}{3}=\frac{3 \pi}{3}=\pi \\ =\pi घन सेमी
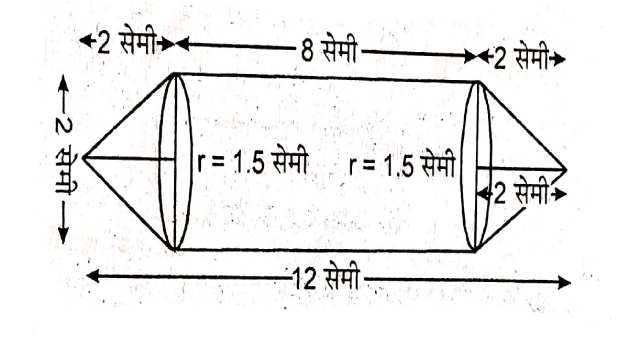
Example:2.एक इंजीनियरिंग के विद्यार्थी रचेल से एक पतली एल्युमीनियम की शीट का प्रयोग करते हुए एक माॅडल बनाने को कहा गया जो एक ऐसे बेलन के आकार का हो जिसके दोनों सिरों पर दो शंकु जुड़े हुए हों।इस माॅडल का व्यास 3 cm है।यदि प्रत्येक शंकु की ऊँचाई 2 cm हो तो रचेल द्वारा बनाए गए माॅडल में अन्तर्विष्ट हवा का आयतन ज्ञात कीजिए।
(यह मान लीजिए कि माॅडल की आंतरिक और बाहरी विमाएँ लगभग बराबर हैं।)
Solution:शंकु की त्रिज्या=बेलन की त्रिज्या=\frac{3}{2} सेमी
प्रत्येक शंकु की ऊँचाई (h_{1})=2 सेमी
बेलन की ऊँचाई (h_{2})=12-2-2=8 सेमी
दो शंकुओं का आयतन=2 \times \frac{1}{3} \pi r^2 h \\ =\frac{2}{3} \times \frac{22}{7} \times \frac{3}{2} \times \frac{3}{2} \times 2 \\=\frac{66}{7} घन सेमी
बेलन का आयतन=\pi r^2 h \\ =\frac{22}{7} \times \frac{3}{2} \times \frac{3}{2} \times 8=\frac{396}{7} घन सेमी
माॅडल में हवा का आयतन=दो शंकुओं का आयतन+बेलन का आयतन
=\frac{66}{7}+\frac{396}{7}=\frac{462}{7} \\ =66 घन सेमी
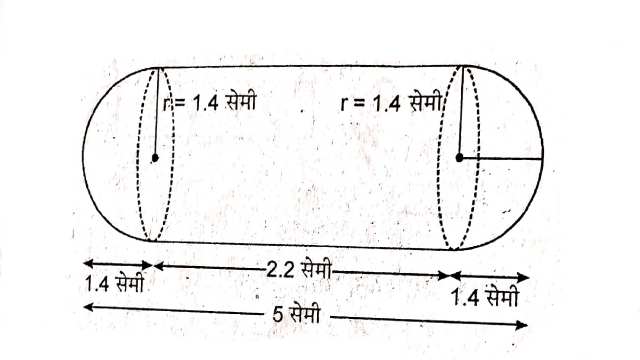
Example:3.एक गुलाबजामुन में उसके आयतन की लगभग 30% चीनी की चाशनी होती है। 45 गुलाबजामुनों में लगभग कितनी चाशनी होगी,यदि प्रत्येक गुलाबजामुन एक बेलन के आकार का है,जिसके दोनों सिरे अर्द्धगोलाकार हैं तथा इसकी लम्बाई 5 सेमी और व्यास 2.8 cm है (देखिए आकृति)।
Solution:बेलन की त्रिज्या=अर्द्धगोले की त्रिज्या (r)=\frac{2.8}{2}=1.4 सेमी
बेलनकार भाग की ऊँचाई (h)=5-1.4-1.4=2.2 सेमी
दो अर्द्धगोलों का आयतन=2 \times \frac{2}{3} \pi r^3 \\ =\frac{4}{3} \times \frac{22}{7} \times 1.4 \times 1.4 \times 1.4 \\ =\frac{34.496}{3} घन सेमी
बेलन का आयतन=\pi r^2 h \\ =\frac{22}{7} \times 1.4 \times 1.4 \times 2.2 \\ =13.552 घन सेमी
एक गुलाबजामुन का आयतन=\frac{34.496}{3}+13.552 \\ =\frac{40.656+34.496}{3} \\ =\frac{75.152}{3}
चीनी की चाशनी का आयतन=\frac{75.152}{3} \times \frac{30}{100} \\ 7.5152
45 गुलाबजामुनों में चाशनी का आयतन=7.5152×45=338.184 घन सेमी
\approx 338 घनसेमी
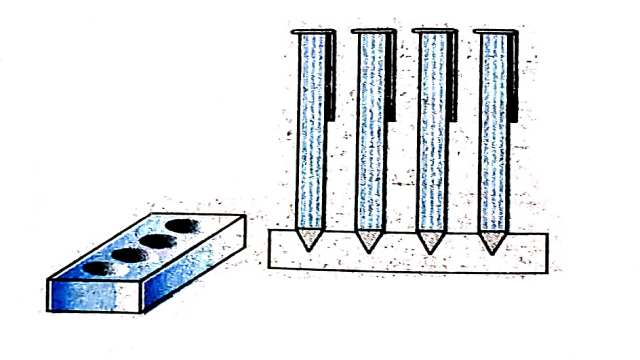
Example:4.एक कलमदान घनाभ के आकार की लकड़ी से बना है जिसमें कलम रखने के लिए चार शंक्वाकार गड्ढे बने हुए हैं।घनाभ की विमाएँ 15cm×10cm×3.5cm हैं।प्रत्येक गड्ढे की त्रिज्या 0.5 cm है और गहराई 1.4 cm है।पूरे कलमदान में लकड़ी का आयतन ज्ञात कीजिए (देखिए आकृति)।
Solution:घनाभ का आयतन=l×b×h
=15cm×10cm×3.5cm=525 घन सेमी
शंकु की त्रिज्या (r)=0.5 सेमी,शंकु की ऊँचाई=1.4 सेमी
4 शंक्वाकार गड्ढों का आयतन=4 \times \frac{1}{3} \pi r^2 h \\ =4 \times \frac{1}{3} \times \frac{22}{7} \times 0.5 \times 0.5 \times 1.4 \\ =\frac{4.4}{3}=1.467 घन सेमी
अतः कलमदान में लकड़ी का आयतन
=525-1.467
=523.533 घन सेमी
\approx 523.53 घन सेमी
Example:5.एक बर्तन एक उल्टे शंकु के आकार का है।इसकी ऊँचाई 8 cm है और इसके ऊपरी सिरे (जो खुला हुआ है) की त्रिज्या 5 cm है।यह ऊपर तक पानी से भरा हुआ है।जब इस बर्तन में सीसे की कुछ गोलियाँ जिनमें प्रत्येक 0.5 cm त्रिज्या वाला एक गोला है,डाली जाती हैं,तो इसमें भरे हुए पानी का एक चौथाई भाग बाहर निकल जाता है।बर्तन में डाली गई सीसे की गोलियों की संख्या ज्ञात कीजिए।
Solution:शंकु की त्रिज्या (r)=5 cm
शंकु की ऊँचाई (h)=8 cm
शंक्वाकार बर्तन में भरे जानेवाले पानी का आयतन=\frac{1}{3} \pi r^2 h\\=\frac{1}{3} \times \frac{22}{7} \times 5 \times 5 \times 8 \\ =\frac{4400}{21} घन सेमी
सीसे की गोलियाँ डालने से बाहर निकलने वाले पानी का आयतन=\frac{1}{4} \times \frac{4400}{21}=\frac{1100}{21}
सीसे की एक गोली का आयतन=\frac{4}{3} \pi r^3 \\ =\frac{4}{3} \times \frac{22}{7} \times 0.5 \times 0.5 \times 0.5 \\ =\frac{11}{21} घन सेमी
गोलियों की संख्या=\frac{\text{गोलियाँ डालने पर बाहर निकले पानी का आयतन}}{\text{एक गोली का आयतन}} \\=\frac{\frac{1100}{21}}{\frac{11}{21}}=\frac{1100}{21} \times \frac{21}{11}=100
Example:6.ऊँचाई 220 cm और आधार व्यास 24 cm वाले एक बेलन, जिस पर ऊँचाई 60 cm और त्रिज्या 8 cm वाला एक अन्य बेलन आरोपित है, से लोहे का एक स्तम्भ बना है।इस स्तम्भ का द्रव्यमान ज्ञात कीजिए,जबकि दिया है 1 घनसेमी लोहे का द्रव्यमान लगभग 8 g होता है। ( \pi=3.14लीजिए।)
Solution:बेलन की त्रिज्या r_{1}=12 सेमी
बेलन की ऊँचाई (h_{1})=220 सेमी
इस बेलन का आयतन=\pi r_{1}^2 h_{1}
=3.14×12×12×220
=99475.2 घनसेमी
दूसरे बेलन की त्रिज्या r_{2}=8 cm
दूसरे बेलन की ऊँचाई (h_{2})=60 cm
दूसरे बेलन का आयतन=\pi r_2^2 h_{2}
=3.14×8×8×60=12057.6 घनसेमी
पूरे स्तम्भ का आयतन=99475.2+12057.6
=111532.8 घनसेमी
बेलनकार स्तम्भ का द्रव्यमान=आयतन×1 घनसेमी लोहे का भार
=111532.8 \times \frac{8}{1000} किग्रा
=892.2624 \\ \approx 892.26 \mathrm{~kg}
Example:7.एक ठोस में, ऊँचाई 120 cm और त्रिज्या 60 cm वाला एक शंकु सम्मिलित है,जो 60 cm त्रिज्या वाले एक अर्द्धगोले पर आरोपित है।इस ठोस को पानी से भरे हुए एक लम्ब्वृत्तीय बेलन में इस प्रकार सीधा डाल दिया जाता है कि यह बेलन की तली को स्पर्श करे।यदि बेलन की त्रिज्या 60 cm है और ऊँचाई 180 cm है तो बेलन में शेष बचे पानी का आयतन ज्ञात कीजिए।
Solution:शंकु की त्रिज्या=अर्द्धगोले की त्रिज्या= बेलन की त्रिज्या (r)=60 सेमी
शंकु की ऊँचाई (h_{1})=120 सेमी
बेलन की ऊँचाई (h_{2})=180 सेमी
शंकु का आयतन=\frac{1}{3} \pi r^2 h \\ =\frac{1}{3} \times \frac{22}{7} \times 60 \times 60 \times 120=\frac{3168000}{7} घनसेमी
अर्द्धगोले का आयतन=\frac{2}{3} \pi r^3 \\ =\frac{2}{3} \times \frac{22}{7} \times 60 \times 60 \times 60=\frac{3168000}{7} घनसेमी
ठोस का आयतन=शंकु का आयतन+अर्द्धगोले का आयतन
=\frac{3168000}{7}+\frac{3168000}{7}=\frac{6336000}{7} \\ =\frac{6336000}{7} घनसेमी
बेलन का आयतन=\pi r^2 h \\ =\frac{22}{7} \times 60 \times 60 \times 180 \\ =\frac{14256000}{7} घनसेमी
बेलन में शेष बचे पानी का आयतन=बेलन का आयतन-ठोस का आयतन
=\frac{14256000}{7}-\frac{6336000}{7} \\ =\frac{7920000}{7}=1131428.571 घनसेमी
=\frac{1131428.571}{100 \times 100 \times 100}\\ =1.131428571 घनमीटर
\approx 1.131 घनमीटर
Example:8.एक गोलाकार काँच के बर्तन की एक बेलन के आकार की गर्दन है जिसकी लम्बाई 8cm है और व्यास 2 cm है जबकि गोलाकार भाग का व्यास 8.5 cm है।इसमें भरे जा सकने वाली पानी की मात्रा माप कर,एक बच्चे ने यह ज्ञात किया कि इस बर्तन का आयतन 345 घनसेमी है।जाँच कीजिए कि उस बच्चे का उत्तर सही है या नहीं, यह मानते हुए कि उपरोक्त मापन आंतरिक मापन है और \pi=3.14 ।
Solution:बेलनकार गर्दन की त्रिज्या (r)=\frac{2}{2}=1 सेमी
बेलनकार गर्दन की लम्बाई (h)=8 सेमी
गोलाकार भाग की त्रिज्या (R)=\frac{8.5}{2} सेमी
बेलनकार गर्दन का आयतन =\pi r^2 h=3.14 \times 1 \times 1 \times 8 =25.12 घनसेमी
गोलाकार भाग का आयतन =\frac{4}{3} \pi R^3=\frac{4}{3} \times 3.14 \times \frac{8.5}{2} \times \frac{8.5}{2} \times \frac{8.5}{2} \\ =\frac{964.17625}{3}=321.3920833 \\ \approx 321.392
बर्तन में पानी का आयतन=बेलनकार गर्दन में पानी का आयतन+गोले में पानी का आयतन
=25.12+321.392
=346.512 घनसेमी
अतः बच्चे का उत्तर 345 घनसेमी गलत है।बर्तन के पानी का सही आयतन 346.512 घनसेमी है।
उपर्युक्त उदाहरणों के द्वारा ठोसों के संयोजन का आयतन (Volume of Combination of Solids),ठोसों के संयोजन का आयतन कक्षा 10 (Volume of Combination of Solids Class 10) को समझ सकते हैं।
3.ठोसों के संयोजन का आयतन के सवाल (Volume of Combination of Solids Questions):
(1.)एक शंकु के आकार के बर्तन की त्रिज्या 10 सेमी और ऊँचाई 18 सेमी है,जो पानी से पूरा भरा हुआ है।इसे 5 सेमी त्रिज्या के एक बेलनकार बर्तन में उड़ेला जाता है।बेलनकार बर्तन में पानी की ऊँचाई ज्ञात कीजिए।
(2.)पानी से पूरी भरी हुई एक अर्द्धगोलाकार टंकी को एक पाइप द्वारा लीटर प्रति सेकण्ड की दर से खाली किया जाता है।यदि टंकी की त्रिज्या 1.5 मीटर है तो वह कितने समय में आधी खाली हो जाएगी?
उत्तर (Answers):(1.)पानी की ऊँचाई=24 सेमी (2.)16.5 मिनट
उपर्युक्त सवालों को हल करने पर ठोसों के संयोजन का आयतन (Volume of Combination of Solids),ठोसों के संयोजन का आयतन कक्षा 10 (Volume of Combination of Solids Class 10) को ठीक से समझ सकते हैं।
Also Read This Article:-Surface Area of Combination of Solids
4.ठोसों के संयोजन का आयतन (Frequently Asked Questions Related to Volume of Combination of Solids),ठोसों के संयोजन का आयतन कक्षा 10 (Volume of Combination of Solids Class 10) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.ठोस के आयतन की परिभाषा दीजिए। (Define Volume of a Solid):
उत्तर:प्रत्येक ठोस आकृति स्थान घेरती है।अतः ठोस आकृति द्वारा घेरे गए स्थान के माप को आयतन कहा जाता है।
प्रश्न:2.कुछ दैनिक जीवन में काम आनेवाले ठोसों के उदाहरण दीजिए। (Give Examples of Some Solids Used in Daily Life):
उत्तर:गोल खम्भे,गोल पाइप,आइस्क्रीम कोन,जोकर की टोपी,क्रिकेट की बाॅल,माचिस आदि बेलन,शंकु,गोले तथा घनाभ के उदाहरण हैं।
प्रश्न:3.विभिन्न ठोसों के आयतन के सूत्र लिखिए। (Write the Formulas for Volume of Different Solids):
उत्तर:(1.)घनाभ का आयतन=l×b×h
(2.)घन का आयतन=l^3
(3.)लम्ब्वृत्तीय बेलन का आयतन=\pi r^2 h
(4.)खोखले बेलन का आयतन=\pi\left(r_1^2-r_2^2\right) h
(5.)लम्ब्वृत्तीय शंकु का आयतन=\frac{1}{3} \pi r^2 h
(6.)गोले का आयतन=\frac{4}{3} \pi r^3
(7.)अर्द्धगोले का आयतन=\frac{2}{3} \pi r^3
(8.)गोलीय कोश का आयतन=\frac{4}{3} \pi\left(r_1^3-r_2^3\right)
जहाँ बाह्य त्रिज्या तथा अन्तःत्रिज्या है।
उपर्युक्त प्रश्नों के उत्तर द्वारा ठोसों के संयोजन का आयतन (Volume of Combination of Solids),ठोसों के संयोजन का आयतन कक्षा 10 (Volume of Combination of Solids Class 10) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Volume of Combination of Solids
ठोसों के संयोजन का आयतन
(Volume of Combination of Solids)
Volume of Combination of Solids
ठोसों के संयोजन का आयतन (Volume of Combination of Solids) परिकलित करने की
स्थिति में दो आधारभूत ठोसों के संयोजन से बने ठोस का आयतन वास्तव में दोनों घटकों के
आयतनों के योग के बराबर होता है।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.