Versions to Euclid 5th Postulate
1.यूक्लिड की पाँचवीं अभिधारणा का रूपान्तरण (Versions to Euclid 5th Postulate),यूक्लिड की पाँचवीं अभिधारणा के समतुल्य रूपान्तरण (Conversion Equivalent to Euclid’s Fifth Postulate):
यूक्लिड की पाँचवीं अभिधारणा का रूपान्तरण (Versions to Euclid 5th Postulate) के अनेक समतुल्य रूपान्तरण हैं।इनमें से एक प्लेफेयर का अभिगृहीत भी है।इस आर्टिकल में प्लेफेयर के अभिगृहीत बारे में बताया गया है।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Euclid Geometry Class 9
2.यूक्लिड की पाँचवीं अभिधारणा के समतुल्य रूपान्तरण (Conversion Equivalent to Euclid’s Fifth Postulate):
गणित के इतिहास में यूक्लिड की पाँचवीं अभिधारणा का अत्यधिक महत्व है।इस अभिधारणा के परिणामस्वरूप यदि दो रेखाओं पर गिरने वाली रेखा के एक ही ओर के दोनों अंतःकोणों का योग 180° हो तो दोनों रेखाएँ कभी प्रतिच्छेद नहीं कर सकतीं।इस अभिधारणा के अनेक समतुल्य रूपान्तरण (equivalent versions) हैं।इनमें से एक प्लेफेयर का अभिगृहीत (playfair’ Axiom) है (जिसे स्काॅटलैण्ड के एक गणितज्ञ जाॅन प्लेफेयर ने 1729 में दिया था)।यह इस प्रकार हैः
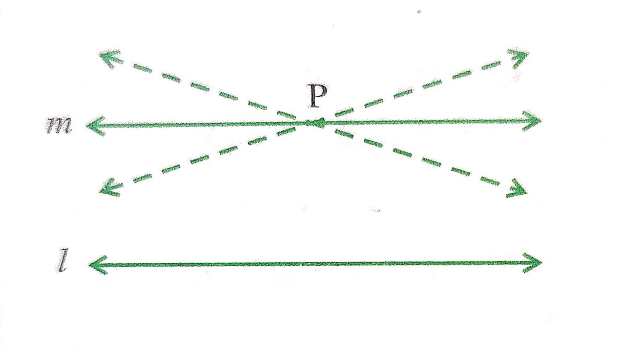
प्रत्येक रेखा l और उस पर न स्थित बिन्दु P के लिए,एक अद्वितीय रेखा m ऐसी होती है जो P से होकर जाती है और l के समान्तर है।
आकृति में आप देख सकते हैं कि P से होकर जाने वाली सभी रेखाओं में से केवल m ही रेखा l के समान्तर है।
इस परिणाम को निम्नलिखित रूप में भी व्यक्त किया जा सकता हैः
दो भिन्न प्रतिच्छेदी रेखाएँ एक ही रेखा के समान्तर नहीं हो सकतीं।
3.अयूक्लिडीय ज्यामिति (Non-Euclidean Geometries):
- यूक्लिड को अपनी 28 प्रमेयों को सिद्ध करने में पाँचवीं अभिधारणा की कोई आवश्यकता नहीं पड़ी। अनेक गणितज्ञों और स्वयं यूक्लिड को यह विश्वास था कि पाँचवीं अभिधारणा वास्तव में एक प्रमेय है,जिसे चारों अभिधारणाओं और अन्य अभिगृहीतों की सहायता से सिद्ध किया जा सकता है।परन्तु पाँचवीं अभिधारणा को प्रमेय के रूप में सिद्ध करने के सभी प्रयत्न असफल रहे।
- परन्तु इन प्रयत्नों के कारण एक महत्त्वपूर्ण उपलब्धि हुई – यह उपलब्धि अनेक अन्य ज्यामितियों की रचनाएँ (सृष्टि) रही।ये ज्यामितियाँ यूक्लिडीय ज्यामिति (Euclidean Geometry) से बहुत भिन्न हैं।इन्हें अयूक्लिडीय ज्यामितियाँ (Non-Euclidean Geometries) कहा जाता है।
- इन ज्यामितियों की रचना को विचारों के इतिहास में एक मील का पत्थर माना जाता है क्योंकि तब तक प्रत्येक व्यक्ति यह विश्वास करता था कि यूक्लिड की ज्यामिति ही एकमात्र ज्यामिति है और सम्पूर्ण विश्व यूक्लिडीय है।जिस विश्व में हम रह रहे हैं,उसकी ज्यामिति को अब अयूक्लिडीय ज्यामिति दर्शाया जा चुका है।वास्तव में यह गोलाकार ज्यामिति (spherical geometry) कहलाती है।
- गोलाकार ज्यामिति में रेखाएँ सीधी रेखाएँ नहीं होती हैं।ये रेखाएँ दीर्घवृत्तों (great circles) (जो एक गोले और उसके केन्द्र से होकर जाने वाले तलों के प्रतिच्छेदन से प्राप्त वृत्त होते हैं) के भाग होती हैं।
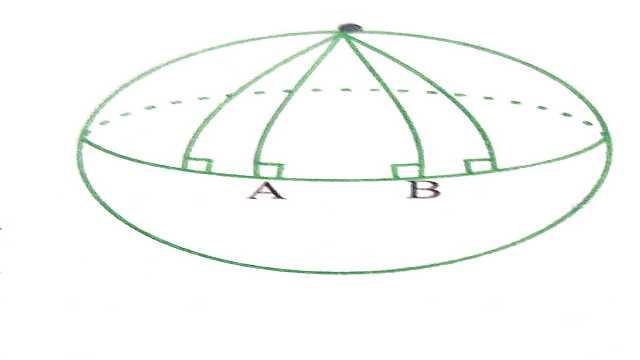
- आकृति में रेखाएँ AN और BN (जो एक गोले के दीर्घवृत्तों के भाग हैं) एक ही रेखा AB पर लम्ब हैं।परन्तु ये एक दूसरे से मिल रही है यद्यपि रेखा AB के एक ही ओर के अंतः कोणों का योग दो समकोणों से कम नहीं है (वास्तव में यह 90°+90°=180° है)।
- साथ ही ध्यान दीजिए कि त्रिभुज NAB के कोणों का योग 180° से अधिक है क्योंकि \angle A+\angle B=180° है।इस प्रकार यूक्लिडीय ज्यामिति केवल एक तल में बनी आकृतियों के लिए ही मान्य है।वक्र पृष्ठों में यह असफल रहती है।
4.यूक्लिड की पाँचवीं अभिधारणा का रूपान्तरण के साधित उदाहरण (Versions to Euclid 5th Postulate Solved Examples):
Example:1.आप यूक्लिड की पाँचवीं अभिधारणा को किस प्रकार लिखेंगे ताकि वह सरलता से समझी जा सके?
Solution:यूक्लिड की अभिधारणा पाँच के अनेक समतुल्य रूपान्तरण हैं।इनमें से एक प्लेफेयर का अभिगृहीत है जो कि सरलता से समझा जा सकता है।इसके अनुसारः
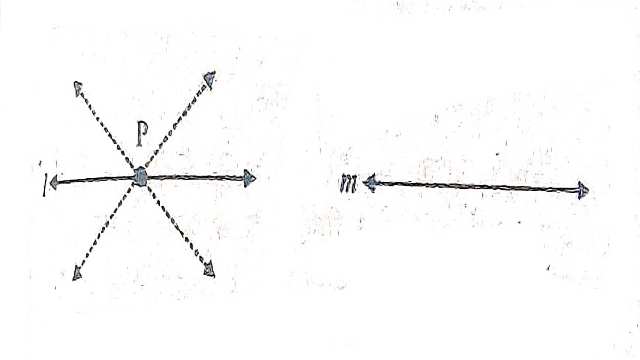
प्रत्येक रेखा l और उस पर न स्थित बिन्दु P के लिए,एक अद्वितीय रेखा m ऐसी होती है जो P से होकर जाती है और l के समान्तर है।
स्पष्टतः P से होकर जानेवाली सभी रेखाओं में केवल m ही रेखा l के समान्तर है।
Example:2.क्या यूक्लिड की पाँचवीं अभिधारणा से समान्तर रेखाओं के अस्तित्व का औचित्य निर्धारित होता है? स्पष्ट कीजिए।
Solution:हाँ,यूक्लिड की पाँचवीं अभिधारणा समान्तर रेखाओं के अस्तित्व का औचित्य निर्धारित करती है क्योंकि यदि कोई रेखा l दो सरल रेखाओं m और n पर पड़ती हो कि l की एक ओर के अंतःकोणों का योग दो समकोण (180°) हो तो यूक्लिड के पाँचवें अभिगृहीत के अनुसार यह रेखा l के इस ओर नहीं मिलेगी।
अब हम जानते हैं कि रेखा l की दूसरी ओर अंतःकोणों का योग भी दो समकोण होगा।अतः दूसरी ओर भी ये नहीं मिलेंगे।अतः रेखाएँ m और n कभी भी नहीं मिलेंगे और इसलिए ये समान्तर हैं।
उपर्युक्त उदाहरणों के द्वारा यूक्लिड की पाँचवीं अभिधारणा का रूपान्तरण (Versions to Euclid 5th Postulate),यूक्लिड की पाँचवीं अभिधारणा के समतुल्य रूपान्तरण (Conversion Equivalent to Euclid’s Fifth Postulate) को समझ सकते हैं।
Also Read This Article:-Mean Median and Mode Class 9
5.यूक्लिड की पाँचवीं अभिधारणा का रूपान्तरण से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न (Frequently Asked Questions Related to Versions to Euclid 5th Postulate),यूक्लिड की पाँचवीं अभिधारणा के समतुल्य रूपान्तरण (Conversion Equivalent to Euclid’s Fifth Postulate):
प्रश्न:1.ज्यामिति किसे कहते हैं? (What is Geometry?):
उत्तरःगणित की जिस शाखा के अन्तर्गत बिन्दुओं,रेखाओं,तलों और ठोस पिण्डों के आकार,विस्तार और गुणों का अध्ययन किया जाता है,उसे ज्यामिति कहते हैं।
प्रश्न:2.रेखा किसे कहते हैं? (What is a Line Called?):
उत्तरःरेखा वह ज्यामितीय आकृति होती है जिसकी कोई मोटाई नहीं होती है,इसकी लम्बाई असीमित होती है अर्थात् दोनों ओर अनन्त तक बढ़ी हुई होती है।
प्रश्न:3.रेखाखण्ड किसे कहते हैं? (What is Segment?) :
उत्तर:रेखा का वह भाग जिसकी एक निश्चित लम्बाई होती है और दो अन्त्य बिन्दु होते हैं।रेखाखण्ड कहलाता है।
प्रश्न:4.संरेखीय बिन्दु किसे कहते हैं? (What are the Collinear points Called?):
उत्तरःवे बिन्दु जो एक सरल रेखा पर स्थित होते हैं संरेखीय बिन्दु कहलाते हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा यूक्लिड की पाँचवीं अभिधारणा का रूपान्तरण (Versions to Euclid 5th Postulate),यूक्लिड की पाँचवीं अभिधारणा के समतुल्य रूपान्तरण (Conversion Equivalent to Euclid’s Fifth Postulate) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Versions to Euclid’s 5th Postulate
यूक्लिड की पाँचवीं अभिधारणा का रूपान्तरण
(Versions to Euclid’s 5th Postulate)
Versions to Euclid’s 5th Postulate
यूक्लिड की पाँचवीं अभिधारणा का रूपान्तरण (Versions to Euclid’s 5th Postulate)
के अनेक समतुल्य रूपान्तरण हैं।इनमें से एक प्लेफेयर का अभिगृहीत भी है।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.