Trigonometrical Identities Class 10
1.त्रिकोणमितीय सर्वसमिकाएं कक्षा 10 (Trigonometrical Identities Class 10),त्रिकोणमितीय सर्वसमिकाएं (Trigonometric Identities):
त्रिकोणमितीय सर्वसमिकाएं कक्षा 10 (Trigonometrical Identities Class 10) को समझने से पूर्व सर्वसमिका को समझना होगा।एक समीकरण को एक सर्वसमिका तब कहा जाता है जबकि यह सम्बन्धित चरों के सभी मानों के लिए सत्य हो।इसी प्रकार एक कोण के त्रिकोणमितीय अनुपातों से सम्बन्धित सर्वसमिका को त्रिकोणमितीय सर्वसमिका कहा जाता है जबकि यह सम्बन्धित कोण (कोणों) के सभी मानों के लिए सत्य होता है।
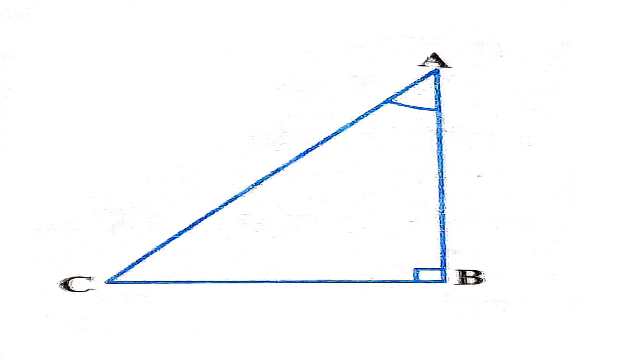
\triangle ABC में,जो B पर समकोण है (देखिए आकृति)
हमें यह प्राप्त होता है AB^2+BC^2=AC^2 \cdots(1)
(1) के प्रत्येक पद को से भाग देने पर हमें यह प्राप्त होता है
\frac{A B^2}{A C^2}+\frac{B C^2}{A C^2}=\frac{A C^2}{A C^2} \\ \Rightarrow\left(\frac{A B}{A C}\right)^2+\left(\frac{B C}{A C}\right)^2=\left(\frac{A C}{(A C}\right)^2 \\ \Rightarrow \cos ^2 A+\sin ^2 A=1 \quad \cdots(2)
यदि सभी A के लिए, जहाँ 0 \leq A \leq 90^{\circ} सत्य होता है।अतः यह एक त्रिकोणमितीय सर्वसमिका है।
अब हम (1) को AB^2 से भाग दें।ऐसा करने पर हमें यह प्राप्त होता है
\frac{A B^2}{A B^2}+\frac{B C^2}{A B^2}=\frac{A C^2}{A B^2} \\ \Rightarrow \left(\frac{A B}{A B}\right)^2+\left(\frac{B C}{A B}\right)^2=\left(\frac{A C}{A B}\right)^2 \\ \Rightarrow 1+\tan^2 A=\sec ^2 A \cdots(3)
यह समीकरण A=0° के लिए सत्य है परन्तु A=90° के लिए सत्य नहीं है।A=90° के लिए tan A और sec A परिभाषित नहीं है।अतः (3),ऐसे सभी A के लिए सत्य होता है जहाँ 0 \leq A \leq 90^{\circ}
अब (1) को BC^2 से भाग देने पर हमें प्राप्त होता हैः
\frac{A B^2}{B C^2}+\frac{B C^2}{B C^2}=\frac{A C^2}{A C^2} \\ \Rightarrow \left(\frac{A B}{B C}\right)^2+\left(\frac{B C}{B C}\right)^2=\left(\frac{A C}{B C}\right)^2 \\ \Rightarrow \cot ^2 A+1=\operatorname{cosec}^2 A \cdots(4)
A=0° के लिए cosec A और cot A परिभाषित नहीं है।अतः ऐसे सभी A के लिए (4) सत्य होता है जहाँ 0 \leq A \leq 90^{\circ}
इन सर्वसमिकाओं का प्रयोग करके हम प्रत्येक त्रिकोणमितीय अनुपात को अन्य त्रिकोणमितीय अनुपातों के पदों में व्यक्त कर सकते हैं अर्थात् यदि कोई एक अनुपात ज्ञात हो तो हम अन्य त्रिकोणमितीय अनुपातों के मान ज्ञात कर सकते हैं।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Complementary Angles Class 10
2.त्रिकोणमितीय सर्वसमिकाएं कक्षा 10 पर आधारित उदाहरण (Examples Based on Trigonometrical Identities Class 10):
Example:1.त्रिकोणमितीय अनुपातों Sin A,sec A और tan A को cot A के पदों में व्यक्त कीजिए।
Solution: \sin A=\frac{1}{\operatorname{cosec} A} \\ \Rightarrow \sin A =\frac{1}{\sqrt{1+\cot ^2 A}}\left[1+\cot ^2 A=\operatorname{cosec}^2 A\right] \\ \sec ^2 A =1+\tan ^2 A \\ =1+\frac{1}{\cot ^2 A} \\ =\frac{1+\cot ^2 A}{\cot ^2 A} \\ \Rightarrow \sec A =\frac{\sqrt{1+\cot ^2 A}}{\cot A} \\ \tan A =\frac{1}{\cot ^2 A}
Example:2.\angle A के अन्य सभी त्रिकोणमितीय अनुपातों को sec A के पदों में लिखिए।
Solution:- \text{(i)} \sin ^2 A+\cos ^2 A=1 \\ \Rightarrow \sin ^2 A=1-\cos ^2 A \\ \Rightarrow \sin^2 A=1-\frac{1}{\sec^2 A} \\ \Rightarrow \sin ^2 A=\frac{\sec ^2 A-1}{\sec ^2 A} \\ \Rightarrow \sin A=\frac{\sqrt{\sec ^2 A-1}}{\sec A} \\ \text{(ii)} \cos A=\frac{1}{\sec A} \\ \text { (iii) } 1+t \cos ^2 A=\sec ^2 A \\ \Rightarrow \tan ^2 A=\sec ^2 A-1 \\ \Rightarrow \tan A=\sqrt{\sec ^2 A-1} \\ \text { (iv) } \operatorname{cosec} A=\frac{1}{\sin A} \\ \Rightarrow \operatorname{cosec} A=\frac{1}{\frac{\sqrt{\sec ^2 A-1}}{\sec A}} \\ \Rightarrow \operatorname{cosec} A=\frac{\sec A}{\sqrt{\sec ^2 A-1}} \\ \text { (v) } \cot A=\frac{1}{\tan A} \\ \Rightarrow \cot A=\frac{1}{\sqrt{\sec ^2 A-1}}
Example:3.मान निकालिएः
Example:3(i). \frac{\sin ^2 63^{\circ}+\sin ^2 27^{\circ}}{\cos ^2 17^{\circ}+\cos ^2 73^{\circ}}
Solution: \frac{\sin ^2 63^{\circ}+\sin ^2 27^{\circ}}{\cos ^2 17^{\circ}+\cos ^2 73^{\circ}} \\ =\frac{\sin ^2 63^{\circ}+\sin ^2\left(90^{\circ}-63^{\circ}\right)}{\cos ^2\left(90^{\circ} 73^{\circ}\right)+\cos ^2 73^{\circ}} \\ =\frac{\sin ^2 63^{\circ}+\cos ^2 63^{\circ}}{\sin ^2 73^{\circ}+\cos ^2 73^{\circ}} \\ =\frac{1}{1} \quad\left(\sin ^2 \theta+\cos ^2 \theta=1\right) \\ =1
Example:3(ii). \sin 25^{\circ} \cos 65^{\circ}+\cos 25^{\circ} \sin 65^{\circ}
Solution: \sin 25^{\circ} \cos 65^{\circ}+\cos 25^{\circ} \sin 65^{\circ} \\ \Rightarrow \sin 25^{\circ} \cos \left(90^{\circ}-25^{\circ}\right)+\cos 25^{\circ} \sin \left(90^{\circ}-25^{\circ}\right) \\ \Rightarrow \sin 25^{\circ} \sin 25^{\circ}+\cos 25^{\circ} \cos 25^{\circ} \\ \Rightarrow \sin ^2 25^{\circ}+\cos ^2 25^{\circ} \\ =1 \quad\left(\sin ^2 \theta+\cos ^2 \theta=1\right)
Example:4.सही विकल्प चुनिए और अपने विकल्प की पुष्टि कीजिएः
Example:4(i). 9 \sec ^2 A-9 \tan^{2} A
(A)1 (B)9 (C)8 (D)0
Solution: 9 \sec ^2 A-9 \tan ^2 A \\ =9\left(\sec ^2-\tan ^2 A\right) \\ =9(1) \quad\left(\sec ^2 A-\tan ^2 A=1\right) \\ =9
Example:4(ii). (1+\tan \theta+\sec \theta)(1+\cot \theta-\operatorname{cosec} \theta) बराबर हैः
(A) 0 (B) 1 (C) 2 (D) – 1
Solution: (1+\tan \theta+\sec \theta)(1+\cot \theta-\operatorname{cosec} \theta) \\ =1+\cot \theta-\operatorname{cosec} \theta+\tan \theta+\tan \theta-\cot \theta- \tan \theta \operatorname{cosec} \theta+\sec \theta+\sec \theta \cdot \cot \theta-\sec \theta \operatorname{cosec} \theta \\ =1+\frac{\cos \theta}{\sin \theta}-\frac{1}{\sin \theta}+\frac{\sin \theta}{\cos \theta}+1-\frac{\sin \theta}{\cos \theta} \cdot \frac{1}{\sin \theta}+\frac{1}{\cos \theta} +\frac{1}{\cos \theta}-\frac{\cos \theta}{\sin \theta}-\frac{1}{\cos \theta} \cdot \frac{1}{\sin \theta} \\ =\frac{\sin \theta \cos \theta+\cos ^2 \theta-\cos \theta+\sin ^2 \theta+\sin \theta \cos \theta-\sin \theta+\sin \theta +\cos \theta -1}{\cos \theta \sin \theta} \\ =\frac{2 \cos \theta-1}{\cos \theta \cos \theta} \\ =\frac{2 \sin \theta \cos \theta}{\cos \theta \sin \theta} \\ =2
(c) 2 Ans
Example:4(iii). (\sec A+\tan A)(1-\sin A) बराबर हैः
(A)sec A (B)sin A (C)cosec A (D) cos A
Solution: (\sec A+\tan A)(1-\sin A) \\ =\left(\frac{1}{\cos A}+\frac{\sin A}{\cos A}\right)(1-\sin A) \\ =\frac{(1+\sin A)}{\cos A}(1-\sin A) \\ =\frac{1-\sin ^2 A}{\cos ^2 A} \\ =\frac{\cos ^2 A}{\cos A} \\ =\cos A
(D) \cos A Ans
Example:4(iv). \frac{1+\tan ^2 A}{1+\cot ^2 A} बराबर हैः
(A) \sec ^2 A (B) -1 (C) \cot^{2} A (D)\tan ^2 A
Solution: \frac{1+\tan ^2 A}{1+\cot ^2 A} \\ \frac{\sec ^2 A}{\operatorname{cosec}^2 A}=\frac{1}{\cos ^2 A} \times \frac{\sin ^2 A}{1}=\tan ^2 A
(D) \tan ^2 A Ans.
Example:5.निम्न सर्वसमिकाएं सिद्ध कीजिए,जहाँ वे कोण,जिनके लिए व्यंजक परिभाषित है,न्यून कोण हैः
Example:5(i). (\operatorname{cosec} \theta-\cot \theta)^2=\frac{1-\cos \theta}{1+\cos \theta}
Solution: (\operatorname{cosec} \theta-\cot \theta)^2=\frac{1-\cos \theta}{1+\cos \theta} \\ \text { L.H.S. } (\operatorname{cosec} \theta-\cot \theta)^2 \\ \Rightarrow \left(\frac{1}{\sin \theta}-\frac{\cos \theta}{\sin \theta}\right)^2 \\ = \left(\frac{1-\cos \theta}{\sin \theta}\right)^2 \\ = \frac{(1-\cos \theta)^2}{\sin \theta} \\ = \frac{(1-\cos \theta)^2}{1-\cos ^2 \theta} \\ = \frac{(1-\cos \theta)^2}{(1-\cos \theta)(+\cos \theta)} \\ = \frac{1-\cos \theta}{1+\cos \theta}=\text { R.H.S. }
Example:5(ii). \frac{\cos A}{1+\sin A}+\frac{1+\sin A}{\cos A}=2 \sec A
Solution: \frac{\cos A}{1+\sin A}+\frac{1+\sin A}{\cos A}=2 \sec A \\ \text { L.H.S } =\frac{\cos A}{1+\sin A}+\frac{1+\sin A}{\cos A} \\=\frac{\cos ^2 A+(1+\sin A)^2}{\cos ^2 A(1+\sin A)} \\ = \frac{\cos ^2 A+1+\sin ^2 A+2 \sin A}{\cos ^2 A(1+\sin A)} \\ = \frac{1+1+2 \sin A}{\cos A(1+\sin A)} \\ = \frac{2+2 \sin A}{\cos A(1+\sin A)} \\ = \frac{2(1+\sin A)}{\cos A(1+\sin A)} \\ = \frac{2}{\cos A} \\ = 2 \sec A=\text { R.H.S }
Example:5(iii). \frac{\tan \theta}{1-\cot \theta}+\frac{\cot \theta}{1-\tan \theta}=1+\sec \theta \operatorname{cosec} \theta
Solution: \frac{\tan \theta}{1-\cot \theta}+\frac{\cot \theta}{1-\tan \theta}=1+\sec \theta \operatorname{cosec} \theta \\ \text { L.H.S. } \frac{\tan \theta}{1-\cot \theta}+\frac{\cot \theta}{1-\tan \theta} \\ \frac{\tan \theta}{1-\frac{1}{\tan \theta}}+\frac{\frac{1}{\tan \theta}}{1-\tan \theta} \\ =\frac{\tan ^2 \theta}{\tan \theta-1}+\frac{1}{\tan \theta(1-\tan \theta)} \\ =-\frac{\tan ^2 \theta}{1-\tan \theta}+ \frac{1}{\tan \theta(1-\tan \theta)} \\ =\frac{-\tan ^3 \theta+1}{\tan ^3 \theta(1-\tan \theta)} \\ =\frac{(1-\tan \theta)}{\tan \theta(1-\tan \theta)} \\ =\frac{(1-\tan \theta)\left(1+\tan ^2 \theta+\tan \theta\right)}{\tan \theta(1-\tan \theta)} \\ =\frac{1+\tan ^2 \theta+\tan \theta}{\tan \theta} \\ =\frac{\sec ^2 \theta+ \tan \theta}{\tan \theta} \\ =\frac{\sec ^2 \theta+\tan \theta}{\tan \theta} \\ =\frac{\sec ^2 \theta}{\tan \theta}+1 \\ =\frac{\frac{1}{\cos ^2 \theta}}{\frac{\sin \theta}{\cos \theta}}+1 \\=\frac{1}{\cos ^2 \theta} \cdot \frac{\cos \theta}{\sin \theta}+1 \\=1+\frac{1}{\sin \theta \cos \theta} \\ =1+\operatorname{cosec} \theta \sec \theta=\text { R.H.S. }
Example:5(iv). \frac{1+\sec A}{\sec A}=\frac{\sin ^2 A}{1-\cos A}
Solution: \frac{1+\sec A}{\sec A}=\frac{\sin ^2 A}{1-\cos A} \\ \text{L.H.S.}= \frac{1+\sec A}{\sec A} \\=\frac{1+\frac{1}{\cos A}}{\frac{1}{\cos A}} \\ =\frac{\frac{1+\cos A}{\cos A}}{\frac{1}{\cos A}} \\ =1+\cos A \\ =(1+\cos A) \frac{(1-\cos A)}{(1-\cos A)} \\ =\frac{1-\cos ^2 A}{1-\cos A} \\ =\frac{\sin^2 A}{1-\cos A}=\text{R.H.S.}
Example:5(v). सर्वसमिका \operatorname{cosec}^2 A=1+\cos ^2 A लागू करने पर \frac{\cos A -\sin A+1}{\cos A+\sin A-1}=\operatorname{cosec} A+\cot A
Solution: \frac{\cos A-\sin A+1}{\cos A+\sin A-1}=\operatorname{cosec} A+\cot A \\ \text{L.H.S.}= \frac{\cos A-\sin A+1}{\cos A+\sin A-1}
अंश व हर में sin A का भाग देने परः
\frac{\frac{\cos A}{\sin A}-\frac{\sin A}{\sin A}+\frac{1}{\sin A}}{\frac{\cos A}{\sin A}+\frac{\sin A}{\sin A}-\frac{1}{\sin A}} \\ =\frac{\cot A-1+\operatorname{cosec} A}{\cot A+1-\operatorname{cosec} A} \\ = \frac{\operatorname{cosec} A+\cot A-\left(\operatorname{cosec}^{2} A-\cot ^2 A\right)}{\cot A+1-\operatorname{cosec} A} \\ =\frac{\operatorname{cosec} A+\cot A-(\operatorname{cosec} A+\cot A)(\operatorname{cosec} A-\cot A)}{\cot A+1-\operatorname{cosec} A} \\ =\frac{(\operatorname{cosec} A+\cot A)(1-\operatorname{cosec} A+\cot A)}{\cot A+1-\operatorname{cosec} A} \\ =\operatorname{cosec} A+\cot A=\text{R.H.S.}
Example:5(vi). \sqrt{\frac{1+\sin A}{1-\sin A}}=\sec A+\tan A
Solution: \sqrt{\frac{1+\sin A}{1-\sin A}}=\sec A+\tan A \\ \text{L.H.S.}= \sqrt{\frac{1+\sin A}{1-\sin A}} \\ =\sqrt{\frac{1+\sin A}{1-\sin A} \times \frac{1+\sin A}{1+\sin A}} \\ =\sqrt{\frac{(1+\sin A)^2}{1-\sin ^2 A}} \\ =\frac{1+\sin A}{\sqrt{\cos ^2 A}} \\ =\frac{1+\sin A}{\cos A} \\ =\frac{1}{\cos A}+\frac{\sin A}{\cos A} \\ =\sec A+\tan A=\text { R.H.S. }
Example:5(vii). \frac{\sin \theta-2 \sin \theta}{2 \cos ^3 \theta-\cos \theta}=\tan \theta
Solution: \frac{\sin \theta-2 \sin \theta \theta}{2 \cos ^3 \theta-\cos \theta}=\tan \theta \\ \text { L.H.S. }=\frac{\sin \theta-2 \sin ^3 \theta}{2 \cos ^3 \theta-\cos \theta} \\ \frac{\sin \theta\left(1-2 \sin ^2 \theta \right)}{\cos \theta\left(2 \cos ^2 \theta-1\right)} \\ =\frac{\tan \theta\left(1-2 \sin ^2 \theta\right)}{2\left(1-\sin ^2 \theta\right)-1} \\ =\frac{\tan \theta\left(1-2 \sin ^2 \theta\right)}{2-2 \sin ^2 \theta-1} \\ =\frac{\tan \theta\left(1-2 \sin ^2 \theta\right)}{\left(1-2 \sin ^2 \theta\right)} \\ = \tan \theta=\text { R.H.S. }
Example:5(viii). (\sin A + cosec A)^2+ (\cos A+\sec A)^2=7+\tan ^2 A+\cot ^2 A
Solution: (\sin A+\operatorname{cosec} A)^2+(\cos A+\sec A)^2 =7+\tan ^2 A+\cot ^2 A \\ \text { L.H.S }(\sin A+\operatorname{cosec} A)^2+(\cos A+\sec A)^2 \\ =\sin ^2 A+\operatorname{cosec}^2 A+2 \sin A \operatorname{cosec} A+\cos ^2 A+\sec ^2 A+2 \cos A \sec A \\ =\sin ^2 A+\cos ^2 A+1+\cot ^2 A+2+ 1+\tan ^2 A+2 \\ \left[\because \operatorname{cosec}^2 A=1+\cot ^2 A, \sec ^2 A=1+\tan ^2 A\right] \\ =1+6+\tan ^2 A+\cot ^2 A \\ =7+\tan ^2 A+\cot ^2 A=\text { R.H.S }
Example:5(ix). (\operatorname{cosec} A-\sin A)(\sec A-\cos A)=\frac{1}{\tan A+\cot A}
Solution:(\operatorname{cosec} A-\sin A)(\operatorname{cec} A-\cos A) =\frac{1}{a \tan A+\cos A} \\ \text{L.H.S.}=(\operatorname{cosec} A-\sin A)(\sec A-\cos A) \\ \left(\frac{1}{\sin A}-\sin A\right) \left(\frac{1}{\cos A}-\cos A\right) \\ =\left(\frac{1-\sin ^2 A}{\sin A}\right)\left(\frac{1-\cos ^2 A}{\cos A}\right) \\ =\frac{\cos ^2 A}{\sin A} \cdot \frac{\sin ^2 A}{\cos A} \\ =\frac{\sin A \cos A}{1} \\ =\frac{\sin A \cos A}{\sin ^2 A+\cos ^2 A} \\ =\frac{1}{\frac{\sin ^2 A}{\sin A \cos A}+\frac{\cos ^2 A}{\sin A \cos A}} \\ =\frac{1}{\frac{\sin A}{\cos A}+\frac{\cos A}{\sin A}} \\ =\frac{1}{\tan A+\cot A}=\text { R.H.S. }
Example:5(x). \left(\frac{1+\tan ^2 A}{1+\cot ^2 A}\right)=\left(\frac{1-\tan A}{1-\cot A}\right)^2=\tan ^2 A
Solution: 2\left(\frac{1+\tan ^2 A}{1+\cot ^2 A}\right)=\left(\frac{1-\tan A}{1-\cot A}\right)^2=\tan ^2 A \\ \text { L.H.S }=\frac{1+\tan ^2 A}{1+\cos ^2 A} \\ =\frac{\sec ^2 A}{\operatorname{cosec}^2 A} \\ =\frac{1}{\frac{\cos ^2 A}{\frac{1}{\sin ^2 A}}} \\ =\frac{\sin ^2 A}{\cos ^2 A}=\tan ^2 A=\text { R.H.S. } \\ \text { M.H.S. }\left(\frac{1-\tan A}{1-\cot A}\right)^2 \\ =\frac{\left(1-\frac{\sin A}{\cos A}\right)^2}{\left(1-\frac{\cos A}{\sin A}\right)^2} \\ =\left(\frac{\cos A-\sin A}{\cos A} \times \frac{\sin A}{\sin A-\cos A}\right)^2 \\ =\left(\frac{\sin A}{\cos A}\right)^2=\tan ^2 A
L.H.S.=M.H.S.=R.H.S.
उपर्युक्त उदाहरणों द्वारा त्रिकोणमितीय सर्वसमिकाएं कक्षा 10 (Trigonometrical Identities Class 10),त्रिकोणमितीय सर्वसमिकाएं (Trigonometric Identities) को समझ सकते हैं।
3.त्रिकोणमितीय सर्वसमिकाएं कक्षा 10 के सवाल (Trigonometrical Identities Class 10 Questions):
सिद्ध कीजिएः
(1.) \sec ^6 \theta-\tan ^6 \theta=1+3 \tan ^2 \theta+3 \tan ^2 \theta
(2.) \tan ^2 A-\tan ^2 B=\frac{\cos ^2 B-\cos ^2 A}{\cos ^2 A \cos ^2 B}=\frac{\sin ^2 A-\sin ^2 B}{\cos ^2 A \cos ^2 B}
(3.) (\tan A+\operatorname{cosec} B)^2-(\cot B-\sec A)^2 =2 \tan A \cot B(\operatorname{cosec} A+\sec B)
उपर्युक्त सवालों को हल करने पर त्रिकोणमितीय सर्वसमिकाएं कक्षा 10 (Trigonometrical Identities Class 10),त्रिकोणमितीय सर्वसमिकाएं (Trigonometric Identities) को ठीक से समझ सकते हैं।
Also Read This Article:-Trigonometric Ratio of Specific Angles
4.त्रिकोणमितीय सर्वसमिकाएं कक्षा 10 (Frequently Asked Questions Related to Trigonometrical Identities Class 10),त्रिकोणमितीय सर्वसमिकाएं (Trigonometric Identities) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्नः
प्रश्नः1.त्रिकोणमितीय तीन मूलभूत सर्वसमिकाएं कौनसी हैं? (Which are Three Basic Trigonometric Identities?):
उत्तरःनिम्नलिखित तीन सर्वसमिकाएं मूलभूत सर्वसमिकाएं होती हैंः
\sin ^2 \theta+\cos ^2 \theta=1,1+\tan ^2 \theta=\sec ^2 \theta, 1+\cot ^2 \theta=cosec ^{2} \theta
प्रश्नः2.त्रिकोणमितीय सर्वसमिकाओं को सिद्ध करने के लिए किन बातों का ध्यान रखना चाहिए? (What Should be Taken into Account to Prove Trigonometric All-encompassing?):
उत्तरःत्रिकोणमितीय सर्वसमिकाओं को सिद्ध करते समय निम्नलिखित बिन्दुओं को ध्यान में रखना चाहिएः
(1.)सर्वसमिका के जटिल पक्ष में हल प्रारम्भ करते हैं और इसमें मूलभूत सर्वसमिकाओं का प्रयोग कर दूसरा पक्ष ज्ञात करते हैं।
(2.)यदि सर्वसमिकाओं में कई त्रिकोणमितीय अनुपात विद्यमान हो तो उनको sine अथवा cosine के रूप में व्यक्त करना सामान्यतया सुविधाजनक होता है।
(3.)यदि करणी चिन्ह (radical sign) लगा हो तो उसे यथासम्भव हटाना चाहिए।
(4.)यदि सर्वसमिका के एक पक्ष से दूसरा पक्ष सरलतापूर्वक ज्ञात नहीं किया जा सकता हो,तो दोनों पक्षों को सरल करके एक ही राशि अथवा पद के समानक सम (identically equal) सिद्ध करना चाहिए।
प्रश्नः3.क्या त्रिकोणमितीय अनुपातों में सभी सम्बन्ध त्रिकोणमितीय सर्वसमिकाएं हैं? (Are all Relations in Trigonometric Ratios Trigonometric Identities?):
उत्तरःत्रिकोणमितीय अनुपातों में सभी सम्बन्ध त्रिकोणमितीय सर्वसमिकाएं नहीं होती हैं जैसे \sin \theta=\cos \theta केवल एक त्रिकोणमितीय समीकरण है क्योंकि यह \theta के प्रत्येक मान के लिए सत्य नहीं है।
उपर्युक्त प्रश्नों के उत्तर द्वारा त्रिकोणमितीय सर्वसमिकाएं कक्षा 10 (Trigonometrical Identities Class 10),त्रिकोणमितीय सर्वसमिकाएं (Trigonometric Identities) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Trigonometrical Identities Class 10
त्रिकोणमितीय सर्वसमिकाएं कक्षा 10
(Trigonometrical Identities Class 10)
Trigonometrical Identities Class 10
त्रिकोणमितीय सर्वसमिकाएं कक्षा 10 (Trigonometrical Identities Class 10) को समझने से
पूर्व सर्वसमिका को समझना होगा।एक समीकरण को एक सर्वसमिका तब कहा जाता है जबकि
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.