Trigonometric Ratios of Special Angles
1.विशेष कोणों के त्रिकोणमितीय अनुपात (Trigonometric Ratios of Special Angles,Trigonometric Ratios of Some Specific Angle)-
विशेष कोणों के त्रिकोणमितीय अनुपात (Trigonometric Ratios of Special Angles,Trigonometric Ratios of Some Specific Angles) की कुछ प्रारम्भिक संकल्पनाओं जिसमें कोणों की माप,धनात्मक, ऋणात्मक कोण,त्रिकोणमितीय अनुपात,चतुर्थांशों में त्रिकोणमितीय अनुपातों के चिन्ह और सीमाओं का अध्ययन करेंगे।
(1.)चतुर्थांशों में त्रिकोणमितीय अनुपातों के चिन्ह (Signs of Trigonometric Ratios in Quardrants)-
माना परस्पर लम्बवत् दो सरल रेखाओं XOX’ और YOY’ का प्रतिच्छेद बिन्दु O है जिससे समतल चार चतुर्थांशों में विभक्त हो जाता है।इन चतुर्थांशों में त्रिकोणमितीय अनुपातों के चिन्ह नीचे दिए गए चित्रानुसार प्रदर्शित एवं याद किए जा सकते हैं।
इन्हें याद रखने की सरलतम विधि All,sin,tan,cos याद रखना है अर्थात् प्रथम चतुर्थांश में सभी त्रिकोणमितीय अनुपात धनात्मक है।द्वितीय चतुर्थांश में sin(cosec) धनात्मक है।इसी प्रकार तृतीय और चतुर्थ चतुर्थांशों में क्रमशः tan(cot) और cos(sec) धनात्मक है।
(2.)चतुर्थांशों में त्रिकोणमितीय अनुपातों के मानों की सीमाएं (Limits of Values of Trigonometric Ratios in Quardrants)-
[table id=3 /]
टिप्पणी:-चूंकि किसी संख्या (राशि) में भाग देना परिभाषित नहीं है इसलिए जब किसी भिन्न में a परिमित राशि और b \rightarrow 0(अर्थात् b,0 की ओर अग्रसर) हो तो का मान अपरिमित(∞) प्राप्त होता है जिसे अनन्त (infinity) पढ़ा जाता है।
(3.)कोण 0° के त्रिकोणमितीय अनुपातों के मान (Values of Trigonometrical Ratios of Angles 0°)-
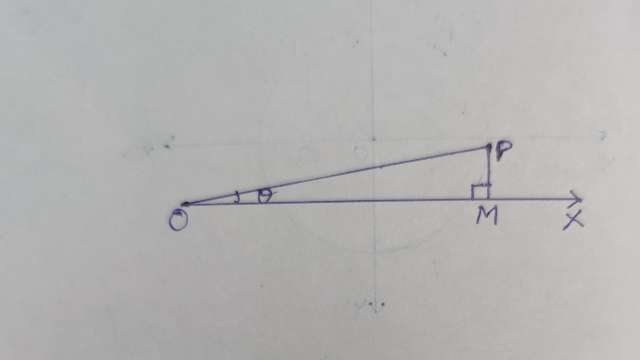
माना परिक्रामी रेखा OP, प्रारम्भिक स्थिति OX से परिभ्रभण करके वामावर्त (धनात्मक) दिशा में अतिलघु कोण \angle XOP=\theta बनाती है।बिन्दु P से OX पर लम्ब PM डालते हैं जिसका परिणाम बहुत छोटा है जैसे-जैसे रेखा OP, स्थिर रेखा OX की ओर अग्रसर होती है वैसे-वैसे MP की लम्बाई शून्य की ओर अग्रसर होती है और इस स्थिति में OP और OM सम्पाती हो जाती है और
\angle XOP=\theta \cong 0 और OP=OM
PM=0 (शून्य)
अतः O के संगत त्रिकोणमितीय अनुपातों के मान समकोण त्रिभुज OMP में निम्नलिखित होंगे।
\sin 0^{\circ}=\frac{P M}{O P}=\frac{\theta}{O P}=0 \\ \cos0^{\circ} =\frac{O M}{O P}=\frac{O P}{O p}=1 \\ \tan 0^{\circ}=\frac{P M}{O M}=\frac{0}{ OM }=0 \\ \cot 0^{\circ}=\frac{O M}{P M}=\frac{O M}{0}-\infty(अनन्त) \\ \sec 0^{\circ}=\frac{O P}{OM}=\frac{O P}{O P}=1
और \csc0^{\circ}=\frac{O P}{P M}=\frac{OP}{0}=\infty(अनन्त)
(4.) कोण 30° के त्रिकोणमितीय अनुपातों के मान (Values of Trigonometric Ratios of Angle 30°)-
माना परिक्रामी रेखा OP, प्रारम्भिक स्थिति OX से परिभ्रमण प्रारम्भ करके (धनात्मक) दिशा में \angle XOP=30^{\circ} कोण बनाती है।बिन्दु P से OX पर लम्ब PM डालते हैं।
समकोण त्रिभुज OMP में \therefore \angle OMP=90^{\circ} और \angle MOP=30^{\circ} \\ \therefore \angle OPM=60^{\circ}
अब PM को P’ तक आगे बढ़ाया जहां PM=MP’ और O, P’ को मिलाया।इस प्रकार दोनों त्रिभुजों OMP और OMP’ में भुजा OM और MP क्रमशः भुजा OM और MP’ के बराबर होगी एवं संगत कोण भी बराबर होंगे।
OP’=OP और \angle OP'P=\angle OPP'=60^{\circ}
अतः त्रिभुज P’OP समबाहु त्रिभुज होगा।
यदि OP=2a (माना) हो तो
MP=\frac{1}{2} p^{\prime} p=\frac{1}{2} OP=a
पुनः समकोण त्रिभुज OMP में बौधायन सूत्र से
OP^{2}=OM^{2}+MP^{2} \\ \therefore OM=\sqrt{OP^{2}-MP^{2}}=\sqrt{4{a}^{2}-a^{2}} \\=\sqrt{3}a
अतः त्रिकोणमितीय अनुपातों के मान
\sin 30^{\circ}=\frac{MP}{OP}=\frac{a}{2a}=\frac{1}{2} \\ \cos 30^{\circ}=\frac{OM}{OP}=\frac{a \sqrt{3}}{2 a}=\frac{\sqrt{3}}{2} \\ \tan 30^{\circ}=\frac{M P}{O M}=\frac{a}{a \sqrt{3}}=\frac{1}{\sqrt{3}} \\ \cot 30^{\circ}=\frac{OM}{PM}=\frac{a \sqrt{3}}{a}=\sqrt{3} \\ \sec 30^{\circ}=\frac{OM}{P M}=\frac{2 a}{a \sqrt{3}}=\frac{2}{\sqrt{3}}
और cosec30^{\circ}=\frac{OP}{PM}=\frac{2a}{a}=2
(5.)कोण 45° के त्रिकोणमितीय अनुपातों के मान (Values of Trigonometric Ratios of Angle 45°)-
माना एक परिक्रामी रेखा अपनी प्रारम्भिक स्थिति OX से वामावर्त दिशा में परिभ्रमण करते हुए स्थिति OP पर पहुंचती हैं और \angle XOP=45^{\circ} बनाती है।बिन्दु P से OX पर लम्ब PM डालते हैं।
समकोण त्रिभुज OMP में
\angle OMP=90 और \angle MOP=45 \\ \angle O P M=45^{\circ}
अतः त्रिभुज OPM समद्विबाहु भी होगा।
OM=PM
यदि OP=2a (माना) हो तो त्रिभुज OMP में बौधायन सूत्र से-
OP^{2}=OM^{2}+PM^{2} \\ 4a^{2}=OM^{2}+PM^{2}(\therefore OM=PM) \\ 4a^{2}=2OM^{2} \\\therefore OM=a \sqrt{2}
अतः त्रिकोणमितीय अनुपातों के मान
sin 45^{\circ}=\frac{PM}{OP}=\frac{a \sqrt{2}}{2 a}=\frac{1}{\sqrt{2}} \\ \cos 45^{\circ}=\frac{ON}{O P}=\frac{a \sqrt{2}}{2 a}=\frac{1}{\sqrt{2}} \\ \tan 45^{\circ}=\frac{PM}{O M}=\frac{a \sqrt{2}}{a \sqrt{2}}=1 \\ \cot 45^{\circ}=\frac{O M}{PM}=\frac{a \sqrt{2}}{a \sqrt{2}}=1 \\ \sec 45^{\circ}=\frac{O P}{O M}=\frac{2 a}{a \sqrt{2}}=\sqrt{2}
और {cosec} 45^{\circ}=\frac{O P}{OM}=\frac{2 a}{a \sqrt{2}}=\sqrt{2}
(6.)कोण 60° के त्रिकोणमितीय अनुपातों के मान (Values of Trigonometric Ratios of Angle 60°)-
माना एक परिक्रामी रेखा अपनी प्रारम्भिक स्थिति OX से वामावर्त दिशा में परिभ्रमण करते हुए स्थिति OP पर पहुंचकर \angle XOP=60^{\circ} बनाती है।बिन्दु P से OX पर लम्ब PM डालते हैं।
समकोण त्रिभुज OMP में \angle OMP=90^{\circ} और \angle MOP=60^{\circ} \\ \therefore \angle OPM=30^{\circ}
अब OX पर बिन्दु N इस प्रकार लेते हैं कि
MN=OM=a (माना)
इस प्रकार दोनों त्रिभुजों OMP और NMP में भुजा OM और PM क्रमशः भुजा NMऔर MP के बराबर होगी एवं संगत कोण भी बराबर होंगे।
PN=OP और \angle PNM=\angle POM=60^{\circ}
अतः त्रिभुज OPN समबाहु त्रिभुज होगा।
OP=ON=2OM=2a
पुनः समकोण त्रिभुज OMP में बौधायन सूत्र से-
OP^{2}=OM^{2}+MP^{2} \\ \therefore MP=\sqrt{OP^{2}-MP^{2}} \\ MP=\sqrt{4 a^{2}-a^{2}} \\ MP=\sqrt{3} a
अतः त्रिकोणमितीय अनुपातों के मान
sin 60^{\circ}=\frac{M P}{O P}=\frac{a \sqrt{3}}{2 a}=\frac{\sqrt{3}}{2} \\ \cos 60^{\circ}=\frac{ OM}{O P}=\frac{a}{2 a}=\frac{1}{2} \\ \tan 60^{\circ}=\frac{M P}{O M}=\frac{a \sqrt{3}}{a}=\sqrt{3} \\ \cot 60^{\circ}=\frac{1}{\tan 60^{\circ}}=\frac{1}{\sqrt{3}} \\ \sec 60=\frac{1}{\cos 60^{\circ}}=2
और cosec60^{\circ}=\frac{1}{\sin 60^{\circ}}=\frac{2}{\sqrt{3}}
(7.)कोण 90° के त्रिकोणमितीय अनुपातों के मान (Values of Trigonometric Ratios of Angle 90°)-
एक परिक्रामी रेखा OP, प्रारम्भिक स्थिति OX से परिभ्रमण प्रारम्भ करके वामावर्त दिशा में \angle XOP=\theta^{\circ} बनाती है जो कि कोण 90° (समकोण) के अत्यन्त समीप है परन्तु समकोण नहीं है। जैसे-जैसे रेखा OP समकोण की ओर अग्रसर होती है वैसे-वैसे OM की लम्बाई शून्य की ओर अग्रसर होगी और इस स्थिति में बिन्दु M,O के सम्पाती हो जाता है।
\angle XOP=\theta^{\circ} \cong 90° और OP=PM.OM=0 (शून्य)
अतः त्रिकोणमितीय अनुपातों के मान
\sin 90^{\circ}=\frac{MP}{OP}=\frac{OP}{OP}=1 \\ \cos 90^{\circ}=\frac{OM}{OP}=\frac{0}{OP}=0 \\ \tan 90^{\circ}=\frac{M P}{O M}=\frac{M P}{O}=\infty(अनन्त) \\ \cot 90^{\circ}=\frac{O M}{P M}=\frac{O}{M P}=0 \\ \sec 90^{\circ}=\frac{OP}{O M}=\frac{O P}{0}=\infty(अनन्त)
और cosec 90^{\circ}=\frac{O P}{P M}=\frac{OP}{OP}=1
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Complementary Angles in Trigonometry
2.विशेष कोणों के त्रिकोणमितीय अनुपातों की सारणी (Trigonometric Ratios of Special Angles Table,Trigonometric Ratios of Some Specific Angles Table),मानक कोणों के त्रिकोणमितीय अनुपात (Trigonometric Ratios of Standard Angles),मानक कोणों के त्रिकोणमितीय अनुपातों की सारणी (Trigonometric Ratios of Standard Angles Table)-
त्रिकोणमिति तालिका: त्रिकोणमिति तालिका में मानक कोणों के लिए विभिन्न त्रिकोणमितीय अनुपातों के मान शामिल हैं – 0°,30°,45°,60° और 90°। साइन (sine), कोसाइन(cosine), टैंजेंट(tangent), कॉटैंजेंट(cotangent), सेकेंट(secant) और कोसेकेंट(cosecant) छह त्रिकोणमितीय अनुपात हैं। त्रिकोणमिति तालिका विभिन्न कोणों के लिए इन त्रिकोणमितीय अनुपातों के मूल्यों को दर्शाती है।इन मूल्यों को जानने से विभिन्न त्रिकोणमितीय समस्याओं को हल करना आसान हो सकता है।
त्रिकोणमिति गणित की वह शाखा है जो एक त्रिभुज की भुजाओं और कोणों के बीच के संबंध से संबंधित है। आमतौर पर, यह समकोण त्रिभुजों से जुड़ा होता है, जिसमें त्रिभुज के तीन कोणों में से एक समकोण होता है।यह गणना को सरल बनाने और ज्यामितीय समस्याओं की एक विस्तृत विविधता को हल करने में मदद करता है।
उदाहरण के लिए, यदि आप ज्ञात ऊँचाई की एक ऊँची इमारत की छत पर हैं और सड़क के दूसरी तरफ एक पोस्ट बॉक्स है, तो इमारत के ऊपर आपकी स्थिति, इमारत के शीर्ष पर (प्वाइंट A),भवन के पाद (प्वाइंट B),और पोस्ट बॉक्स का स्थान (प्वाइंट C) एक समकोण त्रिभुज बनाता है।आप आसानी से त्रिकोणमिति का उपयोग करके सड़क की चौड़ाई की गणना कर सकते हैं।निर्माण, उड़ान इंजीनियरिंग,अपराध विज्ञान, समुद्री जीव विज्ञान और इंजीनियरिंग आदि के क्षेत्र में त्रिकोणमिति के विभिन्न अनुप्रयोग हैं।
यह आलेख आपको त्रिकोणमिति अनुपात तालिका और तालिका याद करने के लिए ट्रिक्स प्रदान करेगा ताकि आप समस्याओं को हल करने के लिए सीधे उनका उपयोग कर सकें।
त्रिकोणमितीय अनुपातों के विशेष कोणों 0°,30°,45°,60° और 90° के मान उपर्युक्त अनुच्छेदों में ज्ञात किए हैं जिन्हें सारणीबद्ध निम्न प्रकार लिखा जा सकता है।
[table id=2 /]
3.विशेष कोणों के त्रिकोणमितीय अनुपातों के उदाहरण (Trigonometric Ratios of Special Angles Examples,Trigonometric Ratios of Some Specific Angles Examples)-
निम्न के मान ज्ञात कीजिए:
Example-1.2 \sin 45^{\circ} \cos 45^{\circ}
Solution- 2\sin 45^{\circ} \cos 45^{\circ} \\ =2 \times \frac{1}{\sqrt{2}} \times \frac{1}{\sqrt{2}} \\ =1
Example-2.\cos 45^{\circ} \cos 60^{\circ}-\sin 45^{\circ} \sin 60^{\circ}
Solution-\cos 45^{\circ} \cos 60^{\circ}-\sin 45^{\circ} \sin 60^{\circ} \\ =\left(\frac{1}{\sqrt{2}}\right)\left(\frac{1}{2}\right)-\left(\frac{1}{\sqrt{2}}\right)\left(\frac{\sqrt{3}}{2}\right) \\ =\frac{1}{2 \sqrt{2}}-\frac{\sqrt{3}}{2 \sqrt{2}} \\ =\frac{1-\sqrt{3}}{2 \sqrt{2}}
Example-3.\sin ^{2} 30^{\circ}+2 \cos ^{2} 45^{\circ}+3 \tan ^{2} 60^{\circ}
Solution-\sin ^{2} 30^{\circ}+2 \cos ^{2} 45^{\circ}+3 \tan ^{2} 60^{\circ} \\ \text { sin }^{2} 30^{\circ}+2 \cos ^{2} 45^{\circ}+3 \tan ^{2} 60^{\circ} \\ \frac{1}{4}\left(\frac{1}{2}\right)+2\left(\frac{1}{\sqrt{2}}\right)^{2}+3(\sqrt{3})^{2} \\ \frac{1}{4}+\frac{2}{2}+\frac{9}{8} \\ =\frac{1}{4}+1+9 \\ =\frac{1+4+36}{4} \\ =\frac{41}{4} \\ =10 \frac{1}{4}
Example-4.3 \sin ^{2} 60^{\circ}-4 \sin ^{3} 60^{\circ}
Solution- 3 \sin ^{2} 60^{\circ}-4 \sin ^{3} 60^{\circ} \\ =3\left(\frac{\sqrt{3}}{2}\right)^{2}-4\left(\frac{\sqrt{3}}{2}\right)^{3} \\ =3 \times \frac{3}{4}-4 \times \frac{3 \sqrt{3}}{8} \\ =\frac{9}{4}-\frac{3 \sqrt{3}}{2} \\ =\frac{9-6 \sqrt{3}}{4}
Example-5.\frac{5 \cos ^{2} 60^{\circ}+4 \sec ^{2} 30^{\circ}-\tan ^{2} 45^{\circ}}{\sin ^{2} 30^{\circ}+\cos ^{2} 30^{\circ}}
Solution-\frac{5 \cos ^{2} 60^{\circ}+4 \sec ^{2} 30^{\circ}-\tan ^{2} 45^{\circ}}{\sin ^{2} 30^{\circ}+\cos ^{2} 30^{\circ}} \\ = \frac{5\left(\frac{1}{2}\right)^{2}+4\left(\frac{2}{\sqrt{3}}\right)^{2}-(1)^{2}}{\left(\frac{1}{2}\right)^{2}+\left(\frac{\sqrt{3}}{2}\right)^{2}} \\ =\frac{\frac{5}{4}+\frac{16}{3}-\frac{1}{1}}{\frac{1}{4}+\frac{3}{4}} \\ = \frac{\frac{15+64-12}{12}}{\frac{1+3}{4}} \\ =\frac{67}{12}
Example-6.\cot ^{2} 45^{\circ}-\sec ^{2} 60^{\circ}+\sin ^{2} 60^{\circ}+ \cos ^{2} 90^{\circ}
Solution-\cot ^{2} 45^{\circ}-\sec ^{2} 60^{\circ}+\sin ^{2} 60^{\circ}+ \cos ^{2} 90^{\circ}\\ =4 \cot ^{2} 45^{\circ}-\sec ^{2} 60^{\circ}+\sin ^{2} 60^{\circ}+\cos ^{2} 90^{\circ} \\ ={4(1)^{2}-(2)^{2}+\left(\frac{\sqrt{3}}{2}\right)^{2}+(0)^{2}} \\ =4-4+\frac{3}{4}+0 \\ =\frac{3}{4}
Example-7.\frac{4}{\cot ^{2} 30}+\frac{1}{\sin ^{2} 30^{\circ}}-\cos ^{2} 45^{\circ}
Solution-\frac{4}{\cot ^{2} 30}+\frac{1}{\sin ^{2} 30^{\circ}}-\cos ^{2} 45^{\circ} \\ =\frac{4}{(\sqrt{3})^{2}}+\frac{1}{\left(\frac{1}{2}\right)^{2}}-\left(\frac{1}{\sqrt{2}}\right)^{2} \\ =\frac{4}{3}+\frac{4}{1}-\frac{1}{2} \\ =\frac{8+24-3}{6} \\ =\frac{29}{6}
Example-8.\frac{\tan ^{2} 60^{\circ}+4 \sin ^{2} 45^{\circ}+\sin ^{2} 90^{\circ}}{3 \sec ^{2} 60^{\circ}+cosec^{2} 60^{\circ}-\cot ^{2} 30^{\circ}}
Solution-\frac{\tan ^{2} 60^{\circ}+4 \sin ^{2} 45^{\circ}+\sin ^{2} 90^{\circ}}{3 \sec ^{2} 60^{\circ}+cosec^{2} 60^{\circ}-\cot ^{2} 30^{\circ}} \\ =\frac{(\sqrt{3})^{2}+4\left(\frac{1}{\sqrt{2}}\right)^{2}+(1)^{2}}{3(2)^{2}+\left(\frac{2}{\sqrt{3}}\right)^{2}-(\sqrt{3})^{2}} \\ =\frac{3+2+1}{12+\frac{4}{3}-3} \\ =\frac{6}{\frac{36+4-9}{3}} \\ =\frac{18}{31}
निम्न में x का मान ज्ञात कीजिए:
Example-9. \cos x=\cos 60^{\circ} \cos 30^{\circ}+\sin 60^{\circ} \sin 30^{\circ}
Solution- \cos x=\cos 60^{\circ} \cos 30^{\circ}+\sin 60^{\circ} \sin 30^{\circ} \\ \Rightarrow \cos x=\left(\frac{1}{2}\right)\left(\frac{\sqrt{3}}{2}\right)+\left(\frac{\sqrt{3}}{2}\right)\left(\frac{1}{2}\right) \\ \Rightarrow \cos x=\frac{\sqrt{3}}{4}+\frac{\sqrt{3}}{4} \\ \Rightarrow \cos x=\frac{2\sqrt{3}}{4} \\ \Rightarrow \cos x=\frac{\sqrt{3}}{2} \\ \Rightarrow \cos x=\cos 30^{\circ} \\ \Rightarrow x= 30^{\circ}
Example-10.\sin 2 x=\sin 60^{\circ} \cos 30^{\circ}-\cos 60^{\circ} \sin 30^{\circ}
Solution-\sin 2 x=\sin 60^{\circ} \cos 30^{\circ}-\cos 60^{\circ} \sin 30^{\circ} \\ \Rightarrow \sin 2 x=\left(\frac{\sqrt{3}}{2}\right)\left(\frac{\sqrt{3}}{2}\right)-\left(\frac{1}{2}\right)\left(\frac{1}{2}\right) \\ \Rightarrow \sin 2 x=\frac{3}{4}-\frac{1}{4} \\ \Rightarrow \sin 2 x=\frac{2}{4} \\ \Rightarrow \sin 2 x=\frac{1}{2} \\ \Rightarrow \sin 2 x=\sin 30^{\circ} \\ \Rightarrow 2x =30^{\circ} \\ \Rightarrow x =15^{\circ}
Example-11.\sqrt{3} \tan 2 x=\sin 30^{\circ}+\sin 45^{\circ} \cos 45^{\circ}+2 \sin 90^{\circ}
Solution-\sqrt{3} \tan 2 x=\sin 30^{\circ}+\sin 45^{\circ} \cos 45^{\circ}+2 \sin 90^{\circ} \\ \Rightarrow \sqrt{3} \tan 2 x=\frac{1}{2}+\left(\frac{1}{\sqrt{2}}\right)\left(\frac{1}{2}\right)+2(1) \\ \Rightarrow \sqrt{3} \tan 2 x=\frac{1}{2}+\frac{1}{2}+2 \\ \Rightarrow \sqrt{3} \tan 2 x=\frac{1+1+4}{2} \\ \Rightarrow \sqrt{3} \tan 2 x=\frac{6}{2} \\ \Rightarrow \sqrt{3} \tan 2 x=3 \\ \Rightarrow \tan 2 x=\frac{3}{\sqrt{3}} \\ \Rightarrow \tan 2 x=\sqrt{3} \\ \Rightarrow \tan 2 x=\tan 60^{\circ} \\ \Rightarrow 2x=60^{\circ} \\ \Rightarrow x=\frac{60^{\circ}}{2} \\ \Rightarrow x=30^{\circ}
Example-12.सिद्ध कीजिए: 4 \sin 30^{\circ} \sin ^{2} 60^{\circ}+3 \cos 60^{\circ}+\tan 45^{\circ}=2 \sec ^{2} 45^{\circ}-cosec^{2} 90^{\circ}
Solution-4 \sin 30^{\circ} \sin ^{2} 60^{\circ}+3 \cos 60^{\circ}+\tan 45^{\circ}=2 \sec ^{2} 45^{\circ}-cosec^{2} 90^{\circ} \\ L.H.S = \quad 4 \sin 30^{\circ} \sin ^{2} 60^{\circ}+3 \cos 60^{\circ} \tan 45^{\circ} \\ =4\left(\frac{1}{2}\right)\left(\frac{\sqrt{3}}{2}\right)^{2}+3\left(\frac{1}{2}\right)(1) \\ =\frac{3}{2}+\frac{3}{2} \\ =\frac{6}{2}=3 \\ R.H.S=2 \sec ^{2} 45^{\circ}-cosec^{2} 90^{\circ} \\ =2(\sqrt{2})^{2}-(1)^{2} \\ =4-1=3
Example-13. सिद्ध कीजिए:2\left(\cos ^{2} 45^{\circ}+\tan ^{2} 60^{\circ}\right)-6\left(\sin ^{2} 45^{\circ}-\tan ^{2} 30^{\circ}\right)=6
Solution-2\left(\cos ^{2} 45^{\circ}+\tan ^{2}60^{\circ}\right)-6\left(\sin ^{2} 45^{\circ}-\tan ^{2} 30^{\circ}\right)=6 \\ L.H.S=2\left(\cos ^{2} 45^{\circ}+\tan ^{2} 6^{\circ}\right)-6\left(\sin ^{2} 45^{\circ}-\tan ^{2} 30^{\circ}\right) \\ =2[(\frac{1}{\sqrt{2}})^{2}+(\sqrt{3})^{2} ]-6[(\frac{1}{\sqrt{2}})^{2}-(\frac{1}{\sqrt{3}})^{2}] \\ =2\left(\frac{1}{2}+3\right)- 6\left(\frac{1}{2}-\frac{1}{3}\right) \\ =2\left(\frac{1+6}{2}\right)-6\left(\frac{3-2}{6}\right) \\ =7-1=6=R.H.S
Example-14.यदि x=30° हो तो सिद्ध कीजिए:sin 3 x=3 \sin x-4 \sin 3 x
Solution-\sin 3 x =3 \sin x-4 \sin 3 x \\L.H.S= \sin 3 x =\sin 3\left(30^{\circ}\right) . \\ =\sin 90^{\circ} \\ =1 \\ R.H.S=3 \sin x-4 \sin ^{3} x \\ =3 \sin 30^{\circ}-4 \sin ^{3} 30^{\circ} \\ =3\left(\frac{1}{2}\right)-4\left(\frac{1}{2}\right)^{3} \\ =\frac{3}{2}-4 \times \frac{1}{8} \\ =\frac{3}{2}-\frac{1}{2}=\frac{2}{2}=1
Example-15.यदि x=30° हो तो सिद्ध कीजिए:\tan2x=\frac{2 \tan x}{1-\tan^{2} x}
Solution-\tan2x=\frac{2 \tan x}{1-\tan^{2} x} \\ L.H.S=\tan2x \\ =\tan2(30^{\circ}) \\ =\tan(60^{\circ}) \\ =\sqrt3 \\ R.H.S=\frac{2 \tan x}{1-\tan^{2} x} \\ \frac{2 \tan 30^{\circ}}{1-\tan ^{2} 30^{\circ}} \\ =2 \frac{1}{1-\left(\frac{1}{\sqrt{3}}\right)^{2}} \\ =\frac{\frac{2}{\sqrt{3}}}{1-\frac{1}{3}} \\ =\frac{2^{3}}{\frac{2}{2}} \\ =\frac{2}{\sqrt{3}} \times \frac{3}{2} \\ =\sqrt{3}
Example-16.यदि x=30° हो तो सिद्ध कीजिए: \sin x =\sqrt{\frac{1-\cos 2 x}{2}} \\ -1+5=\sin x \\ =\sin 30=\frac{1}{2}
Solution:-\sin x =\sqrt{\frac{1-\cos 2 x}{2}} \\ L.H.S=\sin x \\ =\sin 30=\frac{1}{2} \\ R.H.S=\sqrt{\frac{1-\cos 2 x}{2}}=\sqrt{\frac{1-\cos 2\left(30^{\circ}\right)}{2}} \\ =\sqrt{\frac{1-\cos 60^{\circ}}{2}} \\ =\sqrt{\frac{1-\frac{1}{2}}{2}} \\ =\sqrt{\frac{\frac{1}{2}}{2}} \\ =\sqrt\frac{1}{2}=\frac{1}{2}
Example-17.यदि A=60° और B=30° हो तो सिद्ध कीजिए:\cot (A-B)=\frac{\cot A \cot B +1}{\cot B-\cot A}
Solution-\cot (A-B)=\frac{\cot A \cot B +1}{\cot B-\cot A} \\ L.H.S=\cot (A-B) \\ =\cot (60^{\circ}-30^{\circ}) \\ =\cot 30^{\circ}=\sqrt{3} \\ R.H.S=\frac{\cot A \cot B +1}{\cot B-\cot A} \\ = \frac{\cos 60^{\circ} \cot 30^{\circ}+1}{\cot 30^{\circ}-\cot 60^{\circ}} \\ = \frac{\left(\frac{1}{\sqrt{3}}\right)(\sqrt{3})+1}{\sqrt{3}-\left(\frac{1}{\sqrt{3}}\right)} \\ = \frac{1+1}{\frac{3-1}{\sqrt{3}}} \\ = 2 \times \frac{\sqrt{3}}{2}=\sqrt{3}
उपर्युक्त उदाहरणों के द्वारा विशेष कोणों के त्रिकोणमितीय अनुपात (Trigonometric Ratios of Special Angles,Trigonometric Ratios of Some Specific Angles) को समझ सकते हैं।
4.विशेष कोणों के त्रिकोणमितीय अनुपातों की समस्याएं (Trigonometric Ratios of Special Angles Problems,Trigonometric Ratios of Some Specific Angles Problems)-
निम्न के मान ज्ञात कीजिए:
(1.) \frac{2 \tan 30^{\circ}}{1-\tan ^{2} 30^{\circ}} \\ (2.) \frac{\sin 30^{\circ}-\sin 90^{\circ}+2 \cos 0^{\circ}}{\tan 30^{\circ} \cdot \tan 60^{\circ}}
(3.) सिद्ध कीजिए:\frac{\sin 60^{\circ}+\sin 30^{\circ}}{\sin 60^{\circ}-\sin 30^{\circ}}=\frac{\tan 60^{\circ}+\tan 45^{\circ}}{\tan 60^{\circ}-\tan 45^{\circ}}
(4.) सिद्ध कीजिए:\frac{\cos 30+ \sin 30^{\circ}}{1+\sin 60 \sin 30^{\circ}}=\frac{\sqrt{3}}{2}
(5.) सिद्ध कीजिए: cosec^{2} 45^{\circ} \sec ^{2} 30^{\circ} \sin ^{3} 90 \cos 60^{\circ}=\frac{4}{3}
(6.) सिद्ध कीजिए: \frac{\sin 60^{\circ}+\sin 30^{\circ}}{\sin 60^{\circ}-\sin 30^{\circ}}=\frac{\tan 60^{\circ}+\tan 45^{\circ}}{\tan 60^{\circ}-\tan 45^{\circ}}
(7.) सिद्ध कीजिए:\left(\sec ^{2} 30^{\circ}+cosec^{2} 45^{\circ}\right)\left(2 \cos 60^{\circ}+\sin 90^{\circ}+\tan 45^{\circ}\right)=10
(8.) सिद्ध कीजिए:\left(1-\sin 45^{\circ}+\sin 30^{\circ}\right)\left(1+\cos 45^{\circ}+\cos 60^{\circ}\right)=\frac{7}{4}
(9.) सिद्ध कीजिए: \left( \cos ^{2} 0^{\circ}-2 \cot ^{2} 30^{\circ}+3 cosec^{2} 90^{\circ}=2\left(\sec ^{2} 45^{\circ}-\tan ^{2} 60^{\circ}\right)\right.
(10.)यदि x=30° हो तो सिद्ध कीजिए: \cos 3 x=4 \cos ^{3} x-3 \cos x
उत्तर (Answer): (1) \sqrt3 \\ (2) \frac{3}{2}
उपर्युक्त सवालों को हल करने पर विशेष कोणों के त्रिकोणमितीय अनुपात (Trigonometric Ratios of Special Angles,Trigonometric Ratios of Some Specific Angles) ठीक से समझ सकते हैं।
5.विशेष कोणों के त्रिकोणमितीय अनुपातों की परिभाषा Trigonometric Ratios of Special Angles Definition),विशेष कोणों के त्रिकोणमितीय अनुपात क्या हैं? (What is trigonometric ratios of special angles)-
त्रिकोणमिति में,0°,30°,45°,60° और 90° को विशेष कोण कहा जाता है और वे हमेशा प्रथम चतुर्थांश में स्थित होते हैं।ये विशेष कोण 0°, 30°, 45° और 60°अक्सर अनुप्रयोगों में देखे जाते हैं और हम इन कोणों के त्रिकोणमितीय अनुपात को निर्धारित करने के लिए ज्यामिति का उपयोग कर सकते हैं।
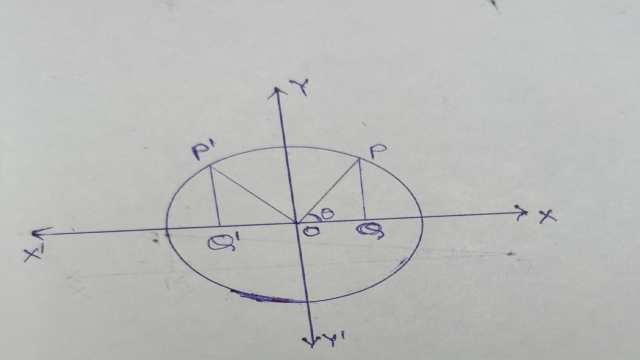
मॉड्यूल में आगे त्रिकोणमिति,हमने दिखाया कि यूनिट सर्कल पर बिंदुओं के निर्देशांक के संदर्भ में त्रिकोणमितीय फलनों को कैसे फिर से परिभाषित किया जाए।यह त्रिकोणमितीय फलनों की परिभाषा को दूसरे चतुर्थांश तक विस्तारित करने की अनुमति देता है।
यदि कोण पहले चतुर्थांश से संबंधित है,तो आरेख में दिखाए गए इकाई सर्कल पर बिंदु P के निर्देशांक बस (cosθ, sinθ) हैं।
इस प्रकार, यदि θ,OP और धनात्मक x-अक्ष के बीच का कोण है:
कोसाइन (cosine) को इकाई वृत्त पर बिंदु P के x-निर्देशांक के रूप में परिभाषित किया गया है
sine को इकाई वृत्त पर बिंदु P के y-निर्देशांक के रूप में परिभाषित किया गया है।
हम इस परिभाषा को किसी भी कोण पर लागू कर सकते हैं।
फिर स्पर्शज्या(tangent) अनुपात द्वारा परिभाषित किया गया है
tanθ = sinθ/cosθ,
बशर्ते cosθ शून्य न हो।
एक उदाहरण के रूप में हम θ को 30°लेते है, इसलिए P में निर्देशांक (cos30∘, sin30) हैं।अब बिंदु P को सर्कल के चारों ओर P’ पर ले जाएं, ताकि OP′, धनात्मक x-अक्ष के साथ 150° का कोण बनाता है।ध्यान दें कि 30°30 और 150° सम्पूरक कोण हैं।P’ के निर्देशांक हैं (cos150°, sin150°।)।
6.विशिष्ट कोणों के त्रिकोणमितीय अनुपात को सीखने का आसान तरीका (Easy way to Learn Trigonometric Ratios of Specific Angles)-
त्रिकोणमिति अनुपात तालिका याद करने से आप विभिन्न समस्याओं को आसानी से हल कर सकते हैं।इसलिए, यदि आप त्रिकोणमिति तालिका ट्रिक्स ढूंढ रहे हैं,तो आप सही जगह पर आए हैं।
यदि आप त्रिकोणमिति सूत्रों को पहले से जानते हैं, तो त्रिकोणमिति अनुपात तालिका को याद रखना आपके लिए बेहद आसान होगा।इसके अलावा,अपनी उंगलियों पर सूत्रों के साथ, आप भूल जाने पर भी किसी भी बिंदु पर मूल्यों की गणना कर सकते हैं।
आइए पहले नीचे सूचीबद्ध त्रिकोणमिति सूत्रों को पुनस्मरण करते हैं और याद करते हैं:
sin x = cos (90°-x)
cos x = sin (90°-x)
tan x = cot (90°-x)
cot x = tan (90°-x)
sec x = cosec (90°-x)
cosec x = sec (90°-x)
1/sin x = cosec x
1/cos x = sec x
1/tan x = cot x
7.विशेष कोणों के त्रिकोणमितीय अनुपात को कैसे याद किया जाए? (How to Memorize Trigonometric Ratios of Special Angles?)-
मेरे गणित के प्रोफेसर ने हाल ही में हमें बताया कि वह चाहते थे कि हम स्नैप पर हमारे सिर में sin(π/2) का जवाब देने में सक्षम हों।मुझे पता है कि मैं इस शुक्रवार तक परीक्षण के लिए तालिका को याद कर सकता हूं, लेकिन मैं शायद परीक्षण के बाद उन्हें भूल सकता हूं।तो क्या कोई ट्रिक या पैटर्न है जो आप लोग आमतौर पर इसे याद करने के लिए इस्तेमाल करते हैं?उदाहरण के लिए, SOHCAHTOA हमें बताता है कि साइन(sine),कोसाइन(cosine) और स्पर्शज्या(tangent) का वास्तव में क्या मतलब है।
यदि नहीं, तो मैं सिर्फ सारणी को याद करूंगा।लेकिन सिर्फ यह जानना चाहते थे कि आप लोग किन यादगार तकनीकों का इस्तेमाल करते हैं।मुझे लगता है कि यह पूछने के लिए एकदम सही जगह है, क्योंकि मैंने सत्यम मैथमेटिक्स में लोगों के एक समूह को ट्रिक दिया है।
पहले सरल उदाहरण पर विचार करें और फिर आप इससे आगे के मूल्यों को प्राप्त कर सकते हैं।निम्नलिखित तालिका से शुरू करते हैं।sin,cos,tan टेबल
आपको इस तालिका के बारे में याद रखने की आवश्यकता है कि पंक्तियों और स्तंभों की व्यवस्था यानी कोणों को पंक्तियों में और त्रिकोणमितीय फलनों में रखा गया है।तो एक तालिका बनाएं और साइन (sin) मूल्यों के साथ शुरू करें।
चरण 1 (लाल): 0°,30°,45°,60° और 90° लिखो (0,1,2,3,4) की साइन के लिए प्रत्येक खाली कोशिकाओं में।
चरण 2 (हरा): फिर उनमें से प्रत्येक को 4 (यानी 0/4, 1/4, 2/4, 3/4, 4/4) से विभाजित करें।
चरण 3 (नीला): अगला चरण प्रत्येक का वर्गमूल (यानी \sqrt (0/4), \sqrt (1/4),\sqrt (2/4), \sqrt) (3/4), \sqrt (4/4 ) लेना है।)।
चरण 4 (भूरा): अब यदि लागू हो और परिणामों को सरल बनाने के लिए अंश और हर से किसी भी पद को समाप्त करें।आप साइन 0°,30°,45°,60° और 90° के मूल्यों के साथ समाप्त होते हैं।
ड्राइंग sin,cos,tan टेबल
चरण 5 (नारंगी): एक बार जब आपके पास साइन (sin) फंक्शन के लिए मान होते हैं, तो उन्हें कॉसिन (cosine) के लिए उल्टा कर दें (sin90 = cos0, sin60 = cos30, sin45 = cos45 और इसी तरह) और आपको cosine फ़ंक्शन के मान मिलते हैं।
चरण 6: स्पर्शज्या (tangent) के लिए sin/cos मान डालें और सरल करें।
चरण 7: आप इस तरह के सूत्रों का उपयोग करके तालिका को आगे के कोणों के लिए बढ़ा सकते हैं
sin (π/2-x) = cosx और cos (π / 2) −x) = sinx
उपर्युक्त उदाहरणों, सवालों को हल करके तथा प्रश्नों के उत्तर द्वारा हम विशेष कोणों के त्रिकोणमितीय अनुपात (Trigonometric Ratios of Special Angles,Trigonometric Ratios of Some Specific Angle) को भली-भांति समझ सकते हैं।
Also Read This Article:-Trigonometric Identities Formula
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |