Trigonometric Ratios of Acute Angle
1.न्यून कोणों के त्रिकोणमितीय अनुपात (Trigonometric Ratios of Acute Angle)-
- न्यून कोणों के त्रिकोणमितीय अनुपात (Trigonometric Ratios of Acute Angle) समकोण त्रिभुज के लिए ज्ञात करना सीखेंगे।
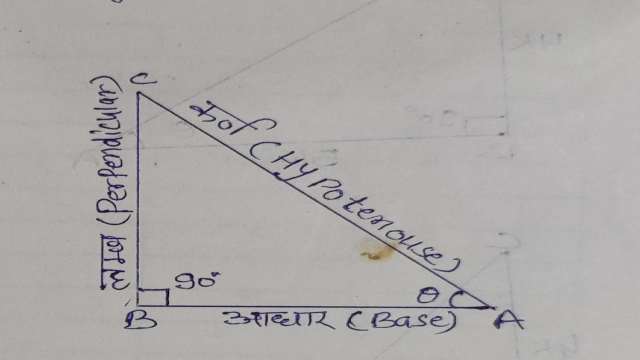
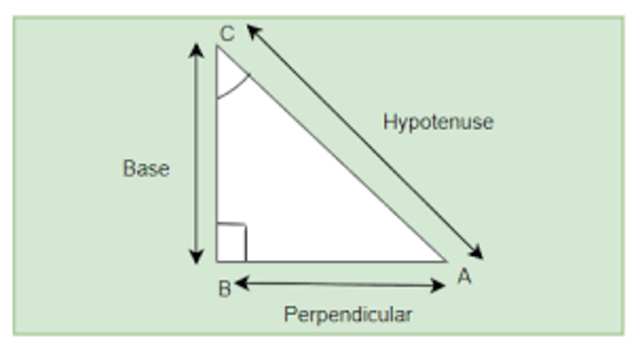
- समकोण त्रिभुज जिसका एक कोण समकोण है। समकोण के सम्मुख भुजा को कर्ण कहते हैं।किसी समकोण त्रिभुज के अन्य दो कोणों के सन्दर्भ में किसी कोण को बनाने वाली कर्ण के अतिरिक्त दूसरी भुजा आधार अथवा आसन्न भुजा तथा इस कोण की सम्मुख भुजा लम्ब कहलाती है।किसी समकोण त्रिभुज में किन्हीं दो भुजाओं के अनुपात को त्रिकोणमितीय अनुपात कहते हैं।
- माना ABC एक समकोण त्रिभुज है जिसमें \angle ABC समकोण तथा \angle CAB=\theta हो तो
(1)\sin { \theta } =\frac { लम्ब }{ कर्ण } =\frac { BC }{ AC } \\ (2)\cos { \theta } =\frac {आधार }{कर्ण } =\frac { AB }{ AC } \\ (3)\tan { \theta } =\frac { लम्ब }{ आधार} =\frac { BC }{ AB } \\ (4)cosec\theta = \frac { कर्ण }{लम्ब }=\frac { AC }{ BC } \\ (5)\sec { \theta } =\frac { कर्ण }{ आधार } =\frac { AC }{ AB } \\ (6)\cot { \theta } = \frac { आधार }{लम्ब }=\frac { AB }{ BC }
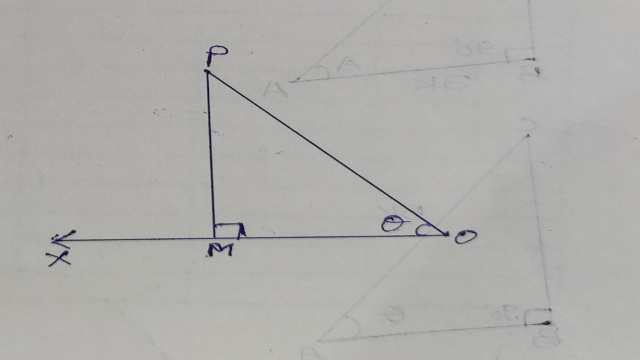
- मान लीजिए एक परिक्रामी रेखा OX ,अपनी आदि स्थिति OX से शीर्ष O के सापेक्ष वामावर्त दिशा में परिक्रामी करती हुई एक धनात्मक न्यूनकोण \angle XOP=\theta बनाती है।
- जैसा कि चित्र में दिखाया गया है।बिन्दु P से OX पर लम्ब PM खींचो।इस प्रकार हमें समकोण त्रिभुज OMP प्राप्त होता है। जिसमें समकोण के सामने की भुजा OP ,त्रिभुज का कर्ण है।
कोण =\theta के सन्दर्भ में OM को आसन्न भुजा (आधार) तथा PM को सम्मुख भुजा (लम्ब) कहेंगे। - समकोण त्रिभुज OMP की भुजाओं की लम्बाइयों का प्रयोग करते हुए हम न्यून कोण =\theta में उपर्युक्त छ: विभिन्न त्रिकोणमितीय अनुपातों (अथवा फलनों) को परिभाषित करते हैं:
- आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं। इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Rationalization of denominator
2.न्यून कोणों के त्रिकोणमितीय अनुपात के उदाहरण और हल (Trigonometric Ratios of Acute Angle Examples and Solutions),न्यून कोण के त्रिकोणमितीय फलनों की समस्याएं हल सहित (Trigonometric functions of acute angles problems with solutions)-
Example-1. यदि \triangle ABC में \angle A={ 90 }^{ 0 },a=25 सेमी,b=7 सेमी हो तो \angle B और \angle C के लिए सभी त्रिकोणमितीय अनुपात लिखिए।
Solution-समकोण \triangle ABC में
{ BC }^{ 2 }={ AB }^{ 2 }+{ AC }^{ 2 }\\ \Rightarrow { AB }^{ 2 }={ BC }^{ 2 }-{ AC }^{ 2 }\\ \Rightarrow { AB }^{ 2 }={ 25 }^{ 2 }-{ 7 }^{ 2 }\\ \Rightarrow { AB }^{ 2 }=625-49\\ \Rightarrow { AB }^{ 2 }=576\\ \Rightarrow { AB }=24\\ \sin { B } =\frac { AC }{ BC } =\frac { 7 }{ 25 } \\ \cos { B } =\frac { AB }{ BC } =\frac { 24 }{ 25 } \\ \tan { B } =\frac { AC }{ AB } =\frac { 7 }{ 24 } \\ \cot { B } =\frac { AB }{ AC } =\frac { 24 }{ 7 } \\ \sec { B } =\frac { BC }{ AB } =\frac { 25 }{ 24 } \\ cosecB=\frac { BC }{ AC } =\frac { 25 }{ 7 } \\ \sin { C } =\frac { AB }{ BC } =\frac { 24 }{ 25 } \\ \cos { C } =\frac { AC }{ BC } =\frac { 7 }{ 25 } \\ \tan { C } =\frac { AB }{ AC } =\frac { 24 }{ 7 } \\ \cot { C } =\frac { AC }{ AB } =\frac { 7 }{ 24 } \\ \sec { C } =\frac { BC }{ AC } =\frac { 25 }{ 7 } \\ cosecC=\frac { BC }{ AB } =\frac { 24 }{ 25 }
Example-2. यदि \tan { A } =\sqrt { 2 } -1 तो सिद्ध कीजिए कि \sin { A } \cos { A } =\frac { 1 }{ 2\sqrt { 2 } }
Solution-\tan { A } =\sqrt { 2 } -1\\ \Rightarrow \tan { A } =\frac { \sqrt { 2 } -1 }{ 1 }
लम्ब=\sqrt { 2 } -1 , आधार=1
कर्ण=\sqrt { { (लम्ब) }^{ 2 }+{ (आधार) }^{ 2 } } \\ =\sqrt { { \left( \sqrt { 2 } -1 \right) }^{ 2 }+{ \left( 1 \right) }^{ 2 } } \\ =\sqrt { 2+1-2\sqrt { 2 } +1 } \\ =\sqrt { 4-2\sqrt { 2 } } \\ =\sqrt { 2\sqrt { 2 } \left( \sqrt { 2 } -1 \right) }
\sin { A } =\frac { लम्ब }{ कर्ण } \\ \sin { A } =\frac { \sqrt { 2 } -1 }{ \sqrt { 2\sqrt { 2 } \left( \sqrt { 2 } -1 \right) } } \\ \Rightarrow \sin { A } =\frac { \sqrt { \left( \sqrt { 2 } -1 \right) } }{ \sqrt { 2\sqrt { 2 } } } \\ \cos { A } =\frac { आधार }{ कर्ण } \\ \cos { A } =\frac { 1 }{ \sqrt { 2\sqrt { 2 } \left( \sqrt { 2 } -1 \right) } } \\ \Rightarrow \sin { A } \cos { A } =\frac { \sqrt { \left( \sqrt { 2 } -1 \right) } }{ \sqrt { 2\sqrt { 2 } } } .\frac { 1 }{ \sqrt { 2\sqrt { 2 } \left( \sqrt { 2 } -1 \right) } } \\ \Rightarrow \sin { A } \cos { A } =\frac { 1 }{ 2\sqrt { 2 } }
- उपर्युक्त उदाहरण के द्वारा न्यून कोणों के त्रिकोणमितीय अनुपात (Trigonometric Ratios of Acute Angle) को समझ सकते हैं।
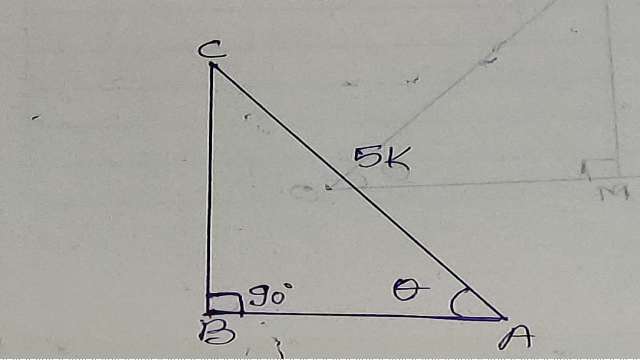
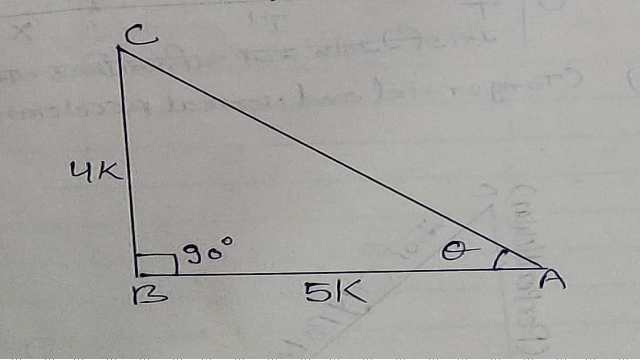
Example-3. यदि \sin { A } =\frac { 1 }{ 3 } हो तो \cos { A } cosecA+\tan { A } \sec { A } का मान ज्ञात कीजिए।
Solution-\sin { A } =\frac { 1 }{ 3 }
त्रिभुज ABC की रचना करते हैं जिसमें लम्ब BC और कर्ण AC; 1:3 के अनुपात में है।
माना AC=3k,BC=k
जहां k>0, जो कि अनुपातिक अचर राशि है।
अतः बौधायन सूत्र से-
{ AB }^{ 2 }={ AC }^{ 2 }-{ BC }^{ 2 }\\ \Rightarrow { AB }^{ 2 }={ \left( 3k \right) }^{ 2 }-{ \left( k \right) }^{ 2 }\\ \Rightarrow { AB }^{ 2 }=9{ k }^{ 2 }-{ k }^{ 2 }=8{ k }^{ 2 }\\ \Rightarrow AB=\pm 2\sqrt { 2 } k
क्योंकि कोण A न्यून कोण है, अतः धनात्मक राशि होगी।
AB=2\sqrt { 2 } k\\ \cos { A } =\frac { AB }{ AC } =\frac { 2\sqrt { 2 } k }{ 3k } \\ \Rightarrow \cos { A } =\frac { 2\sqrt { 2 } }{ 3 } \\ cosecA=\frac { AC }{ BC } \\ \Rightarrow cosecA=\frac { 3k }{ k } \\ \Rightarrow cosecA=3\\ \tan { A } =\frac { BC }{ AB } \\ \Rightarrow \tan { A } =\frac { k }{ 2\sqrt { 2 } k } \\ \Rightarrow \tan { A } =\frac { 1 }{ 2\sqrt { 2 } } \\ \sec { A } =\frac { AC }{ AB } \\ \Rightarrow \sec { A } =\frac { 3k }{ 2\sqrt { 2 } k } \\ \Rightarrow \sec { A } =\frac { 3 }{ 2\sqrt { 2 } } \\ \cos { A } cosecA+\tan { A } \sec { A } \\ \Rightarrow \left( \frac { 2\sqrt { 2 } }{ 3 } \right) \left( 3 \right) +\left( \frac { 1 }{ 2\sqrt { 2 } } \right) \left( \frac { 3 }{ 2\sqrt { 2 } } \right) \\ \Rightarrow 2\sqrt { 2 } +\frac { 3 }{ 8 } \\ \Rightarrow \frac { 16\sqrt { 2 } +3 }{ 8 }
Example-4.यदि 5\tan { \theta } =4 हो तो \frac { 5\sin { \theta } -3\cos { \theta } }{ \sin { \theta } +2\cos { \theta } } का मान ज्ञात कीजिए।
Solution- 5\tan { \theta } =4\Rightarrow \tan { \theta } =\frac { 4 }{ 5 }
त्रिभुज ABC की रचना करते हैं जिसमें अर्थात् लम्ब BC और आधार AB ,4:5 के अनुपात में है।
माना BC=4k,AB=5k
जहां k>0,जो कि अनुपातिक अचर राशि है।
अतः बौधायन सूत्र से-
{ AC }^{ 2 }={ AB }^{ 2 }+{ BC }^{ 2 }\\ \Rightarrow { AC }^{ 2 }={ \left( 5k \right) }^{ 2 }+{ \left( 4k \right) }^{ 2 }\\ \Rightarrow { AC }^{ 2 }=25{ k }^{ 2 }+16{ k }^{ 2 }\\ \Rightarrow { AC }^{ 2 }=41{ k }^{ 2 }\\ \Rightarrow AC=\pm \sqrt { 41 } k
कोण न्यून कोण ऐ, अतः AC धनात्मक होगी।
sin{ \theta }=\frac { BC }{ AC } \\ \Rightarrow sin{ \theta }=\frac { 4k }{ \sqrt { 41 } k } \\ \Rightarrow sin{ \theta }=\frac { 4 }{ \sqrt { 41 } } \\ \cos { \theta } =\frac { AB }{ AC } \\ \Rightarrow \cos { \theta } =\frac { 5k }{ \sqrt { 41 } k } \\ \Rightarrow \cos { \theta } =\frac { 5 }{ \sqrt { 41 } } \\ \frac { 5\sin { \theta } -3\cos { \theta } }{ \sin { \theta } +2\cos { \theta } } \\ \Rightarrow \frac { 5\left( \frac { 4 }{ \sqrt { 41 } } \right) -3\left( \frac { 5 }{ \sqrt { 41 } } \right) }{ \left( \frac { 4 }{ \sqrt { 41 } } \right) +2\left( \frac { 5 }{ \sqrt { 41 } } \right) } \\ \Rightarrow \frac { \frac { 20-15 }{ \sqrt { 41 } } }{ \frac { 4+10 }{ \sqrt { 41 } } } \\ \Rightarrow \frac { 5 }{ 14 }
- उपर्युक्त उदाहरण के द्वारा न्यून कोणों के त्रिकोणमितीय अनुपात (Trigonometric Ratios of Acute Angle) को समझ सकते हैं।
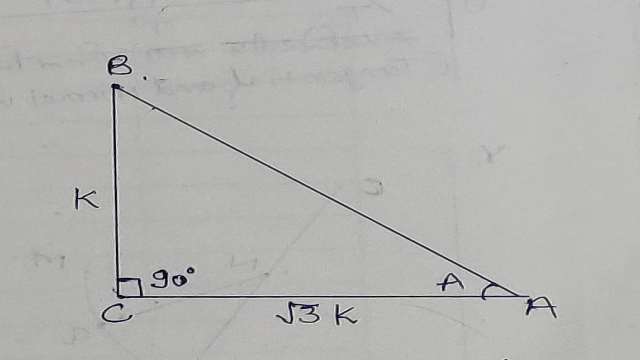
Example-5. त्रिभुज ABC में \angle C={ 90 }^{ 0 } है और यदि \cot { A } =\sqrt { 3 } तथा \cot { B } =\frac { 1 }{ \sqrt { 3 } } है तो सिद्ध कीजिए कि
\sin { A } \cos { B } +\cos { A } \sin { B } =1
Solution-\cot { A } =\frac { \sqrt { 3 } }{ 1 }
त्रिभुज ABC की रचना करते हैं जिसमें आधार AC और लम्ब BC, \sqrt { 3 } :1 के अनुपात में है।
माना AC=\sqrt { 3 } k,BC=k
जहां k>0,जो कि अनुपातिक अचर राशि है।
अतः बौधायन सूत्र से-
{ AB }^{ 2 }={ AC }^{ 2 }+{ BC }^{ 2 }\\ \Rightarrow { AB }^{ 2 }={ \left( \sqrt { 3 } k \right) }^{ 2 }+{ \left( k \right) }^{ 2 }\\ \Rightarrow { AB }^{ 2 }=3{ k }^{ 2 }+{ k }^{ 2 }\\ \Rightarrow { AB }^{ 2 }=4{ k }^{ 2 }\\ \Rightarrow AB=\pm 2k
क्योंकि कोण A न्यून कोण है अतः AB धनात्मक होगी।
AB=2k
\sin { A } =\frac { BC }{ AB } \\ \sin { A } =\frac { k }{ 2k } \\ \Rightarrow \sin { A } =\frac { 1 }{ 2 } \\ \cos { A } =\frac { AC }{ AB } \\ \cos { A } =\frac { \sqrt { 3 } k }{ 2k } \\ \Rightarrow \cos { A } =\frac { \sqrt { 3 } }{ 2 } \\ \sin { B } =\frac { AC }{ AB } \\ \sin { B } =\frac { \sqrt { 3 } k }{ 2k } \\ \Rightarrow \sin { B } =\frac { \sqrt { 3 } }{ 2 } \\ \cos { B } =\frac { BC }{ AB } \\ \cos { B } =\frac { k }{ 2k } \\ \Rightarrow \cos { B } =\frac { 1 }{ 2 } \\ \sin { A } \cos { B } +\cos { A } \sin { B } \\ \left( \frac { 1 }{ 2 } \right) \left( \frac { 1 }{ 2 } \right) +\left( \frac { \sqrt { 3 } }{ 2 } \right) \left( \frac { \sqrt { 3 } }{ 2 } \right) \\ \frac { 1 }{ 4 } +\frac { 3 }{ 4 } =\frac { 1+3 }{ 4 } \\ =\frac { 4 }{ 4 } =1\\ \Rightarrow \sin { A } \cos { B } +\cos { A } \sin { B } =1
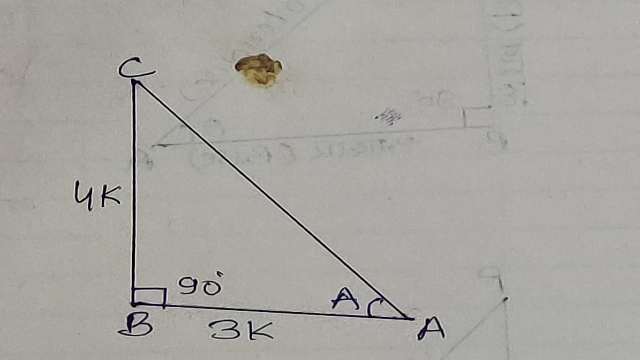
Example-6. यदि 16\cot { A } =12 हो तो \frac { \sin { A } +\cos { A } }{ \sin { A } -\cos { A } } का मान ज्ञात कीजिए।
Solution-16\cot { A } =12\\ \Rightarrow \cot { A } =\frac { 12 }{ 16 } \\ \Rightarrow \cot { A } =\frac { 3 }{ 4 }
त्रिभुज ABC की रचना करते हैं जिसमें आधार AB और लम्ब BC,3:4 के अनुपात में है।
माना AB=3k,BC=4k
जहां k>0,जो कि अनुपातिक अचर राशि है।
अतः बौधायन सूत्र से-
{ AC }^{ 2 }={ AB }^{ 2 }+{ BC }^{ 2 }\\ { AC }^{ 2 }={ \left( 3k \right) }^{ 2 }+{ \left( 4k \right) }^{ 2 }\\ { AC }^{ 2 }=9{ k }^{ 2 }+16{ k }^{ 2 }\\ { AC }^{ 2 }=25{ k }^{ 2 }\\ AC=\pm 5k
क्योंकि A न्यून कोण है अतः AC धनात्मक होगी।
\sin { A } =\frac { BC }{ AC } \\ \Rightarrow \sin { A } =\frac { 4k }{ 5k } \\ \Rightarrow \sin { A } =\frac { 4 }{ 5 } \\ \cos { A } =\frac { AC }{ AB } \\ \Rightarrow \cos { A } =\frac { 3k }{ 5k } \\ \Rightarrow \cos { A } =\frac { 3 }{ 5 } \\ \Rightarrow \frac { \sin { A } +\cos { A } }{ \sin { A } -\cos { A } } =\frac { \frac { 4 }{ 5 } +\frac { 3 }{ 5 } }{ \frac { 4 }{ 5 } -\frac { 3 }{ 5 } } =\frac { \frac { 7 }{ 5 } }{ \frac { 1 }{ 5 } } =7\\ \Rightarrow \frac { \sin { A } +\cos { A } }{ \sin { A } -\cos { A } } =7
- उपर्युक्त उदाहरण के द्वारा न्यून कोणों के त्रिकोणमितीय अनुपात (Trigonometric Ratios of Acute Angle) को समझ सकते हैं।
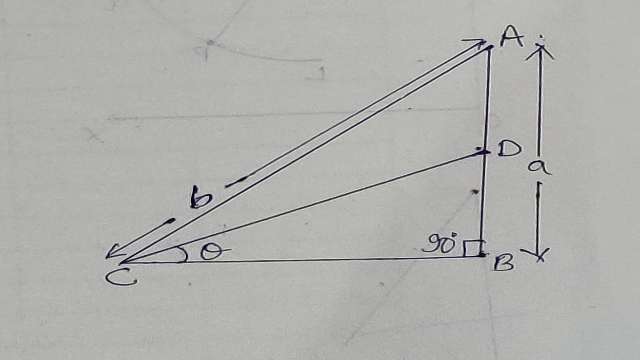
Example-7. चित्र में AD=DB तथा \angle B={ 90 }^{ \circ } तो निम्नलिखित के मान ज्ञात कीजिए-
(i)\sin { \theta } \quad (ii)\cos { \theta } \quad (iii)\tan { \theta }
Solution- AB=a
AD=DB=\frac { a }{ 2 }
बौधायन सूत्र से त्रिभुज ABC में
{ AC }^{ 2 }={ AB }^{ 2 }+{ BC }^{ 2 }\\ \Rightarrow { BC }^{ 2 }={ AC }^{ 2 }-{ AB }^{ 2 }\\ \Rightarrow { BC }^{ 2 }={ b }^{ 2 }-{ a }^{ 2 }\\ \Rightarrow BC=\sqrt { { b }^{ 2 }-{ a }^{ 2 } }
समकोण त्रिभुज BCD में बौधायन सूत्र से-
{ DC }^{ 2 }={ BC }^{ 2 }+{ BD }^{ 2 }\\ \Rightarrow { DC }^{ 2 }={ b }^{ 2 }-{ a }^{ 2 }+{ (\frac { a }{ 2 } ) }^{ 2 }\\ \Rightarrow { DC }^{ 2 }={ b }^{ 2 }-{ a }^{ 2 }+\frac { { a }^{ 2 } }{ 4 } \\ \Rightarrow { DC }^{ 2 }={ b }^{ 2 }+\frac { { a }^{ 2 }-4{ a }^{ 2 } }{ 4 } \\ \Rightarrow { DC }^{ 2 }={ b }^{ 2 }-\frac { 3{ a }^{ 2 } }{ 4 } \\ \Rightarrow { DC }^{ 2 }=\frac { 4{ b }^{ 2 }-3{ a }^{ 2 } }{ 4 } \\ \Rightarrow { DC }=\frac { \sqrt { 4{ b }^{ 2 }-3{ a }^{ 2 } } }{ 2 } \\ (i)\sin { \theta } =\frac { BD }{ CD } \\ \Rightarrow \sin { \theta } =\frac { \frac { a }{ 2 } }{ \frac { \sqrt { 4{ b }^{ 2 }-3{ a }^{ 2 } } }{ 2 } } \\ \Rightarrow \sin { \theta } =\frac { a }{ \sqrt { 4{ b }^{ 2 }-3{ a }^{ 2 } } } \\ (ii)\cos { \theta } =\frac { BC }{ CD } \\ \Rightarrow \cos { \theta } =\frac { \sqrt { { b }^{ 2 }-{ a }^{ 2 } } }{ \frac { \sqrt { 4{ b }^{ 2 }-3{ a }^{ 2 } } }{ 2 } } \\ \Rightarrow \cos { \theta } =\frac { 2\sqrt { { b }^{ 2 }-{ a }^{ 2 } } }{ \sqrt { 4{ b }^{ 2 }-3{ a }^{ 2 } } } \\ (iii)\tan { \theta } =\frac { BD }{ BC } \\ \Rightarrow \tan { \theta } =\frac { \frac { a }{ 2 } }{ \sqrt { { b }^{ 2 }-{ a }^{ 2 } } } \\ \Rightarrow \tan { \theta } =\frac { a }{ 2\sqrt { { b }^{ 2 }-{ a }^{ 2 } } }
Example-8. यदि \cos { \theta } =\frac { 3 }{ 5 } हो तो \frac { \sin { \theta } -\cot { \theta } }{ \tan { \theta } } का मान ज्ञात कीजिए।
Solution-\cos { \theta } =\frac { 3 }{ 5 }
त्रिभुज ABC की रचना करते हैं जिसमें आधार AB और लम्ब BC ,3:5 के अनुपात में है।
माना AB=3k,AC=5k
जहां k>0,जो कि अनुपातिक अचर राशि है।
अतः बौधायन सूत्र से-
{ AC }^{ 2 }={ AB }^{ 2 }+{ BC }^{ 2 }\\ \Rightarrow { BC }^{ 2 }={ AC }^{ 2 }-{ AB }^{ 2 }\\ \Rightarrow { BC }^{ 2 }={ \left( 5k \right) }^{ 2 }-{ \left( 3k \right) }^{ 2 }\\ \Rightarrow { BC }^{ 2 }=25{ k }^{ 2 }-9{ k }^{ 2 }\\ \Rightarrow { BC }^{ 2 }=16{ k }^{ 2 }\\ \Rightarrow BC=\pm 4k
क्योंकि न्यून कोण है अतः BC धनात्मक होगी।
\sin { \theta } =\frac { BC }{ AB } \\ \Rightarrow \sin { \theta } =\frac { 4k }{ 5k } \\ \Rightarrow \sin { \theta } =\frac { 4 }{ 5 } \\ \cot { \theta } =\frac { AB }{ BC } \\ \Rightarrow \cot { \theta } =\frac { 3k }{ 4k } \\ \Rightarrow \cot { \theta } =\frac { 3 }{ 4 } \\ \tan { \theta } =\frac { BC }{ AB } \\ \Rightarrow \tan { \theta } =\frac { 4k }{ 3k } \\ \Rightarrow \tan { \theta } =\frac { 4 }{ 3 } \\ \frac { \sin { \theta } -\cot { \theta } }{ 2\tan { \theta } } \\ \Rightarrow \frac { \frac { 4 }{ 5 } -\frac { 3 }{ 4 } }{ 2\times \frac { 4 }{ 3 } } \\ \Rightarrow \frac { \frac { 16-15 }{ 20 } }{ \frac { 8 }{ 3 } } \\ \Rightarrow \frac { 1 }{ 20 } \times \frac { 3 }{ 8 } \\ \Rightarrow \frac { 3 }{ 160 }
उपर्युक्त उदाहरणों के द्वारा न्यून कोणों के त्रिकोणमितीय अनुपात (Trigonometric Ratios of Acute Angle) को समझ सकते हैं।
3.न्यून कोणों के त्रिकोणमितीय अनुपात की समस्याएं (Trigonometric Ratios of Acute Angle Problems)-
- (1.)यदि \triangle ABC में \angle B={ 90 }^{ \circ },a=12 सेमी,b=13 सेमी हो तो कोण \angle A और \angle C के लिए सभी त्रिकोणमितीय अनुपात लिखिए।
(2.)यदि \cos { \theta } =\frac { 8 }{ 17 } हो तो शेष त्रिकोणमितीय अनुपात ज्ञात कीजिए।
(3.)यदि \cos { A } =\frac { 5 }{ 13 } हो तो \frac { cosecA }{ \cos { A } +cosecA } का मान ज्ञात कीजिए।
(4.)यदि \cos { \theta } =\frac { 21 }{ 29 } हो तो \frac { \sec { \theta } }{ \tan { \theta } -\sin { \theta } } का मान ज्ञात कीजिए।
(5.)यदि \cot { A } =\sqrt { 3 } हो तो सिद्ध कीजिए कि \sin { A } \cos { B } +\cos { A } \sin { B } =1
(6.)यदि \sec { \theta } =\frac { 13 }{ 12 } हो तो \frac { 1-\tan { \theta } }{ 1+\tan { \theta } } का मान ज्ञात कीजिए। - उत्तर-(1)\sin { A } =\frac { 12 }{ 13 } ,\cos { A } =\frac { 5 }{ 13 } ,\tan { A } =\frac { 12 }{ 5 } ,cosecA=\frac { 13 }{ 12 } \\ \sec { A } =\frac { 13 }{ 5 } ,\cot { A } =\frac { 5 }{ 12 } \\ \sin { C } =\frac { 5 }{ 13 } ,\cos { C } =\frac { 12 }{ 13 } ,\tan { C } =\frac { 5 }{ 12 } ,cosecC=\frac { 13 }{ 5 } ,\sec { C } =\frac { 13 }{ 12 } \\ \cot { C } =\frac { 12 }{ 5 } \\ (2)\sin { \theta } =\frac { 15 }{ 17 } ,\tan { \theta } =\frac { 15 }{ 8 } ,cosec\theta =\frac { 17 }{ 15 } \\ \sec { \theta } =\frac { 17 }{ 8 } ,\cot { \theta } =\frac { 8 }{ 15 } \\ (3)\frac { 169 }{ 229 } \\ (4)\frac { 841 }{ 160 } \\ (6)\frac { 7 }{ 17 }
- उपर्युक्त सवालों को हल करने पर न्यून कोणों के त्रिकोणमितीय अनुपात (Trigonometric Ratios of Acute Angle) ठीक से समझ में आ सकता है।
4.आप एक कोण के त्रिकोणमितीय अनुपात को कैसे ज्ञात करते हैं? (How do you find the trigonometric ratio of an angle?)-
- हम सीखेंगे कि निम्न चरण-दर-चरण प्रक्रिया का उपयोग करके किसी भी कोण के त्रिकोणमितीय अनुपात कैसे खोजें।
चरण I: कोणों के त्रिकोणमितीय अनुपात (n ± 90 ° ± the) को खोजने के लिए;जहां n एक पूर्णांक है और θ एक धनात्मक न्यून कोण है,हम नीचे दी गई प्रक्रिया का पालन करेंगे। - पहले हमें दिए गए त्रिकोणमितीय अनुपात के संकेत को निर्धारित करने की आवश्यकता है।अब दिए गए त्रिकोणमितीय अनुपात के चिन्ह को निर्धारित करने के लिए हमें चतुर्थांश को खोजने की आवश्यकता है जिसमें कोण (n .90 ° + θ) या (n.90 °- θ) स्थित है।
- अब, नियम “ऑल, sin, tan,cos” का उपयोग करते हुए हम दिए गए त्रिकोणमितीय अनुपात का चिन्ह पाएंगे।
- (i) सभी त्रिकोणमितीय अनुपात धनात्मक हैं यदि दिए गए कोण (n . 90 ° + θ) या (n .90 ° + θ) प्रथम चतुर्थांश (पहला चतुर्थांश) में निहित है;
- (ii) केवल sin और csc अनुपात धनात्मक है यदि दिए गए कोण (n .90 ° + θ) या (n .90 ° – θ) II चतुर्थांश (दूसरा चतुर्थांश) में निहित है;
- (iii) केवल tan और cot अनुपात धनात्मक है यदि दिए गए कोण (n . 90 ° + θ) या (n .90 °- θ) III चतुर्थांश (तृतीय चतुर्थांश) में निहित है;
- (iv) केवल cos और sec अनुपात धनात्मक है यदि दिए गए कोण (n . 90 ° + θ) या (n .90 °- θ) IV चतुर्थांश (चतुर्थांश) में निहित है।
5.एक न्यून कोण के लिए सूत्र क्या है? (What is the formula for an acute angle?)-
- एक समकोण त्रिभुज किसी भी त्रिभुज को संदर्भित करता है जिसमें 90 डिग्री या समकोण होता है।इसके अलावा, किसी भी त्रिभुज में कोण कुल 180 डिग्री होना चाहिए। यह निश्चित रूप से इसका मतलब है कि अन्य दो कोण न्यून कोण हैं।
- त्रिकोणमिति मुख्य रूप से सही त्रिकोण के माप और अनुपात से सम्बन्धित है।एक सही त्रिभुज के न्यून कोणों पर अधिकांश उल्लेखनीय, साइन, कोसाइन और टेन्जेन्ट केंद्र। इसलिए, कोणों की गणना करने के लिए इन अनुपातों का उपयोग करना चाहिए।
- एक व्यक्ति को त्रिभुज को इस तरह उन्मुख करना चाहिए कि समकोण की एक भुजा लंबवत हो जाए।इसके अलावा, व्यक्ति को इस भुजा को “a” के रूप में लेबल करना चाहिए।
- समकोण का दूसरी भुजा क्षैतिज होगी।व्यक्ति को इस भुजा को “b” के रूप में लेबल करना चाहिए।तीसरा पक्ष जो कर्ण है उसे “c” लेबल किया जाना चाहिए।
- व्यक्ति को तीन पक्षों की लंबाई मापनी चाहिए।इसके अलावा, वहाँ मौजूद अनुप्रयोग हैं, जो पक्षों की माप “a” और “b” की अनुमति देते हैं।ऐसे मामले में, व्यक्ति को “c” पक्ष की गणना के लिए पाइथागोरस प्रमेय का उपयोग करना चाहिए।
- व्यक्ति को “c” कर्ण की लंबाई के साथ “a” पक्ष की लंबाई को विभाजित करना चाहिए।यह निश्चित रूप से न्यून कोण की sin है जो क्षैतिज भुजा को समकोण के साथ साझा करता है।
- इसके अलावा, व्यक्ति को वैज्ञानिक कैलकुलेटर में इस अनुपात को दर्ज करना होगा।फिर व्यक्ति को कोण के निर्धारण के लिए प्रतिलोम साइन फ़ंक्शन का उपयोग करना चाहिए।
- व्यक्ति को इस कोण पर 90 डिग्री दर्ज करना होगा।इसके अलावा, व्यक्ति को परिणाम को 180 से घटाना होगा।अंत में, यह सही त्रिकोण में मौजूद दूसरे न्यून कोण का मान होगा।
6.आप एक न्यून कोण के त्रिकोणमितीय फ़ंक्शन को कैसे ज्ञात करते हैं? (How do you find the trigonometric function of an acute angle?),6 त्रिकोणमितीय अनुपात क्या हैं? (What are the 6 trigonometric ratios?),समकोण त्रिभुज के न्यून कोण के त्रिकोणमितीय अनुपात (Trigonometric ratios of an acute angle of a right-angled triangle)-
\sin { \theta } =\frac { 1 }{ cosec\theta } \\ \cos { \theta } =\frac { 1 }{ \sec { \theta } } \\ \tan { \theta } =\frac { \sin { \theta } }{ \cos { \theta } } \\ \tan { \theta } =\frac { 1 }{ \cot { \theta } } \\ \cot { \theta } =\frac { \cos { \theta } }{ \sin { \theta } } \\ \cot { \theta } =\frac { 1 }{ \tan { \theta } } \\ \sec { \theta } =\frac { 1 }{ \cos { \theta } } \\ \cos { \theta } =\frac { 1 }{ \sec { \theta } } \\ cosec\theta =\frac { 1 }{ \sin { \theta } } \\ \sin ^{ 2 }{ \theta } +\cos ^{ 2 }{ \theta } =1\\ 1+\tan ^{ 2 }{ \theta } =\sec ^{ 2 }{ \theta } \\ 1+\cot ^{ 2 }{ \theta } ={ cosec }^{ 2 }\theta \\ \sin { (90-\theta ) } =\cos { \theta } \\ \cos { (90-\theta ) } =\sin { \theta } \\ \tan { (90-\theta ) } =\cot { \theta } \\ \cot { (90-\theta ) } =\tan { \theta } \\ \sec { (90-\theta ) } =cosec\theta \\ cosec(90-\theta )=\sec { \theta }7.निम्नलिखितक कोणों को न्यून कोणों के त्रिकोणमितीय अनुपात के पदों में व्यक्त करो (Express the following in terms of trigonometric ratios of acute angles)-
- (i) sin 1185° (ii) tan 235° (iii) sin (- 3333)
(iv) cot (-3888°) (v) tan 458°(vi) cosec (-60°)
(vii) cos 500° (viii) sec 380° - Answer:Step-by-step explanation:
(i) sin 1185° = Sin( 1080 + 105)° = Sin(3 * 360 + 105)° = Sin105°
= Sin(90 + 15)° = Cos 15°
(ii) tan 235° = Tan (180 + 55)° = Tan 55°
(iii) sin (- 3333°) = – Sin(3333°) = -Sin(3240 + 93)° = -Sin(360 *9 + 93)°= – Sin93° = – Sin(90 + 3)° = – (Cos3°) = -Cos3°
(iv) cot (-3888°) = – Cot(3888°) = -Cot(3600 + 288)° = -Cot 288° = -Cot(180 + 108)° = -Cot108° = -Cot(90 + 18°) = -(-Tan18°) = Tan18°
(v) tan 458° = Tan (360 + 98)° = Tan 98° = Tan (90 + 8)° = -Cot8°
(iv) cosec (-60°) = -Cosec60°
(vii) cos 500° = Cos (360 + 140)° = Cos 140° = Cos(180 – 40)° = -Cos40°
(viii) sec 380° = Sec(360 + 20)° = Sec 20°
Also Read This Article:-Algebraic identities
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
