Theorem of Parallel Axes in Dynamics
1.गतिविज्ञान में समान्तर अक्षों का प्रमेय (Theorem of Parallel Axes in Dynamics),जड़त्व-आघूर्ण एवं गुणन के लिए समान्तर अक्षों का प्रमेय (Theorem of Parallel Axes for Moment and Product of Inertia):
गतिविज्ञान में समान्तर अक्षों का प्रमेय (Theorem of Parallel Axes in Dynamics) तथा लम्बवत अक्षों का प्रमेय पर आधारित विशिष्ट सवालों को हल करके समझने का प्रयास करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Moment of Inertia in Dynamics
2.गतिविज्ञान में समान्तर अक्षों का प्रमेय के उदाहरण (Theorem of Parallel Axes in Dynamics Examples):
Example:1.एक M द्रव्यमान एवं r त्रिज्या की वृत्तीय चकती का
(Find the M. I. of a circular disc of mass M and radius r)
Example:1(i).स्वयं की अक्ष के समान्तर एक स्पर्श रेखीय अक्ष के सापेक्ष
(about tangent parallel to its axis.)
Solution:समान्तर अक्षों की प्रमेय के अनुसार वृत्तीय चकती स्वयं की अक्ष के समान्तर स्पर्श रेखीय अक्ष के सापेक्ष जड़त्व-आघूर्ण=वृत्तीय चकती का अक्ष के परितः जड़त्व-आघूर्ण+वृत्तीय चकती की संहति को गुरुत्व केन्द्र पर स्थापन कर स्पर्श रेखा के परितः जड़त्व-आघूर्ण =\frac{1}{2} M r^2+M r^2 \\ =\frac{3}{2} M r^2
Example:1(ii).इसके व्यास के समान्तर एक स्पर्शरेखीय अक्ष के सापेक्ष
(About tangent parallel to its diameter.)
Solution:समान्तर अक्षों की प्रमेय के अनुसार वृत्तीय चकती का स्पर्श रेखा के परितः जड़त्व-आघूर्ण=वृत्तीय चकती का व्यास के परितः जड़त्व-आघूर्ण+वृत्तीय चकती की संहति को गुरुत्व केन्द्र पर स्थापन कर स्पर्श रेखा के परितः जड़त्व-आघूर्ण=\frac{1}{4} M r^2+M r^2 \\ =\frac{5}{4} M r^2
Example:1(iii).चकती के तल में इसके केन्द्र से c लम्बवत दूरी पर एक रेखा के सापेक्ष,जड़त्व-आघूर्ण ज्ञात करो।
(About a line in its own plane whose perpendicular distance from its centre is c.)
Solution:दी हुई रेखा के समान्तर व्यास के परितः जड़त्व-आघूर्ण=\frac{1}{4} M r^2
अतः दी हुई रेखा के परितः जड़त्व-आघूर्ण=\frac{1}{4} M r^2+M c^2 \\ =M\left(c^2+\frac{1}{4} r^2\right)
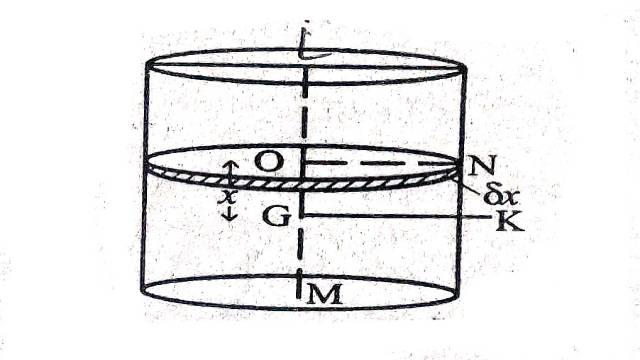
Example:2.सिद्ध कीजिए कि एक खोखले बेलन तथा ठोस बेलन का गुरुत्व केन्द्र से गुजरने वाले तथा अक्ष के लम्बवत तल में स्पर्श रेखा के परितः जड़त्व-आघूर्ण क्रमशः M\left(\frac{3 a^2}{2}+\frac{h^2}{3}\right) तथा \left(\frac{5 a^2}{4}+\frac{b^2}{3}\right) हैं।जहाँ आधार की त्रिज्या a तथा बेलन की ऊँचाई 2h है।
(Show that the moment of inertia of a hollow cylinder and solid cylinder about a tangent in the plane passing through C. G. and perpendicular axis are respectively M\left(\frac{3 a^2}{2}+\frac{h^2}{3}\right) and \left(\frac{5 a^2}{4}+\frac{b^2}{3}\right), where a is the radius of the base and height of the cylinder is 2h.)
Solution:लम्बवृत्तीय बेलन की ऊँचाई 2h है।
एक पतली चक्रिका गुरुत्व केन्द्र G से x दूरी पर तथा मान लो कि चक्रिका की मोटाई \delta x है।
अवयव चक्रिका की संहति=\pi a^2 \delta x \rho
जहाँ \rho बेलन का घनत्व है।
M=\int_{-h}^h \pi a^2 \rho d x \\ =\pi a^2 \rho[x]_{-h}^h \\ =2 \pi a^2 \rho h \\ \Rightarrow \rho=\frac{M}{2 \pi a^2 h}
खोखले बेलन में अवयव चक्रिका GK के परितः जड़त्व-आघूर्ण=चक्रिका का ON के परितः जड़त्व-आघूर्ण+चक्रिका की संहति को O पर स्थापन कर GK के परितः जड़त्व-आघूर्ण
=\pi a^2 \delta x \rho \cdot \frac{a^2}{2}+\pi a^2 \delta x \rho x^2
अतः खोखले बेलन का GK के परितः जड़त्व-आघूर्ण =\pi a^2 \rho \int_{-h}^h\left(\frac{a^2}{2}+x^2\right) d x \\ =\pi a^2 \cdot \frac{M}{2 \pi a^2 h}\left[\frac{a^2}{2} x+\frac{x^3}{3}\right]_{-h}^h \\ =\frac{M}{2 h}\left[a^2 h+\frac{2 h^3}{3}\right] \\ =M\left[\frac{a^2}{2}+\frac{h^2}{3}\right]
गुरुत्व केन्द्र से गुजरने वाले तथा अक्ष के लम्बवत तल में स्पर्शरेखा के परितः जड़त्व-आघूर्ण=गुरुत्व केन्द्र के परितः जड़त्व-आघूर्ण+G पर M संहति स्थापन कर स्पर्श रेखा के परितः जड़त्व-आघूर्ण
=M\left(\frac{a^2}{2}+\frac{h^2}{3}\right)+M a^2 \\ =M\left(\frac{3}{2} a^2+\frac{h^2}{3}\right)
इसी प्रकार ठोस बेलन का GK के परितः जड़त्व-आघूर्ण
=\pi a^2 \rho \int_{-h}^h\left(\frac{a^2}{4}+x^2\right) d x \\ =\pi a^2 \times \frac{M}{2 \pi a^2 h}\left[\frac{a^2}{4} x+\frac{x^3}{3}\right]_{-h}^h \\ =\frac{M}{2 h}\left[\frac{a^2 h}{2}+\frac{2 h^3}{3}\right] \\ =M\left[\frac{a^2}{4}+\frac{h^2}{3}\right]
अतः गुरुत्व केन्द्र से गुजरने वाले तथा अक्ष के लम्बवत तल में स्पर्शरेखा के परितः जड़त्व-आघूर्ण=गुरुत्व केन्द्र के परितः जड़त्व-आघूर्ण+G पर M संहति स्थापन कर स्पर्शरेखा के परितः जड़त्व-आघूर्ण
=M\left[\frac{a^2}{4}+\frac{h^2}{3}\right]+m a^2 \\ =M\left(\frac{5 a^2}{4}+\frac{h^2}{3}\right)
Example:3.किसी दीर्घवृत्तीय पटल का जड़त्व-आघूर्ण ज्ञात करिये:
(Find the moment of inertia of elliptic lamina about):
Example:3(i).पटल के तल में लघु अक्ष के समान्तर स्पर्शरेखा के सापेक्ष
(the tangent to the lamina, parallel to the minor axis, and in the plane of the lamina),
Solution:पटल के तल में लघुअक्ष के समान्तर स्पर्शरेखा के सापेक्ष जड़त्व-आघूर्ण=लघुअक्ष के परितः जड़त्व-आघूर्ण+दीर्घवृत्तीय पटल को गुरुत्व केन्द्र पर स्थापन कर स्पर्श रेखा के परितः जड़त्व-आघूर्ण
=\frac{1}{4} M a^2+M a^2 \\ =\frac{5}{4} M a^2
Example:3(ii).दीर्घवृत्त के सिरे में से पटल के तल के लम्बवत किसी अक्ष के सापेक्ष
(the axis passing through the end of major axis and perpendicular to the plane of the lamina.)
Solution:पटल के तल के लम्बवत किसी अक्ष के सापेक्ष जड़त्व-आघूर्ण=दीर्घअक्ष के परितः जड़त्व-आघूर्ण+लघुअक्ष के परितः जड़त्व-आघूर्ण
=\frac{1}{4} M\left(a^2+b^2\right)
Example:4.एक समान ठोस गोला जिसकी त्रिज्या a तथा संहति M है,का किसी भी स्पर्शी रेखा के परितः जड़त्व-आघूर्ण ज्ञात करिए।
(Find the M. I. of a uniform solid sphere of radius a, mass about any tangent line.)
Solution:ठोस गोले का व्यास के परितः जड़त्व-आघूर्ण= \frac{2}{5} M a^2
व्यास के समान्तर स्पर्शी के परितः जड़त्व-आघूर्ण=ठोस गोले का व्यास के परितः जड़त्व-आघूर्ण+गुरुत्व केन्द्र पर M संहति स्थापन कर स्पर्शरेखा के परितः जड़त्व-आघूर्ण
=\frac{2}{5} M a^2+M a^2 \\ =\frac{7}{5} M a^2
Example:5.नाभिलम्ब तथा लघुअक्ष के किनारे पर स्पर्शरेखा के सापेक्ष जड़त्व-आघूर्ण बराबर हो तो दीर्घवृत्त की उत्केन्द्रता ज्ञात करिए।
(Find the eccentricity of the ellipse for which the moments of intertia about the tangent at the extremity of minor axis are equal)
Solution:लघुअक्ष के परितः जड़त्व-आघूर्ण =\frac{1}{4} M a^2
तथा लघुअक्ष के किनारे पर स्पर्शरेखा के परितः जड़त्व-आघूर्ण=दीर्घअक्ष के परितः जड़त्व-आघूर्ण+दीर्घवृत्त की संहति M को गुरुत्व केन्द्र पर स्थापन कर स्पर्शरेखा के परितः जड़त्व-आघूर्ण =\frac{1}{4} M b^2+M b^2
नाभिलम्ब के परितः जड़त्व-आघूर्ण=लघुअक्ष के परितः जड़त्व-आघूर्ण+दीर्घवृत्त की संहति M को गुरुत्व केन्द्र पर स्थापन कर नाभिलम्ब के परितः जड़त्व-आघूर्ण=\frac{1}{4} M a^2+M\left(a^2 e^2\right)
प्रश्नानुसार
=\frac{1}{4} M b^2+ M b^2=\frac{1}{4} M a^2+M a^2 e^2 \\ \Rightarrow \frac{5}{4} M b^2=M a^2\left(\frac{1}{4}+e^2\right) \\ \Rightarrow b^2=a^2\left(1-e^2\right) रखने पर
\Rightarrow \frac{5}{4} M a^2\left(1-e^2\right)=m a^2\left(\frac{1}{4}+e^2\right) \\ \Rightarrow \frac{5}{4}\left(1-e^2\right)=\left(\frac{1}{4}+e^2\right) \\ \Rightarrow \frac{5}{4}-\frac{5}{4} e^2=\frac{1}{4}+e^2 \\ \Rightarrow e^2+\frac{5}{4} e^2=\frac{5}{4}-\frac{1}{4} \\ \Rightarrow \frac{9}{4} e^2=1 \\ \Rightarrow e^2=\frac{4}{9} \\ \Rightarrow e=\frac{2}{3}
Example:6.सिद्ध कीजिए कि M संहति तथा 2a,2b भुजा वाले आयताकार पटल का उसके विकर्ण के सापेक्ष जड़त्व-आघूर्ण निम्न है:
\frac{2 M}{3} \cdot \frac{a^2 b^2}{a^2+b^2}
Show that M. I. of rectangle of mass M and side 2a,2b about a diagonal is
\frac{2 M}{3} \cdot \frac{a^2 b^2}{a^2+b^2}
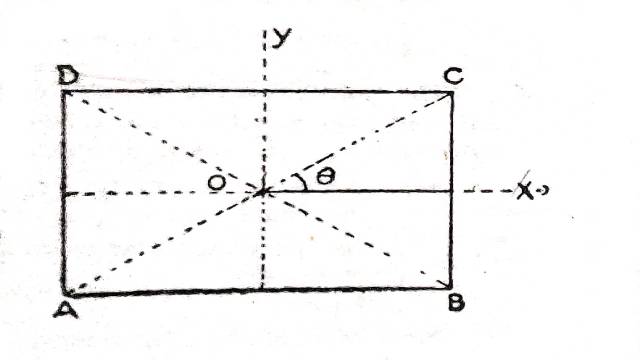
Solution:माना ABCD आयताकार पटल है जिसकी भुजा AB=2a,AD=2b है।
OX के परितः जड़त्व-आघूर्ण=\frac{1}{3} M b^2
OY के परितः जड़त्व-आघूर्ण=\frac{1}{3} M a^2
माना विकर्ण AC,AB के साथ \theta कोण बनाता है तथा
\sin \theta=\frac{b}{\sqrt{a^2+b^2}}, \cos \theta=\frac{a}{\sqrt{a^2+b^2}}
विकर्ण AC के परितः जड़त्व-आघूर्ण
=OX के परितः जड़त्व-आघूर्ण. \cos^2 \theta +OY के परितः जड़त्व-आघूर्ण. \sin^2 \theta +0 (जबकि F=0)
=\frac{1}{3} M b^2 \cos ^2 \theta+\frac{1}{3} M a^2 \sin ^2 \theta \\ =\frac{1}{3} M b^2 \cdot \frac{a^2}{a^2+b^2}+\frac{1}{3} M a^2 \cdot \frac{b^2}{a^2+b^2} \\ =\frac{2 M a^2 b^2}{3\left(a^2 +b^2\right)}
Example:7.सिद्ध कीजिए कि M संहति तथा अर्धांश a तथा b के दीर्घवृत्तीय पटल का उसके केन्द्र से p दूरी पर स्थित किसी स्पर्शरेखा के परितः जड़त्व-आघूर्ण \frac{5}{4} M p^2 है।
(Show that the moment of inertia of an ellipse of mass M and semi-axes a and b about a tangent at a distance p from the centre \frac{5}{4} M p^2.)
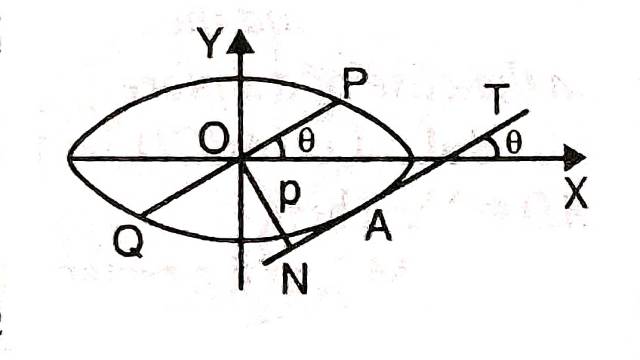
Solution:माना स्पर्शरेखा AT,OX के साथ \theta कोण बनाती है।तब स्पर्शरेखा की समीकरण
y=x \tan \theta+\left(a^2 \tan ^2 \theta+b^2\right)^{\frac{1}{2}} \cdots(1)
p=ON=केन्द्र O(0,0) से स्पर्शरेखा पर लम्ब
=\frac{\left(a^2 \tan ^2 \theta+b^2\right)^{\frac{1}{2}}}{\left(1+\tan ^2 \theta\right)^{\frac{1}{2}}} \\ p=\left(a^2 \sin ^2 \theta+b^2 \cos ^2 \theta\right)^{\frac{1}{2}}
माना PQ दीर्घवृत्त का व्यास है,जो (1) के समान्तर है
I=PQ के परितः जड़त्व-आघूर्ण
=\frac{M}{4}\left(b^2 \cos ^2 \theta+a^2 \sin ^2 \theta\right) \\ \Rightarrow I=\frac{1}{4} M p^2 [(2) से]
अतः समान्तर अक्षों के प्रमेय से,स्पर्शरेखा AT के परितः जड़त्व-आघूर्ण=PQ के परितः जड़त्व-आघूर्ण+दीर्घवृत्त की संहति M को गुरुत्व केन्द्र O पर स्थापन कर स्पर्शरेखा AT के परितः जड़त्व-आघूर्ण
=\frac{4}{4} M P^2+M \times(O N)^2 \\ =\frac{1}{4} M P^2+M P^2 \\ =\frac{5}{4} M p^2
Example:8.यदि दीर्घवृत्तीय पटल के दो संयुग्मी व्यास के परितः घूर्णन त्रिज्या k_1, k_2 है,तब सिद्ध कीजिए कि \frac{1}{k_1^2}+\frac{1}{k_2^2}=4\left(\frac{1}{a^2}+\frac{1}{b^2}\right) जहाँ दीर्घवृत्त के अर्धांक्ष a तथा b है।
(If k_1, k_2 the radii of gyration of an elliptic lamina about two conjugate diameters,then prove that \frac{1}{k_1^2}+\frac{1}{k_2^2}=4\left(\frac{1}{a^2}+\frac{1}{b^2}\right))
Solution:दीर्घअक्ष OX के परितः जड़त्व-आघूर्ण=\frac{1}{4} M b^2=A
लघुअक्ष OY के परितः जड़त्व-आघूर्ण=\frac{1}{4} M a^2=B
इन अक्षों के परितः जड़त्व गुणन=0
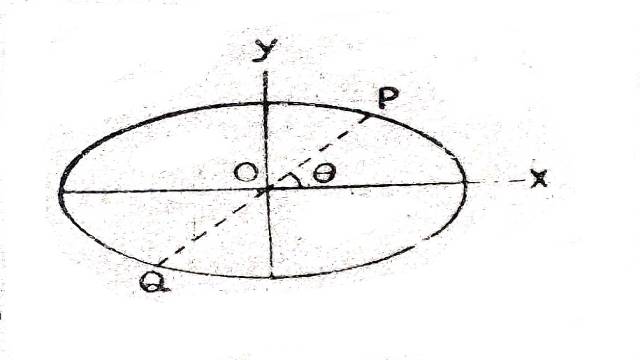
माना PQ व्यास है जो OX के साथ \theta कोण बनाता है।P के निर्देशांक ( r \cos \theta, r \sin \theta)
P दीर्घवृत्त \frac{x^2}{a^2}+\frac{y^2}{b^2} पर स्थित है अतः
\frac{r^2}{a^2} \cos ^2 \theta+\frac{r^2}{b^2} \sin ^2 \theta=1 \\ \Rightarrow \frac{a^2 b^2}{r^2}=b^2 \cos ^2 \theta+a^2 \sin ^2 \theta \cdots(1)
PQ के परितः जड़त्व-आघूर्ण
=A \cos ^2 \theta+B \sin \theta \\ =\frac{1}{4} M b^2 a \cos ^2 \theta+\frac{1}{4} M a^2 \sin \theta \\ =\frac{1}{4} M\left(b^2 \cos ^2 \theta+a^2 \sin ^2 \theta\right)=\frac{1}{4} M \frac{a^2 b^2}{r^2} [(1) से]
यदि CP तथा CD दो संयुग्मी अर्द्धव्यास r_{1} तथा r_{2} लम्बाई के हों तो
M k_1^2 =\frac{M}{4} \cdot \frac{a^2 b^2}{r_1^2}
तथा M k_2^2 =\frac{M}{4} \cdot \frac{a^2 b^2}{r_2^2} \\ \Rightarrow \frac{1}{k_1^2}+\frac{1}{k_2^2} =\frac{4 r_1^2}{a^2 b^2}+\frac{4 r_2^2}{a^2 b^2} \\ =\frac{4}{a^2 b^2}\left(r_1^2+r_2^2\right) \\ =\frac{4}{a^2 b^2}\left(a^2+b^2\right) \\ \Rightarrow \frac{1}{k_1^2}+\frac{1}{k_2^2} =4 \left(\frac{1}{a^2}+\frac{1}{b^2}\right)
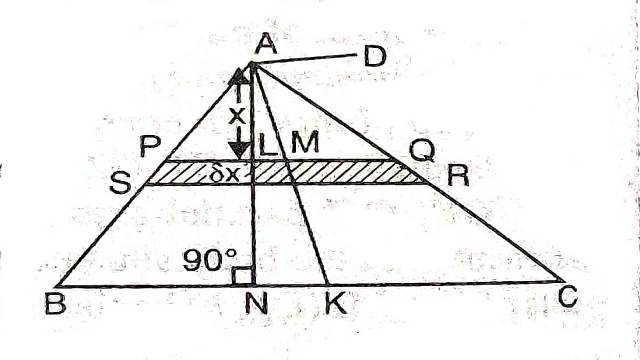
Example:9.एक त्रिभुज ABC का A से गुजरनेवाली तथा त्रिभुज के समतल के लम्बवत रेखा के परितः जड़त्व-आघूर्ण ज्ञात करिए।
(Find the M. I. of a triangle ABC about a line perpendicular to its plane through A.)
Solution:माना त्रिभुज पटल ABC का द्रव्यमान M तथा ऊँचाई h(=AN) है।BC के समान्तर पट्टिका PQRS है जिसकी चौड़ाई \delta x है जो शीर्ष A से AL (=x) दूरी पर है।माना BC=a
\triangle A B C \sim \triangle A P Q \\ \frac{x}{A N}=\frac{PQ}{BC} \\ \Rightarrow \frac{x}{h}=\frac{PQ}{a} \\ \Rightarrow P Q=\frac{ax}{h} \\ \rho=\triangle ABC के प्रति क्षेत्रफल इकाई का द्रव्यमान
=\frac{M}{\frac{1}{2} h a}=\frac{2 M}{h a}
पट्टिका का द्रव्यमान =\delta M=\rho \cdot PQ \cdot \delta x \\ =\rho \left(\frac{a x}{h}\right) \cdot \delta x
माना PQ का मध्य बिन्दु M तथा A से BC पर AD लम्ब है।तब समान्तर अक्षों के प्रमेय से
PQRS का AD के परितः जड़त्व-आघूर्ण=PQ के मध्य-बिन्दु M से गुजरने वाली समान्तर रेखा के परितः जड़त्व-आघूर्ण+पट्टिका का द्रव्यमान. AM^2=\frac{\rho ax \delta x}{h}\left\{\frac{1}{3}\left(\frac{a x}{2h}\right)^2+A M^2\right\} \\ =\frac{\rho a x \delta x}{h}\left\{\frac{1}{3}\left(\frac{a x}{2 h}\right)^2+\left(\frac{x \times AK}{h} \right)^2\right\} \\ \triangle ABC \sim \triangle APQ \\ \left[\because \frac{A M}{A K}=\frac{x}{h}\right] \\ =\frac{\rho a}{4 h^3}\left(\frac{a^2}{3}+4 A K^2\right) \int_0^h x^3 d x \\=\frac{\rho a h}{48}\left(a^2+12 A K^2\right) \\ =\left(\frac{2 M}{h a}\right) \times\left(\frac{a h}{48}\right) \times \left(a^2+12 AK^2\right) \\ =\frac{M}{24}\left(a^2+12 A K^2\right) \cdots(1) \\ A K^2=A N^2+N K^2 \\ =A N^2+(B K-B N)^2 \\ =\left(A N^2+B N^2\right)+B K^2-2 BK \cdot B N \\ =A B^2+\left(\frac{B C}{2}\right)^2-2\left(\frac{B C}{2}\right) A B \cos B
[ \because BQ \| BC तथा M,PQ का मध्य बिन्दु है]
[K,BC का मध्य बिन्दु है]
=c^2+\frac{a^2}{4}-ac \left[\left(\frac{a^2+c^2-b^2}{2 a c}\right)\right] \\ =\frac{2 b^2+2 c^2-a^2}{4} जहाँ AB=c, AC=b
(1) से AD के परितः जड़त्व-आघूर्ण
=\frac{M}{24}\left[a^2+3\left(2 b^2+2 c^2-a^2\right)\right] \\ =\left(\frac{M}{12}\right)\left(3 b^2+3 c^2-a^2\right)
Example:10.सिद्ध कीजिए कि एक दीर्घवृत्तीय पटल का किसी दो स्पर्शी रेखाओं,जो परस्पर लम्बवत हैं,के परितः जड़त्व-आघूर्णों का जोड़ सर्वदा समान रहता है।
(Prove that sum of the moments of inertia of an elliptic lamina about any two tangents at right angles to each other is always the same.)
Solution:माना स्पर्शरेखा AT,OX के साथ \theta कोण बनाती है।तब स्पर्शरेखा की समीकरण
p=ON=केन्द्र O(0,0) से स्पर्शरेखा पर लम्ब
=\frac{\left(a^2 \tan ^2 \theta+b^2\right)^{\frac{1}{2}}}{\left(1+\tan ^2 \theta\right)^{\frac{1}{2}}} \\ p=\left(a^2 \sin ^2 \theta+b^2 \cos ^2 \theta\right)^{\frac{1}{2}}
माना PQ दीर्घवृत्त का व्यास है,जो (1) के समान्तर है
I=PQ के परितः जड़त्व-आघूर्ण
=\frac{M}{4}\left(b^2 \cos ^2 \theta+a^2 \sin ^2 \theta\right) \\ \Rightarrow I=\frac{1}{4} M p^2 [(2) से]
अतः समान्तर अक्षों के प्रमेय से,स्पर्शरेखा AT के परितः जड़त्व-आघूर्ण=PQ के परितः जड़त्व-आघूर्ण+दीर्घवृत्त की संहति M को गुरुत्व केन्द्र O पर स्थापन कर स्पर्शरेखा AT के परितः जड़त्व-आघूर्ण
=\frac{4}{4} M P^2+M \times(O N)^2 \\ =\frac{1}{4} M P^2+M P^2 \\ =\frac{5}{4} M p^2
I_1=OX के साथ कोण बनानेवाली स्पर्शरेखा के परितः जड़त्व-आघूर्ण
=\frac{5}{4} M p^2=\frac{5}{4} M\left(a^2 \sin ^2 \theta+b^2 \cos ^2 \theta\right)
AT पर लम्बवत स्पर्शी \left(\frac{\pi}{2}+\theta\right) ,OX के साथ कोण बनाएगी अतः
I_2=\left(\frac{5}{4}\right) M\left[a^2 \sin ^2\left(\frac{\pi}{2}+\theta\right)+b^2 \cos ^2\left(\frac{\pi}{2}+\theta\right)\right] \\ =\left(\frac{5}{4}\right) M \left(a^2 \cos ^2 \theta+b^2 \sin^2 \theta\right)
अतः दो स्पर्शी रेखाएँ जो परस्पर लम्बवत हैं,के परितः जड़त्व-आघूर्णों का योग
I_1+I_2=\frac{5}{4} M\left(a^2 \sin ^2 \theta+b^2 \cos ^2 \theta\right) +\frac{5}{4}\left(a^2 \cos ^2 \theta+b^2 \sin ^2 \theta\right) \\ =\frac{5}{4}\left(a^2+b^2\right) \\ \Rightarrow I_1+I_2=\frac{5}{4}\left(a^2+b^2\right)
जो \theta पर निर्भर नहीं है अतः सर्वदा समान रहता है।
उपर्युक्त उदाहरणों के द्वारा गतिविज्ञान में समान्तर अक्षों का प्रमेय (Theorem of Parallel Axes in Dynamics),जड़त्व-आघूर्ण एवं गुणन के लिए समान्तर अक्षों का प्रमेय (Theorem of Parallel Axes for Moment and Product of Inertia) को समझ सकते हैं।
3.गतिविज्ञान में समान्तर अक्षों का प्रमेय की समस्याएँ (Theorem of Parallel Axes in Dynamics Problems):
(1.)a त्रिज्या तथा M संहति वाले लम्बवृत्तीय बेलन का उसके अक्ष के परितः जड़त्व-आघूर्ण ज्ञात करिये।
(Find the M. I. of a right circular cylinder of radius a and mass M about its axis.)
(2.)एक ठोस पिण्ड जिसका घनत्व \rho तथा उसका आकार कार्डिआइड r=a(1+\cos \theta) को प्रारम्भिक रेखा के परितः घुमाने से बने ठोस का है।प्रदर्शित करिए कि एक रेखा जो ध्रुव से गुजरे तथा प्रारम्भिक रेखा के लम्बवत है,के परितः जड़त्व-आघूर्ण=\frac{352}{105} \pi \rho a^5 होगा।
(A solid body of density \rho , is in the shape of the solid formed by the revolution of the cardiod r=a(1+\cos \theta) about the initial line, show that its moment of inertia about a straight line through the pole perpendicular to the initial line is \frac{352}{105} \pi \rho a^5 .)
उत्तर (Answer):(1.) \frac{1}{2} M a^2
उपर्युक्त सवालों को हल करने पर गतिविज्ञान में समान्तर अक्षों का प्रमेय (Theorem of Parallel Axes in Dynamics),जड़त्व-आघूर्ण एवं गुणन के लिए समान्तर अक्षों का प्रमेय (Theorem of Parallel Axes for Moment and Product of Inertia) को ठीक से समझ सकते हैं।
Also Read This Article:- Product of Inertia in Dynamics
4.गतिविज्ञान में समान्तर अक्षों का प्रमेय (Frequently Asked Questions Related to Theorem of Parallel Axes in Dynamics),जड़त्व-आघूर्ण एवं गुणन के लिए समान्तर अक्षों का प्रमेय (Theorem of Parallel Axes for Moment and Product of Inertia) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.जड़त्व-आघूर्ण ज्ञात करने के लिए लम्बवत अक्षों की प्रमेय का क्या कथन है? (What is the Statement of the Theorem of the Perpendicular Axis to Find the Moment of Inertia?):
उत्तर:यदि तीन परस्पर लम्बवत रेखाएँ एक-दूसरे से एक उभयनिष्ठ बिन्दु पर मिलती हों,तो एक पटल (lamina) का इसके समतल में स्थित दो रेखाओं के परितः जड़त्व-आघूर्णों का जोड़ पटल का तीसरी लम्बवत रेखा के परितः जड़त्व-आघूर्ण के बराबर होता है अर्थात सम्पूर्ण पटल का OZ के परितः जड़त्व-आघूर्ण=\Sigma m\left(x^2+y^2\right)=\Sigma m x^2+\Sigma m y^2
प्रश्न:2.जड़त्व-आघूर्ण एवं गुणन के लिए समान्तर अक्षों की प्रमेय का क्या कथन है? (What is the Statement of Parallel Axes for Moment of Inertia and Product of Inertia?)
उत्तर:किसी पिण्ड के गुरुत्व केन्द्र से होकर जानेवाली किन्हीं रेखा या रेखाओं के परितः जड़त्व-आघूर्ण व जड़त्व गुणनफल दिए हुए होने पर अन्य समान्तर रेखा या रेखाओं के परितः इन्हें ज्ञात करना
अतः पिण्ड का OX’ के परितः जड़त्व-आघूर्ण =\Sigma m\left(y^2 +z^2\right) +m\left(y^{-2}+z^{-2}\right)
प्रश्न:3.जड़त्व-आघूर्ण के लिए राउथ नियम क्या है? (What is the Routh Law for Moment of Inertia?):
उत्तर:डाॅ. राउथ (Dr. Routh) ने कुछ पिण्डों की सरल अवस्थाओं के जड़त्व-आघूर्णों को याद रखने के लिए सरल नियम का प्रतिपादन किया।
एक सममित अक्ष के सापेक्ष जड़त्व-आघूर्ण=\frac{\text{पिण्डों की संहति × लम्बवत अर्धाक्षों के वर्गों का योग}}{\text{3,4 या 5}}
पिण्ड के आयताकार या दीर्घवृत्ताकार (वृत्ताकार सहित) या दीर्घवृत्तज (गोलाकार सहित) अनुसार हर 3 या 4 या 5 होता है।
उपर्युक्त प्रश्नों के उत्तर द्वारा गतिविज्ञान में समान्तर अक्षों का प्रमेय (Theorem of Parallel Axes in Dynamics),जड़त्व-आघूर्ण एवं गुणन के लिए समान्तर अक्षों का प्रमेय (Theorem of Parallel Axes for Moment and Product of Inertia) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Theorem of Parallel Axes in Dynamics
गतिविज्ञान में समान्तर अक्षों का प्रमेय
(Theorem of Parallel Axes in Dynamics)
Theorem of Parallel Axes in Dynamics
गतिविज्ञान में समान्तर अक्षों का प्रमेय (Theorem of Parallel Axes in Dynamics) तथा लम्बवत
अक्षों का प्रमेय पर आधारित विशिष्ट सवालों को हल करके समझने का प्रयास करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.