Tangential Velocity in Dynamics
1.गति विज्ञान में स्पर्शरेखीय वेग (Tangential Velocity in Dynamics),गति विज्ञान में अभिलाम्बिक वेग (Normal Velocity in Dynamics):
गति विज्ञान में स्पर्शरेखीय वेग (Tangential Velocity in Dynamics) के साथ-साथ अभिलाम्बिक वेग,स्पर्शरेखीय तथा अभिलाम्बिक त्वरण के बारे में इस आर्टिकल में अध्ययन करेंगे।इन्हें कुछ उदाहरणों के द्वारा समझेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Radial and Transverse Acceleration
2.गति विज्ञान में स्पर्शरेखीय वेग के साधित उदाहरण (Tangential Velocity in Dynamics Solved Examples):
Example:2.एक कण एक समतलीय वक्र में गमन करता है तो कण के कोणीय वेग एवं रैखिक वेग v में सम्बन्ध लिखिए।
(A particle is moving along a plane curve then write the relation between the angular velocity and linear velocity):
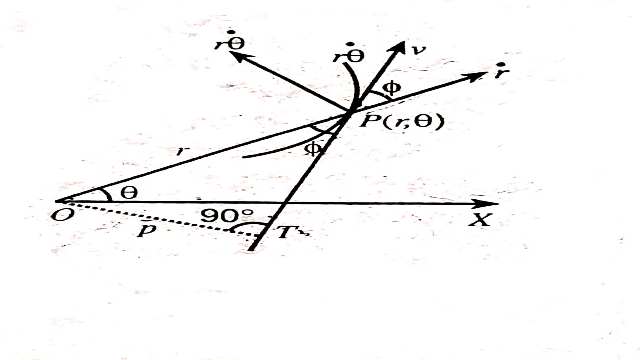
Solution:मानलो बिन्दु P पर कण का रेखीय वेग v तथा कोणीय वेग \theta है।स्पष्टतया v,वक्र के बिन्दु p पर स्पर्श रेखा के अनुदिश होगा।मानलो ध्रुवान्तर रेखा OP तथा स्पर्श रेखा PT के बीच कोण \phi है तथा ध्रुव O से स्पर्श रेखा पर खींचे गए लम्ब OT की लम्बाई p है।बिन्दु P का OP के अनुदिश वेग तथा OP के लम्बवत वेग r \dot{\theta} होता है।
अब v को OP के अनुदिश तथा इसके लम्बवत वियोजित करने पर
v \cos \phi=\dot{r} तथा v \sin \phi=r \dot{\theta} \\ \therefore \dot{\theta}=\frac{r \sin \phi}{r} \cdots(1)
पुन: त्रिभुज OTP से:
\frac{p}{r}=\sin \phi \cdots(2)
अतः (1) और (2) से:
\dot{\theta}=\frac{v p}{r^2}
जो कि रेखीय वेग तथा कोणीय वेग में अभीष्ट सम्बन्ध है।
Example:3.एक कण किसी वक्र पर इस प्रकार चलता है कि इसके स्पर्श रेखीय एवं अभिलाम्बिक त्वरण आपस में समानुपातिक है एवं उसकी स्पर्श रेखा का कोणीय वेग अचर रहता है।वक्र ज्ञात कीजिए।
(A particle moves in a curve so that its tangential and normal accelerations are proportional to each other and the angular velocity of the tangent is constant.Find the curves.)
Solution:स्पर्शरेखीय त्वरण= v \frac{d v}{d s}
अभिलाम्बिक त्वरण=\frac{v^2}{\rho} \\ \left[\because \rho=\frac{d s}{d \psi}\right]
अतः अभिलाम्बिक त्वरण=\frac{v^2}{\frac{d s}{d \psi}} \\ =v^2 \frac{d \psi}{d s} \\ v \frac{d v}{d s} \propto v^2 \frac{d \psi}{d s} \\ \Rightarrow d v=k v d \psi \\ \Rightarrow \frac{d v}{v}=k d \psi
समाकलन करने पर:
\int \frac{dv}{v}=\int k d \psi \\ \Rightarrow \log v=k \psi+B \\ \Rightarrow v=e^{k \psi+B} \\ \Rightarrow v=e^B \cdot e^{k \psi} \\ \Rightarrow \frac{d s}{d t}=e^B e^{k \psi} \cdots(1)
स्पर्श रेखा का कोणीय वेग=\frac{d \psi}{d t}=m \cdots(2)
(1) में (2) का भाग देने पर:
\Rightarrow \frac{d s}{d \psi}=\frac{e^B}{m} e^{k \psi} \\ \Rightarrow d s=2 n e^{k \psi} d \psi\left[\because \frac{e^B}{m}=n\right]
समाकलन करने पर:
\int d s=\int n e^{k \psi} d \psi \\ \Rightarrow S=\frac{n }{k}e^{k \psi}+\beta \\ \Rightarrow S=\alpha e^{k \psi} +\beta\quad\left[\because \frac{n}{k}=\alpha\right]
Example:6.यदि किसी समतल वक्र में गतिमान एक कण के स्पर्शरेखीय तथा अभिलाम्बिक त्वरण सदैव अचर रहते हो,तो सिद्ध करो कि t समय पर वक्रता त्रिज्या \rho सम्बन्ध \rho=(a t+b)^2 से प्राप्त होगा,जहाँ a व b कोई अचर है।
(If the tangential and normal acceleration of a particle describing a plane curve be constant throughout,prove that the radius of curvature at any point t is given by \rho=(a t+b)^2, where a and b are constants.)
Solution:स्पर्शरेखीय त्वरण=\frac{d v}{d t}=m
समाकलन करने पर:
\int d v=m \int d t \\ \Rightarrow v=m t+n \cdots(1)
अभिलाम्बिक त्वरण=\frac{v^2}{\rho}=k \\ \Rightarrow \rho=\frac{v^2}{k} \cdots(2)
समीकरण (1) व (2) से:
\rho=\frac{(m t+n)^2}{k} \\ \Rightarrow=\left(\frac{m}{\sqrt{k}} t+\frac{n}{\sqrt{k}}\right)^2
माना \frac{m}{\sqrt{k}}=a तथा \frac{n}{\sqrt{k}}=b \\ \Rightarrow \rho=(a t+b)^2
Example:8.एक कण समतल वक्र में इस प्रकार चलता है कि इसके स्पर्शरेखीय तथा अभिलाम्बिक त्वरण सदैव समान रहते हैं और इसका वेग e^{\tan ^{-1}\left(\frac{S}{c}\right)} के समानुपाती है जहाँ s किसी स्थिर बिन्दु से मापी गई चाप की लम्बाई है।सिद्ध करो कि पथ केटेनरी है।
(A particle moves in a plane curve in such a manner that its tangential and normal accelerations are always equal and its velocity varies as e^{\tan ^{-1}\left(\frac{S}{c}\right)},s being the length of the arc of the curve measured from the fixed point on the curve. Show that the path is a catenary.)
Solution:प्रश्नानुसार v \frac{d v}{d s}=\frac{v^2}{\rho} \\ \Rightarrow \frac{d v}{d s}=\frac{v}{\rho} \\ \Rightarrow \frac{d v}{d s}=\frac{v}{\frac{d s}{d \psi}}\left[\because \rho=\frac{d s}{d \psi}\right] \\ \Rightarrow \frac{d v}{v}=d \psi
समाकलन करने पर:
\int \frac{d v}{v}=\int d \psi \\ \log v=\psi+A \\ v=e^{\psi+A} \ldots(1) \\ v=e^B \cdot e^{\tan^{-1} \left(\frac{S}{c}\right)}(दिया है) …..(1)
(1) व (2) से:
e^B e^{\tan ^{-1}\left(\frac{S}{c}\right)}=e^{\psi+A} \\ \Rightarrow e^{\tan ^{-1}\left(\frac{S}{c}\right)}=e^{\psi+A-B}
तुलना करने पर:
\tan^{-1}\left(\frac{s}{c}\right)=\psi+A-B \\ s=c \tan (\psi+A-B)
जब \psi=0 तो s=0
अतः A-B=0
s=c \tan \psi
जो कि केटेनरी है।
Example:9.एक कण एक समतल वक्र में इस प्रकार गमन करता है कि इसका स्पर्शरेखीय त्वरण अचर रहता है और इसके स्पर्शरेखीय वेग का परिमाण तथा अभिलाम्बिक त्वरण का अनुपात अचर रहता है।सिद्ध करो कि पथ का नैज समीकरण s=A \psi^2+B \psi+C रूप में होगा।
(A point moves in a plane curve so that its tangential acceleration is constant and the magnitude of the tangential velocity and normal acceleration are in a constant ratio. Show that the intrinsic equation of the path is of the form s=A \psi^2+B \psi+C.)
Solution:स्पर्शरेखीय त्वरण v \frac{d v}{d s}=m(अचर)…..(1)
तथा \frac{v}{\frac{v^2}{\rho}}=n (अचर)
\Rightarrow v=n \frac{v^2}{\rho} \\ \Rightarrow \frac{\rho}{v}=n \ldots(2)
(1) का समाकलन करने पर:
v d v=m d s \\ \Rightarrow v^2=2 m s+k \ldots(3)
समीकरण (2) व (3) से:
\frac{\rho^2}{n^2}=2 m s+k \\ \Rightarrow \frac{\rho}{n}=\sqrt{2 m s+k} \\ \Rightarrow \frac{d s}{d \psi}=n \sqrt{2 m s+k}\left[\because \rho=\frac{d s}{d \psi}\right] \\ \Rightarrow d \psi=\frac{d s}{n \sqrt{2 m s+k}}
समाकलन करने पर:
\Rightarrow \int d \psi=\frac{1}{n} \int \frac{1}{\sqrt{2 m s+k}} d s \\ \Rightarrow n \psi+b=2 \sqrt{2 m s+k}+a \\ \Rightarrow \frac{n \psi}{2}+\frac{b-a}{2}=\sqrt{2 m s+k} \\ \Rightarrow \left(\frac{n}{2} \psi+ \frac{b-a}{2}\right)^2=2 m s+k \\ \Rightarrow \frac{n^2}{4} \psi^2+\frac{n(b-a)}{2} \psi+\left(\frac{b-a}{2}\right)^2=2 m s+k \\ \Rightarrow \frac{n^2}{4} \psi^2+\frac{n(b-a)}{2} \psi+\frac{(b-a)^2}{4}-k=2 m s \\ \Rightarrow s=\frac{n^2}{8 m} \psi^2+\frac{n(b-a)}{4 m} \psi+\frac{(b-a)^2}{8 m}-\frac{k}{2m} \\ \text { put } \frac{n^2}{8 m}=A, \frac{n(b-a)}{4 m}=B, \quad \frac{(b-a)^2}{8 m}-\frac{k}{2m}=C \\ \Rightarrow s=A \psi^2+B \psi+C
Example:10.एक कण एकसमान कोणीय वेग से किसी परवलय में उसकी नाभि के चारों ओर चलता है।सिद्ध करो किसी बिन्दु पर अभिलाम्बिक त्वरण उस बिन्दु पर पथ की वक्रता-त्रिज्या के समानुपाती होता है।
(A particle is moving in a parabola with uniform angular velocity about the focus.prove that its normal acceleration at any point is proportional to be radius of curvature of its path at the point.)
Solution:परवलय का पदिक समीकरण P^2=a r \ldots(1)
तथा \frac{d \theta}{d t}=k (अचर) (दिया है)
समीकरण (1) को r के सापेक्ष अवकलन करने पर :
2 p \frac{d p}{d r}=a \\ \Rightarrow \frac{d r}{d p}=\frac{2 p}{a} \\ \Rightarrow r \frac{d r}{d p}=\frac{r(2 p)}{a} \rho \\ \Rightarrow \rho=\frac{2 p r}{a}\left[\because r \frac{d r}{d r}=\rho \right] \\ \Rightarrow \rho=\frac{2 p}{a} \cdot \frac{p 2}{a}[(1) से ]
\Rightarrow \rho=\frac{2 p^3}{a^2} \cdots(3)
समीकरण (2) व (3) से:
\rho=\frac{2}{a^2} \cdot \frac{a^2 v}{k} \\ \Rightarrow \rho=\frac{2 v}{k} \\ \Rightarrow \rho^2=\frac{4 v^2}{k^2} \\ \Rightarrow \rho=\frac{4}{k^2} \cdot \frac{v^2}{\rho} \\ \Rightarrow \frac{v^2}{\rho} \propto \rho
अभिलाम्बिक त्वरण \propto \rho
Example:14.एक छल्ला जो एक पतली लम्बी चिकनी छड़ पर फिसल सकता है,छड़ के एक सिरे O से d दूरी पर स्थित है।छड़ को एकसमान रूप से बिन्दु O के सापेक्ष एक क्षैतिज में घुमाया जाता है।सिद्ध करो कि छल्ला वक्र r=d \cosh \theta में घूमता है।
(A ring which can slide on a thin smooth rod rests at a distance d from one end O.The rod is then set revolving uniformly about O in a horizontal plane, show that in space the ring describes the curve r=d \cosh \theta.)
Solution:छड़ को एकसमान रूप से घुमाया जाता है अतः
अरीय त्वरण \frac{d^2 r}{d t^2}-r\left(\frac{d \theta}{d t}\right)^2=0 \ldots(1)
तथा \frac{d \theta}{d t}=w \ldots(2)
(1) व (2) से:
\frac{d^2 r}{d t^2}-r \omega^2=0 \\ \Rightarrow \frac{d^2 r}{d t^2}=r \omega^2
दोनों पक्षों को 2 \frac{d r}{d t} से गुणा करने पर:
\frac{d^2 r}{d t^2} \cdot\left(2 \frac{d r}{d t}\right)=r \omega^2 \cdot 2 \frac{d r}{d t}
समाकलन करने पर:
\left(\frac{d r}{d t}\right)^2=r^2 \omega^2+A
प्रारम्भ में जब r=d ; \frac{d r}{d t}=0 \\ \therefore A =-d^2 \omega^2 \\ \left(\frac{d r}{d t}\right)^2 =r^2 \omega^2-d^2 \omega^2 \\ \frac{d r}{d t}=w \sqrt{r^2-d^2} \\ \Rightarrow \frac{d r}{\sqrt{r^2-d^2}}=\omega d t
समाकलन करने पर:
\int \frac{d r}{\sqrt{r^2-d^2}}=\int \omega d t \\ \Rightarrow \cosh ^{-1}\left(\frac{r}{d}\right) =\omega t \\ \Rightarrow r=d \cosh \omega t \ldots(3) \\ \frac{d \theta}{d t}=\omega \Rightarrow d \theta=\omega d t
समाकलन करने पर:
\int d \theta=\int \omega d t \\ \Rightarrow \theta=\omega t+B \\ \because जब t=0, \theta=0 \quad \therefore B=0 \\ \therefore \theta=\omega t \ldots(4)
(3) व (4) से:
r=d \cosh \theta
उपर्युक्त उदाहरणों के द्वारा गति विज्ञान में स्पर्शरेखीय वेग (Tangential Velocity in Dynamics),गति विज्ञान में अभिलाम्बिक वेग (Normal Velocity in Dynamics) को समझ सकते हैं।
3.गति विज्ञान में स्पर्शरेखीय वेग पर आधारित सवाल (Questions Based on Tangential Velocity in Dynamics):
(1.)एक कण एक वक्र में एकसमान वेग v (जिसके लिए s तथा \psi दोनों एकसाथ समाप्त होते हैं) से गति करता है।यदि किसी बिन्दु पर त्वरण \frac{v^2 c}{s^2+c^2} है, तो वक्र का नैज समीकरण ज्ञात करो।
(A point describes a curve (for which s and \psi vanish simultaneously) with uniform speed v.If the acceleration at any point be \frac{v^2 c}{s^2+c^2}, find the intrinsic equation of the curve.)
(2.)एक कण वक्र y=a \log \sec \left(\frac{x}{a}\right) पर इस प्रकार गमन करता है कि वक्र की स्पर्श रेखा एकसमान रूप से घूमती है;सिद्ध करो कि वक्र का परिणामी त्वरण,वक्रता-त्रिज्या के वर्ग के समानुपाती है।
(A particle moves in the curve y=a \log \sec \left(\frac{x}{a}\right) in such a way that the tangent to the curve rotates uniformly ; prove that the resultant acceleration of the particle varies as square of the radius of curvature.)
उत्तर (Answer): (1.) s=c \tan \psi
उपर्युक्त सवालों को हल करने पर गति विज्ञान में स्पर्शरेखीय वेग (Tangential Velocity in Dynamics),गति विज्ञान में अभिलाम्बिक वेग (Normal Velocity in Dynamics) को ठीक से समझ सकते हैं।
Also Read This Article:- Kepler Laws for Planetary Motion
4.गति विज्ञान में स्पर्शरेखीय वेग (Frequently Asked Questions Related to Tangential Velocity in Dynamics),गति विज्ञान में अभिलाम्बिक वेग (Normal Velocity in Dynamics) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.स्पर्शरेखीय तथा अभिलाम्बिक वेग व त्वरण के सूत्र लिखो। (Write the Formulas for Tangential and Normal Velocities and Accelerations):
उत्तर:स्पर्शरेखीय वेग=\frac{d s}{d t}=s
अभिलाम्बिक वेग=0
स्पर्शरेखीय त्वरण=\frac{d v}{d t}=\frac{d^2 s}{d t^2}=v \frac{d v}{d s}
अभिलाम्बिक त्वरण=\frac{v^2}{\rho}\left[\because \rho=\frac{d s}{d \psi}\right]
प्रश्न:2.स्पर्शरेखीय वेग तथा त्वरण की दिशा किस तरफ होगी? (In which direction will the direction of tangential velocity and tangential acceleration?):
उत्तर:स्पर्शरेखीय वेग तथा त्वरण की धनात्मक दिशा \psi के बढ़ने की दिशा में होगी।
प्रश्न:3.अभिलाम्बिक त्वरण की दिशा किस तरफ होगी? (In which the direction will the direction of normal acceleration?):
उत्तर:अभिलाम्बिक त्वरण अभिलम्ब के अनुदिश अन्दर की तरफ होगा।
उपर्युक्त प्रश्नों के उत्तर द्वारा गति विज्ञान में स्पर्शरेखीय वेग (Tangential Velocity in Dynamics),गति विज्ञान में अभिलाम्बिक वेग (Normal Velocity in Dynamics) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Tangential Velocity in Dynamics
गति विज्ञान में स्पर्शरेखीय वेग
(Tangential Velocity in Dynamics)
Tangential Velocity in Dynamics
गति विज्ञान में स्पर्शरेखीय वेग (Tangential Velocity in Dynamics) के साथ-साथ अभिलाम्बिक
वेग,स्पर्शरेखीय तथा अभिलाम्बिक त्वरण के बारे में इस आर्टिकल में अध्ययन करेंगे।इन्हें कुछ
उदाहरणों के द्वारा समझेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.