Sum of First n Terms of an AP in Maths
1.गणित में समान्तर श्रेढ़ी के प्रथम n पदों का योग (Sum of First n Terms of an AP in Maths),समान्तर श्रेढ़ी के प्रथम n पदों का योग (Sum of First n Terms of an AP Class 10):
गणित में समान्तर श्रेढ़ी के प्रथम n पदों का योग (Sum of First n Terms of an AP in Maths) ज्ञात करने के के दो सूत्र हैं।प्रथम सूत्र में यदि समान्तर श्रेढ़ी का प्रथम पद, सार्व अन्तर और पदों की संख्या ज्ञात होने पर योगफल ज्ञात किया जा सकता है जबकि द्वितीय सूत्र में पदों की संख्या, प्रथम पद और अन्तिम पद ज्ञात होने पर योगफल ज्ञात किया जा सकता है।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-General Term of Arithmetic Progression
2.गणित में समान्तर श्रेढ़ी के प्रथम n पदों का योग के साधित उदाहरण (Sum of First n Terms of an AP in Maths Solved Examples):
Example:1.उस AP के प्रथम 51 पदों का योग ज्ञात कीजिए जिसके दूसरे और तीसरे पद क्रमशः 14 और 18 है।
Solution: n=51 \\ a_n=a+(n-1) d \\ \begin{matrix} a_2=a+d=14 \ldots(1) \\ a_3=a+2 d=18 \ldots(2) \\ \quad - \quad \quad- \quad \quad- \text{ घटाने पर } \\ \hline -d=-4 \end{matrix} \\ \Rightarrow d=4
d का मान समीकरण (1) में रखने परः
a+4=14 \Rightarrow a=10 \\ S_n =\frac{n}{2}[2 a+(n-1) d] \\ S_{51} =\frac{51}{2}[2 \times 10+(51-1) 4] \\ =\frac{51}{2}[20+50 \times 4] \\ =\frac{51}{2}[20+200] \\ =\frac{51}{2} \times 220 \\ =5610
Example:2.यदि किसी AP के प्रथम 7 पदों का योग 49 है और प्रथम 17 पदों का योग 289 है तो इसके प्रथम n पदों का योग ज्ञात कीजिए।
Solution: S_n=\frac{n}{2}[2 a+(n-1) d] \\ S_7=\frac{7}{2}[2 a+(n-1) d]=49 \\ \frac{7}{2}[2 a+6 d]=49 \\ \Rightarrow \frac{7}{2} \times 2(a+3 d)=49 \\ \Rightarrow 7 a+21 d=49 \\ a+3d=7 \cdots(1) \\S_{17}= \frac{17}{2}[2 a+(17-1) d]=289 \\ \Rightarrow \frac{17}{2}[2 a+16 d]=289 \\ \Rightarrow \frac{17}{2} \times 2(a+8 d)=289 \\ \Rightarrow a+8 d=\frac{289}{17} \\ \begin{matrix} \Rightarrow a+8 d=17 \ldots(2) \\ a+3 d=-7 \ldots(1) \\ \quad - \quad \quad- \quad \quad - \text{ घटाने पर } \\ \hline 5 d=10 \end{matrix} \\ \Rightarrow d=\frac{10}{5}=2
d का मान समीकरण (1) में रखने परः
a+3 \times 2=7 \\ \Rightarrow a+6=7 \\ \Rightarrow a=7-6 \\ \Rightarrow a=1, d=2, n=n \\ S_n=\frac{n}{2} [2 a+(n-1) d] \\ =\frac{n}{2}[2 \times 1+(n-1) \times 2] \\ = \frac{n}{2}[2+2 n-2] \\ =\frac{n}{2} \times 2 n \\ \Rightarrow S_{n}=n^{2}
Example:3.दर्शाइए a_{1},a_{2}, \ldots \ldots a_{n} कि से एक AP बनती है,यदि नीचे दिए अनुसार परिभाषित हैः
(1)a_n=3+4 n (ii)a_n=9-5 n
साथ ही प्रत्येक स्थिति में प्रथम 15 पदों का योगफल ज्ञात कीजिए।
Example:3(i) a_n=3+4 n
Solution: a_n=3+4 n \\ a_1=3+4 \times 1=7 \\ a_2=3+4 \times 2=3+8=11 \\ d=a_2-a_1=11-7=4
अतः अनुक्रम 7,11,15,….AP है।
a=7,d=4, n=15 \\ S_n =\frac{n}{2}[2 a+(n-1) d] \\ S_{15} =\frac{15}{2}[2 \times 7+(15-1) \times 4] \\ =\frac{15}{2}[14+14 \times 4] \\ =\frac{15}{2}[14+56] \\ =\frac{15}{2} \times 70 \\ =15 \times 35 \\ \Rightarrow S_{15} =525
Example:3(ii) a_n=9-5 n
Solution:a_n=9-5 n \\ a_1=9-5 \times 1=9-5=4 \\ a_2=9-5 \times 2=9+0=-1 \\ d=a_2-a_1=-1-4=-5
अतः अनुक्रम 4,-1,-6,-11,….AP है।
a=4, d=-1, \quad n=15, \quad S_{n}=?\\ S_{15}=\frac{15}{2}[2 \times 4+(15-1)(-1)]\\ =\frac{15}{2}[8-14]\\ =\frac{15}{2} \times -6\\ \Rightarrow S_{15}=-45
Example:4.यदि किसी AP के प्रथम n पदों का योग 4 n-n^2 है तो इसका प्रथम पद (अर्थात् S_{1}) क्या है? प्रथम दो पदों का योग क्या है? दूसरा पद क्या है? इसी प्रकार तीसरे,10वें और nवें पद ज्ञात कीजिए।
Solution: S_n=4 n-n^2 \\ S_1=4 \times 1-1^2=4-1=3 \\ S_2=4 \times 2-2^2=4 \\ a_1=S_1=3 \\ a_2=S_2-S_1=4-3=1 \\ a_2=1 \\ d=a_2-a_1=1-3=-2 \\ a=3, d=-2, n=10 \\ a_n=a+(n-1) d \\ a_n=3+(n-1) \times-2 \\ =3-2 n+2 \\ a_n=5-2 n \\ a_{10} =5-2 \times 10 \\ \Rightarrow a_{10} =5-20 \\ \Rightarrow a_{10} =-15 \\ a_3=5-2 \times 3 \\ a_3=-1 \\ a_1=S_1=3, a_2=1,S_{2}=4,a_{3}=-1, a_{10}=-15, a_n=5-2 n
Example:5.ऐसे प्रथम 40 धन पूर्णांकों का योग ज्ञात कीजिए जो 6 से विभाज्य है।
Solution: d=6, n=40, a=6 \\ S_n =\frac{n}{2}[2 a+(n-1) d] \\ \Rightarrow S_{40}=\frac{40}{2}[2 \times 6+(40-1) \times 6] \\ =20[12+39 \times 6] \\ =20(12+234) \\ =20 \times 240 \\ \Rightarrow S_{40} =4920
Example:6.8 के प्रथम 15 गुणजों का योग ज्ञात कीजिए।
Solution: a=8, d=8, n=15 \\ S_n =\frac{n}{2}[2 a+(n-1) d] \\ S_{15} =\frac{15}{2}[2 \times 8+(15-1) \times 8] \\ =\frac{15}{2}[16+14 \times 8] \\ =\frac{15}{2}[16+112] \\ =\frac{15}{2} \times 128 \\ \Rightarrow S_{15} =960
Example:6.0 और 50 के बीच की विषम संख्याओं का योग ज्ञात कीजिए।
Solution: a=1, d=2, a_n=49 \\ a_n=a+(n-1) d \\ \Rightarrow 49=1+(n-1) \times 2 \\ \Rightarrow 49=1+2 n-2 \\ \Rightarrow 2 n=49+1 \\ \Rightarrow 2 n=50 \\ \Rightarrow n=\frac{50}{2}=25 \\ S_n=\frac{n}{2}[2 a+(n-1) d] \\ S_{25}=\frac{25}{2}[2 \times 1+(25-1) \times 2] \\ =\frac{25}{2}\left[2+24 \times 2\right] \\ =\frac{25}{2}[2+48] \\ =\frac{25}{2} \times 50 \\ \Rightarrow S_{25} =625
Example:7.निर्माण कार्य से सम्बन्धित किसी ठेके में, एक निश्चित तिथि के बाद कार्य को विलम्ब से पूरा करने के लिए,जुर्माना लगाने का प्रावधान इस प्रकार हैःपहले दिन के लिए 200 रु, दूसरे दिन के लिए 250 रु, तीसरे दिन के लिए 300 रु इत्यादि अर्थात् प्रत्येक उत्तरोत्तर दिन का जुर्माना अपने से ठीक पहले दिन के जुर्माने से 50 रु अधिक है।एक ठेकेदार को जुर्माने के रूप में कितनी राशि अदा करानी पड़ेगी, यदि वह इस कार्य में 30 दिन का विलम्ब कर देता है?
Solution: a=200, d=50, n=30\\ S_n=\frac{n}{2}[2 a+(n-1) d]\\ S_{30}=\frac{30}{2}[2 \times 200+(30-1) \times 50]\\ =\frac{30}{2}[400+29 \times 50]\\ =\frac{30}{2}[400+1450]\\ =\frac{30}{2} \times 1850\\ \Rightarrow S_{30}=27750 रु
Example:8.किसी स्कूल के विद्यार्थियों को उनके समग्र शैक्षिक प्रदर्शन के लिए 7 नकद पुरस्कार देने के लिए 700 रु की राशि रखी गई है।यदि प्रत्येक पुरस्कार अपने से ठीक पहले पुरस्कार से 20 रु कम है तो प्रत्येक पुरस्कार का मान ज्ञात कीजिए।
Solution: n=7, S_n=700, d=-20 \\ S_n=\frac{n}{2}[2 a+(n-1) d] \\ S_7=\frac{7}{2}[2 a+(7-1)(-20)] \\ \Rightarrow \frac{7}{2}[2 a+6 \times-20]=700 \\ \Rightarrow 2 a-120=700 \times \frac{2}{7} \\ \Rightarrow 2 a=200+120 \\ \Rightarrow a=\frac{320}{2} \\ \Rightarrow a=160
अतः प्रत्येक पुरस्कार का मानः
160,160-20,160-2×20,160-3×20,160-4×20,160-5×20,160-6×20
160,140,120,100,80,60,40
Example:9.एक स्कूल के विद्यार्थियों ने वायु प्रदूषण कम करने के लिए स्कूल के अन्दर और बाहर पेड़ लगाने के बारे में सोचा।यह निर्णय लिया गया कि प्रत्येक कक्षा का प्रत्येक अनुभाग अपनी कक्षा की संख्या के बराबर पेड़ लगाएगा।उदाहरणार्थ,कक्षा I का एक अनुभाग 1 पेड़ लगाएगा, कक्षा II का एक अनुभाग 2 पेड़ लगाएगा, कक्षा III का एक अनुभाग 3 पेड़ लगाएगा इत्यादि और ऐसा कक्षा XII तक के लिए चलता रहेगा।प्रत्येक कक्षा के तीन अनुभाग हैं।उस स्कूल के विद्यार्थियों द्वारा लगाए गए कुल पेड़ों की संख्या कितनी होगी?
Solution:प्रत्येक कक्षा में 3 अनुभाग हैं।
कक्षा I द्वारा लगाए गए कुल पेड़=3×1=3
कक्षा II द्वारा लगाए गए कुल पेड़=3×2=6
कक्षा III द्वारा लगाए गए कुल पेड़=3×3=9
…. ….. ……… ………. …….
…. ….. ……… ………. …….
अनुक्रम 3,6,9,….समान्तर श्रेढ़ी है।
a=3, d=3, n=12 \\ S_n =\frac{n}{2}[29+(n-1) d] \\ S_{12} =\frac{12}{2}[2 \times 3+(12-1) \times 3] \\ =\frac{12}{2}[6+11 \times 3] \\ =\frac{12}{2} \times(6+33) \\ =\frac{12}{2} \times 39 \\ \Rightarrow S_{12} =234
अतः वायु प्रदूषण को रोकने के लिए विद्यार्थियों द्वारा लगाए गए पेड़ों की संख्या 234 होगी।
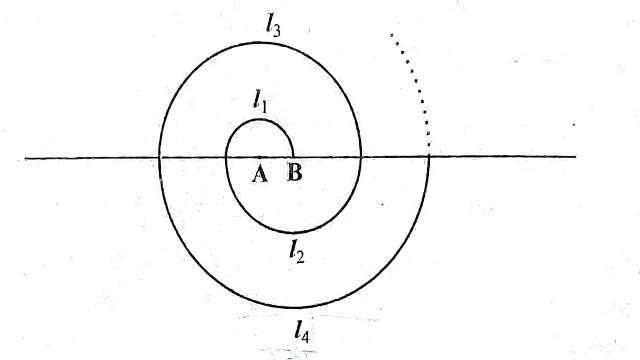
Example:10.केन्द्र A से प्रारम्भ करते हुए,बारी-बारी से केन्द्रों A और B को लेते हुए त्रिज्याओं 0.5cm,1.0cm,1.5cm, 2.0cm …….वाले उत्तरोत्तर अर्धवृत्तों को खींचकर एक सर्पिल (spiral) बनाया गया है,जैसा कि आकृति में दर्शाया गया है।तेरह क्रमागत अर्धवृत्तों से बने इस सर्पिल की कुल लम्बाई क्या है? (\pi=\frac{22}{7} लीजिए।)
Solution:पहले अर्धवृत्त की त्रिज्या r_{1}=0.5 cm
पहले अर्धवृत्त की परिधि= \pi r_{1}=\pi \times 0.5=0.5 \pi
दूसरे अर्धवृत्त की त्रिज्या=r_{2}=1.0 cm
दूसरे अर्धवृत्त की परिधि=\pi r_{2}=\pi \times 1.0=\pi
तीसरे अर्धवृत्त की त्रिज्या=r_{3}=1.5 cm
तीसरे अर्धवृत्त की परिधि=\pi r_{3}=\pi \times 1.5=1.5 \pi
अनुक्रम 0.5 \pi, \pi,1.5 \pi……है जो समान्तर श्रेढ़ी में है।
a =0.5 \pi, d=\pi-0.5 \pi=0.5 \pi, n=13 \\ S_n =\frac{n}{2}[2 a+(n-1) d] \\ S_{13} =\frac{13}{2}[2 \times 0.5 \pi+(13-1) \times 0.5 \pi] \\ =\frac{13}{2}[\pi+12 \times 0.5 \pi] \\ =\frac{13}{2}[\pi+6 \pi] \\ =\frac{13}{2} \times 7 \pi \\ =\frac{13}{2} \times 7 \times \frac{22}{7} \\ \Rightarrow S_{13} =143 सेमी
Example:11.200 लट्ठों (logs) को ढ़ेरी के रूप में इस प्रकार रखा गया हैःसबसे नीचे वाली पंक्ति में 20 लट्ठे, उससे अगली पंक्ति में 19 लट्ठे,उससे अगली पंक्ति में 18 लट्ठे इत्यादि (देखिए आकृति)।ये 200 लट्ठे कितनी पंक्तियों में रखे गए हैं तथा सबसे ऊपरी पंक्ति में कितने लट्ठे हैं?
Solution: a=20,d=19-20=-1, पंक्तियों की संख्या n=?
S_n=\frac{n}{2}[2 a+(n-1) d] \\ \Rightarrow 200=\frac{n}{2}[2 \times 20+(n-1)(-1)] \\ \Rightarrow 200 \times 2=n[40-n+1] \\ \Rightarrow 400=4 n-n^2 \\ \Rightarrow n^2-41 n+400=0 \\ \Rightarrow n^2-25 n-16 n+400=0 \\ \Rightarrow n(n-25)-16(n-25)=0 \\ \Rightarrow (n-25)(n-16)=0 \\ \Rightarrow n=16,25
अतः पंक्तियों की संख्या 16 या 25 होगी।
a_n =a+(n-1) d \\ a_{16} =20+(16-1) \times -1 \\ =20+15 \times -1 \\ =20-15 \\ a_{16} =5 \\ a_{25} =20+(25-1)(-1) \\ =20-24 \\ a_{20}=-4(जो कि असम्भव है)
अतः अन्तिम पंक्ति 16वीं में 5 लट्ठे रखे गए हैं।
Example:12.एक आलू दौड़ (Potato race) में, प्रारम्भिक स्थान पर एक बाल्टी रखी हुई है, जो पहले आलू से 5m की दूरी पर है तथा अन्य आलुओं से एक सीधी रेखा में परस्पर 3m की दूरियों पर रखा गया है।इस रेखा पर 10 आलू रखे गए हैं (देखिए आकृति)
प्रत्येक प्रतियोगी बाल्टी से चलना प्रारम्भ करती है, निकटतम आलू को उठाती है,उसे लेकर वापस आकर दौड़कर बाल्टी में डालती है,दूसरा आलू उठाने के लिए वापस दौड़ती है,उसे उठाकर वापस बाल्टी में डालती है और वह ऐसा तब तक करती है, जब तक सभी आलू बाल्टी में न आ जाएं।इसमें प्रतियोगी को कुल कितनी दूरी दौड़नी पड़ेगी?
Solution:पहला आलू उठाकर बाल्टी में डालने में तय की गई दूरी=2×5=10 मीटर
दूसरा आलू उठाकर बाल्टी में डालने में तय की गई दूरी=2×8=16 मीटर
तीसरा आलू उठाकर बाल्टी में डालने में तय की गई दूरी=2×11=22 मीटर
…. ….. ……… ………. …….
…. ….. ……… ………. …….
अनुक्रम 10,16,22,….समान्तर श्रेढ़ी में है।
S_n =\frac{n}{2}[2 a+(n-1) d] \\ S_{10} =\frac{10}{2}[2 \times 10+(10-1) \times 6] \\ =\frac{10}{2}[20+9 \times 6] \\=\frac{10}{2}[20+54] \\=\frac{10}{2} \times 74 \\ \Rightarrow S_{10} =370 मीटर
अतः प्रतियोगी द्वारा तय की गई दूरी=370 मीटर
उपर्युक्त उदाहरणों के द्वारा गणित में समान्तर श्रेढ़ी के प्रथम n पदों का योग (Sum of First n Terms of an AP in Maths),समान्तर श्रेढ़ी के प्रथम n पदों का योग (Sum of First n Terms of an AP Class 10) को समझ सकते हैं।
3.गणित में समान्तर श्रेढ़ी के प्रथम n पदों का योग पर आधारित सवाल (Questions Based on Sum of First n Terms of an AP in Maths):
(1.)एक समान्तर श्रेढ़ी के n,2n,3n पदों का योगफल क्रमशः S_{1} ,S_{2}, S_{3} है तो सिद्ध कीजिए कि S_3=3\left(S_2-S_1\right)।
(2.)यदि एक समान्तर श्रेणी के m पदों का योग ‘n’ तथा n पदों का योग ‘m’ हो तो सिद्ध कीजिए कि (m+n) पदों का योगफल – (m+n) होगा।
(3.)अनुक्रम 20,19 \frac{1}{4}, 18 \frac{1}{2}, 17 \frac{3}{4} \ldots \ldots \ldots का कौनसा पद प्रथम ऋणात्मक पद है?
उत्तर (Answer):(3.)28वाँ पद
उपर्युक्त सवालों को हल करने पर गणित में समान्तर श्रेढ़ी के प्रथम n पदों का योग (Sum of First n Terms of an AP in Maths),समान्तर श्रेढ़ी के प्रथम n पदों का योग (Sum of First n Terms of an AP Class 10) को ठीक से समझ सकते हैं।
Also Read This Article:-Sum of First n Terms of an AP Class 10
4.गणित में समान्तर श्रेढ़ी के प्रथम n पदों का योग (Sum of First n Terms of an AP in Maths),समान्तर श्रेढ़ी के प्रथम n पदों का योग (Sum of First n Terms of an AP Class 10) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.समान्तर श्रेढ़ी में n पदों के योगफल से अज्ञात पद कैसे ज्ञात करते हैं? (How to Find the Missing Term from the Sum of n Terms in the Arithmetic Progression?):
Solution:सूत्र S_n=\frac{n}{2}[2 a+(n-1) d] में चार राशियाँ S_{n},a,n और d हैं।यदि इनमें से कोई तीन ज्ञात हों तो शेष चौथी राशि को उपर्युक्त सूत्र से ज्ञात किया जा सकता है।
कभी-कभी इनमें से दो राशियाँ अज्ञात होती हैं।ऐसी स्थिति में शेष दोनों राशियाँ किसी दूसरे सम्बन्ध से ज्ञात की सकती हैं।
प्रश्न:2.समान्तर श्रेढ़ी में n पदों के योगफल से nवाँ पद कैसे ज्ञात करते हैं? (How to Find the nth Term from the Sum of n Terms in Arithmetic Progression?):
Solution:यदि किसी अनुक्रम के n पदों का योग S_{n} दिया हो तो निम्नलिखित सूत्र से अनुक्रम का nवाँ पद a_{n} ज्ञात किया जा सकता हैः a_n=S_n-S_{n-1}
प्रश्न:3.समान्तर श्रेढ़ी से nवाँ पद से अज्ञात पद कैसे ज्ञात करते हैं? (How to Find the Missing Term from the nth Term in the Arithmetic Progression?):
उत्तरःसूत्र a_n=a+(n-1)d में चार राशियाँ a,n और d हैं।यदि इनमें से कोई तीन ज्ञात हों तो शेष चौथी राशि को उपर्युक्त सूत्र से ज्ञात किया जा सकता है।
कभी-कभी इनमें से दो राशियाँ अज्ञात होती हैं।ऐसी स्थिति में शेष दोनों राशियाँ किसी दूसरे सम्बन्ध से ज्ञात की सकती हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा गणित में समान्तर श्रेढ़ी के प्रथम n पदों का योग (Sum of First n Terms of an AP in Maths),समान्तर श्रेढ़ी के प्रथम n पदों का योग (Sum of First n Terms of an AP Class 10) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Sum of First n Terms of an AP in Maths
गणित में समान्तर श्रेढ़ी के प्रथम n पदों का योग
(Sum of First n Terms of an AP in Maths)
Sum of First n Terms of an AP in Maths
गणित में समान्तर श्रेढ़ी के प्रथम n पदों का योग (Sum of First n Terms of an AP in Maths)
ज्ञात करने के के दो सूत्र हैं।प्रथम सूत्र में यदि समान्तर श्रेढ़ी का प्रथम पद, सार्व अन्तर
और पदों की संख्या ज्ञात होने
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
