Spearman Rank Difference Method

Mathematics Satyam April 21, 2023 Statistics No Comments

Contents hide

1 1.स्पियरमैन की कोटि-अन्तर रीति (Spearman Rank Difference Method),सांख्यिकी में स्पियरमैन की कोटि-अन्तर रीति (Spearman’s Rank Difference Method in Statistics):

1.1 2.स्पियरमैन की कोटि-अन्तर रीति के साधित उदाहरण (Spearman Rank Difference Method Solved Examples):

1.2 3.स्पियरमैन की कोटि-अन्तर रीति पर आधारित सवाल (Questions Based on Spearman Rank Difference Method):

1.2.1 4.स्पियरमैन की कोटि-अन्तर रीति (Frequently Asked Questions Related to Spearman Rank Difference Method),सांख्यिकी में स्पियरमैन की कोटि-अन्तर रीति (Spearman’s Rank Difference Method in Statistics) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:

1.2.2 प्रश्न:1.स्पीयरमैन की कोटि अन्तर विधि में कोटि-क्रम कैसे प्रदान करते हैं? (How Do You Assign Ranks in Spearman’s Rank Difference Method?):

1.2.3 प्रश्न:2.स्पीयरमैन की कोटि अन्तर रीति में क्रमान्तर कैसे ज्ञात किया जाता है? (How Do Spearman’s Rank Difference Method Calculate Rank Differences?):

1.2.4 प्रश्न:3.स्पीयरमैन की कोटि अन्तर रीति का सूत्र क्या है? (What is the Formula for Spearman’s Rank Differences Method?):

1.2.4.1 Spearman Rank Difference Method

2 स्पियरमैन की कोटि-अन्तर रीति (Spearman Rank Difference Method)

2.1 Spearman Rank Difference Method

1.स्पियरमैन की कोटि-अन्तर रीति (Spearman Rank Difference Method),सांख्यिकी में स्पियरमैन की कोटि-अन्तर रीति (Spearman’s Rank Difference Method in Statistics):

Spearman Rank Difference Method

स्पियरमैन की कोटि-अन्तर रीति (Spearman Rank Difference Method) को प्रोफेसर सर चार्ल्स स्पियरमैन ने व्यक्तिगत श्रेणी में सहसंबंध ज्ञात करने की इस सरल रीति का प्रतिपादन किया।इस रीति को स्पियरमैन की कोटि अंतर रीति (Spearman’s Rank Difference Method) या क्रमान्तर रीति (Ranking Method) कहते हैं।
यह रीति साधारणतः उन परिस्थितियों के लिए उपयुक्त है जहाँ तथ्यों का प्रत्यक्ष संख्यात्मक माप सम्भव न हो तथा उन्हें केवल एक निश्चित कोटि-क्रम में व्यक्त किया जा सकता हो।उदाहरणार्थ सुंदरता,बुद्धिमता,स्वास्थ्य आदि गुणात्मक तथ्यों को अंकों के रूप में मापना कठिन है,इन्हें केवल कोटि-क्रमों में व्यक्त किया जा सकता है।इन कोटि-क्रमों के आधार पर ही कोटि-अन्तर रीति द्वारा सहसंबंध गुणांक ज्ञात किया जाता है।यदि समंक श्रेणी में पद मूल्य ज्ञात न हों परन्तु उनका क्रम ज्ञात हो तो भी इस रीति द्वारा सहसंबंध गुणांक ज्ञात किया जा सकता है।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:-Coefficient of Correlation

2.स्पियरमैन की कोटि-अन्तर रीति के साधित उदाहरण (Spearman Rank Difference Method Solved Examples):

Example:35.निम्न समंकों से क्रमान्तर सहसम्बन्ध गुणांक का परिकलन कीजिएः
(Calculate the coefficient of rank correlation from the following data):

$\begin{array}{|p{1cm}|c|c|c|c|c|c|c|c|c|c|} \hline \text{X} & 48 & 33 & 40 & 9 & 16 & 16 & 65 & 24 & 16 &57 \\ \hline \text{Y} & 13 & 13 & 24 & 6 & 15 & 4 & 20 & 9 & 6 & 19 \\ \hline \end{array}$
Solution:Calculation Table of Coefficient of Correlation by Ranking Method

$\begin{tabular}{ |p{1cm}|p{2cm}|p{1cm}|p{2cm}|p{2cm}|p{2cm}|} \hline \multicolumn{2}{|c|}{\text{X-Series}} & \multicolumn{2}{|c|}{\text{Y-Series}} & Difference of Rank & Square of Rank Difference \\ \hline \text{X} & \text{Rank X} & \text{Y} & \text{Rank Y} & D & D^{2} \\ \hline 48 & 3 & 13 & 5.5 & -2.5 & 6.25 \\ \hline 33 & 5 & 13 & 5.5 & -0.5 & 0.25 \\ \hline 40 & 4 & 24 & 1 & 3 & 9 \\ \hline 9 & 10 & 6 & 8.5 & 1.5 & 2.25 \\ \hline 16 & 8 & 15 & 4 & 4 & 16 \\ \hline 16 & 8 & 4 & 10 & -2 & 4 \\ \hline 65 & 1 & 20 & 2 & -1 & 1 \\ \hline 24 & 8 & 9 & 7 & -1 & 1 \\ \hline 16 & 8 & 6 & 8.5 & -0.5 & 0.25 \\ \hline 57 & 2 & 19 & 3 & -1 & 1 \\ \hline N=10 & & & & 0 & 14 \\ \hline \end{tabular}$

$\begin{array}{|p{3cm}|c|c|c|c|c|c|c|c|c|c|} \hline \text{Towns} & A & B & C & D & E & F & G & H & I & J \\ \hline \text{Poverty} & 17 & 13 & 15 & 16 & 6 & 11 & 14 & 9 & 7 & 12\\ \hline Over crowing & 36 & 46 & 35 & 24 & 12 & 18 & 27 & 22 & 2 & 18\\ \hline \end{array}$
Solution:Calculation Table of Coefficient of Correlation by Ranking Method

$\begin{tabular}{|p{2cm}|p{1cm}|p{2cm}|p{1cm}|p{2cm}|p{2cm}|p{2cm}|} \hline & \multicolumn{2}{|c|}{\text{X-Series poverty}} & \multicolumn{2}{|c|}{\text{Y-Series over crowding}} & Difference of Rank & Square of Rank Difference \\ \hline Town & \text{X} & \text{Rank X} & \text{Y} & \text{Rank Y} & D & D^{2} \\ \hline A & 17 & 1 & 36 & 2 & -1 & 1 \\ \hline B & 13 & 5 & 46 & 1 & 4 & 16 \\ \hline C & 15 & 3 & 35 & 3 & 0 & 0 \\ \hline D & 16 & 2 & 24 & 5 & -3 & 9 \\ \hline E & 6 & 10 & 12 & 9 & 1 & 1 \\ \hline F & 11 & 7 & 18 & 7.5 & -0.5 & 0.25 \\ \hline G & 14 & 4 & 27 & 4 & 0 & 0 \\ \hline H & 9 & 8 & 22 & 6 & 2 & 4 \\ \hline I & 7 & 9 & 2 & 10 & -1 & 1 \\ \hline J & 12 & 6 & 18 & 7.5 & -1.5 & 2.25 \\ \hline TOTAL & N=10 & & & & 0 & 34.5 \\ \hline \end{tabular}$

$r(R)=1-\frac{6\left[\Sigma D^2+\frac{1}{12}\left(m^3-m\right)\right]}{N\left(N^2-1\right)} \\ =1-\frac{6\left[34.5+\frac{1}{12}\left(2^3-2\right)\right]}{10\left(10^2-1\right)} \\ =1-\frac{6\left[34.5+\frac{1}{12} \times 6\right]}{10 \times 99} \\ =1-\frac{6[34.5+0.5]}{990} \\ =1-\frac{6 \times 35}{990} \\ =1-\frac{35}{165} \\ =1-\frac{7}{33} \\ =\frac{33-7}{33} \\ =\frac{26}{33} \\ =0.7878 \\ r_{(R)} \approx+0.78$
Example:37.दस विद्यार्थियों के सांख्यिकी तथा अर्थशास्त्रों के प्राप्तांकों से क्रमान्तर सहसम्बन्ध गुणांक ज्ञात कीजिए:
(Calculate coefficient of rank correlation from the following data of marks of ten students in statistics and Economics):

$\begin{array}{|p{4cm}|c|c|c|c|c|c|c|c|c|c|} \hline Roll No. & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ \hline Marks in statistics & 45 & 56 & 39 & 54 & 45 & 40 & 56 & 60 & 30 & 36 \\ \hline Marks in Economics & 40 & 36 & 30 & 44 & 36 & 32 & 45 & 42 & 20 & 36 \\ \hline \end{array}$
Solution:Calculation Table of Coefficient of Correlation by Ranking Method

$\begin{tabular}{|p{1cm}|p{1cm}|p{2cm}|p{1cm}|p{2cm}|p{2cm}|p{2cm}|} \hline & \multicolumn{2}{|c|}{\text{X-Series Mark in statistics}} & \multicolumn{2}{|c|}{\text{Y-Marks in Economics}} & Difference of Rank & Square of Rank Difference \\ \hline Roll Number & \text{X} & \text{Rank X} & \text{Y} & \text{Rank Y} & D & D^{2} \\ \hline 1 & 45 & 5.5 & 40 & 4 & 1.5 & 2.25 \\ \hline 2 & 56 & 2.5 & 36 & 6 & -3.5 & 12.25 \\ \hline 3 & 39 & 8 & 30 & 9 & -1 & 1 \\ \hline 4 & 54 & 4 & 44 & 2 & 2 & 4 \\ \hline 5 & 45 & 5.5 & 36 & 6 & -0.5 & 0.25 \\ \hline 6 & 40 & 7 & 32 & 8 & -1 & 1 \\\hline 7 & 56 & 2.5 & 45 & 1 & 1.5 & 2.25 \\\hline 8 & 60 & 1 & 42 & 3 & -2 & 4 \\\hline 9 & 30 & 10 & 20 & 10 & 0 & 0 \\ \hline 10 & 36 & 9 & 36 & 6 & 3 & 9 \\ \hline Total & N=10 & & & & 0 & 36 \\ \hline \end{tabular}$

$r(R)=1-\frac{6\left[\Sigma D^2+\frac{1}{12}\left(m_1^3-m_1\right)+\frac{1}{12}\left(m_2^3-m_2\right)+\frac{1}{12}\left(m_3^3-m_3\right)\right]}{N\left(N^{2}-1\right )} \\ =1-\frac{6\left[36+\frac{1}{12}\left(2^3-2\right)+\frac{1}{12}\left(2^3-2\right)+\frac{1}{12}\left(3^3-3\right)\right]}{10\left(10^2-1\right)} \\ =1-\frac{6\left[36+\frac{1}{12} \times 6+\frac{1}{12} \times 6+\frac{1}{12} \times 24\right]}{10 \times 99} \\ =1-\frac{6[36+0.5+0.5+2]}{990} \\ =1-\frac{6 \times 39}{990} \\ =\frac{990-234}{990} \\ =\frac{756}{990} \\ =0.7636 \\ r_{(R)} \approx +0.764$
Example:38.दस विद्यार्थियों द्वारा लेखाशास्त्र तथा सांख्यिकी में प्राप्त अंकों का कोटि सहसम्बन्ध गुणांक +0.60 ज्ञात किया गया था।बाद में ज्ञात हुआ कि एक विद्यार्थी के दो विषयों में प्राप्तांकों का क्रमान्तर (rank difference) गलती से +3 के स्थान पर – 2 ले लिया गया था।संशोधित कोटि सहसम्बन्ध गुणांक ज्ञात कीजिए।
(The coefficient of rank correlation of marks obtained by 10 students in Accountancy and Statistics was found to be +0.60.It was later discovered that the difference in the two subjects was wrongly taken as – 2 instead of +3.Find out the correct coefficient of correlation.)
Solution: Incorrect $\quad r(R)=0.60$
Incorrect $\quad r(R)=1-\frac{6 \Sigma D^2}{N\left(N^2-1\right)} \\ \Rightarrow 0.60=1-\frac{6 \times \Sigma D^2}{10\left(10^2-1\right)} \\ =1-\frac{6 \Sigma D^2}{990} \\ =\frac{990-6 \Sigma D^2}{990} \\ \Rightarrow 6.60 \times 990=990-6 \Sigma D^2 \\ \Rightarrow 6 \Sigma D^2=990-594 \\ \Rightarrow \Sigma D^2=\frac{396}{6} \\ \Rightarrow \Sigma D^2=66$
correct $\quad \Sigma D^2 =66+9-4 \\ \Rightarrow \Sigma D^2 =71$
correct $\quad r(R)=1-\frac{6 \times \text { correct } \Sigma D^2}{N\left(N^2-1\right)} \\ =1-\frac{6 \times 71}{10\left(10^2-1\right)} \\ =1-\frac{426}{990} \\ =\frac{990-426}{990} \\ =\frac{564}{990} \\ =0.5696 \\ \Rightarrow \text {correct} \quad r(R) \approx+0.57$
Example:39.दस व्यक्तियों को प्रशिक्षण के पूर्व तथा प्रशिक्षण के पश्चात निम्नवत क्रमांकित किया गया।स्पियरमैन के सहसम्बन्ध गुणांक का परिकलन कीजिएः
(Ranking of the individuals at the start and at the finish of a training course are as follows.Calculate Spearman’s coefficient of correlation):

$\begin{array}{|p{3cm}|c|c|c|c|c|c|c|c|c|c|} \hline \text{Individual} & A & B & C & D & E & F & G & H & I & J \\ \hline Rank before & 1 & 6 & 3 & 9 & 5 & 2 & 7 & 10 & 8 & 4\\ \hline Rank after & 6 & 8 & 3 & 7 & 2 & 1 & 5 & 9 & 4 & 10\\ \hline \end{array}$
Solution:Calculation Table of Coefficient of Correlation by Ranking Method

$\begin{tabular}{|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|} \hline & Rank & Rank & Difference of Rank & Square of Rank Difference \\ \hline Individual & \text{before-X} & \text{after-Y} & D & D^{2} \\ \hline A & 1 & 6 & -5 & 25 \\ \hline B & 6 & 8 & -2 & 4 \\ \hline C & 3 & 3 & 0 & 0\\ \hline D & 9 & 7 & 2 & 4\\ \hline E & 5 & 2 & 3 & 9\\ \hline F & 2 & 1 & 1 & 1\\ \hline G & 7 & 5 & 2 & 4\\ \hline H & 10 & 9 & 1 & 1\\ \hline I & 8 & 4 & 4 & 16 \\ \hline J & 4 & 10 & -6 & 36 \\ \hline Total & N=10 & & 0 & 100 \\ \hline\end{tabular}$

$r(R)=1-\frac{6 \Sigma D^2}{N\left(N^2-1\right)} \\ =1-\frac{6 \times 100}{10\left(10^2-1\right)} \\ =1-\frac{600}{990} \\=1-\frac{20}{33} \\ =\frac{33-20}{33} \\ =\frac{13}{33}=0.3939 \\ r_{(R)} \approx +0.394$
Example:40.एक संगीत प्रतियोगिता में तीन निर्णायकों ने 10 प्रतियोगियों को निम्न स्थान प्रदान किये।सहसम्बन्ध की क्रमान्तर रीति द्वारा बतलाइए कि कौनसे दो निर्णायकों में अधिकतम समानता हैः
(In a music competition 10 competitors are ranked by three judges in the order given below.By using the Rank Correlation method discuss as to which pair of judges have the nearest approach to common taste):

$\begin{array}{|p{3cm}|c|c|c|c|c|c|c|c|c|c|} \hline \text{First Judge} & 1 & 5 & 4 & 8 & 9 & 6 & 10 & 7 & 3 & 2 \\ \hline \text{second Judge} & 4 & 8 & 7 & 6 & 5 & 9 & 10 & 3 & 2 & 1 \\ \hline \text{Third Judge} & 6 & 7 & 8 & 1 & 5 & 10 & 9 & 2 & 3 & 4 \\ \hline \end{array}$
Solution:Calculation Table of Coefficient of Correlation by Ranking Method

$\begin{tabular}{|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{1cm}|p{2cm}|p{1cm}|p{2cm}|p{1cm}|} \hline Rank & Rank & Rank & R_{1}-R_{2} & & R_{1}-R_{3} & & R_{2}-R_{3} \\ \hline \text{Judge I} & \text{Judge II} & \text{Judge III} & D_{1} & D_{1}^{2} & D_{2} & D_{2}^{2} & D_{3} & D_{3}^{2} \\ \hline 1 & 4 & 6 & -3 & 9 & -5 & 25 & -2 & 4\\ \hline 5 & 8 & 7 & -3 & 9 & -2 & 4 & 1 & 1\\ \hline 4 & 7 & 8 & -3 & 9 & -4 & 16& -1& 1\\ \hline 8 & 6 & 1 & 2 & 4 & 7 & 49 & 5 & 25\\ \hline 9 & 5 & 5 & 4 & 16 & 4 & 16 & 0 & 0 \\ \hline 6 & 9 & 10 & -3 & 9 & -4 & 16 & -1 & 1\\ \hline 10 & 10 & 9 & 0 & 0 & 1 & 1 & 1 & 1\\ \hline 7 & 3 & 2 & 4 & 16 & 5 & 25 & 1 & 1\\ \hline 3 & 2 & 3 & 1 & 1 & 0 &0 & -1 &1 \\ \hline 2 & 1 & 4 & 1 & 1 & -2 & 4 & -3 & 9\\ \hline Total & & & 0 & 74 & 0 & 156 & 0 & 44 \\ \hline \end{tabular}$

$r(R)=1-\frac{6 \Sigma D^2}{N\left(N^2-1\right)}$
I and II Judge: $r(R)=1-\frac{6 \times 74}{10\left(10^2-1\right)} \\ =1-\frac{444}{990} \\ =\frac{990-444}{990} \\ =\frac{546}{990} \\ r_{(R)}=0.55151 \\ r(R) \approx 0.5515$

I and III Judge: $r(R)=1-\frac{6 \times 156}{10\left(10^2-1\right)} \\ =1-\frac{936}{990} \\ =\frac{990-936}{990} \\ =\frac{54}{990} \\ =0.054545 \\ r(R) \approx+0.05455$

II and III Judge: $r(R)=1-\frac{6 \times 44}{10\left(10^2-1\right)} \\ =1-\frac{264}{990} \\ =\frac{990-264}{990} \\ =\frac{726}{990} \\ =0.73333 \\ r(R) \approx +0.7333$

II and III Judge have the nearest taste for music.

Spearman Rank Difference Method

Example:41.पन्द्रह विद्यार्थियों को दो विषयों में निम्नवत् क्रमांकित किया गया (कोष्ठक में दोनों विषयों में उपलब्ध क्रम एक साथ प्रस्तुत हैं), स्पियरमैन की कोटि अन्तर सूत्र द्वारा सहसम्बन्ध गुणांक ज्ञात कीजिएः
(Fifteen students were ranked in two subjects as follows (the two numbers within brackets denote the ranks obtained in two subjects),calculate coefficient of rank correlation using Spearman’s formula):
(1,10),(2,7),(3,2),(4,6),(5,4),(6,8),(7,3),(8,1),(9,11),(10,15),(11,9),(12,5),(13,14),(14,12),(15,13).)
Solution:Calculation Table of Coefficient of Correlation by Ranking Method

$\begin{tabular}{|p{2cm}|p{2cm}|p{2cm}|p{2cm}|} \hline \text{Rank-X} & \text{Rank-Y} & D & D^{2} \\ \hline 1 & 10 & -9 & 81\\ \hline 2 & 7 & -5 & 25 \\ \hline 3 & 2 & 1 & 1\\ \hline 4 & 6 & -2 & 4 \\ \hline 5 & 4 & 1 & 1 \\ \hline 6 & 8 & -2 & 4 \\ \hline 7 & 3 & 4 & 16 \\ \hline 8 & 1 & 7 & 49\\ \hline 9 & 11 & -2 & 4\\ \hline 10 & 15 & -5 & 25\\ \hline 11 & 9 & 2 & 4\\ \hline 12 & 5 & 7 & 49\\ \hline 13 & 14 & -1 & 1\\ \hline 14 & 12 & 2 & 4\\ \hline 15 & 13 & 2 & 4\\ \hline Total & N=15 & 0 & 272 \\ \hline \end{tabular}$

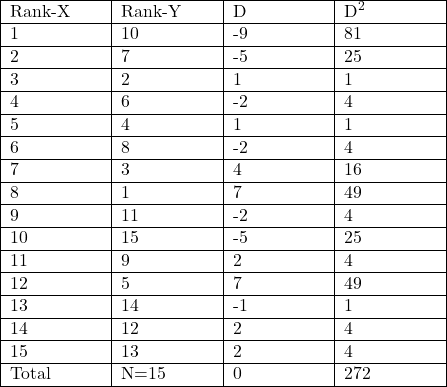
$r(R) =1-\frac{6 \Sigma D^2}{N\left(N^2-1\right)} \\ =1-\frac{6 \times 272}{15\left(15^2-1\right)} \\ =1-\frac{1632}{3360}\\=\frac{3360-1632}{3360} \\=\frac{1728}{3360}\\ =0.51422 \\ r(R) \approx 0.514$
Example:42.निम्नलिखित समंकों से स्पियरमैन का कोटि अन्तर सहसम्बन्ध का गुणांक का परिकलन कीजिएः
(From the following data calculate Spearman’s Rank coefficient of correlation):

$\begin{array}{|p{3cm}|c|c|c|c|c|c|c|c|c|c|} \hline \text{S.No.} & 1 & 5 & 4 & 8 & 9 & 6 & 10 & 7 & 3 & 2 \\ \hline \text{Rank Difference} & -2 & -4 & -1 & +3 & +2 & 0 & ? & 3 & 3 & -2 \\ \hline \end{array}$
Solution:Calculation Table of Coefficient of Correlation by Ranking Method

$\begin{tabular}{|p{2cm}|p{2cm}|p{2cm}|} \hline & Difference of Rank & Square of Rank Difference \\ \hline \text{S. No.} & D & D^{2} \\ \hline 1 & -2 & 4 \\ \hline 2 & -4 & 16 \\ \hline 3 & -1 & 1 \\ \hline 4 & +3 & 9 \\ \hline 5 & +2 & 4 \\ \hline 6 & 0 & 0 \\ \hline 7 & -2 & 4\\ \hline 8 & 3 & 9 \\ \hline 9 & 3 & 9 \\ \hline 10 & -2 & 4\\ \hline Total & 0 & 60\\ \hline\end{tabular}$

$r(R)=1-\frac{6 \Sigma D^2}{N\left(N^2-1\right)} \\ =1-\frac{6 \times 60}{10\left(10^2-1\right)} \\ =1-\frac{360}{990} \\ =\frac{990-360}{990} \\ =\frac{630}{990} \\ =\frac{7}{11} \\ =0.6363 \\ r(R) \approx+0.64$
Example:43.निम्न समंकों का क्रम प्रदान करते हुए स्पियरमैन का कोटि सहसम्बन्ध गुणांक की परिगणना कीजिएः
(Assign ranks to the following data and calculate Spearman’s rank coefficient of correlation of the data given below):

$\begin{array}{|p{1cm}|c|c|c|c|c|c|c|c|c|c|} \hline \text{X} & 5 & 10 & -6 & 4 & 0 & 8 & -3 & -7 & -2 & 9 \\ \hline \text{Y} & 3 & 8 & -1 & -5 & -3 & 7 & 1 & -4 & -2 & 8 \\ \hline \end{array}$
Solution:Calculation Table of Coefficient of Correlation by Ranking Method

$\begin{tabular}{ |p{1cm}|p{2cm}|p{1cm}|p{2cm}|p{2cm}|p{2cm}|} \hline \multicolumn{2}{|c|}{\text{X-Series}} & \multicolumn{2}{|c|}{\text{Y-Series}} & Difference of Rank & Square of Rank Difference \\ \hline \text{X} & \text{Rank X} & \text{Y} & \text{Rank Y} & D & D^{2} \\ \hline 5 & 4 & 3 & 4 & 0 & 0\\ \hline 10 & 1 & 8 & 1.5 & -0.5 & 0.25\\ \hline -6 & 9 & -1 & 6 & 3 & 9\\ \hline 4 & 5 & -5 & 10 & -5 & 25\\ \hline 0 & 6 & -3 & 8 & -2 & 4\\ \hline 8 & 3 & 7 & 3 & 0 & 0\\ \hline -3 & 8 & 1 & 5 & 3 & 9\\ \hline -7 & 10 & -4 & 9 & 1 & 1\\ \hline -2 & 7 & -2 & 7 & 0 & 0\\ \hline 9 & 2 & 8 & 1.5 & 0.5 & 0.25\\ \hline Total & N=10 & & & & 48.5\\ \hline \end{tabular}$

$r(R)=1-\frac{6 \Sigma D^2+\frac{1}{12}\left(m^3-m\right)}{N\left(N^2-1\right)} \\ =1-\frac{6 \times 48.5+\frac{1}{12}\left(2^3-2\right)}{10\left(10^2-1\right)} \\ =1-\frac{291+\frac{1}{12} \times 6}{990} \\ =1-\frac{291.5}{990} \\ =\frac{990-291.5}{990} \\ =\frac{698.5}{990} \\ =0.705555 \\ r(R) \approx+0.706$
Example:44.N युग्म अवलोकनों के लिए क्रमान्तरों के वर्गों का योग 70 है जबकि स्पीयरमैन का r=-1 है।N का मान ज्ञात कीजिएः
(The sum of the squares of differences in ranks of N observations is 70,wheras Spearman’s rank coefficient of correlation is – 1.Find out N.)
Solution: $r(R)=1-\frac{6 \Sigma D^2}{N\left(N^2-1\right)} \\ \Rightarrow-1=1-\frac{6 \times 70}{N^3-N} \\ \Rightarrow -\frac{420}{N^3-N}=-2 \\ \Rightarrow N^3-N=210 \\ \Rightarrow N^3-N=6^3-6 \\ \Rightarrow N=6$
उपर्युक्त उदाहरणों के द्वारा स्पियरमैन की कोटि-अन्तर रीति (Spearman Rank Difference Method),सांख्यिकी में स्पियरमैन की कोटि-अन्तर रीति (Spearman’s Rank Difference Method in Statistics) को समझ सकते हैं।

3.स्पियरमैन की कोटि-अन्तर रीति पर आधारित सवाल (Questions Based on Spearman Rank Difference Method):

Spearman Rank Difference Method

(1.)10 विद्यार्थियों के दो विषयों A और B में अनुपस्थितियाँ निम्नांकित हैंः
(The ranks of 10 students in two subjects A and B are as under):

$\begin{array}{|p{2cm}|c|c|c|c|c|c|c|c|c|c|} \hline \text{Students} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ \hline \text{A} & 3 & 5 & 8 & 4 & 7 & 10 & 2 & 1 & 6 & 9 \\ \hline \text{B} & 6 & 4 & 9 & 8 & 1 & 2 & 3 & 10 & 5 & 7 \\ \hline \end{array}$
कोटि सहसम्बन्ध गुणांक का परिकलन कीजिए।
(Calculate the rank correlation coefficient.)
(2.)एक अभिरुचि परीक्षण में दो निर्णायकों ने 10 प्रत्याशियों को निम्न कोटियाँ प्रदान कीः
(In an aptitude test,two judges gave the following ranks to 10 candidates):

$\begin{array}{|p{3cm}|c|c|c|c|c|c|c|c|c|c|} \hline \text{Candidate} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ \hline \text{Judge I (Rank)} & 6 & 4 & 3 & 1 & 2 & 7 & 9 & 8 & 10 & 5 \\ \hline \text{Judge II (Rank)} & 4 & 1 & 6 & 7 & 5 & 8 & 10 & 9 & 3 & 2 \\ \hline \end{array}$
क्या दोनों निर्णायकों की सहमति है?
(Is there concordance between both judges?)
उत्तर (Answers):(1.) $\rho$ =-0.257
2.) $\rho$ =+0.224, yrs
उपर्युक्त सवालों को हल करने पर स्पियरमैन की कोटि-अन्तर रीति (Spearman Rank Difference Method),सांख्यिकी में स्पियरमैन की कोटि-अन्तर रीति (Spearman’s Rank Difference Method in Statistics) को ठीक से समझ सकते हैं।

Also Read This Article:-KarlPearson Correlation Coefficient

4.स्पियरमैन की कोटि-अन्तर रीति (Frequently Asked Questions Related to Spearman Rank Difference Method),सांख्यिकी में स्पियरमैन की कोटि-अन्तर रीति (Spearman’s Rank Difference Method in Statistics) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:

प्रश्न:1.स्पीयरमैन की कोटि अन्तर विधि में कोटि-क्रम कैसे प्रदान करते हैं? (How Do You Assign Ranks in Spearman’s Rank Difference Method?):

उत्तर:X तथा Y श्रेणियों के पद मूल्य को अलग-अलग कोटि-क्रम (Ranks) प्रदान किए जाते हैं।सबसे अधिक आकार वाले मूल्य को 1,उससे कम वाले मूल्य को 2 तथा इसी प्रकार क्रम निश्चित किए जाते हैं।क्रम सबसे छोटे आकार वाले मूल्य से भी शुरू किए जा सकते हैं।ऐसी स्थिति में प्रथम क्रम छोटे मूल्य को,द्वितीय क्रम उससे बड़े आकार वाले मूल्य को तथा इस प्रकार सभी मूल्यों को क्रम दिए जायेंगे।यह ध्यान रखा जाना चाहिए कि X श्रेणी में सबसे बड़े आकार वाले मूल्य से क्रम देना शुरू किया है तो Y श्रेणी में भी सबसे बड़े आकार वाले मूल्य से ही शुरु करना होगा अर्थात् दोनों श्रेणियों में समान नीति अपनानी होगी।
यदि श्रेणी में दो या अधिक पद मूल्य समान आकार के हों तो उन्हें मिलने वाले कोटि-क्रमों का औसत ज्ञात किया जाता है यह औसत कोटि-क्रम (Average Rank or Mid-Rank) ही उन पद मूल्यों का कोटि-क्रम मान लिया जाता है।उदाहरणार्थ X श्रेणी में यदि सबसे अधिक आकार वाला मूल्य 85 हो तो उसका क्रम 1 होगा,उसके बाद यदि 75 उस श्रेणी में तीन बार आया हो तो उन्हें आगे के तीन क्रम 2,3 व 4 मिलने चाहिए थे लेकिन एक ही मूल्य को अलग-अलग कोटि-क्रम नहीं दे सकते।अतः औसत कोटि-क्रम $\frac{2+3+4}{3}$ अर्थात् 3 दिया जाएगा।इसके बाद आने वाले को 5 कोटि-क्रम दिया जाएगा।

प्रश्न:2.स्पीयरमैन की कोटि अन्तर रीति में क्रमान्तर कैसे ज्ञात किया जाता है? (How Do Spearman’s Rank Difference Method Calculate Rank Differences?):

उत्तर:(1.) क्रमान्तर या कोटि अंतर (Rank Difference) ज्ञात करने के लिए X के कोटि-क्रमों में से Y के तत्सम्बन्धी कोटि-क्रमों को घटाया जाएगा।कोटि क्रमान्तरों को संकेताक्षर ‘D’ द्वारा प्रदर्शित करते हैं।
D=कोटि-क्रम X, कोटि-क्रम Y
(2.)क्रमान्तरों (D) का बीजगणितीय जोड़ सदैव शून्य $\Sigma D=0$ होता है।
क्रमान्तर वर्ग ज्ञात करना (Calculating squares of Rank Differences):क्रमान्तरों (D) के वर्ग ज्ञात करके उन वर्गों का $\Sigma D^{2}$ जोड़ ज्ञात किया जाता है।

प्रश्न:3.स्पीयरमैन की कोटि अन्तर रीति का सूत्र क्या है? (What is the Formula for Spearman’s Rank Differences Method?):

उत्तर:सूत्र (Formula):निम्न सूत्र के माध्यम से कोटि-सहसम्बन्ध ज्ञात किया जाता हैः
सूत्र में प्रयुक्तः
$r (R)=1-\frac{6 \Sigma D^2}{N\left(N^2-1\right)}$
r(R)=कोटि अन्तर सहसम्बन्ध गुणांक (Rank Correlation Coefficient)
$\Sigma D^2$ =क्रमान्तरों के वर्गों का योग (Total of squares of rank differences)
N=पद-युग्मों की संख्या (Number of pairs of items)
टिप्पणी:कोटि-अन्तर सहसम्बन्ध के लिए संकेताक्षर $\rho$ ( $\rho$ =ग्रीक संकेताक्षर rho) का भी प्रयोग करते हैं।
समांतर क्रम के लिए संशोधन (Correlation of tied ranks):समंक श्रेणी में जब दो या दो से अधिक पद मूल्यों का आकार समान हो तो उन्हें समान क्रम प्रदान किए जाते हैं।ऐसी स्थिति में कोटि-अंतर सहसम्बन्ध निकालने के सूत्र में संशोधन करना पड़ता है।संशोधित सूत्र निम्न प्रकार हैः
$r(R)=1-\frac{6 \Sigma D^2+\frac{1}{12}\left(m^3-m\right)}{N\left(N^2-1\right)}$
सूत्र में प्रयुक्त m=उन पद मूल्यों की संख्या जिनके क्रम समान हैं।(Number of items whose ranks are equal)
यहां यह ध्यान रखना चाहिए कि उपर्युक्त सूत्र में संशोधन $\frac{1}{12}\left(m^3-m\right)$ उतनी बार करना होगा जितनी बार दोनों श्रेणियों में समान क्रम आए हैं।उदाहरणार्थ यदि X श्रेणी में 60 तीन बार, 50 दो बार तथा Y श्रेणी में 80 तीन बार आया है तो यहाँ दोनों श्रेणियों में समान क्रम तीन बार आए हैं।ऐसी परिस्थिति में सूत्र में $\frac{1}{12}\left(m^3-m\right)$ तीन बार संशोधन करना होगा तथा सूत्र का रूप निम्न प्रकार का होगाः
$r(R)=1-\frac{6\left[\Sigma D^2+\frac{1}{12}\left(m_1^3-m_1\right)+\frac{1}{12}\left(m_2^3-m_2\right)+\frac{1}{12}\left(m_3^3-m_3\right)\right]}{N\left(N^{2}-1\right )}$
उपर्युक्त प्रश्नों के उत्तर द्वारा स्पियरमैन की कोटि-अन्तर रीति (Spearman Rank Difference Method),सांख्यिकी में स्पियरमैन की कोटि-अन्तर रीति (Spearman’s Rank Difference Method in Statistics) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Instagram	click here
4.	Linkedin	click here
5.	Facebook Page	click here
6.	Twitter	click here

Spearman Rank Difference Method

स्पियरमैन की कोटि-अन्तर रीति
(Spearman Rank Difference Method)