Simple Arithmetic Mean and Quartile
1.सरल समान्तर माध्य और चतुर्थक (Simple Arithmetic Mean and Quartile),सांख्यिकी में बहुलक और मध्यका (Mode and Median in Statistics):
सरल समान्तर माध्य और चतुर्थक (Simple Arithmetic Mean and Quartile) के इस आर्टिकल में समान्तर माध्य,बहुलक,मध्यका और चतुर्थकों पर आधारित सवालों को हल करके समझने का प्रयास करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Arithmetic Mean and Mode in Statistics
2.सरल समान्तर माध्य और चतुर्थक के साधित उदाहरण (Simple Arithmetic Mean and Quartile Solved Examples):
Example:66.माना एक कक्षा में 100 छात्र हैं।उनके प्राप्तकों को समान अन्तर के 7 वर्गों वाले आवृत्ति वितरण में सारणीयन किया गया है।पहला वर्ग ’10-20′ है।4थे,5वें तथा 6ठे वर्ग की ओर ‘से कम’ संचयी आवृत्तियां क्रमशः 45,75 तथा 95 है।मध्यका अंक ज्ञात कीजिए।बहुलक तथा माध्य भी ज्ञात कीजिए।यदि दूसरे वर्ग की आवृत्ति पहले वर्ग की आवृत्ति की दुगुनी है,परन्तु तीसरे वर्ग की आवृत्ति के बराबर है तथा चौथे वर्ग की आवृत्ति पांचवें वर्ग की आवृत्ति से आधी है।
(There are 100 students in a class.Their marks have been tabulated in a frequency distribution having seven class-intervals is 10-20.The cumulative frequencies of the 4th,5th and 6th class-intervals are 45,75 and 95 respectively.Calculate the median marks.Also find the mode and the mean if the frequency of the second class is double of the first class but equal to the third class and the frequency of the fourth class is half of the fifth class.)
Solution:Let the frequency of the first class (10-29) is=x
frequency of third and fourth class=2x,2x
frequency of six class 95-75=20
frequency of fifth class 75-45=30
frequency of fourth class=\frac{1}{2} \times 30=15
frequency of seventh class=5
x+2 x+2 x+15+30+20+5=100 \\ \Rightarrow 5 x+70=100 \\ \Rightarrow x=\frac{100-70}{5} \\ \Rightarrow x=\frac{30}{5}=6 \\ x=6,2 x=2 \times 6=12
Calculation Table of Mean, Median and Mode
समान्तर माध्य (\overline{X})=A+\frac{\Sigma f d x^{\prime}}{\Sigma f} \times i \\ =45+\frac{31}{100} \times 10 \\ =45+3.1 \\ \Rightarrow \overline{X}=48.1
मध्यका m=\frac{N}{2}=\frac{100}{2}=50
It falls in 75 cf so median group 50-60
l_1=50, i=60-50=10, f=30, c=45
मध्यका (M)=l_1+\frac{i}{f}(m-c) \\ =50+\frac{10}{30}(50-45) \\ =50+\frac{1}{3} \times 5 \\ =50+1.666 \\ \Rightarrow M \approx 51.67
बहुलक
निरीक्षण द्वारा
सबसे अधिक बारम्बारता 50-60 समूह की है अतः यह बहुलक वर्ग है।
l_1=50, \quad i=60-50=10 \\ f_0=15, f_1=30, f_2=20 \\ \Delta_1=f_1-f_0=30-15=15 \\ \Delta_2=f_1-f_2=30-20=10
बहुलक (Z)=l_1+\frac{\Delta_1}{\Delta_1+\Delta_2} \times i \\ =50+\frac{15}{15+10} \times 10 \\ =50+\frac{15}{25} \times 10 \\ =50+6 \\ \Rightarrow z=56
समूहीकरण द्वारा

उपर्युक्त विश्लेषण से स्पष्ट है कि 50-60 वर्ग 6 बार (सबसे अधिक बार) आवृत्त होता है जो बहुलक वर्ग है।अतः निरीक्षण तथा समूहीकरण द्वारा बहुलक वर्ग समान है फलतः
बहुलक (Z)=56
Example:67.निम्नलिखित आवृत्ति बंटन से समान्तर माध्य,मध्यका तथा चतुर्थकों का परिकलन कीजिए:
(Calculate the Arithmetic Mean,Median and Quartiles of the following frequency distribution):
Solution:Calculation Table of Arithmetic,Median and Quartiles
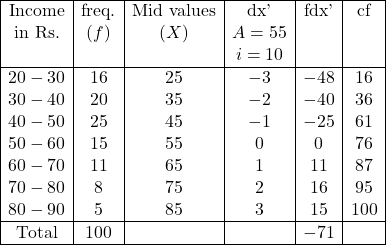
समान्तर माध्य (\overline{X})=A+\frac{\Sigma f d x^{\prime}}{N} \times i \\ =55-\frac{71}{100} \times 10 \\ =55-7.1 \\ \Rightarrow \overline{X} =47.9
मध्यका m=\frac{N}{2}=\frac{100}{2}=50
It lies in 61 cf so median group is 40-50
l_1=40, i=50-40=10, f=25, c=36
मध्यका (M)=l_1+\frac{i}{f}(m-c) \\ =40+\frac{10}{25}(50-36) \\ =40+\frac{2}{5} \times 14 \\ =40+\frac{28}{5} \\ =40+5.6 \\ \Rightarrow M=45.6
प्रथम चतुर्थक (Q_{1}) \\ q_1=\frac{N}{4}=\frac{100}{4}=25
25 lies in 36 cf so Quartile 1st group 30-40
l_1=30, i=40-30=10, f=20, c=16 \\ Q_1=l_1+\frac{i}{f}\left(q_1-c\right) \\ =30+\frac{10}{20}(25-16) \\ =30+\frac{1}{2} \times 9 \\ \Rightarrow Q_1=30+4.5
तृतीय चतुर्थक Q_{3} \\ q_3=\frac{3 N}{4}=\frac{3 \times 100}{4}=75
It falls in 50-60 group
l_1=50, i=60-50=10 ; f=15, c=61 \\ Q_3=l_1+\frac{i}{f}\left(q_3-c\right) \\ =50+\frac{10}{15}(75-61) \\ =50+\frac{2}{3} \times 14 \\ =50+\frac{28}{3} \\ =50+9.333 \\ =59.333 \\ \Rightarrow Q_3 \approx 59.33
Example:68.निम्नलिखित सूचना एक कारखाने के श्रमिकों की मजदूरी,उनके कुल कार्य-घण्टे तथा प्रति श्रमिक औसत कार्य घण्टों से सम्बन्धित है।प्रति श्रमिक औसत मजदूरी तथा बहुलक मजदूरी ज्ञात कीजिए।यह भी बतालाइए कि मध्य के 50% श्रमिकों की मजदूरी का विस्तार क्या है:
(The following information relate to the wage of workers of a factory,their total working hours and the average working hours per worker.Calculate the average wages per worker and the modal wages.Also find out the range of wage of middle 50% of the workers.)

Solution: \text { No of workers}=\frac{\text{Total hrs worked}}{\text{Average hrs per worker}} \\ =\frac{108}{9}=12, \frac{120}{8}=15, \frac{170}{85}=20 \\ \frac{195}{7.5}=26, \frac{119}{7}=17 ; \frac{60}{6}=10
Calculation Table of Mean,Mode and Quartiles

समान्तर माध्य (\overline{X})=A+\frac{\Sigma f d x^{\prime}}{N} \times i \\ =130+\frac{51}{100} \times 20 \\ =130+10.20 \\ \Rightarrow \overline{X}=140.20
बहुलक
निरीक्षण द्वारा
सबसे अधिक बारम्बारता 26 है अतः बहुलक वर्ग 140-160 है।
l_1=140, i=160-140=20 \\ f_0=20, f_1=26, f_2=17 \\ \Delta_1=f_1-f_0=26-20=6 \\ \Delta_2=f_1-f_2=26-17=9
बहुलक (Z)=l_1+\frac{\Delta_1}{\Delta_1+\Delta_2} \times i \\ =140+\frac{6}{6+9} \times 20 \\ =140+\frac{6}{15} \times 20 \\ \Rightarrow z=140+8=148
समूहीकरण

उपर्युक्त विश्लेषण से स्पष्ट है कि 140-160 वर्ग 6 बार (सबसे अधिक बार) आवृत्त होता है जो बहुलक वर्ग है।अतः निरीक्षण तथा समूहीकरण द्वारा बहुलक वर्ग समान है फलतः
बहुलक (Z)=148
प्रथम चतुर्थक (Q_{1}) \\ q_1=\frac{N}{4}=\frac{100}{4}=25
It falls in 100-120 group
l_1=100, i=120-100=20, f=15, c=12 \\ Q_1=\ell_1+\frac{i}{f}\left(q_1-c\right) \\ =100+\frac{20}{15}(25-12) \\ =100+\frac{4}{3} \times 13 \\ =100+17.333 \\ \Rightarrow Q_1 \approx 117.33
तृतीय चतुर्थक (Q_3) \\ q_3=\frac{3 N}{4}=\frac{3 \times 100}{4}=75
It falls in 160-180 group
l_1=160, i=180-160=20, f=17, c=73 \\ Q_3=l_1+\frac{i}{f}\left(q_3-c\right) \\ =160+\frac{20}{17}(75-73) \\ =160+\frac{20}{17} \times 2 \\ =160+\frac{40}{17} \\ =160+2.352 \\ \Rightarrow Q_3 \approx 162.35
Range of wage of middle 50%=Q_3-Q_1
=162.35-117.33=45.02
Example:69.निम्नलिखित समंक एक संस्था के कर्मचारियों के दो वर्षों की आय से सम्बन्धित है:
(The following data relate to income of employees of a concern in two different years):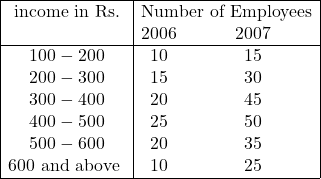
2006 के अन्तिम वर्ग में 10 कर्मचारियों की आय 8,000 रु. तथा 2007 में अन्तिम में 25 कर्मचारियों की आय 20,000 रु. थी (i)2006 तथा 2007 वर्षों के लिए सभी कर्मचारियों की कुल आय ज्ञात कीजिए; (ii)2006 के लिए आय का वह विस्तार ज्ञात कीजिए जिसमें मध्य 50% कर्मचारी आते हों।
(The total income of 10 employees in the last group in 2006 was Rs. 8,000,whereas of 25 employees in 2007 was Rs. 20,000 (i)find out the total income of all employees in the years 2006 and 2007;(ii)ascertain the range of income of middle 50% employees in the year 2006.)
Solution:Calculation Table of Total Income

(i)Total income (2006)=42500
Total income (2007)=87250
(ii)प्रथम चतुर्थक (Quartile 1st)
q_1=\frac{N}{2}=\frac{100}{4}=25
It falls in 200-300 group
l_1=200, i=300-200=100,f=15, c=10 \\ Q_1=l_1+\frac{i}{f}\left(q_1-c\right) \\ =200+\frac{100}{15}(25-10) \\ =200+\frac{20}{3} \times 15 \\ =200+100 \\ \Rightarrow Q_1=300 \\ q_3=\frac{3 N}{4}=\frac{3 \times 100}{4}=75
It falls in 500-600 group
l_1=500, i=600-500=100, f=20, c=70 \\ Q_3 =l_1+\frac{i}{f}\left(q_3-c\right) \\ =500+\frac{100}{20}(75-70) \\ \Rightarrow Q_3 =500+5 \times 5=525
Range of income of middle 50%=Q_3-Q_{1}
=525-300=225
Example:70.निम्नलिखित सारणी में प्रस्तुत समंकों से मध्यका,अपर चतुर्थक तथा उन श्रमिकों की संख्या ज्ञात कीजिए जिन्हें 47 रु. से 55 रु. प्रति सप्ताह प्राप्त होते हैं:
(From the data given in the following table, calculate median,upper quartile and the number of wage earners receiving between Rs. 47 and 55 per week):

Solution:Calculation Table of Median,Upper Quartile and Range
मध्यका: m=\frac{N}{2}=\frac{249}{2}=124.5
It lies in 177 cf so median group 50-52
l_1=50, i=52-50=2,f=62, c=115 \\ M=l_1+\frac{i}{f}(m-c) \\ =50+\frac{2}{62}(124.5-115) \\ =50+\frac{1}{31} \times 9.5 \\ =50+0.306 \\ M \approx 50.31
तृतीयक चतुर्थक (Quartile 3rd)
q_3=\frac{3 N}{4}=\frac{3 \times 249}{4}=186.75
It falls in 52-54 group
l_1=52, i=54-52=2, f=39, c=177 \\ Q_3=\ell_1+\frac{i}{f}\left(q_3-c\right) \\ =52+\frac{2}{39}(186.75-177) \\ =52+\frac{2}{39} \times 9.75 \\ =52+\frac{19-5}{39} \\ =52+0.5 \\ \Rightarrow Q_3=52.5
ऐसे श्रमिकों की संख्या जिनकी साप्ताहिक मजदूरी (47-55) रु. के मध्य है।
47 रु. से कम प्राप्त करने वाले श्रमिकों की संख्या:
47 रु. की मजदूरी वर्ग 46-48 है।
l_1=46, i=48-46=2, c=26,f=30 \\ l_1+\frac{i}{f}\left(p_x-c\right)=47 \\ \Rightarrow 46+\frac{2}{30}(p_{x}-36)=47 \\ \Rightarrow \frac{1}{15}(p_{x}-36)=47-46 \\ \Rightarrow p_{x}-36=1 \times 15 \\ \Rightarrow p_{x}=36+15=51
इसी प्रकार 55 रु. की मजदूरी वर्ग 54-56 है।
l_1=54, c=56-54=2, c=216, f=20 \\ l_{1}+\frac{i}{f}(p_{x}-c)=55 \\ \Rightarrow 54+\frac{2}{20}\left(p_x-216\right)=55 \\ \Rightarrow \frac{1}{10}\left(p_x-216\right)=55-54 \\ \Rightarrow p_x-216=1 \times 10 \\ \Rightarrow p_x=216+10 \\ \Rightarrow p_x=226
No. of wage earners receiving between Rs. 47 to 55 per week=226-51=175
Example:71.लघु उद्योगों की 500 इकाइयों में विनियोग पर प्रत्याय 0 से 30% तक विस्तारित थी तथा किसी भी इकाई में हानि नहीं थी।5% इकाइयों की प्रत्याय 0 से 5% तक (5 को सम्मिलित करते हुए) थी जबकि 15% इकाइयों द्वारा 5% से अधिक लेकिन 10% तक प्रत्याय अर्जित की गई।मध्यका प्रत्याय 15% तथा प्रत्याय का ऊपरी चतुर्थक (upper Quartile) 20% था।सबसे अधिक प्रत्याय (25% से अधिक) 50 इकाइयों द्वारा अर्जित की गई।इस सूचना को आवृत्ति वितरण के रूप में 5% वाले वर्गान्तरों में प्रस्तुत कीजिए तथा प्रत्याय की ऐसी दर का परिकलन कीजिए जिसके आसपास अधिकतम इकाइयों का घनत्व हो।
(In 500 small-scale industrial units the return on investments ranged from 0 to 30% and no unit sustained any loss.5% of the units had returns ranging from 0 to 5% (including 5) and 15% of the units earned returns exceeding 5% but not exceeding 10%.The median rate of return was 15% and the upper quartile 20%.The upper most layer of returns exceeding 25% was earned by 50 units.Present this information in the form of a frequency table with intervals of 5% each and calculate the rate of return around which there is maximum concentration on the units.)
Solution:0-5% unit=500 \times \frac{5}{100}=25
5-10% unit=500 \times \frac{15}{100}=75
Let 15-20 unit =x, 20-25 \rightarrow y and then 10-25 \rightarrow 350-x-y,25-30 \rightarrow 50
Calculation Table

मध्यका (M)=15
m=\frac{N}{2}=\frac{520}{2}=250
It lies in 450-x-y cf and median group is 15-20
l_1=15, i=20-15=5 , c=450-x-y, f=x
मध्यका (M)=l_1+\frac{i}{f}(m-c) \\ \Rightarrow 15+\frac{5}{x}(250-450+x+y)=15 \\ \Rightarrow \frac{5}{x}(-200+x+y)=0 \\ \Rightarrow x+y=200 \cdots(1)
ऊपरी चतुर्थक 20% अतः यह 20-25% वर्ग में है।
q_3=\frac{3N}{4}=\frac{3 \times 500}{4}=375 \\ l_1=20, \quad i=25-20=5, f=y, c=450-y \\ q_3=l_1+\frac{i}{5}\left(q_3-c\right) \\ \Rightarrow 20+\frac{5}{y}(375-450+y)=20 \\ \Rightarrow \frac{5}{y}(-75+y)=0 \\ \Rightarrow y=75 तथा x+75=200 \\ \Rightarrow x=125 [(1) से]
10-15 group की आवृत्ति=350-x-y
=350-125-75=150
अतः आवृत्तियां होंगी:25,75,150,125,75,50
बहुलक:निरीक्षण द्वारा
सबसे अधिक बारम्बारता 150 है अतः बहुलक वर्ग 10-15% है।
l_1=10, \quad i=15-10=5, \\ f_0=75, f_1=150, f_2=125 \\ \Delta_1=f_1-f_0=150-75=75 \\ \Delta_2=f_1-f_2=150-125=25
बहुलक (Z)=l_1+\frac{\Delta_1}{\Delta_1+\Delta 2} \times i \\ =10+\frac{75}{75+25} \times 5 \\ =10+\frac{75}{100} \times 5 \\ =10+3.75 \\ \Rightarrow z=13.25 \%
3.सरल समान्तर माध्य और चतुर्थक पर आधारित सवाल (Questions Based on Simple Arithmetic Mean and Quartile):
(1.)500 मजदूरों के समूह में 4% की मासिक मजदूरी 60 रु. से कम थी और 15% मजदूरों की मजदूरी 62.50 रु. से कम थी।15% मजदूरों ने 95 रु. और इससे अधिक मजदूरी कमाई और उनमें से 5% को 100 रु. और अधिक प्राप्त हुए।मध्यका और चतुर्थक मजदूरियाँ क्रमशः 82.75,72.75 और 90.50 रु. थी।चतुर्थ (4th) और षष्ठम (6th) दशमक मजदूरी क्रमशः 78.75 रु. और 85.34 रु. थी।55 से 105 रु. तक का सम्पूर्ण विस्तार मानते हुए इस सूचना को एक आवृत्ति बंटन के रूप में प्रस्तुत कीजिए।
(In a group of 500 wage-earners,the monthly wages of 40% were under Rs. 60 and those of 15% were under Rs. 62.50,15% of the workers earned Rs. 95 and over and 5% of them got Rs. 100 and over.The median and quartile wages were Rs. 82.25,72,75 and 90.50 respectively.The fourth and sixth decile wages were Rs. 78.75 and 85.34 respectively.Assume a range of Rs. 55 to 105 and put this information in the form of a frequency distribution.)
(2.)निम्न मजदूरी-वितरण (wage-distribution) का मध्यका (median) और भूयिष्ठक (mode) क्रमशः 33.5 रुपये और 34 रुपये हैं किन्तु सारणी में से तीन आवृत्तियां अज्ञात (missing) है।अज्ञात आवृत्तियों को ज्ञात कीजिए।
\begin{array}{|c|c|} \hline \text{मजदूरी } & \text{ (मजदूरों की संख्या) }\\ \text{(रु. में)} & \text{(आवृत्ति) } \\ \hline 0-10 & 4 \\ 10-20 & 16 \\ 20-30 & ? \\ 30-40 & ? \\ 40-50 & ? \\ 50-60 & 6 \\ 60-70 & 4 \\ \hline total & 230\\ \hline \end{array}
उत्तर (Answers):(1.)Table
\begin{array}{|c|c|} \hline \text{मजदूरी } & \text{ (मजदूरों की संख्या) }\\ \text{(रु.)} & \text{(आवृत्ति) } \\ \hline 55-60 & 20 \\ 60-62.5 & 55 \\ 62.5-72.75 & 50 \\ 72.75-78.75 & 75 \\ 78.75-82.25 & 50 \\ 82.25-85.34 & 50 \\ 85.34-90.50 & 75 \\ 90.50-95 & 50 \\ 95-100 & 50 \\ 100-105 & 25 \\ \hline \end{array}
(2.)60,100,40
उपर्युक्त प्रश्नों के उत्तर द्वारा सरल समान्तर माध्य और चतुर्थक (Simple Arithmetic Mean and Quartile),सांख्यिकी में बहुलक और मध्यका (Mode and Median in Statistics) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
Also Read This Article:-Median and Average in Statistics
4.सरल समान्तर माध्य और चतुर्थक (Frequently Asked Questions Related to Simple Arithmetic Mean and Quartile),सांख्यिकी में बहुलक और मध्यका (Mode and Median in Statistics) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.चतुर्थक से क्या तात्पर्य है? (What is Meant by Quartile?):
उत्तर:यह एक अत्यधिक महत्त्वपूर्ण माप है जो सबसे अधिक प्रयोग में आता है।जब किसी अनुविन्यसित श्रेणी को चार समान भागों में बाँटा जाना हो तो उसमें तीन चतुर्थक होंगे।प्रथम चतुर्थक को निचला चतुर्थक (Lower Quartile),दूसरे को मध्यका तथा तृतीय चतुर्थक को उच्च चतुर्थक (Upper Quartile) कहते हैं।
प्रश्न:2.पंचमक से क्या तात्पर्य है? (What is Meant by Quantiles?):
उत्तर:श्रेणी को पाँच बराबर भागों में बाँटने पर चार पंचमक होंगे जिन्हें क्रमशःQ_{n1}, Q_{n2}, Q_{n3}, Q_{n4} द्वारा व्यक्त किया जाता है।
प्रश्न:3.अष्टमक से क्या तात्पर्य है? (What is Meant by Octiles?):
उत्तर:श्रेणी को आठ बराबर भागों में बाँटने पर सात अष्टमक होंगे जिन्हें O_{1},O_{2},O_{3}, \cdots O_{7} आदि द्वारा व्यक्त किया जाता है।
उपर्युक्त प्रश्नों के उत्तर द्वारा सरल समान्तर माध्य और चतुर्थक (Simple Arithmetic Mean and Quartile),सांख्यिकी में बहुलक और मध्यका (Mode and Median in Statistics) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Simple Arithmetic Mean and Quartile
सरल समान्तर माध्य और चतुर्थक
(Simple Arithmetic Mean and Quartile)
Simple Arithmetic Mean and Quartile
सरल समान्तर माध्य और चतुर्थक (Simple Arithmetic Mean and Quartile) के इस आर्टिकल में
समान्तर माध्य,बहुलक,मध्यका और चतुर्थकों पर आधारित सवालों को हल करके समझने का प्रयास करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.








