Similarity of Triangles Class 10
1.त्रिभुजों की समरूपता कक्षा 10 (Similarity of Triangles Class 10),त्रिभुजों की समरूपता के लिए कसौटियाँ कक्षा 10 (Criteria for Similarity of Triangles Class 10):
त्रिभुजों की समरूपता कक्षा 10 (Similarity of Triangles Class 10) में दो त्रिभुज समरूप होते हैं यदि उनकी संगत भुजाएँ एक ही अनुपात में हों या उनके संगत कोण बराबर हों अथवा दो भुजाएँ एक ही अनुपात में तथा उनके बीच का कोण बराबर हो।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Criteria for Similarity of Triangles
2.त्रिभुजों की समरूपता कक्षा 10 के साधित उदाहरण (Similarity of Triangles Class 10 Solved Examples):
Example:10.CD और GH क्रमशः \angle ACB और \angle EGF के ऐसे समद्विभाजक हैं कि बिन्दु D और H क्रमशः \triangle ABC और \triangle FEG की भुजाओं AB और FE पर स्थित हैं।यदि \triangle ABC \sim \triangle FEG है तो दर्शाइए किः
(i)\frac{CD}{GH}=\frac{AC}{FG}
(ii)\triangle DCB \sim \triangle HGE
(iii)\triangle DCA \sim \triangle HGF
Solution:दिया है (Given): \triangle ABC तथा \triangle FEG में CD और GH क्रमशः \angle ACB और \angle EGF के समद्विभाजक हैं अर्थात् \angle 1=\angle 2 \text { और } \angle 3=\angle 4 तथा \triangle ABC \sim \triangle FEG
सिद्ध करना है (To Prove):(i)\frac{CD}{GH}=\frac{AC}{FG}
(ii)\triangle DCB \sim \triangle HGE
(iii)\triangle DCA \sim \triangle HGF
उपपत्ति (To Proof):(i) \triangle ABC \sim \triangle FEG (दिया है)
तथा \therefore \angle A=\angle F, \angle B=\angle E \text { तथा } \angle C=\angle G \cdots(1) \\ \Rightarrow \frac{1}{2} \angle C=\frac{1}{2} \angle G \\ \angle 1=\angle 2=\angle 3=\angle 4 \cdots(2)\\ \triangle ACD \text { तथा } \triangle FGH में
\angle A=\angle F [(1) से]
\angle 2=\angle 3 [(2) से]
AA समरूपता गुणधर्म से
\triangle ACD \sim \triangle FGH \\ \Rightarrow \frac{C D}{G H}=\frac{AC}{FG}
(समरूप त्रिभुजों की संगत भुजाएँ समानुपाती होती है)
(ii) \triangle DCB तथा \triangle HGE में
\angle B=\angle E[(1) से]
\angle 1=\angle 4 [(2) से]
AA समरूपता गुणधर्म से
\triangle DCB \sim \triangle HGE
(iii) \triangle DCA \text { तथा } \triangle HGF में
\angle A=\angle F [(1) से]
\angle 2=\angle 3 [(2) से]
AA समरूपता गुणधर्म से
\triangle DCA \sim \triangle HGF
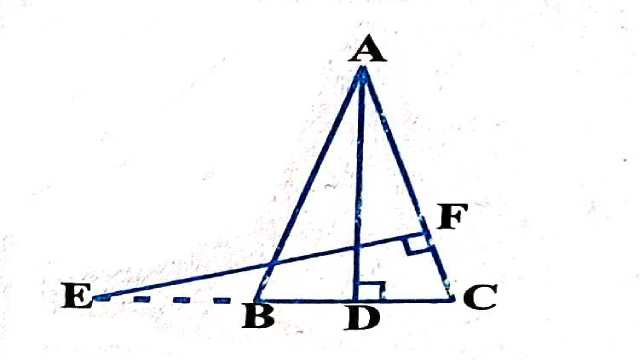
Example:11.आकृति में AB=AC वाले एक समद्विबाहु त्रिभुज ABC की बढ़ाई गई भुजा CB पर स्थित E एक बिन्दु है।यदि EF \perp AC और AD \perp BC है तो सिद्ध कीजिए कि \triangle ABD \sim \triangle ECF है।
Solution:दिया है (Given):समद्विबाहु \triangle ABC में AB=AC है तथा CB को E तक इस प्रकार बढ़ाया गया है कि EF \perp AC और AD \perp BC है।
सिद्ध करना है (To Prove): \triangle ABD \sim \triangle ECF
उपपत्ति (Proof): \triangle ABC में
AB=AC (दिया है)
\therefore \angle B =\angle C (त्रिभुज में समान भुजाओं के सम्मुख कोण बराबर होते हैं)
\triangle ABD तथा \triangle ECF में
\angle ABD=\angle ECF [(1) से]
\angle ADB=\angle EFC=90^{\circ} (दिया है)
AA समरूपता गुणधर्म से
\triangle ABD \sim \triangle ECF
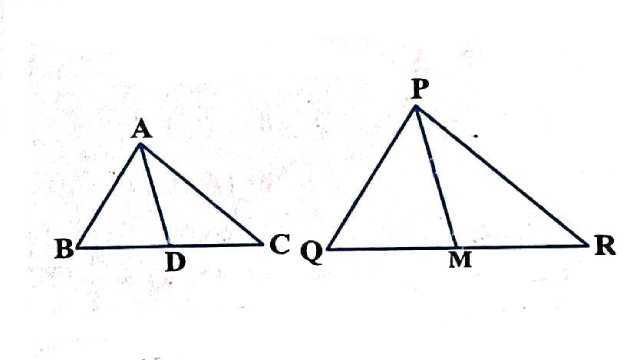
Example:12.एक त्रिभुज ABC की भुजाएँ AB और BC तथा माध्यिका AD एक अन्य त्रिभुज PQR की क्रमशः भुजाओं PQ तथा QR तथा माध्यिका PM के समानुपाती है (देखिए आकृति)।दर्शाइए कि \triangle ABC \sim \triangle PQR है।
Solution:दिया है (Given): \triangle ABC तथा \triangle PQR में
\frac{AB}{PQ}=\frac{BC}{QR}=\frac{AD}{DM} तथा BC=2BD व QR=2QM
सिद्ध करना है (To Prove): \triangle ABC \sim \triangle PQR
उपपत्ति (Proof): \frac{B C}{Q R}=\frac{A D}{P M} (दिया है)
\Rightarrow \frac{2 B D}{2 Q M}=\frac{A D}{A M} (AD व PM माध्यिका है)
\Rightarrow \frac{B D}{Q M}=\frac{A D}{A M} \cdots(1) \\ \triangle ABD तथा \triangle PQM में
\frac{A B}{P Q}=\frac{B D}{Q M}=\frac{A D}{P M}
भुजा-भुजा-भुजा समरूपता गुणधर्म से
\triangle ABD \sim \triangle PQM \\ \angle B=\angle Q (समरूप त्रिभुजों के संगत कोण बराबर होते हैं)
\triangle ABC तथा \triangle PQR में
\frac{A B}{P Q}=\frac{B C}{Q R} (दिया है)
\angle B=\angle Q [(2) से]
SAS समरूपता गुणधर्म से
\triangle ABC \sim \triangle PQR
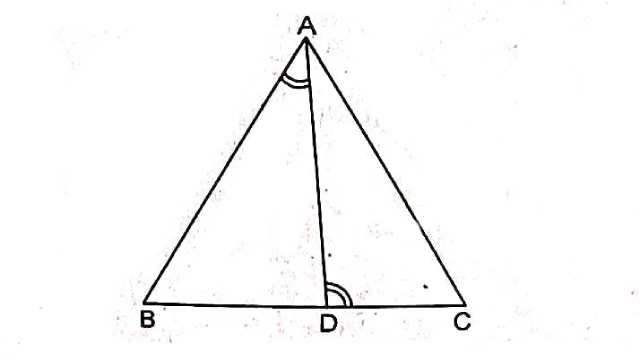
Example:13.एक त्रिभुज ABC की भुजा BC पर एक बिन्दु D इस प्रकार स्थित है कि \angle ADC=\angle BAC है।दर्शाइए कि CA^2=CB \cdot CD है।
Solution:दिया है (Given): \triangle ABC की भुजा BC पर एक बिन्दु D इस प्रकार है कि \angle ADC=\angle BAC
सिद्ध करना है (To Prove): CA^2=CB \cdot CD
उपपत्ति (Proof): \triangle ABC तथा \triangle DAC में
\angle BAC=\angle ADC (दिया है)
\angle C=\angle C (उभयनिष्ठ है)
AA समरूपता गुणधर्म से
\triangle ABC \sim \triangle DAC \\ \Rightarrow \frac{C B}{C A}=\frac{C A}{C D} (समरूप त्रिभुजों की संगत भुजाएँ समानुपाती होती हैं)
\Rightarrow C A^2=CB \cdot CD
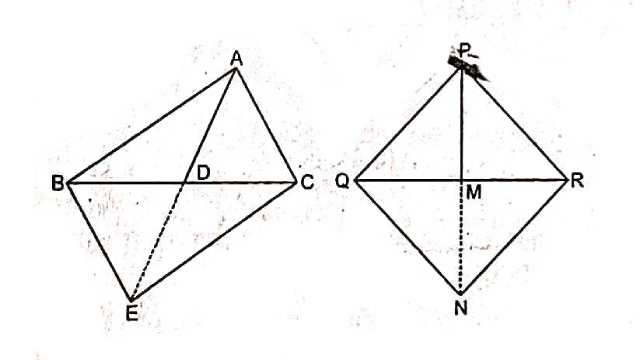
Example:14.एक त्रिभुज ABC की भुजाएँ AB और AC तथा माध्यिका AD एक अन्य त्रिभुज की भुजाओं PQ और PR तथा माध्यिका PM के क्रमशः समानुपाती हैं।दर्शाइए कि \triangle ABC \sim \triangle PQR है।
Solution:दिया है (Given): \triangle ABC और \triangle PQR में \frac{A B}{P Q}=\frac{A C}{P R}=\frac{A B}{P M} तथा D, BC का मध्य बिन्दु है और M, QR का मध्य बिन्दु है।
सिद्ध करना है (To Prove): \triangle ABC \sim \triangle PQR
रचना (Construction):AD को E तक इस प्रकार बढ़ाया कि AD=DE हो।BE और CE को मिलाया।PM को N तक बढ़ाया ताकि PM=MN हो।QN और NR को मिलाया।
उपपत्ति (Proof):चतुर्भुज ABEC के विकर्ण AE और BC परस्पर D बिन्दु पर समद्विभाजित करते हैं।
चतुर्भुज ABEC एक समान्तर चतुर्भुज है।
अतः BE=AC (समान्तर चतुर्भुज की सम्मुख भुजाएँ बराबर होती हैं)
इसी प्रकार PQNR भी एक समान्तर चतुर्भुज है।
QN=PR (समान्तर चतुर्भुज की सम्मुख भुजाएँ बराबर होती है)
\frac{A B}{P G}=\frac{A C}{P R}=\frac{A D}{D M}(दिया है)
\Rightarrow \frac{A B}{P Q}=\frac{B E}{Q N}=\frac{2 A D}{2 P M} [(1) व (2) से]
\Rightarrow \frac{A B}{P Q}=\frac{B E}{Q N}=\frac{A E}{P N} \cdots(3) \\ \triangle ABE तथा \triangle PQN में
\frac{A B}{P Q}=\frac{B E}{Q N}=\frac{A E}{P N} [ (3) से]
SSS समरूपता गुणधर्म से
\triangle ABE \sim \triangle PQN \\ \angle BAE=\angle QPN (समरूप त्रिभुजों के संगत कोण बराबर होते हैं)…..(4)
इसी प्रकार \triangle AEC \sim \triangle PNR \\ \therefore \angle EAC=\angle NPR \cdots(5)
समीकरण (4) व (5) को जोड़ने परः
\angle BAE+\angle EAC=\angle QPN+\angle NPR \\ \Rightarrow \angle BAC=\angle QPR \cdots(6)
अब \triangle ABC तथा \triangle PQR में
\frac{A B}{P Q}=\frac{A C}{P R} (दिया है)
\angle BAC=\angle QPR [(6) से]
SAS समरूपता गुणधर्म से
\triangle ABC \sim \triangle PQR
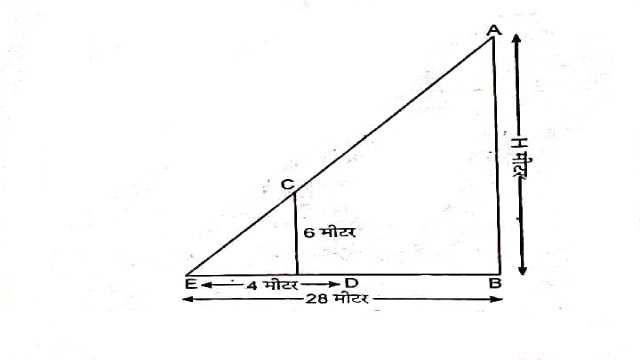
Example:15.लम्बाई 6m वाले एक उर्ध्वाधर स्तम्भ की भूमि पर छाया की लम्बाई 4m है जबकि उसी समय एक मीनार की छाया की लम्बाई 28m है।मीनार की ऊँचाई ज्ञात कीजिए।
Solution:स्तम्भ CD की लम्बाई=6 मीटर
स्तम्भ CD की छाया DE=4 मीटर
माना मीनार AB की ऊँचाई=h मीटर
मीनार AB की छाया BE=28 मीटर
\triangle CDE तथा \triangle ABE में
\angle E=\angle E (उभयनिष्ठ है)
\angle CDE=\angle ABE (संगत कोण)
\angle DCE=\angle BAE (संगत कोण)
AAA समरूपता गुणधर्म से
\triangle CDE \sim \triangle ABE \\ \frac{A B}{C D}=\frac{B E}{D E} \\ \Rightarrow \frac{h}{6}= \frac{28}{4} \\ \Rightarrow h=\frac{28}{4} \times 6 \\ \Rightarrow h=42 मीटर
Example:16.AD और PM त्रिभुजों ABC और PQR की क्रमशः माध्यिकाएँ हैं। \triangle ABC \sim \triangle PQR है। सिद्ध कीजिए कि \frac{A B}{P Q}=\frac{A D}{P M} है।
Solution: दिया है (Given): AD और PM ,\triangle ABC और \triangle PQR कि माध्यिकाएँ हैं। तथा \triangle ABC \sim \triangle PQR
सिद्ध करना है (To Prove): \frac{A B}{P Q}=\frac{A D}{P M}
उपपत्ति (Proof): \triangle ABC \sim \triangle PQR \\ \frac{A B}{P Q}=\frac{B C}{Q R} (समरूप त्रिभुजों की भुजाएँ समानुपाती होती हैं)
AD, \triangle ABC की माध्यिका है
\therefore BD=\frac{1}{2} BC \Rightarrow BC=2 BD \cdots(2)
AD, \triangle PQR की माध्यिका है
\therefore QM=\frac{1}{2} QR \Rightarrow QR=2 QM \cdots(3)
समीकरण (1),(2) व (3) सेः
\frac{A B}{P G}=\frac{2 B D}{2 Q M} \\ \Rightarrow \frac{A B}{P G}=\frac{B D}{Q M} \cdots(4) \\ \triangle ABD तथा \triangle PQM में
\frac{A B}{P Q}=\frac{B D}{Q M} [(4) से]
\angle B=\angle Q \quad[\because \triangle ABC \sim \triangle PQR]
SAS समरूपता गुणधर्म से
\triangle ABD \sim \triangle PQM \\ \frac{A B}{P Q}=\frac{A D}{PM} (समरूप त्रिभुजों की भुजाएँ समानुपाती होती हैं)
उपर्युक्त उदाहरणों के द्वारा त्रिभुजों की समरूपता कक्षा 10 (Similarity of Triangles Class 10),त्रिभुजों की समरूपता के लिए कसौटियाँ कक्षा 10 (Criteria for Similarity of Triangles Class 10) को समझ सकते हैं।
3.त्रिभुजों की समरूपता कक्षा 10 पर आधारित सवाल (Questions Based on Similarity of Triangles Class 10):
(1.)चित्र में यदि EF \parallel BC तथा GE \parallel DC हो तो सिद्ध कीजिए किः \frac{A G}{A D}=\frac{A F}{A B}
(2.)सिद्ध कीजिए कि समलम्ब चतुर्भुज की समान्तर भुजाओं के समान्तर खींची गई रेखा असमान्तर भुजाओं को समान अनुपात में विभाजित करती है।
(3.)सिद्ध कीजिए कि दो समरूप त्रिभुजों के परिमापों का अनुपात किन्हीं दो संगत भुजाओं के अनुपात के समान होता है।
उपर्युक्त सवालों को हल करने पर त्रिभुजों की समरूपता कक्षा 10 (Similarity of Triangles Class 10),त्रिभुजों की समरूपता के लिए कसौटियाँ कक्षा 10 (Criteria for Similarity of Triangles Class 10) को समझ सकते हैं।
Also Read This Article:-Tangent to Circle Class 10
4.त्रिभुजों की समरूपता कक्षा 10 (Frequently Asked Questions Related to Similarity of Triangles Class 10),त्रिभुजों की समरूपता के लिए कसौटियाँ कक्षा 10 (Criteria for Similarity of Triangles Class 10) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.RHS त्रिभुजों की समरूपता कसौटी क्या है? (What is RHS Criteria for Similarity of Triangles?):
उत्तर:यदि दो समकोण त्रिभुजों में एक त्रिभुज का कर्ण तथा एक भुजा,दूसरे त्रिभुज के कर्ण तथा एक भुजा के समानुपाती हो तो दोनों त्रिभुज समरूप होते हैं।इसे RHS समरूपता कसौटी कहा जा सकता है।
प्रश्न:2.समरूपता का व्यावहारिक जीवन में क्या महत्त्व है? (What is Importance of Similarity in Practical Life?):
उत्तर:समरूपता के गुण का व्यावहारिक जीवन में अत्यन्त महत्त्व है।समरूपता के गुण का उपयोग डिजाइन इन्जीनियर और आर्किटेक्ट किया करते हैं।किसी भवन या कलपुर्जों का किसी पैमाने के हिसाब से समरूप डिजाइन बनाते हैं जो आकार (size) में भवन या कलपुर्जे से काफी छोटा होता है,ठेकेदार या कारीगर उसे समझकर सही-सही भवन निर्माण कर लेता है।
समरूप आकृतियों के विभिन्न भागों में एकैकी संगतता (One to One Correspondence) होती है।समरूप आकृतियों के संगत भाग समानुपाती होते हैं।
प्रश्न:3.ज्यामिति में प्रमेय को सिद्ध करने के लिए किन चरणों का प्रयोग किया जाता है? (Which Steps are Used to Prove the Theorem in Geometry?):
उत्तर:प्रमेय (Theorem) तथा निर्मेयों (Problem) का अध्ययन आगमनिक,निगमनिक तथा वैश्लेषिक (Analytic) विधि से किया जाता है।इस विधि में प्रत्येक प्रमेय को क्रमागत पदों में लिखा जाता है,प्रत्येक कथन की सत्यता के लिए आवश्यक प्रमाण दिए जाते हैं।ज्यामिति में किसी प्रमेय को सिद्ध करने के लिए निम्नलिखित चरणों का उपयोग किया जाता हैः
(1.)सर्वप्रथम प्रमेय लिखते हैं जो कि एक सामान्य कथन के रूप में होता है।इस कथन का एक भाग परिकल्पना और दूसरा भाग निष्कर्ष होता है।
(2.)परिकल्पना के अनुसार आकृति बनाई जाती है।
(3.)”दिया हुआ है” (Given) शीर्षक के अन्तर्गत प्रमेय की परिकल्पना को आकृति द्वारा स्पष्ट करके लिखा जाता है।
(4.)”सिद्ध करना है” (To Prove) शीर्षक के अन्तर्गत प्रमेय के निष्कर्ष को जो कि हमें सिद्ध करना होता है,आकृति के अनुसार लिखा जाता है।
(5.)”रचना” (Construction) शीर्षक के अन्तर्गत,प्रमेय को सिद्ध करने हेतु कोई आवश्यक रचना करनी हो तो उसे आकृतिनुसार स्पष्टतया लिखा जाता है।
(6.)”उपपत्ति” (Proof) शीर्षक के अन्तर्गत क्रमशः कथन और कारण स्पष्ट करते हुए प्रमेय को चरणबद्ध तरीके से सिद्ध किया जाता है।अन्त में जब प्रमेय सिद्ध हो जाता है तो Q.E.D. (quod erat demonstrandum) या इतिसिद्धम अंकित किया जाता है जिसका अर्थ है कि प्रमेय सिद्ध किया जा चुका है।
उपर्युक्त प्रश्नों के उत्तर द्वारा त्रिभुजों की समरूपता कक्षा 10 (Similarity of Triangles Class 10),त्रिभुजों की समरूपता के लिए कसौटियाँ कक्षा 10 (Criteria for Similarity of Triangles Class 10) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Similarity of Triangles Class 10
त्रिभुजों की समरूपता कक्षा 10
(Similarity of Triangles Class 10)
Similarity of Triangles Class 10
त्रिभुजों की समरूपता कक्षा 10 (Similarity of Triangles Class 10) में दो त्रिभुज समरूप
होते हैं यदि उनकी संगत भुजाएँ एक ही अनुपात में हों या उनके संगत कोण बराबर हों
अथवा दो भुजाएँ एक ही
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.