1.त्रिभुजों की समरूपता (Similarity of Triangles),समरूप त्रिभुज (Similar Triangles)-

त्रिभुजों की समरूपता (Similarity of Triangles) को समझने के लिए समरूपता को समझना आवश्यक है।
समरूपता (Similarity)-दो आकृतियां समान हों परन्तु माप समान न हों समरूप आकृतियां कहलाती हैं।दो सर्वांगसम आकृतियां समरूप होती है परन्तु दो समरूप आकृतियां सर्वांगसम नहीं होती है।जैसे-दो रेखाएं समरूप होती हैं?,दो वृत्त समरूप होते हैं?,दो समबाहु त्रिभुज भी समरूप होते हैं।
सर्वांगसमता (Congruence):दो ज्यामितीय आकृतियां सर्वांगसम तब कहे जाते हैं जब उनके आकार तथा माप समान हों।
त्रिभुजों की समरूपता के गुणधर्म (Similarity of Triangles Properties)1:
त्रिभुजों की समरूपता प्रमेय (Similarity of Triangles Theorem),समरूप त्रिभुज प्रमेय (Similar Triangles Theorem):1.कोण-कोण-कोण समरूपता (AAA Similarity Property)
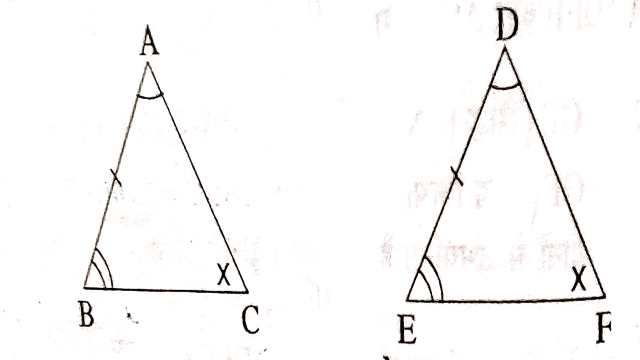
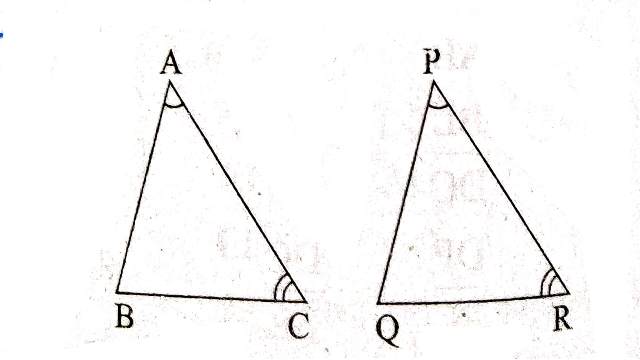
यदि दो त्रिभुजों के संगत कोण बराबर हों अर्थात् दो त्रिभुज समान कोणिक (Equiangular) हों तो त्रिभुज परस्पर समरूप होते हैं।

दिया है (Given):\triangle ABC तथा \triangle DEF  इस प्रकार हैं कि \angle A=\angle D,\angle B=\angle E तथा \angle C=\angle F
सिद्ध करना है (To Prove):\triangle ABC \sim \triangle DEF
प्रथम स्थिति (Case I):जब AB=DE
उपपत्ति (Proof): \triangle ABC और \triangle DEF में

\angle A=\angle D \\ \angle B=\angle E
AB=DE
कोण-कोण-कोण सर्वांगसमता गुणधर्म से (By AAA Congruence Property)

\triangle ABC \cong \triangle DEF
\Rightarrow BC=EF,AC=DF (सर्वांगसम त्रिभुजों की संगत भुजाएं बराबर होती है)
AB=DE

\Rightarrow \frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}
द्वितीय स्थिति (Case II):जब AB<DE हो
इस स्थिति में हम DE पर एक बिन्दु P तथा DF पर बिन्दु  Q तक इस प्रकार बढ़ाते हैं कि DP=AB,DQ=AC तथा P और Q को मिलाते हैं।

उपपत्ति (Proof): \triangle ABC और \triangle DPQ में
AB=DP

\angle A=\angle D
AC=DQ
भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से (SAS Congruence Property)

\triangle ABC \cong \triangle DPQ \\ \Rightarrow \angle ABC=\angle DPQ.....(1)

तथा \angle ACB=\angle DQP.....(2)
(सर्वांगसम त्रिभुजों के संगत कोण बराबर होते हैं)
\angle B=\angle E (दिया है)…..(3)

\angle C=\angle F (दिया है)…..(4)
(1),(2),(3) तथा (4) से-

\Rightarrow \angle DPQ=\angle DEF (संगत कोण)…..(5)

तथा \angle DQP=\angle DFE (संगत कोण)…..(6)
(3) में संगत कोण बराबर हैं अतः PQ \parallel EF
\triangle DEF में थेल्स प्रमेय से-

\Rightarrow \frac{DP}{DE}=\frac{DQ}{DF}
DP=AB तथा DQ=AC

\Rightarrow \frac{AB}{DE}=\frac{AC}{DF}.....(7)
इसी प्रकार हम सिद्ध कर सकते हैं कि

\frac{AB}{DE}=\frac{BC}{EF}.....(8)
( 7) तथा (8) से-

\Rightarrow \frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}
संगत भुजाएं समानुपाती हैं अतः

\triangle ABC \sim \triangle DEF

तृतीय स्थिति (Case III):जब AB>DE हो
इस स्थिति में हम \triangle DEF की भुजाओं DE तथा EF को क्रमशः P तथा Q तक इस प्रकार बढ़ाते हैं कि DP=AB,DQ=AC तथा PQ को मिलाते हैं।

उपपत्ति (Proof): \triangle ABC और \triangle DPQ में
AB=DP
AC=DQ

\angle A=\angle D
भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से (SAS Congruence Property)

\triangle ABC \cong \triangle DPQ
(सर्वांगसम त्रिभुजों के संगत कोण बराबर होते हैं)…..(1)
\angle B=\angle E (दिया है)......(2)
(1) तथा (2) से-

\angle DPQ=\angle DEF.....(3)
(3) में संगत कोण बराबर हैं

\therefore PQ \parallel EF
\triangle DPQ में थेल्स प्रमेय से-

\Rightarrow \frac{DE}{DP}=\frac{DF}{DQ}
DP=AB तथा DQ=AC (रचना से)

\Rightarrow \frac{DE}{AB}=\frac{DF}{AC} \\ \Rightarrow \frac{AB}{DE}=\frac{AC}{DF}.....(4)
इसी प्रकार हम सिद्ध कर सकते हैं कि

\frac{AB}{DE}=\frac{BC}{EF}......(5)
( 4) तथा (5) से-

\frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}
संगत भुजाएं समानुपाती हैं अतः

\triangle ABC \sim \triangle DEF
उपप्रमेय (Corollary):यदि एक त्रिभुज के दो कोण, दूसरे त्रिभुज के संगत दो कोणों के बराबर हो तो दोनों त्रिभुज समरूप होंगे।
त्रिभुजों की समरूपता गुणधर्म (Similarity of Triangles Properties):2.
त्रिभुजों की समरूपता प्रमेय (Similarity of Triangles Theorem),समरूप त्रिभुज प्रमेय (Similar Triangles Theorem):2.भुजा-भुजा-भुजा समरूपता (SSS Similarity)
यदि दो त्रिभुजों की संगत भुजाएं समानुपाती हों तो ये त्रिभुज परस्पर समरूप होते हैं।

दिया है (Given):\triangle ABC तथा \triangle DEF में

\frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}
सिद्ध करना है (To Prove):\triangle ABC \sim \triangle DEF
रचना (Construction):\triangle DEF की भुजाओं DE तथा DF (या DE और DF बढ़ी हुई) पर क्रमशः बिन्दु P तथा Q इस प्रकार लें कि DP=AB तथा DQ=AC,बिन्दु P तथा Q को मिलाइए।
उपपत्ति (Proof):\frac{AB}{DE}=\frac{AC}{DF}(दिया है)
तथा DP=AB (रचना से)
DQ=AC (रचना से)

\Rightarrow  \frac{DP}{DE}=\frac{DQ}{DF}
थेल्स प्रमेय से PQ \parallel EF
\Rightarrow \angle DPQ=\angle E (संगत कोण)
\angle DQP=\angle F (संगत कोण)
कोण-कोण-कोण समरूपता गुणधर्म से (AAA Similarity Property)

\Rightarrow  \triangle DPQ \sim \triangle DEF....(1)
\Rightarrow \frac{DP}{DE}=\frac{PQ}{EF}=\frac{DQ}{DF} (समरूप त्रिभुजों की संगत भुजाएं समानुपाती होती है)
DP=AB
\Rightarrow \frac{AB}{DE}=\frac{PQ}{EF} .....(2) \\ \Rightarrow \frac{AB}{DE}=\frac{BC}{EF} .....(3)  (दिया है)
(2) तथा (3) से-

\frac{PQ}{EF}=\frac{BC}{EF}
\Rightarrow PQ=BC

\triangle ABC तथा \triangle DPQ में
AB=DP (रचना से)
AC=DQ (रचना से)
BC=PQ (सिद्ध किया है)
भुजा-भुजा-भुजा सर्वांगसमता गुणधर्म से (By SSS Congruence Property)

\triangle ABC \cong \triangle DPQ \\ \therefore  \triangle ABC \sim \triangle DPQ.....(4)
(1) तथा (4) से-

\triangle DPQ \sim \triangle ABC \sim \triangle DEF \\ \Rightarrow \triangle ABC \sim \triangle DEF
त्रिभुजों की समरूपता गुणधर्म (Similarity of Triangles Properties):3.
त्रिभुजों की समरूपता प्रमेय (Similarity of Triangles Theorem),समरूप त्रिभुज प्रमेय (Similar Triangles Theorem):3.भुजा-कोण-भुजा समरूपता (SAS Similarity Property)
यदि दो त्रिभुजों में एक त्रिभुज की दो भुजाएं, दूसरे त्रिभुज की संगत दो भुजाओं के समानुपाती हो तथा इनके बीच के कोण दोनों त्रिभुजों में बराबर हो तो ये दोनों त्रिभुज परस्पर समरूप होंगे।

दिया है (Given): \triangle ABC और \triangle DEF में \frac{AB}{DE}=\frac{AC}{DF}  और \angle A=\angle D
सिद्ध करना है (To Prove):\triangle ABC \sim \triangle DEF
रचना (Construction):\triangle DEF में भुजा DE पर बिन्दु P और DF पर बिन्दु Q इस प्रकार लें कि DP=AB और DQ=AC। बिन्दु P और Q को मिलाइए।
उपपत्ति (Proof): \triangle ABC और \triangle DPQ में
AB=DP (रचना से)
AC=DQ (रचना से)
\angle A=\angle D (दिया है)
भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से (By SAS Congruence Property)

\triangle ABC \cong \triangle DPQ \\ \Rightarrow \triangle ABC \sim \triangle DPQ....(1)
\frac{AB}{DE}=\frac{AC}{DF}  (दिया है)
तथा \frac{DP}{DE}=\frac{DQ}{DF}  (रचना से)
थेल्स प्रमेय से PQ \parallel EF
\angle DPQ=\angle E और \angle DQP=\angle F (संगत कोण बराबर होते हैं)
अतः कोण-कोण समरूपता (By AA Similarity Property) के अनुसार

\triangle DPQ \sim \triangle DEF....(2)
(1) व (2) से-

\triangle ABC \sim \triangle DEF
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:-Circle with Tangents

2.त्रिभुजों की समरूपता के उदाहरण (Similarity of Triangles Examples)-

Example-1.दो त्रिभुज ‌ABC और PQR में \frac{AB}{PQ} और \frac{BC}{QR}। दोनों त्रिभुजों में से दो कोणों के नाम बताइए जो बराबर होने चाहिए ताकि ये दोनों त्रिभुज समरूप हो सके।अपने उत्तर के कारण भी बताइए।
Solution–\triangle ABC तथा \triangle PQR में

\angle A=\angle P
तथा \angle C=\angle R होना चाहिए
क्योंकि \angle A +\angle B +\angle C =180^{\circ}
तथा \angle P +\angle Q +\angle R =180^{\circ} \\ \Rightarrow \angle A +\angle B +\angle C=\angle P +\angle Q +\angle R \\ \Rightarrow \angle B =\angle Q   (\because  \angle A=\angle P  तथा \angle C=\angle R)
तो (\angle B =\angle Q  अन्त: कोणों के योग नियम से)
\Rightarrow यदि [katex]\frac{AB}{PQ}=\frac{BC}{QR}
तथा \angle B =\angle Q
भुजा-कोण-भुजा समरूपता गुणधर्म से (SAS Similarity Property)

\Rightarrow \triangle ABC \sim \triangle PQR
Example-2.त्रिभुजों ABC एवं DEF में \angle A =\angle D,\angle B =\angle F  हो तो क्या \triangle ABC \sim \triangle DEF है? अपने उत्तर के लिए कारण दीजिए।
Solution- \triangle ABC व \triangle DEF में
\angle A =\angle D \\  \angle B =\angle F (दिया है)
कोण-कोण समरूपता गुणधर्म से (AA Similarity Property)

\triangle ABC \sim \triangle DEF
\therefore  \triangle ABC व \triangle DEF समरूप नहीं होंगे
\triangle ABC व \triangle DEF समरूप होने के लिए
\angle A =\angle D तथा \angle B =\angle E होना आवश्यक है।
अतः \triangle ABC व \triangle DEF समरूप नहीं है।
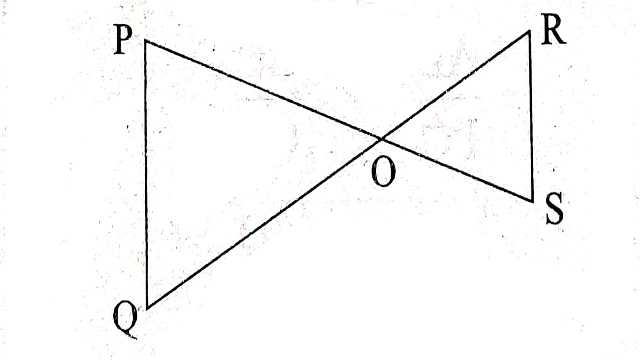
Example-3.आकृति में PQ और RS समान्तर हैं तो सिद्ध कीजिए \triangle POQ \sim \triangle SOQ

Solution-दिया है (Given):PQ \parallel RS
सिद्ध करना है (To Prove): \triangle POQ \sim \triangle SOQ
उपपत्ति (Proof):PQ \parallel RS
\Rightarrow  \angle QPO =\angle RSO (एकान्तर कोण)....(1)
\angle PQO =\angle ORS (एकान्तर कोण)....(2)
\triangle POQ तथा \triangle SOR में
\angle P=\angle S[(1) से]
\angle Q=\angle R [(2) से]
\angle POQ =\angle ROS (शीर्षाभिमुख कोण)
कोण-कोण-कोण समरूपता गुणधर्म से (By AAA Similarity Property)

\triangle POQ \cong \triangle SOR
Example-4.90 सेमी की लम्बाई वाली लड़की बल्ब लगे खम्भे के आधार से परे 1.2 मीटर/सेकण्ड की चाल से चल रही है।यदि बल्ब भूमि से 3.6 मीटर की ऊंचाई पर हो तो 4 सेकण्ड के बाद लड़की की छाया कितने मीटर होगी?
Solution-

माना AB एक बल्ब लगा खम्भा है।तथा एक लड़की है जो 1.2 मीटर/सेकण्ड की चाल से चल रही है तथा 4 सेकण्ड के पश्चात् उसकी स्थिति CD पर है।तथा DE उसकी छाया है।
माना DE=x मीटर
BD=1.2 मीटर × 4=4.8 मीटर
अब \triangle ABE तथा \triangle CDE में

\angle B=\angle D=90^{\circ}
(क्योंकि खम्भा व लड़की दोनों जमीन पर उर्ध्वाधर हैं)
\angle E=\angle E (उभयनिष्ठ कोण)
कोण-कोण समरूपता गुणधर्म से (By AA Similarity Property)

\triangle ABE \sim \triangle CDE
अतएव \frac{BE}{DE}=\frac{AB}{CD} \\ \frac{4.8+x}{x}=\frac{3.6}{0.9}
[90 सेमी=\frac{90}{100} मीटर=0.9 मीटर]

\Rightarrow \frac{4.8+x}{x}=\frac{4}{1} \\ \Rightarrow 4.8+x=4x \\ \Rightarrow 4x-x=4.8 \\ \Rightarrow 3x=4.8 \\ \Rightarrow x=1.6 मीटर
4 सेकण्ड के बाद लड़की की छाया 1.6 मीटर होगी।
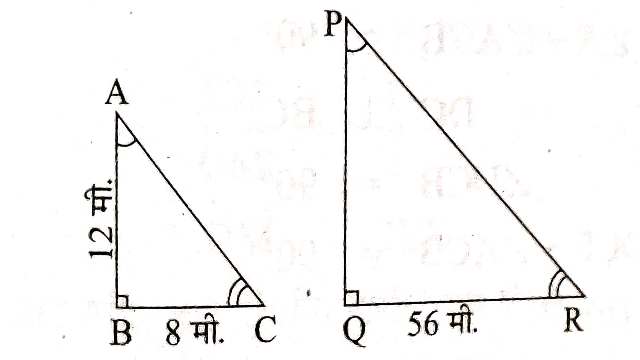
Example-5.12 मीटर लम्बाई वाले उर्ध्वाधर स्तम्भ की भूमि पर छाया की लम्बाई 8 मीटर है,उसी समय एक मीनार की छाया की लम्बाई 56 मीटर हो तो मीनार की ऊंचाई ज्ञात कीजिए।

Solution-उर्ध्वाधर स्तम्भ की ऊंचाई=12 मीटर
स्तम्भ की छाया की लम्बाई=8 मीटर
माना की मीनार की ऊंचाई=h मीटर
मीनार की छाया की लम्बाई=56 मीटर
\triangle ABC और \triangle PQR में
\angle C=\angle R(मीनार व स्तम्भ की छाया के कोण)

\angle B=\angle Q=90^{\circ}
कोण-कोण समरूपता गुणधर्म से (By AA Similarity Property)

\triangle ABC \sim \triangle PQR \\ \frac{AB}{PQ}=\frac{BC}{QR}
(त्रिभुज समरूप हो तो भुजाएं समानुपाती होती है)

\frac{12}{h}=\frac{8}{56} \\ \Rightarrow h \times 8=12 \times 56 \\ \Rightarrow h=\frac{12 \times 56}{8} \\  \Rightarrow h=84 मीटर
अतः मीनार की ऊंचाई 84 मीटर है।
Example-6.किसी त्रिभुज के शीर्ष A से उसकी सम्मुख भुजा BC पर लम्ब डालने पर {AD}^{2}=BD \times DC प्राप्त होता है तो सिद्ध कीजिए \triangle ABC एक समकोण त्रिभुज है।
Solution-दिया है (Given):\triangle ABC के शीर्ष A से उसकी सम्मुख BC पर लम्ब AD इस प्रकार है कि {AD}^{2}=BD \times DC

सिद्ध करना है (To Prove):\triangle ABC समकोण त्रिभुज है।
उपपत्ति (Proof): {AD}^{2}=BD \times DC (दिया है)

\frac{BD}{AD}=\frac{DA}{DC}
\triangle BDA तथा \triangle ADC में
\frac{BD}{AD}=\frac{DA}{DC} (दिया है)

\angle BDA=\angle ADC=90^{\circ}
भुजा-कोण-भुजा समरूपता गुणधर्म से (By SAS Similarity Property)

\triangle BDA \sim \triangle ADC \\ \angle ABD=\angle CAD.....(1)
तथा \angle ACD=\angle BAD.....(2)
[समरूप त्रिभुजों के संगत कोण बराबर होते हैं]
(1) और (2) को जोड़ने पर-

\angle ABD +\angle ACD=\angle CAD+ \angle BAD \\ \therefore \angle ABD +\angle ACD=\angle BAC \\ \angle B+\angle C=\angle A
दोनों पक्षों में \angle A जोड़ने पर-

\angle A+\angle B+\angle C=\angle A+\angle A \\  \Rightarrow 180^{\circ}=2 \angle A (त्रिभुज के अन्त: कोणों का योग)

2 \angle A=180^{\circ} \\\Rightarrow \angle A=90^{\circ}
\triangle ABC एक समकोण त्रिभुज है।
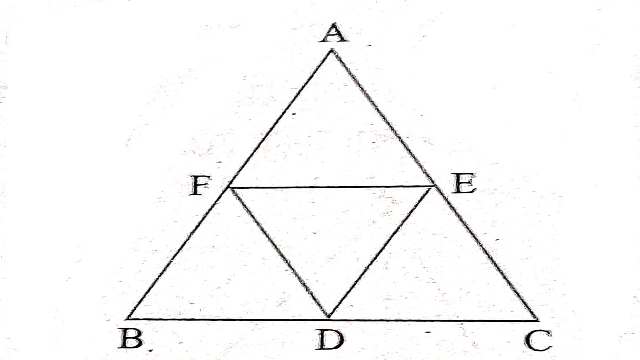
Example-7.सिद्ध कीजिए किसी त्रिभुज की तीनों भुजाओं के मध्य बिन्दुओं को क्रमशः मिलाने पर बनने वाले चारों त्रिभुज अपने मूल त्रिभुज के समरूप होते हैं।

Solution-दिया है (Given):\triangle ABC  जिसमें D,E तथा F क्रमशः BC,CA तथा AB के मध्य बिन्दु हैं।
सिद्ध करना है (To Prove):\triangle AFE , \triangle FBD , \triangle EDC तथा \triangle DEF , \triangle ABC के समरूप हैं।
उपपत्ति (Proof): \triangle AFE तथा \triangle ABC में F तथा E क्रमशः AB तथा AC के मध्य बिन्दु हैं।
FE \parallel BC \\ \angle AFE=\angle B(संगत कोण)....(1)
\angle AEF=\angle C(संगत कोण).....(2)
\triangle AFE तथा \triangle ABC में
\angle AFE=\angle B [(1) से]
\angle AEF=\angle C [(2) से]
\angle A=\angle A (उभयनिष्ठ कोण)
कोण-कोण-कोण समरूपता गुणधर्म से (By AAA Similarity Property)

\triangle AFE \sim \triangle ABC
इसी प्रकार हम सिद्ध कर सकते हैं कि
\triangle FBD \sim \triangle ABC और

\triangle EDC \sim \triangle ABC
अब \triangle DEF तथा \triangle ABC में
EF \parallel BD तथा DE \parallel BF
BDEF एक समान्तर चतुर्भुज होगा
\angle FED=\angle B (समान्तर चतुर्भुज के सम्मुख कोण).....(3)

EF \parallel DC \\ DF \parallel CE
CDFE समान्तर चतुर्भुज है
\angle DFE=\angle C  (समान्तर चतुर्भुज के सम्मुख कोण)....(4)
\triangle DEF तथा \triangle ABC में

\angle FED=\angle B \\ \angle DFE=\angle C
कोण-कोण समरूपता गुणधर्म से (By AA Similarity Property)

\triangle ABC \sim \triangle DEF
इसी प्रकार \triangle AFE , \triangle FBD , \triangle DEF तथा \triangle EDC चारों त्रिभुज, \triangle ABC के समरूप हैं।
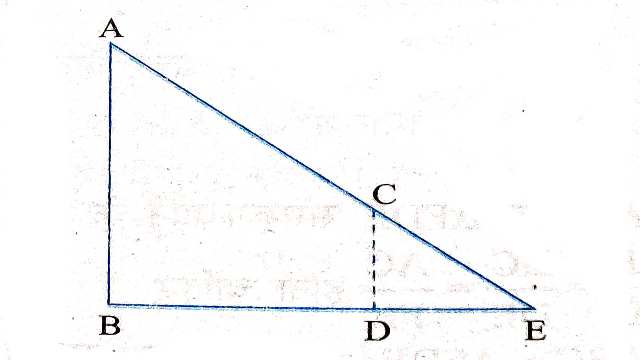
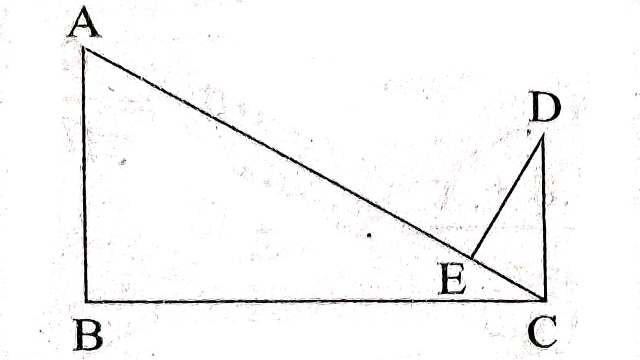
Example-8.आकृति में दर्शाए अनुसार यदि AB \perp BC, DC \perp BC और DE \perp AC हो तो सिद्ध कीजिए \triangle CED \sim \triangle ABC है।

Solution-दिया है (Given):AB \perp BC, DC \perp BC तथा DE \perp AC
सिद्ध करना है (To Prove): \triangle CED \sim \triangle ABC
उपपत्ति (Proof):AB \perp BC \\ \angle ABC=90^{\circ}
\triangle ABC में

\angle A + \angle B +\angle ACB=180^{\circ} \\ \therefore \angle A + 90^{\circ} +\angle ACB=180^{\circ} \\ \angle A +\angle ACB=90^{\circ}.....(1) \\ DC \perp BC \\  \angle DCB=90^{\circ} \\ \angle DCE +\angle ACB=90^{\circ}....(2)
(1) और (2) से-

\angle A +\angle ACB=\angle DCE+\angle ACB \\ \angle A =\angle DCE....(3)
अब \triangle ABC तथा \triangle CED में
\angle ABC=\angle CED=90^{\circ}

\angle A =\angle DCE[(3) से]
कोण-कोण समरूपता गुणधर्म से (By AA Similarity Property)
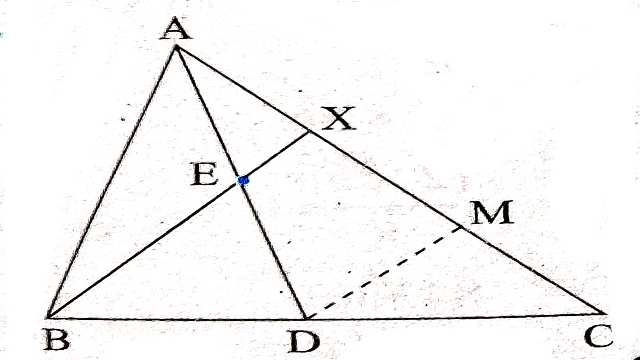
Example-9. \triangle ABC  की भुजा BC के मध्य बिन्दु D है।यदि AD का समद्विभाजन करती हुई एक रेखा B से इस प्रकार खींची जाए कि वह भुजा AD को E पर काटते हुए AC को X पर काटे तो सिद्ध कीजिए कि \frac{EX}{BE}=\frac{1}{3} है।
Solution-दिया है (Given):\triangle ABC में D बिन्दु भुजा BC का मध्य बिन्दु है तथा E,AD का मध्य बिन्दु है।

सिद्ध करना है (To Prove):\frac{EX}{BE}=\frac{1}{3}
रचना (Construction):DM \parallel BX  खींचा।
उपपत्ति (Proof): EX \parallel DM और AM तिर्यक रेखा है तो
\angle AXE=\angle AMD(संगत कोण)....(1)
\triangle AEX तथा \triangle ADM में
\angle AXE=\angle AMD[(1) से]
\angle EAX=\angle MAD(उभयनिष्ठ कोण)
कोण-कोण समरूपता गुणधर्म से (By AA Similarity Property)
\frac{EX}{DM}=\frac{AE}{AD} \\ \frac{EX}{DM}=\frac{AE}{2 AE} (E,AD का मध्य बिन्दु है)

\frac{EX}{DM}=\frac{1}{2}
DM=2 EX.....(2)
और XC तिर्यक रेखा है
\angle CMD=\angle CXB (संगत कोण).....(3)
\triangle CMD और \triangle CXB में
\angle CMD=\angle CXB[(3) से]
\angle C=\angle C(उभयनिष्ठ कोण)
कोण-कोण समरूपता गुणधर्म से (By AA Similarity Property)

\triangle CMD \sim \triangle CXB

\frac{PM}{BX}=\frac{CD}{CB} \\ \frac{DM}{BX}=\frac{CD}{2 CD}=\frac{1}{2} ( \because CB=2 CD)
\frac{2 EX}{BX}=\frac{1}{2} [(2) से]
BX=4 EX
BE+EX=4 EX
BE=3 EX

\frac{EX}{BE}=\frac{1}{3}
उपर्युक्त उदाहरणों के द्वारा त्रिभुजों की समरूपता (Similarity of Triangles),समरूप त्रिभुज (Similar Triangles) को समझ सकते हैं।

3.त्रिभुजों की समरूपता की समस्याएं (Similarity of Triangles Problems),त्रिभुजों की समरूपता के सवाल (Similarity of Triangles Questions)-

(1.)एक 12 सेमी उर्ध्वाधर छड़ की जमीन पर छाया की लम्बाई 8 सेमी है।यदि इसी समय एक मीनार की छाया की लम्बाई 40 मीटर हो तो मीनार की ऊंचाई होगी।
(2.) \triangle ABC में D,BC पर कोई बिन्दु इस प्रकार है कि \frac{AB}{AC} =\frac{BD}{DC} एवं \angle B=70^{\circ} , \angle C=50^{\circ}  हो तो \angle BAD ज्ञात कीजिए।
(3.) \triangle ABC की भुजा BC पर एक बिन्दु D इस प्रकार है कि \angle ADC=\angle BAC तो सिद्ध कीजिए कि {AC}^2=BC \times DC
(4.)यदि एक समकोण त्रिभुज में समकोण बनाने वाले शीर्ष से कर्ण पर लम्ब डाला जाए तो सिद्ध कीजिए कि इस लम्ब के दोनों ओर बने त्रिभुज परस्पर समरूप होंगे तथा ये दोनों त्रिभुज उस मूल त्रिभुज के भी समरूप होंगे जिसके ये दोनों भाग हैं।
उत्तर (Answers):
(1.)60 मीटर (2) \angle BAD=30^{\circ}
उपर्युक्त सवालों को हल करने पर त्रिभुजों की समरूपता (Similarity of Triangles),समरूप त्रिभुज (Similar Triangles) को ठीक से समझा जा सकता है।

Also Read This Article:-Basic Proportionality Theorem

4.त्रिभुजों की समरूपता (Similarity of Triangles) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न-

उपर्युक्त प्रश्नों के उत्तर द्वारा त्रिभुजों की समरूपता (Similarity of Triangles),समरूप त्रिभुज (Similar Triangles) को भली-भांति समझ सकते हैं।

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Instagram	click here
4.	Linkedin	click here
5.	Facebook Page	click here