1.अन्तर संकारकों के सम्बन्ध (Relations of Difference Operators),परिमित अन्तर कलन (Calculus of Finite Differences):

Relations of Difference Operators

अन्तर संकारकों के सम्बन्ध (Relations of Difference Operators) तथा परिमित अन्तर कलन पर आधारित सवालों को हल करके समझने का प्रयास करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:- Simpson Rule in Numerical Analysis

2.अन्तर संकारकों के सम्बन्ध के उदाहरण (Relations of Difference Operators Illustrations):

Illustration:1.निम्न आँकड़ों के लिए अग्रान्तर सारणी बनाइए:
(Construct a forward difference table for the following data):
Illustration:1(i).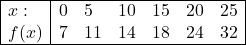
Solution:अग्रान्तर सारणी (Forward Difference Table)

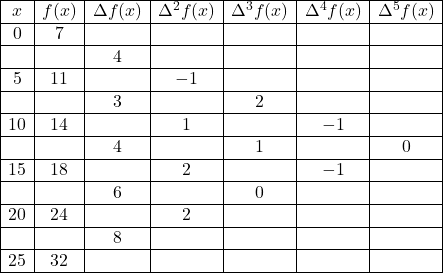
Illustration:1(ii).
Solution:अग्रान्तर सारणी (Forward Difference Table)

Illustration:2.निम्न का मान ज्ञात कीजिए।
(Evaluate the following):
Illustration:2(iv). $\Delta a b^{c x}, h=1$
Solution: $\Delta a b^{c x}, h=1 \\ \Delta a b^{c x} =a b^{c(x+h)}-a b^{c x} \\ =a b^{c x+c h}-a b^{c x} \\ =a b^{c x} \cdot b^{c h}-a b^{c x} \\ =a b^{c x}\left(b^{c h}-1\right) \\ \Rightarrow \Delta a b^{c x} =a b^{c x}\left(b^c-1\right), h=1$
Illustration:2(viii). $\Delta(\log x)$
Solution: $\Delta(\log x) \\ \Delta(\log x) =\log (x+h)-\log x \\=\log \left(\frac{x+h}{x}\right) \\ \Rightarrow \Delta(\lg x) =\log \left(1+\frac{h}{x}\right)$
Illustration:2(ix).$\nabla\left(x^2+2 x\right)$
Solution: $\nabla \left(x^2+2 x\right) \\ \nabla y_x=y_x-y_{x-h} \\ \nabla\left(x^2+2 x\right)=x^2+2 x-\left[(x-h)^2+2(x-h)\right] \\ =x^2+2 x-\left(x^2-2 h x+h^2+2 x-2 h\right) \\ =x^2+2 x-x^2+2 h x-h^2-2 x+2 h \\ \Rightarrow \nabla \left(x^2+2 x\right)=2 h x+2 h-h^2$
Illustration:4.मान ज्ञात कीजिए (Evaluate):
Illustration:4(i). $\Delta^2\left(3 e^x\right)$
Solution: $\Delta^2\left(3 e^x\right) \\ \Delta^2\left(3 e^x\right) =(E-1)^2\left(3 e^x\right) \\ =\left(E^2-2 E+1\right)\left(3 e^x\right) \\ =E^2\left(3 e^x\right)-2 E\left(3 e^x\right)+3 e^x \\ =3 e^{x+2 h}-6 e^{x+h}+3 e^x \\=3 e^x\left(e^{2 h}-2 e^h+1\right) \\ \Rightarrow \Delta^2\left(3 e^x\right) =3 e^x\left(e^h-1\right)^2$
Illustration:4(ii). $\Delta^2(\cos 2 x)$
Solution: $\Delta^2(\cos 2 x) \\ \Delta^2(\cos 2 x)=(E-1)^2(\cos 2 x) \\ =\left(E^2-2 E+1\right)(\cos 2 x) \\ =E^2(\cos 2 x)-2 E(\cos 2 x)+\cos 2 x \\ =\cos 2(x+2 h)-2 \cos 2(x+h)+\cos 2 x \\ =\cos (2 x+4 h)-2 \cos (2 x+2 h)+\cos 2 x \\ =[\cos (2 x+4 h)+\cos 2 x]-2 \cos (2 x+2 h) \\ =2 \cos \left(\frac{2 x+4 h+2 x}{2}\right) \cos \left(\frac{2 x+4 h-2 x}{2}\right) -2 \cos (2 x+2 h) \\ =2 \cos (2 x+2 h) \cos 2 h-2 \cos (2 x+2 h) \\=2 \cos (2 x+2 h)(\cos 2 h-1) \\ =2 \cos (2 x+2 h)\left(1-2 \sin ^2 h-1\right) \\ =-4 \sin ^2 h \cos (2 x+2 h) \\ \Rightarrow \Delta^2(\cos 2 x)=-4 \sin ^2 h \cos (2 x+2 h)$
Illustration:4(iv). $\Delta^4\left(a e^x\right)$
Solution: $\Delta^4\left(a e^x\right) \\ \Delta^4\left(a e^x\right)=(E-1)^4\left(a e^x\right) \\ =\left(E^4-4 E^3+6 E^2-4 E+1\right)\left(a e^x\right) \\ =a\left(E^4 e^x-4 E^3 e^x+6 E^2 e^x-4 E e^x+e^x\right) \\ =a\left(e^{x+4 h}-4 e^{x+3 h}+6 e^{x+2 h}-4 e^{x+h}+e^x\right) \\ =a e^x\left(e^{4 h}-4 e^{3 h}+6 e^{h h}-4 e^h+1\right) \\ =a\left(e^h-1\right)^4 e^x \\ =a(e-1)^4 e^x, h=1 \\ \Rightarrow \Delta^4\left(a e^x\right)=a(e-1)^4 e^x$
Illustration:4(vii). $\left(\frac{\Delta^2}{E}\right) x^2$
Solution: $\left(\frac{\Delta^2}{E}\right) x^2 \\ \Delta^2 E^{-1}\left(x^2\right) \quad\left[\because E^n y_x=y_{x+n h}\right] \\ =\Delta^2(x-h)^2 \\ =\Delta\left[\Delta(x-h)^2\right] \\=\Delta\left[((x+h)-h)^2-(x-h)^2\right] \\ =\Delta\left(x^2-(x-h)^2\right) \\ =\Delta\left(x^2-x^2+2 h x-h^2\right) \\ =\Delta\left(2 h x-h^2\right) \\ =2(x+h) h-h^2-\left(2 h x-h^2\right) \\ \left[\therefore \Delta y_x=y_{x+h}-y _x\right] \\ =2 x h+2 h^2-h^2-2 h x+h^2 \\ \Rightarrow \left(\frac{\Delta^2}{E}\right) x^2=2 h^2$
Illustration:4(viii). $E^n\left(e^x\right)$
Solution: $E^n\left(e^x\right) \\ E^n\left(e^x\right)=e^{x+n h}$
Illustration:5.निम्न के मान ज्ञात कीजिए (Evaluate the following):
Illustration:5(iii). $\Delta^n\left(a b^{cx}\right)$
Solution: $\Delta^n\left(a b^{c x}\right) \\ \Delta\left(a b^{c x}\right) =a b^{c(x+1)}-a b^{c x} \\ =a b^{c x}\left(b^c-1\right) \\ \Delta^2\left(a b^{c x}\right) =\Delta\left[a b^{c x}\left(b^c-1\right)\right] \\ =a b^{c x}\left(b^c-1\right)^2 \\ \ldots \ldots \ldots \ldots \ldots \ldots \\ \ldots \ldots \ldots \ldots \ldots \ldots \\ \Rightarrow \Delta^n\left(a b^{c x}\right)=\left(b^{c}-1\right)^n a b^{c x}$
Illustration:5(iv). $\Delta^n\left[x^{(n)}\right], h=1$
Solution: $\Delta^n\left[x^{(n)}\right], h=1 \\ \Delta x^{(n)}=\left(x+h\right)^{(n)}-x^{(n)} \\ =[(x+h) \cdot(x+h-h)(x+h-2 h) \ldots \ldots \left.\left(x+h-\overline{n-1} \cdot h\right)\right]-\left[x(x-h) \cdots\left(x-\overline{n-1} h\right)\right] \\ =(x+h) x(x-h) \cdots(x-\overline{n-2} h)-(x) (x-h) \cdots(x-\overline{n-2} h)(x-\overline{n-1} h) \\ =x(x-h) \cdots(x-\overline{n-2} h)[(x+h)-(x-\overline{n-1} h)] \\ =x^{(n-1)} \cdot(x+h-x+n h-h) \\ \Delta x^{(n)}=n h\left(x^{n-1}\right) \cdots(1)$
पुनः $\Delta^2 x^{(n)}=\Delta \cdot \Delta x^{(n)} \\ =\Delta\left[n h x^{(n-1)}\right]$ [(1) से]

=$n h \Delta x^{(n-1)} \\ =n h(n-1) h x^{(n-2)} \\ \therefore \Delta^2 x^{(n)}=n(n-1) h^2 x^{(n-2)}$
उपर्युक्त विधि को बार-बार काम में लेने पर:
$\Delta^{n-1} x^{(n)}=n(n-1) \ldots 2 \cdot h^{n-1} x \\ \Delta^n x^{(n)}=n(n-1) \ldots 2 h^{n-1} \Delta x \\ =n(n-1)\ldots 2 h^{n-1}(x+h-x) \\ =n(n-1) \ldots 2+h^n \\ \Rightarrow \Delta^n x^{(n)}=n!h^n \\ \text { put } h=1 \\ \Rightarrow \Delta^n x^{(n)}=n!$
Illustration:6.निम्न के मान ज्ञात कीजिए (Evaluate the following):
Illustration:6(ii). $\Delta^{10}(1-a x) \cdot\left(1-b x^2\right)\left(1-c x^3\right)\left(1-d x^4\right)$
Solution: $\Delta^{10}(1-a x) \cdot\left(1-b x^2\right)\left(1-c x^3\right)\left(1-d x^4\right)$
माना $u_x=(1-a x)\left(1-b x^2\right)\left(1-c x^3\right)\left(1-d x^4\right)$
यहाँ $u_x$, 10 घात का बहुपद है तथा $x^{10}$ का गुणांक (-a)(-b)(-c)(-d) अर्थात् abcd है।
अतः $\Delta^{10} u_x=a bcd(10!)$
[सूत्र $u_x=a x^n+b x^{n-1}+c x^{n-2}+\ldots+l x^2+k x+m \\ \Delta^n u_x=a(n!) h^n$ से]
Illustration:6(iii). $\Delta^n\left(a_0+a_1 x\right)\left(a_1+a_2 x\right)\left(a_2+a_3 x\right)\ldots \left(a_{n-1}+a_n x\right) ;(h=1)$
Solution: $\Delta^n\left(a_0+a_1 x\right)\left(a_1+a_2 x\right)\left(a_2+a_3 x\right)\ldots \left(a_{n-1}+a_n x\right) ;(h=1)$

माना $u_x=\left(a_0+a_1 x\right)\left(a_1+a_2 x\right)\left(a_2+a_3 x\right) \ldots \ldots \left(a_{n-1}+a_n x\right)$
यहाँ $u_x$, n घात का बहुपद है तथा $x^n$  का गुणांक $\left(a_1 a_2 \ldots a_n\right)$  है।
अतः $\Delta^n u_x=\left(a_1 a_2 \ldots a_n\right)(n!)$
[सूत्र $u_x=a x^n+b x^{n-1}+c x^{n-2}+\ldots+l x^2 +k x+m \\ \Delta^n u_x=a(n!) h^n$ से]
Illustration:7.सिद्ध कीजिए कि (Prove that):
Illustration:7(i). $\left(\frac{\Delta^2}{E}\right) x^3=6 x , (if ) h=1$
Solution: $\left(\frac{x^2}{E}\right) x^3=6 x \\ \text { L.H.S.}\left(\frac{\Delta^2}{E}\right) x^3 \\ =\left[\frac{(E-1)^2}{E}\right] x^3 \\ =\left(\frac{E^2-2 E+1}{E}\right) x^3 \\ =\left(E-2+\frac{1}{E}\right) x^3 \\ =\left(E-2+E^{-1}\right) x^3 \\ =E x^3-2 x^3+E^{-1} x^3 \\ =(x+h)^3-2 x^3+(x-h)^3 \\ =x^3+3 x^2 h+3 x h^2+h^3-2 x^2+x^3 -3 x^2 h+3 x h^2-h^3 \\ =2 x^3+6 x h^2-2 x^3 \\ =6 x h^2 \\ \text{put } h=1 \\ =6 x=\text { R.H.S }$
Illustration:7(ii). $\frac{\Delta^2}{E} \sin (x+h)+\frac{\Delta^2 \sin (x+h)}{E \sin (x+h)}=2(\cos h-1) [\sin (x+h)+1]$
Solution: $\frac{\Delta^2}{E} \sin (x+h)+\frac{\Delta^2 \sin (x+h)}{E \sin (x+h)}=2(\cos h-1) [\sin (x+h)+1] \\ \text{L.H.S.} \frac{\Delta^2}{E} \sin (x+h)+\frac{\Delta^2 \sin (x+h)}{E \sin (x+h)} \\ =\frac{(E-1)^2}{E} \sin (x+h)+\frac{(E-1)^2 \sin (x+h)}{E \sin (x+h)} \\ =\left(\frac{E^2-2 E+1}{E}\right) \sin (x+h)+\frac{\left(E^2-2 E+1\right) \sin (x+h)}{E \sin (x+h)} \\ =\left(E-2+E^{-1}\right) \sin (x+h)+ \frac{E^2 \sin (x+h)-2 E \sin (x+h)+\sin (x+h)}{\sin (x+2 h)} \\ =E \sin (x+h)-2 \sin (x+h)+E^{-1} \sin (x+h) +\frac{\sin (x+3 h)-2 \sin (x+2 h)+\sin (x+h)}{\sin (x+2 h)} \\ =\sin (x+2 h)+\sin x-2 \sin (x+h)+\frac{2 \sin (x+2 h) \cos h-2 \sin (x+2 h)}{\sin (x+2 h)} \\ =2 \sin (x+h) \cosh -2 \sin (x+h)+2 \cosh -2 \\ =2 \cosh (\sin (x+h)+1) -2(\sin (x+h)+1) \\ =2(\cos h -1)(\sin (x+h)+1)=\text { R.H.S. }$
Illustration:8.मान ज्ञात कीजिए (Evaluate):
Illustration:8(i). $(\Delta+1)(2 \Delta-1)\left(x^2+2 x+1\right)$
Solution: $(\Delta+1)(2 \Delta-1)\left(x^2+2 x+1\right) \\ =(\Delta+1)\left[2 \Delta\left(x^2+2 x+1\right)-\left(x^2+2 x+1\right)\right] \\ =(\Delta+1) \left[2(x+h)^2+4(x+h)+2-2\left(x^2+2 x+1\right)-\left(x^2+2 x+1\right)\right] \\ =(\Delta+1)\left[2 x^2+4 h x+2 h^2+4 x+4 h+2-3 x^2\right.-6 x-3) \\ =(\Delta+1)\left(-x^2-2 x-1+4 h x+2 h^2+4 h\right) \\ = \Delta\left(-x^2-2 x-1+4 h x+2 h^2+4 h\right)+ \left(-x^2-2 x-1+4 h x+2 h^2+4 h\right) \\ =-(x+h)^2-2(x+h)-1+4 h(x+h)+2 h^2 +4 h-\left(-x^2-2 x-1+4 h x+2 h^2+4 h\right) +\left(-x^2-2 x-1+4 h x+2 h^2+4 h\right) \\= -x^2-2 h x-h^2-2 x-2 h-1+4 h x +4 h^2+2 h^2+4 h \\=-x^2-2 x+2 h x+5 h^2+2 h-1$
Illustration:8(ii). $(E-1)(E-2)\left(2^{\frac{x}{h}}+x\right)$
Solution: $(E-1)(E-2)\left(2^{\frac{x}{h}}+x\right) \\ =(E-1)\left(E 2^{\frac{x}{h}}+E x-2 \cdot 2^{\frac{x}{h}}-2 x\right) \\ =(E-1)\left(2^{2^{\frac{x}{h}+1}}+x+h-2^{\frac{x}{h}+1}-2 x\right) \\ =(E-1)(h-x) \\ =E h-E x-h+x \\ =h-(x+h)-h+x \\ =h-x-h-h+x \\ =-h \\ \Rightarrow (E-1)(E-2)\left(2^{\frac{x}{h}}+x\right)=-h$

Relations of Difference Operators

Illustration:9.अन्तर सारणी बनाकर अनुक्रम 8,12,19,29,42,….. का छठा पद ज्ञात कीजिए।
(By constructing term of sequence 8,12,19,29,42,…..)
Solution:अन्तर सारणी (Difference Table)

y के पाँच मान दिए गए हैं अतः पंचम अन्तर शून्य होना चाहिए

$y_6-58=0 \\ \Rightarrow y_6=58$
Illustration:10.दिया हुआ है कि f(0)=-3,f(1)=6,f(2)=8,f(3)=12 तथा तीसरा अन्तर अचर हो,तो f(6) ज्ञात कीजिए।
(Find f(6),given that f(0)=-3,f(1)=6,f(2)=8,f(3)=12 the third difference being constant.)
Solution:चार मूल्य दिए गए हैं तथा तीसरा अन्तर अचर है अतः चौथा अन्तर शून्य है अर्थात् $\Delta^4 f(x)=0 \\ \Rightarrow(E-1)^4 f(x)=0 \\ \Rightarrow\left(E^4-4 E^3+6 E^2-4 E+1\right) f(x)=0 \\ \Rightarrow E^4 f(x)-4 E^3 f(x)+6 E^2 f(x)-4 E f(x) +f(x)=0 \\ \Rightarrow f(x+4)-4 f(x+3)+6 f(x+2)-4 f(x+1)+f(x)=0 \cdots(1)$
x=0 रखने पर:
f(4)-4f(3)+6f(2)-4f(1)+f(0)=0
$\Rightarrow$ f(4)-4×12+6×8-4×6-3=0
$\Rightarrow$ f(4)-48+48-24-3=0
$\Rightarrow$ f(4)-27=0
$\Rightarrow$ f(4)=27
(1) में x=1 रखने पर:
f(5)-4f(4)+6f(3)-4f(2)+f(1)=0
$\Rightarrow$ f(5)-4×27+6×12-4×8+6=0
$\Rightarrow$ f(5)-108+72-32+6=0
$\Rightarrow$ f(5)-62=0
$\Rightarrow$ f(5)=62
(1) में x=2 रखने पर:
f(6)-4f(5)+6f(4)-4f(3)+f(2)=0
$\Rightarrow$ f(6)-4×62+6×27-4×12=0+8
$\Rightarrow$ f(6)-248+162-48+8=0
$\Rightarrow$ f(6)-126=0
$\Rightarrow$ f(6)=126
Illustration:11. निम्न सारणी में अज्ञात राशि ज्ञात कीजिए।
(Find the missing term in the following tables):
Illustration:11(i).
क्या यह 27 से भिन्न है? यदि है तो क्यों
(Is it different from 27? If yes,why?):
Solution:चूँकि y के चार मान दिए गए हैं अतः तीसरा अन्तर अचर तथा चौथा अन्तर शून्य होना चाहिए।

$\therefore \Delta^4 y_x=0 \\ \Rightarrow(E-1)^4 y_x=0 \\ \Rightarrow\left(E^4-4 E^3+6 E^2-4 E+1\right) y_x=0 \\ \Rightarrow E^4 y_x-4 E^3 y_x+6 E^2 y_x-4 E y_x+y_x=0 \\ \Rightarrow y_{x+4}-4 y_{x+3}+6 y_{x+2}-4 y_{x+1}+y_x=0$
x=0 रखने पर:

$\Rightarrow y_4-4 y_3+6 y_2-4 y_1+y_0=0 \\ \Rightarrow 81-4 y_3+6 \times 9-4 \times 3+1=0 \\ \Rightarrow 81-4 y_3+54-12+1=0 \\ \Rightarrow-4 y_3+124=0 \\ \Rightarrow y_3=\frac{124}{4} \\ \Rightarrow y_3=31$
Illustration:11(ii).
Solution:चूँकि y के पाँच मान दिए गए हैं अतः चौथा अन्तर अचर तथा पाँचवा अन्तर शून्य होना चाहिए।

$\therefore \Delta^5 y_x=0 \\ (E-1)^5 y_x=0 \\ \left(E^5-5 E^4+10 E^3-10 E^2+5 E-1\right) y x=0 \\ \Rightarrow y_{x+5 \times .1}-5 y_{x+4 \times .1}+10 y_{x+3 \times .1}-10 y_{x+2 \times .1} +5 y_{x+1 \times .1}-y_x=0 \cdots(1) \\ \text { put } x=2 \\ \Rightarrow y_{2.5}-5 y_{2.4}+10 y_{2.3}-10 y_{2.2}+5 y_{2.1}-y_2=0 \\ \Rightarrow 0.082-5 \times y_{5+10 \times 0.100}-10 \times 0.111+5 y_2-0.135=0 \\ \Rightarrow 0.082-5 y_5+1-1.11+5 y_2-0.135=0 \\ \Rightarrow 5 y_2-5 y_5-0.163=0 \\ \Rightarrow 5 y_2-5 y_5=0.163 \cdots(2) \\ \text{put } x=2.1 \text{ in (1)} \\ y_{2.6}-5 y_{2.5}+10 y_{2.4}-10 y_{2.3}+5 y_{2.2}-y_{2.1}=0 \\ \Rightarrow 0.074-5 \times 0.082+10 y_5-10 \times 0.100+5 \times 0.111-y_2=0 \\ \Rightarrow 0.074-0.41+10 y_5-1+0.555-y_2=0 \\ \Rightarrow-y_2+10 y_5-0.781=0 \\ \Rightarrow-y_2+10 y_5=0.781 \ldots(3)$
समीकरण (3) को 5 से गुणा करने पर:

$\begin{array}{ll}-5 y_2+50 y_5=3.905 \cdots(4)\\ 5 y_2-5 y_5=0.163 \cdots(2) \\ \text{ जोड़ने पर: } \\ \hline \end{array} \\ 45 y_5=4.068 \\ \Rightarrow y_5=\frac{4.068}{45}=0.0904 \\ \Rightarrow y_5 \approx 0.090 \\ y_5$ का मान समीकरण (3) में रखने पर:

$-y_2+10 \times 0.090=0.781 \\ -y_2=0.781-0.9 \\ \Rightarrow y_2=0.119, y_5=0.90$
उपर्युक्त उदाहरणों के द्वारा अन्तर संकारकों के सम्बन्ध (Relations of Difference Operators),परिमित अन्तर कलन (Calculus of Finite Differences) को समझ सकते हैं।

3.अन्तर संकारकों के सम्बन्ध पर आधारित समस्याएँ (Problems Based on Relations of Difference Operators):

Relations of Difference Operators

(1.)निम्न सारणी में अज्ञात राशि ज्ञात कीजिए
(Obtain the estimate of the missing figures in the following table):

(2.)सिद्ध करो कि (prove that): $f(4)=f(3)+\Delta f(2)+\Delta^2 f(1)+\Delta^3 f(1)$
उत्तर (Answer):(1.)f(3)=27,f(5)=125
उपर्युक्त सवालों को हल करने पर अन्तर संकारकों के सम्बन्ध (Relations of Difference Operators),परिमित अन्तर कलन (Calculus of Finite Differences) को ठीक से समझ सकते हैं।

Also Read This Article:- Numerical Integration by Simpson Rule

4.अन्तर संकारकों के सम्बन्ध (Frequently Asked Questions Related to Relations of Difference Operators),परिमित अन्तर कलन (Calculus of Finite Differences) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:

अन्तर संकारकों के सम्बन्ध (Relations of Difference Operators) तथा परिमित
अन्तर कलन पर आधारित सवालों को हल करके समझने का प्रयास करेंगे।