Regression Lines in Statistics

Mathematics Satyam June 24, 2023 Statistics No Comments

Contents hide

1 1.सांख्यिकी में प्रतीपगमन रेखाएँ (Regression Lines in Statistics),सांख्यिकी में प्रतीपगमन गुणांक (Regression Coefficient in Statistics):

1.1 2.सांख्यिकी में प्रतीपगमन रेखाएँ के उदाहरण (Regression Lines in Statistics Examples):

1.2 3.सांख्यिकी में प्रतीपगमन रेखाएँ की समस्याएँ (Regression Lines in Statistics Problems):

1.2.1 4.सांख्यिकी में प्रतीपगमन रेखाएँ (Frequently Asked Questions Related to Regression Lines in Statistics),सांख्यिकी में प्रतीपगमन गुणांक (Regression Coefficient in Statistics) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:

1.2.2 प्रश्न:1.सरल एवं बहुगुणी प्रतीपगमन में क्या अन्तर है? (What is the Difference Between Simple and Multiple Regression?):

1.2.3 प्रश्न:2.प्रतीपगमन रेखाएँ दो क्यों होती हैं (Why are There Two Regression Lines?):

1.2.4 प्रश्न:3.किन परिस्थितियों में केवल एक ही प्रतीपगमन रेखा हो सकती है? (Under What Conditions Can There be Only One Regression Line?):

1.2.4.1 Regression Lines in Statistics

2 सांख्यिकी में प्रतीपगमन रेखाएँ (Regression Lines in Statistics)

2.1 Regression Lines in Statistics

1.सांख्यिकी में प्रतीपगमन रेखाएँ (Regression Lines in Statistics),सांख्यिकी में प्रतीपगमन गुणांक (Regression Coefficient in Statistics):

Regression Lines in Statistics

सांख्यिकी में प्रतीपगमन रेखाएँ (Regression Lines in Statistics),दो समंक श्रेणियों के विभिन्न मूल्यों के पारस्परिक औसत संबंध (Average Relationship) को व्यक्त करने वाली सर्वोपयुक्त रेखाओं (Lines of the best fit) को प्रतीपगमन रेखाओं (Regression Lines) के नाम से जाना जाता है।ये रेखाएं एक समंक श्रेणी के औसत मूल्यों से संबंधित दूसरी श्रेणी के सर्वोत्तम औसत मूल्यों (Mean Values) को व्यक्त करती हैं।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:-Regression Coefficient in Statistics

2.सांख्यिकी में प्रतीपगमन रेखाएँ के उदाहरण (Regression Lines in Statistics Examples):

Example:6.निम्नलिखित प्रस्तुत सूचनाओं से कार्ल पियर्सन का सहसम्बन्ध गुणांक तथा प्रतीपगमन की दोनों समीकरणों की परिगणना कीजिएः
(Calculate Karl Pearson’s coefficient of correlation and both regression equations from the following given information):

$\begin{array}{|p{3cm}|c|c|c|c|c|c|c|c|c|c|} \hline Age of husband & 18 & 19 & 20 & 21 & 22 & 23 & 24 & 25 & 26 & 27 \\ \hline Age of Wives & 17 & 17 & 18 & 18 & 18 & 19 & 19 & 20 & 21 & 21 \\ \hline \end{array}$
Solution:Calculation of Regression Equations

$\begin{array}{|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|} \hline \text{S.N.} & Age of Husbands & Deviations from A=23 & Deviations square & Age of Wives & Deviations from A=19 & Deviations square & product of deviation\\ \hline & X & dx & d^{2}x & Y & dy & d^{2}y & dxdy \\ \hline 1 & 18 & -5 & 25 & 17 & -2 & 4 & 10 \\ \hline 2 & 19 & -4 & 16 & 17 & -2 & 4 & 8 \\ \hline 3 & 20 & -3 & 9 & 18 & -1 & 1 & 3\\ \hline 4 & 21 & -2 & 4 & 18 & -1 & 1 & 2\\ \hline 5 & 22 & -1 & 1 & 18 & -1 & 1 &1 \\ \hline 6 & 23 & 0 & 0 & 19 & 0 & 0 & 0\\ \hline 7 & 24 & 1 & 1 & 19 & 0 & 0 & 0\\ \hline 8 & 25 & 2 & 4 & 20 & 1 & 1 &2\\ \hline 9 & 26 & 3 & 9 & 21 & 2 & 4 & 6 \\ \hline 10 & 27 & 4 & 16 & 21 & 2 & 4 & 8 \\ \hline Total & 225 & -5 & 85 & 188 & -2 & 20 & 40\\ \hline N=10 & \Sigma X & \Sigma dx & \Sigma d^{2}x & \Sigma Y & \Sigma dy & \Sigma d^{2}y & \Sigma dxdy\\ \hline\end{array}$
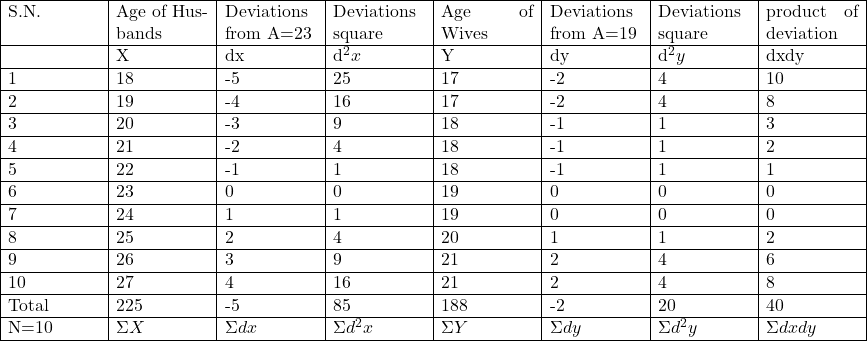
प्रतीपगमन गुणांक (Regression Coefficient)
X का Y पर (X on Y):

$b_{x y} =\frac{N \Sigma d x d y-(\Sigma d x)(\Sigma d y)}{N \Sigma d^2 y-(\Sigma d y)^2} \\ =\frac{10 \times 40-(-5) \times (-2)}{10 \times 20-(-2)^2} \\ =\frac{400-10}{200-4}=\frac{390}{196}=1.989795 \\ b_{xy} \approx 1.9898$
Y का X पर (Y on X):

$b_{yx}=\frac{N \Sigma d x d y-(\Sigma d x)(\Sigma d y)}{N \Sigma d^2 x-(\Sigma d x)^2} \\ =\frac{10 \times 40-(-5) \times (-2)}{10 \times 85-(-5)^2}=\frac{400-40}{850-25} \\ =\frac{390}{825}=0.47272 \\ b_{yx} \approx 0.4727$
समान्तर माध्य (Arithmetic Mean)

$\overline{X}=\frac{\Sigma X}{N} \\ =\frac{225}{10} \\ =22+0.5 \\ \Rightarrow \overline{X}=22.5 \\ \overline{Y}=\frac{\Sigma Y}{N} \\ =\frac{188}{10}=18.8 \\ \Rightarrow \overline{Y}=18.8$
प्रतीपगमन समीकरण x का y परः

$(X-\overline{X}) =b_{xy}(Y-\overline{Y}) \\ X-22.5 =1.9998(Y-18.8) \\ \Rightarrow X-22.5 =1.9998 Y-37.59624 \\ \Rightarrow X=1.9998 Y-37.59624+22.5 \\ \Rightarrow X=1.99 Y-15.09$
प्रतीपगमन समीकरण y का x परः

(Y-\overline{Y}) =b_{yx}(X-\overline{X}) \\ Y-18.8 =0.4727(X-22.5) \\ \Rightarrow Y-18.8=0.4727 X-10.63575 \\ \Rightarrow Y=0.4727 X-10.63575+18.8 \\ \Rightarrow Y =0.47 X+8.164

Cofficient of correlation

$r =\sqrt{b_{xy} \times b_{yx}} \\ =\sqrt{1.9898 \times 0.4727}=0.9698 \\ r \approx 0.97$
Example:7.निम्नलिखित समंकों से सहसम्बन्ध गुणांक (r) का परिकलन कीजिए और प्रतीपगमन रेखाएँ ज्ञात कीजिएः
(From the following data,calculate coefficient of correlation and determine the two regression lines):

$\begin{array}{|p{1cm}|c|c|c|c|c|c|c|c|c|c|} \hline X & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\ \hline Y & 9 & 8 & 10 & 12 & 11 & 13 & 14 & 16 & 15 \\ \hline \end{array}$
Y का अनुमान ज्ञात कीजिए जो औसत रूप से X=6.2 का तत्संवादी हो।
(Estimate the value Y corresponding to X=6.2)
Solution:Calculation of Regression Lines

$\begin{array}{|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|} \hline \text{S.N.} & X & Deviations from A=5 & Deviations square & Y & Deviations from A=11 & Deviations square & product of deviation\\ \hline & & dx & d^{2}x & & dy & d^{2}y & dxdy \\ \hline 1 & 1 & -4 & 16 & 9 & -2 & 4 & 8 \\ \hline 2 & 2 & -3 & 9 & 8 & -3 & 9 & 9 \\ \hline 3 & 3 & -2 & 4 & 10 & -1 & 1 & 2\\ \hline 4 & 4 & -1 & 1 & 12 & 1 & 1 & -1\\ \hline 5 & 5 & 0 & 0 & 11 & 0 & 0 &0\\ \hline 6 & 6 & 1 & 1 & 13 & 2 & 4 & 2\\ \hline 7 & 7 & 2 & 4 & 14 & 3 & 9 & 6\\ \hline 8 & 8 & 3 & 9 & 16 & 5 & 25 & 15\\ \hline 9 & 9 &4 & 16 & 15 & 4 & 16 & 16 \\ \hline Total & 45 & 0 & 60 & 108 & 9 & 69 & 57\\ \hline N=10 & \Sigma X & \Sigma dx & \Sigma d^{2}x & \Sigma Y & \Sigma dy & \Sigma d^{2}y & \Sigma dxdy\\ \hline\end{array}$

समान्तर माध्य (Mean)
$\overline{X}=A_{x}+\frac{\Sigma dx}{dy} \\ =5+\frac{0}{10} \\ \overline{X}=5 \\ \overline{X}=A_{x}+\frac{\Sigma dx}{dy} \\ =5+\frac{0}{10} \\ \overline{X}=5$
प्रतीपगमन गुणांक (Regression Coefficient)
X का Y पर (X on Y)
$b_{xy}=\frac{N \cdot \Sigma d x d y-(\Sigma d x)(\Sigma d y)}{N \cdot \Sigma d^2 y-(\Sigma d y)^2} \\ =\frac{9 \times 57-0 \times 9}{9 \times 69-(9)^2} \\ =\frac{513}{621-81}=\frac{513}{540}=0.95 \\ \Rightarrow b_{xy}=0.95$
Y on X:-
$b_{yx}=\frac{N \Sigma d x d y-(\Sigma d x)(\Sigma d y)}{N \cdot \Sigma d^2 x-(\Sigma d x)^2} \\ =\frac{9 \times 57-0 \times 9}{9 \times 60-(0)^2}=\frac{513}{540} \\ \Rightarrow b_{yx}=0.95$
X का Y पर प्रतीपगमन समीकरण
$(X-\overline{X})=b_{xy}(Y-\overline{Y}) \\ \Rightarrow(X-5)=+0.95(Y-12) \\ \Rightarrow X-5=0.95 Y-11.4 \\ \Rightarrow X=0.95 Y-11.4+5 \\ \Rightarrow X=0.95 Y-6.4$
Y का X पर प्रतीपगमन समीकरण
$Y-\overline{Y}=b_{yx}(X-\overline{X}) \\ \Rightarrow Y-12=0.95(X-5) \\ \Rightarrow Y=0.95 X-4.75+12 \\ \Rightarrow Y=0.95 X+7.25$
जब X=6.2
$Y_{6.2}=0.95 \times 6.2+7.25 \\ =5.89+7.25 \\ \Rightarrow Y_{6.2}=13.14 \\ r=\sqrt{b_{xy} \times b_{yx}}=\sqrt{0.95 \times 0.95} \\ \Rightarrow r=+ 0.95$
Example:8.निम्न आंकड़ों से प्रतीपगमन समीकरण ज्ञात कीजिएः
(Determine the two regression equations from the following data):

$\begin{array}{|p{1cm}|c|c|c|c|c|c|c|c|c|c|} \hline X & 1 & 3 & 4 & 6 & 8 & 9 & 11 & 14 \\ \hline Y & 1 & 2 & 4 & 4 & 5 & 6 & 8 & 9 \\ \hline \end{array}$
Solution:Calculation of Regression Lines

$\begin{array}{|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|} \hline \text{S.N.} & X & Deviations from A=8 & Deviations square & Y & Deviations from A=5 & Deviations square & product of deviation \\ \hline & & dx & d^{2}x & & dy & d^{2}y & dxdy \\ \hline 1 & 1 & -7 & 49 & 1 & -4 & 16 & 28 \\ \hline 2 & 3 & -5 & 25 & 2 & -3 & 9 & +15 \\ \hline 3 & 4 & -4 & 16 & 4 & -1 & 1 & 4 \\ \hline 4 & 6 & -2 & 4 & 4 & -1 & 1 & 2 \\ \hline 5 & 8 & 0 & 0 & 5 & 0 & 0 & 0 \\ \hline 6 & 9 & 1 & 1 & 6 & 1 & 1 & 1\\ \hline 7 & 11 & 3 & 9 & 8 & 3 & 9 & 9 \\ \hline 8 & 14 & 6 & 36 & 9 & 4 & 16 & 24 \\ \hline Total & 56 & -8 & 140 & 39 & -1 & 53 & 83\\ \hline N=10 & \Sigma X & \Sigma dx & \Sigma d^{2}x & \Sigma Y & \Sigma dy & \Sigma d^{2}y & \Sigma dxdy \\ \hline\end{array}$

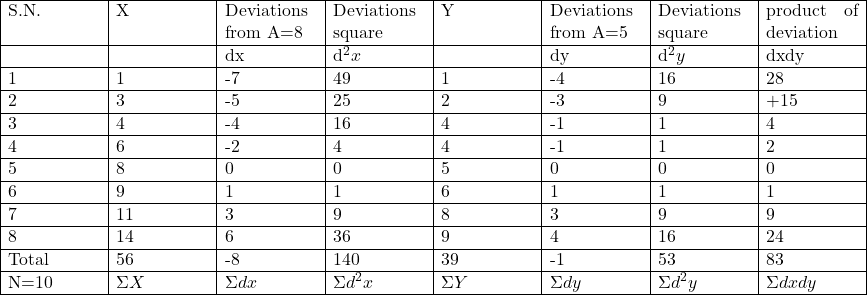
Mean values of series X and Y
$\overline{X}=\frac{\Sigma X}{N}=\frac{56}{8}=7 \\ \overline{Y}=\frac{39}{8}=4.875$
Regression coefficent X on Y
$b_{xy}=\frac{N \cdot \Sigma d x d y-(\Sigma d x)(\Sigma d y)}{N \cdot \Sigma d^2 y-(\Sigma d y)^2}=\frac{8 \times 83-(-8)(-1)}{8 \times 53-(-1)^2} \\ =\frac{664-8}{424-1}=\frac{656}{423}=1.5508 \\ \Rightarrow b_{xy} \approx 1.55$
Regression coefficent Y on X
$b_{yx}=\frac{N \Sigma d x d y-(\Sigma d x)(\Sigma d y)}{N \cdot \Sigma d^2 x-(\Sigma d x)^2}=\frac{8 \times 83-(-8)(-1)}{8 \times 140-(-8)^2}=\frac{664-8}{1120-64} \\=\frac{656}{1056}=0.6212 \\ \Rightarrow b_{yx} \approx 0.62$
Regression Equation: X on Y
$X-\overline{X}=b_{xy}(Y-\overline{Y}) \\ X-7=1.55(Y-4.875) \\ \Rightarrow X=1.55 Y-7.55625+7 \\ \Rightarrow X=1.55 Y-0.55$
Regression Equation: Y on X

Y-\overline{Y}=b_{yx}(X-\overline{X}) \\ Y-4.875=0.62(X-7) \\ =0.62 X-4.34+4.875 \\ \Rightarrow Y=0.62 X+0.53

Regression Lines in Statistics

Example:9.सात नगरों में मारूती कार की माँग के सम्बन्ध में किए गए सर्वेक्षण से निम्न समंक प्राप्त हुए हैंः
(An investigation with the demand for Maruti car in 7 towns has resulted in the following data):

$\begin{array}{|p{3cm}|c|c|c|c|c|c|c|c|c|c|} \hline Population (000's) X & 11 & 14 & 14 & 17 & 17 & 21 & 25 \\ \hline No. of cors & 15 & 27 & 27 & 30 & 34 & 38 & 46 \\ \hline \end{array}$
Y का X पर सरल रेखीय प्रतीपगमन समीकरण ज्ञात कीजिए तथा एक नगर में कारों की मांग का अनुमान लगाइए जिसकी जनसंख्या 30 हजार हो।
(Fit a linear regression of Y on X and estimate the demand of cars for a town with a population of 30 thousand.)
Solution:Calculation of Regression Line

$\begin{array}{|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|} \hline \text{S.N.} & X & Deviations from A=17 & Deviations square & Y & Deviations from A=30 & Deviations square & product of deviation \\ \hline & (000's) & dx & d^{2}x & & dy & d^{2}y & dxdy \\ \hline 1 & 11 & -6 & 36 & 15 & -15 & 225 & 90 \\ \hline 2 & 14 & -3 & 9 & 27 & -3 & 9 & 9 \\ \hline 3 & 14 & -3 & 9 & 27 & -3 & 9 & 9 \\ \hline 4 & 17 & 0 & 0 & 30 & 0 & 0 & 0 \\ \hline 5 & 17 & 0 & 0 & 34 & 4 & 16 & 0 \\ \hline 6 & 21 & 4 & 16 & 38 & 8 & 64 & 32 \\ \hline 7 & 25 & 8 & 64 & 46 & 16 & 256 & 128 \\ \hline Total & 119 & 0 & 134 & 217 & 7 & 579 & 268 \\ \hline N=10 & \Sigma X & \Sigma dx & \Sigma d^{2}x & \Sigma Y & \Sigma dy & \Sigma d^{2}y & \Sigma dxdy\\ \hline\end{array}$

Mean Values of series X and Y
$\overline{X}=\frac{\Sigma X}{N}=\frac{119}{7}=17 \\ \overline{Y}=\frac{\Sigma Y}{N}=\frac{217}{7}=31$
Regression coefficient Y on X
$b_{yx}=\frac{N \Sigma d x d y-(\Sigma d x)(\Sigma d y)}{N \cdot \Sigma d^2 x-(\Sigma d x)^2}= \frac{7 \times 268-(0)(7)}{7 \times 13 y-(0)^2} =\frac{1876}{938}=2$
Regression Equation : Y on X
$Y-\overline{Y}=b_{yx}(X-\overline{X}) \\ \Rightarrow Y-31 =2(X-17) \\ \Rightarrow Y=2X-34+31 \\ \Rightarrow Y =2X-3$
जब X=30
$Y_{30} =2 \times 30-3 \\ =60-3 \\ Y_{30} =57$
Example:10.निम्न समंकों से X पर Y एवं Y पर X के प्रतीपगमन गुणांकों को ज्ञात करिए एवं सहसम्बन्ध गुणांक भी ज्ञात करो।
(Find the regression coefficient of Y on X and X on Y for the following data and also find value of r=?)

$\begin{array}{|p{1cm}|c|c|c|c|c|c|c|c|c|c|} \hline X & 3 & 2 & -1 & 6 & 4 & -2 & 5 \\ \hline Y & 5 & 13 & 12 & -1 & 2 & 20 & 0 \\ \hline \end{array}$
Solution:Calculation of Regression Coefficient

$\begin{array}{|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|} \hline \text{S.N.} & deviations & square of deviation & deviations & square of deviation & product of deviations \\ \hline & dx & d^{2}x & & d^{2}y & dxdy \\ \hline 1 & 3 & 9 & 5 & 25 & 15 \\ \hline 2 & 2 & 4 & 13 & 169 & 26 \\ \hline 3 & -1 & 1 & 12 & 144 & -12 \\ \hline 4 & 6 & 36 & -1 & 1 & -6 \\ \hline 5 & 4 & 16 & 2 & 4 & 8 \\ \hline 6 & -2 & 4 & 20 & 400 & -40 \\ \hline 7 & 5 & 25 & 0 & 0 & 0 \\ \hline Total N=7 & 17 & 95 & 51 & 743 & -9 \\ \hline & \Sigma dx & \Sigma d^{2}x & \Sigma dy & \Sigma d^{2}y & \Sigma dxdy\\ \hline \end{array}$

प्रतीपगमन गुणांक (Regression Coefficient)
X का Y पर (X on Y):
$b_{xy}=\frac{N \Sigma dx dy-(\Sigma d x)(\Sigma d y)}{N \Sigma d^2 y-(\Sigma d y)^2} \\ =\frac{7 \times-9-17 \times 51}{7 \times 743-(51)^2} \\ =\frac{-63-867}{5201-2601} \\ =-\frac{930}{2600}=-0.35769 \\ b_{xy} \approx-0.358$
Y का X पर (Y on X):
$b_{yx} =\frac{N \Sigma d x d y-(\Sigma d x)(\Sigma d y)}{N \Sigma d^2 y-(\Sigma d x)^2} \\ =\frac{7 \times-9-17 \times 51}{7 \times 95-(17)^2} \\ =\frac{-63-867}{665-289} \\ =\frac{-930}{376}=-2.4734 \\ b_{yx} \approx-2.473$
coefficient of correlation:
$r=\sqrt{b_{xy} \times b_{yx}} \\ =-\sqrt{(-0.358 \times-2.473)} \\ =-0.9409 \\ r \approx-0.94$

Example:11.निम्न दो चर मूल्यों से प्रतीपगमन समीकरण बनाइए और उन चर-मूल्यों में सहसम्बन्ध भी ज्ञात कीजिएः
(From the two series given below calculate two equations of regression, viz X on Y and Y on X and find the coefficient of correlation):

$\begin{array}{|p{1cm}|c|c|c|c|c|c|c|c|c|c|} \hline X & 78 & 89 & 97 & 69 & 59 & 79 & 68 & 57 \\ \hline Y & 125 & 137 & 156 & 112 & 107 & 136 & 123 & 108 \\ \hline \end{array}$
Solution:Calculation of Regression Equations

$\begin{array}{|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|} \hline \text{S.N.} & X & Deviations from A=59 & Deviations square & Y & Deviations from A=107 & Deviations square & product of deviation\\ \hline & & dx & d^{2}x & & dy & d^{2}y & dxdy \\ \hline 1 & 78 & 19 & 361 & 125 & 18 & 324 & 342 \\ \hline 2 & 89 & 30 & 900 & 137 & 30 & 900 & 900 \\ \hline 3 & 97 & 38 & 1444 & 156 & 49 & 2401 & 1862 \\ \hline 4 & 69 & 10 & 100 & 112 & 5 & 25 & 50 \\ \hline 5 & 59 & 0 & 0 & 107 & 0 & 0 & 0\\ \hline 6 & 79 & 20 & 400 & 136 & 29 & 841 & 580 \\ \hline 7 & 68 & 9 & 81 & 123 & 16 & 256 & 144 \\ \hline 8 & 57 & -2 & 4 & 108 & 1 & 1 & -2\\ \hline Total & 596 & 124 & 3290 & 1004 & 148 & 4748 & 3876 \\ \hline N=8 &\Sigma X & \Sigma dx & \Sigma d^{2}x & \Sigma Y & \Sigma dy & \Sigma d^{2}y & \Sigma dxdy \\ \hline\end{array}$

Mean value of series X and Y
$\overline{X}=\frac{\Sigma X}{N}=\frac{596}{8}=74.5 \\ \overline{Y}=\frac{\Sigma Y}{N}=\frac{1004}{8}=125.5$
Regression coefficient X on Y
$b_{xy}=\frac{N \Sigma d x d y-(\Sigma d x)(\Sigma d y)}{N \cdot \Sigma d^2 y-(\Sigma d y)^2} \\ =\frac{8 \times 3876-124 \times 148}{8 \times 4748-(148)^2} \\ =\frac{31008-18352}{37984-21904}=\frac{12656}{16080} \\ =0.78706 \\ b_{xy} \approx+0.787$
Y on X:
$b_{yx}=\frac{N \Sigma dxdy-(\Sigma d x)(\Sigma d y)}{N \cdot \Sigma d^2 x-(\Sigma dx)^2} \\ =\frac{8 \times 3876-(124)(148)}{8 \times 3290-(124)^2} \\ =\frac{31008-18352}{26320-15376} =\frac{12656}{10944} \\ =1.1564 \\ b_{yx}\approx 1.156$
Regresion Equation : X on Y
$X-\overline{X}=b_{xy}(Y-\bar{y}) \\ X-74.5=0.787(Y-125.5) \\ \Rightarrow X=0.787Y-98.7685+74.5 \\ \Rightarrow x=0.787 Y-24.27$
Y on X
$Y-\overline{Y}=b_{yx}(X-\overline{X}) \\ Y-125.5=1.156(X-74.5) \\ \Rightarrow X=1.156 X-86.122+125.5 \\ \Rightarrow X=1.156 X+39.38 \\ r=\sqrt{b_{yx} \times b_{yx}} \\ =\sqrt{(0.787 \times 1.156)}=\sqrt{0.909772}=0.9538 \\ \Rightarrow r \approx 0.954$
उपर्युक्त उदाहरणों के द्वारा सांख्यिकी में प्रतीपगमन रेखाएँ (Regression Lines in Statistics),सांख्यिकी में प्रतीपगमन गुणांक (Regression Coefficient in Statistics) को समझ सकते हैं।

3.सांख्यिकी में प्रतीपगमन रेखाएँ की समस्याएँ (Regression Lines in Statistics Problems):

Regression Lines in Statistics

(1.)गत सात वर्षों के लिए किसी वस्तु की पूर्ति और कीमत के समंक नीचे दिए हुए हैं।कीमत की पूर्ति पर प्रतीपगमन समीकरण ज्ञात कीजिए और उससे 1978 में सम्भावित कीमत अनुमानित कीजिए जबकि पूर्ति 110 होः
(The figures of supply and price of a commodity for the last seven years are given below.obtain equation of regression of price over supply and estimate the most likely price in 1978 when supply in 110):

$\begin{array}{|p{1cm}|c|c|c|c|c|c|c|c|c|c|} \hline Year & 1971 & 1972 & 1973 & 1974 & 1975 & 1976 & 1977 \\ \hline Supply & 80 & 84 & 86 & 88 & 92 & 96 & 97 \\ \hline Price & 12 & 11 & 15 & 15 & 18 & 16 & 18 \\\hline \end{array}$
(2.)निम्नलिखित समंकों से सहसम्बन्ध और समाश्रयण गुणांकों को ज्ञात कीजिए।Y आश्रित चर हैः
(From the following data, calculate correlation coefficient and regression coefficient.Y is the dependent variable):

$\begin{array}{|p{1cm}|c|c|c|c|c|c|c|c|c|c|} \hline X & 1 & 2 & 3 & 4 & 5 \\ \hline Y & 165 & 184 & 142 & 186 & 338 \\ \hline \end{array}$
उत्तर (Answers):(1.)Y=0.3656-17.533 , $Y_{110}=22.68$
(2.)r=+0.71 , $b_{xy}=0.01447, b_{yx}=34.8$
उपर्युक्त सवालों को हल करने पर सांख्यिकी में प्रतीपगमन रेखाएँ (Regression Lines in Statistics),सांख्यिकी में प्रतीपगमन गुणांक (Regression Coefficient in Statistics) को ठीक से समझ सकते हैं।

Also Read This Article:-Regression Analysis in Statistics

4.सांख्यिकी में प्रतीपगमन रेखाएँ (Frequently Asked Questions Related to Regression Lines in Statistics),सांख्यिकी में प्रतीपगमन गुणांक (Regression Coefficient in Statistics) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:

प्रश्न:1.सरल एवं बहुगुणी प्रतीपगमन में क्या अन्तर है? (What is the Difference Between Simple and Multiple Regression?):

उत्तर:दो चर मूल्यों के मध्य रेखीय प्रतीपगमन का अध्ययन सरल रेखीय प्रतीगमन कहलाता है।दो मूल्यों (यथा X एवं Y) में से उस चर को स्वतंत्र माना जाता है जो अनुमान का आधार होता है तथा इसके विपरीत दूसरा चर आश्रित चर माना जाता है जिसका अनुमान लगाना होता है।प्रतीपगमन की इस रीति का प्रयोग दो से अधिक चरों के विश्लेषण में भी किया जा सकता है।तीन या तीन से अधिक चरों के विश्लेषण के लिए प्रयुक्त रेखीय प्रतीपगमन को बहुमुखी रेखीय प्रतीपगमन (Multiple Linear Regression) के नाम से संबोधित किया जाता है।

प्रश्न:2.प्रतीपगमन रेखाएँ दो क्यों होती हैं (Why are There Two Regression Lines?):

उत्तर:प्रथम कारणःदो संबंधित समंक श्रेणियों के लिए दो प्रतीपगमन रेखाएँ होती है।एक रेखा X का Y पर प्रतीपगमन (Regression of X on Y) तथा दूसरी रेखा Y का X पर प्रतीगमन (Regression of Y on X) के लिए होती है।
X का Y पर प्रतीपगमन प्रकट करने वाली रेखा की रचना में Y को स्वतंत्र चर तथा X को आश्रित चर माना जाता है।इस रेखा के आधार पर Y के दिए हुए निश्चित औसत मूल्य (माध्य मूल्य) से संबंधित X का सर्वोत्तम औसत मूल्य अनुमानित किया जा सकता है।Y का X पर प्रतीपगमन व्यक्त करने वाली रेखा की रचना करने में X को स्वतन्त्र चर तथा Y को आश्रित चर माना जाता है।इस रेखा के आधार पर X के दिए हुए निश्चित औसत मूल्य से संबंधित Y का सर्वोत्तम औसत मूल्य अनुमानित किया जा सकता है।प्रतीपगमन रेखाओं को खींचते समय आश्रित श्रेणी (Dependent Series) के मूल्यों को उनके माध्य के अधिक से अधिक निकट रखा जाता है।क्योंकि व्यवहार में X एवं Y दोनों ही चरों के अनुमान की आवश्यकता हो सकती है,अतः दो प्रतीपगमन रेखाओं का होना आवश्यक है एक X चर मूल्य के सर्वोत्तम अनुमान के लिए तथा दूसरी Y चर मूल्य के सर्वोत्तम अनुमान के लिए।
द्वितीय कारणःप्रतीपगमन रेखाएं वे सर्वोपयुक्त रेखाएं होती है जिनकी रचना न्यूनतम वर्ग रीति (Least Square Method) की मान्यताओं पर की जाती है।न्यूनतम वर्ग रीति के अनुसार खींची जाने वाली रेखाएं ऐसी होनी चाहिए जिससे विभिन्न बिंदुओं के विचलनों के वर्गों का योग न्यूनतम हो।विभिन्न वास्तविक मूल्यों के बिंदुओं से प्रतीपगमन रेखा तक के विचलनों का माप दो प्रकार से किया जा सकता हैः(अ)क्षैतिज रूप से (Horizontally) अर्थात् भुजाक्ष के समांतर (Parallel to X-axis) तथा (ब)लम्बवत् (Vertically) अर्थात् कोटि अक्ष के समांतर (Parallel to Y-axis)।अतः दोनों विचलनों के पृथक-पृथक योग को न्यूनतम करने के लिए दो प्रतीपगमन रेखाओं का होना आवश्यक है।Y की X पर प्रतीपगमन रेखा इस प्रकार खींची जाती है कि वास्तविक मूल्यों के विभिन्न बिन्दुओं से प्रतीपगमन रेखा तक लम्बवत् विचलनों (Vertical Deviations) के वर्गों का योग न्यूनतम हो जाए।इसी प्रकार X की Y पर प्रतीपगमन रेखा इस प्रकार बनाई जाती है कि वास्तविक मूल्यों के विभिन्न बिंदुओं से प्रतीपगमन रेखा तक के क्षैतिज विचलनों (Horizontal Deviations) के वर्गों का योग न्यूनतम हो जाए।अतः न्यूनतम वर्ग रीति की मान्यताओं के आधार पर भी दो प्रतीपगमन रेखाओं का होना अनिवार्य है।

प्रश्न:3.किन परिस्थितियों में केवल एक ही प्रतीपगमन रेखा हो सकती है? (Under What Conditions Can There be Only One Regression Line?):

उत्तरःजब समंक श्रेणियों में पूर्ण-सहसम्बन्ध (Perfect Correlation) होता है तब X की Y पर तथा Y की X पर एक ही प्रतीपगमन रेखा होती है क्योंकि X एवं Y के पदयुग्मों के आधार पर प्रांकित सभी बिंदु एक ही रेखा के रूप में होते हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा सांख्यिकी में प्रतीपगमन रेखाएँ (Regression Lines in Statistics),सांख्यिकी में प्रतीपगमन गुणांक (Regression Coefficient in Statistics) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Instagram	click here
4.	Linkedin	click here
5.	Facebook Page	click here
6.	Twitter	click here

Regression Lines in Statistics

सांख्यिकी में प्रतीपगमन रेखाएँ
(Regression Lines in Statistics)