Regression Coefficient in Statistics

Mathematics Satyam June 8, 2023 Statistics No Comments

Contents hide

1 1.सांख्यिकी में प्रतीपगमन गुणांक (Regression Coefficient in Statistics),सांख्यिकी में प्रतीपगमन विश्लेषण (Regression Analysis in Statistics):

1.1 2.सांख्यिकी में प्रतीपगमन गुणांक के उदाहरण (Regression Coefficient in Statistics Examples):

1.2 3.सांख्यिकी में प्रतीपगमन गुणांक की समस्याएं (Regression Coefficient in Statistics Problems):

1.2.1 4.सांख्यिकी में प्रतीपगमन गुणांक (Frequently Asked Questions Related to Regression Coefficient in Statistics),सांख्यिकी में प्रतीपगमन विश्लेषण (Regression Analysis in Statistics) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:

1.2.2 प्रश्न:1.प्रतीपगमन रेखाओं की उपयोगिता का वर्णन कीजिए। (Describe the Utility of Regression Lines):

1.2.3 प्रश्न:2.प्रतीपगमन और सहसम्बन्ध में अन्तर समझाइए। (Explain the Difference Between Regression and Correlation):

1.2.4 प्रश्न:3.रेखीय प्रतीपगमन तथा वक्र रेखीय प्रतीपगमन में अन्तर बताइए। (State the Difference Between Linear and Curvilinear Regression):

1.2.4.1 Regression Coefficient in Statistics

2 सांख्यिकी में प्रतीपगमन गुणांक (Regression Coefficient in Statistics)

2.1 Regression Coefficient in Statistics

1.सांख्यिकी में प्रतीपगमन गुणांक (Regression Coefficient in Statistics),सांख्यिकी में प्रतीपगमन विश्लेषण (Regression Analysis in Statistics):

Regression Coefficient in Statistics

सांख्यिकी में प्रतीपगमन गुणांक (Regression Coefficient in Statistics) दो सम्बद्ध श्रेणियों X एवं Y पर प्रतीपगमन विश्लेषण करते समय उनके दो प्रतीपगमन गुणांक (Regression Coefficient) (एक X पर Y का तथा दूसरा Y पर X का) ज्ञात किये जाते हैं।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:-Regression Analysis in Statistics

2.सांख्यिकी में प्रतीपगमन गुणांक के उदाहरण (Regression Coefficient in Statistics Examples):

Example:6.निम्नलिखित प्रस्तुत सूचनाओं से कार्ल पियर्सन का सहसम्बन्ध गुणांक तथा प्रतीपगमन की दोनों समीकरणों की परिगणना कीजिएः
(Calculate Karl Pearsons coefficient of correlation and both regression equations from the following given information):

$\begin{array}{|p{3cm}|c|c|c|c|c|c|c|c|c|c|} \hline Age of husband & 18 & 19 & 20 & 21 & 22 & 23 & 24 & 25 & 26 & 27 \\ \hline Age of Wives & 17 & 17 & 18 & 18 & 18 & 19 & 19 & 20 & 21 & 21 \\ \hline \end{array}$
Solution:Calculation of Regresion coefficient

$\begin{array}{|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|} \hline \text{S.N.} & Age of Husbands & Deviations from A=22 & Deviations square & Age of Wives & Deviations from A=18 & Deviations square & product of deviation\\ \hline & X & dx & d^{2}x & Y & dy & d^{2}y & dxdy \\ \hline 1 & 18 & -4 & 16 & 17 & -1 & 1 & 4 \\ \hline 2 & 19 & -3 & 9 & 17 & -1 & 1 & 3 \\ \hline 3 & 20 & -2 & 4 & 18 & 0 & 0 & 0\\ \hline 4 & 21 & -1 & 1 & 18 & 0 & 0 & 0\\ \hline 5 & 22 & 0 & 0 & 18 & 0 & 0 &0\\ \hline 6 & 23 & 1 & 1 & 19 & 1 & 1 & 1\\ \hline 7 & 24 & 2 & 4 & 19 & 1 & 1 & 2\\ \hline 8 & 25 & 3 & 9 & 20 & 2 & 4 &6\\ \hline 9 & 26 & 4 & 16 & 21 & 3 & 9 & 12 \\ \hline 10 & 27 & 5 & 25 & 21 & 3 & 9 & 15 \\ \hline Total & N=10 & 5 & 85 & & 8 & 26 & 43\\ \hline\end{array}$

प्रतीपगमन गुणांक (Regression Coefficient)

X का Y पर (X on Y)

b_{x y} =\frac{N \Sigma d x d y-(\Sigma d x)(\Sigma d y)}{N \Sigma d^2 y-(\Sigma d y)^2} \\ =\frac{10 \times 43-5 \times 8}{10 \times 26-(8)^2} \\ =\frac{430-40}{260-64}=\frac{390}{196}=1.989795 \\ b_{xy} \approx 1.9898

Y का X पर (Y on X)

$b_{yx}=\frac{N \Sigma d x d y-(\Sigma d x)(\Sigma d y)}{N \Sigma d^2 x-(\Sigma d x)^2} \\ =\frac{10 \times 43-5 \times 8}{10 \times 85-(5)^2}=\frac{430-40}{850-25} \\ =\frac{390}{825}=0.47272 \\ b_{yx} \approx 0.4727$
समान्तर माध्य (Mean)

$\overline{X}=A_x+\frac{\Sigma d x}{N} \\ =22+\frac{5}{10} \\ =22+0.5 \\ \Rightarrow \overline{X}=22.5$
X का Y पर प्रतीपगमन समीकरण

$(X-\overline{X}) =b_{xy}(Y-\overline{Y}) \\ X-22.5 =1.9898(Y-18.8) \\ =1.9898 Y-37.40824 \\ \Rightarrow X=1.9898 Y-37.40824+22.5 \\ \Rightarrow X=1.99 Y-14.9$
समान्तर माध्य (Mean)

$\overline{Y}=A_{y}+\frac{\Sigma d y}{N} \\ =18+\frac{8}{10}=18.8 \\ \Rightarrow \overline{Y}=18.8$
Y का X पर प्रतीपगमन समीकरण (Y on X)

$(Y-\overline{Y}) =b_{yx}(X-\overline{X}) \\ Y-18.8 =0.4727(X-22.5) \\ =0.4727 X-10.63575 \\ \Rightarrow Y=0.4727 X-10.63575+18.8 \\ \Rightarrow Y =0.47 X+8.164 \\ r =\sqrt{b_{xy} \times b_{yx}} \\ =\sqrt{1.9898 \times 0.4727}=0.9698 \\ r \approx 0.97$
Example:7.निम्नलिखित समंकों से सहसम्बन्ध गुणांक (r) का परिकलन कीजिए और प्रतीपगमन रेखाएँ ज्ञात कीजिएः
(From the following data,calculate coefficient of correlation and determine the two regression lines):

$\begin{array}{|p{1cm}|c|c|c|c|c|c|c|c|c|c|} \hline X & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\ \hline Y & 9 & 8 & 10 & 12 & 11 & 13 & 14 & 16 & 15 \\ \hline \end{array}$
Y का अनुमान ज्ञात कीजिए जो औसत रूप से X=6.2 का तत्संवादी हो।
(Estimate the value of Y corresponding to X=6.2)
Solution:Calculation of Regression Coefficient

$\begin{array}{|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|} \hline \text{S.N.} & X & Deviations from A=5 & Deviations square & Y & Deviations from A=11 & Deviations square & product of deviation\\ \hline & & dx & d^{2}x & & dy & d^{2}y & dxdy \\ \hline 1 & 1 & -4 & 16 & 9 & -2 & 4 & 8 \\ \hline 2 & 2 & -3 & 9 & 8 & -3 & 9 & 9 \\ \hline 3 & 3 & -2 & 4 & 10 & -1 & 1 & 2\\ \hline 4 & 4 & -1 & 1 & 12 & 1 & 1 & -1\\ \hline 5 & 5 & 0 & 0 & 11 & 0 & 0 &0\\ \hline 6 & 6 & 1 & 1 & 13 & 2 & 4 & 2\\ \hline 7 & 7 & 2 & 4 & 14 & 3 & 9 & 6\\ \hline 8 & 8 & 3 & 9 & 16 & 5 & 25 & 15\\ \hline 9 & 9 &4 & 16 & 15 & 4 & 16 & 16 \\ \hline Total & N=9 & 0 & 60 & & 9 & 69 & 57\\ \hline\end{array}$
प्रतीपगमन गुणांक (Regression Coefficient)
X का Y पर (X on Y)

$b_{xy}=\frac{N \cdot \Sigma d x d y-(\Sigma d x)(\Sigma d y)}{N \cdot \Sigma d^2 y-(\Sigma d y)^2} \\ =\frac{9 \times 57-0 \times 9}{9 \times 69-(9)^2} \\ =\frac{513}{621-81}=\frac{513}{540}=0.95 \\ \Rightarrow b_{xy}=0.95$
समान्तर माध्य (Mean)

$\overline{X}=A_{x}+\frac{\Sigma dx}{dy} \\ =5+\frac{0}{10} \\ \overline{X}=5$
X का Y पर प्रतीपगमन समीकरण

$(X-\overline{X})=b_{xy}(Y-\overline{Y}) \\ \Rightarrow(X-5)=+0.95(Y-12) \\ \Rightarrow X-5=0.95 Y-11.4 \\ \Rightarrow X=0.95 Y-11.4+5 \\ \Rightarrow X=0.95 Y-6.4$
प्रतीपगमन गुणांक (Regression Coefficient)

$b_{yx}=\frac{N \Sigma d x d y-(\Sigma d x)(\Sigma d y)}{N \cdot \Sigma d^2 x-(\Sigma d x)^2} \\ =\frac{9 \times 57-0 \times 9}{9 \times 60-(0)^2}=\frac{513}{540} \\ \Rightarrow b_{yx}=0.95$
समान्तर माध्य (Mean)

$\overline{Y}=A_{y}+\frac{\Sigma d y}{N}=11+\frac{9}{9}=11+1 \\ \overline{Y}=12$
Y का X पर प्रतीपगमन समीकरण

$Y-\overline{Y}=b_{yx}(X-\overline{X}) \\ \Rightarrow Y-12=0.95(X-5) \\ \Rightarrow Y=0.95 X-4.75+12 \\ \Rightarrow Y=0.95 X+7.25$
जब X=6.2

$Y_{6.2}=0.95 \times 6.2+7.25 \\ =5.89+7.25 \\ \Rightarrow Y_{6.2}=13.14 \\ r=\sqrt{b_{xy} \times b_{yx}}=\sqrt{0.95 \times 0.95} \\ \Rightarrow r=+ 0.95$
Example:8.निम्न आँकड़ों से प्रतीपगमन समीकरण ज्ञात कीजिएः
(Determine the two regression equations from the following data):

$\begin{array}{|p{1cm}|c|c|c|c|c|c|c|c|c|c|} \hline X & 1 & 3 & 4 & 6 & 8 & 9 & 11 & 14 \\ \hline Y & 1 & 2 & 4 & 4 & 5 & 6 & 8 & 9 \\ \hline \end{array}$
Solution:Calculation of Regression Lines

$\begin{array}{|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|} \hline \text{S.N.} & X & \overline{X}=7 & & Y & \overline{Y}=4.875 & d^{2}y & \\ \hline & & dx=X-\overline{X} & d^{2}x & & dy=Y-\overline{Y} & d^{2}y & dxdy \\ \hline 1 & 1 & -6 & 36 & 1 & -3.875 & 15.015625 & 23.25 \\ \hline 2 & 3 & -4 & 16 & 2 & -2.875 & 8.265625 & +11.5 \\ \hline 3 & 4 & -3 & 9 & 4 & -0.875 & 0.765625 & 2.625 \\ \hline 4 & 6 & -1 & 1 & 4 & -0.875 & 0.765625 & 0.875 \\ \hline 5 & 8 & 1 & 1 & 5 & 0.125 & 0.015625 & 0.125 \\ \hline 6 & 9 & 2 & 4 & 6 & 1.125 & 0.015625 & 2.25\\ \hline 7 & 11 & 4 & 16 & 8 & 3.125 & 9.765625 & 12.5\\ \hline 8 & 14 & 7 & 49 & 9 & 4.125 & 17.015625 & 28.875 \\ \hline Total N=8 & 56 & 0 & 132 & 39 & 0 & 51.625 & 82\\ \hline\end{array}$
प्रत्यक्ष रीति (Direct Method)
Mean values of series X and Y

\overline{X}=\frac{\Sigma X}{N}=\frac{56}{8}=7 \\ \overline{Y}=\frac{39}{8}=4.875

Regression coefficent X on Y

b_{xy}=\frac{\Sigma dx dy}{\Sigma d^2 y}=\frac{82}{51.625}=1.58837 \\ \Rightarrow b_{xy} \approx 1.5884

Regression Equation: X on Y

X-\overline{X}=b_{xy}(Y-\overline{Y}) \\ X-7=1.5884(Y-4.875) \\ \Rightarrow X=1.5884 Y-7.74345+7 \\ \Rightarrow X=1.59 Y-0.74

Regression coefficent Y on X
$b_{yx}=\frac{\Sigma dx dy}{\Sigma d^2 x}=\frac{82}{132}=0.62121 \\ \Rightarrow b_{yx} \approx 0.6212$

Regression Equation: Y on X
$Y-\overline{Y}=b_{yx}(X-\overline{X}) \\ Y-4.875=0.6212(X-7) \\ =0.6212 X-4.3484 \\ \Rightarrow Y=0.6212 X-4.3484+4.875 \\ \Rightarrow Y=0.62 X+0.52$
Example:9.सात नगरों में मारुति कार की माँग के सम्बन्ध में किए गए सर्वेक्षण से निम्न समंक प्राप्त हुए हैंः
(An investigation with the demand for Maruti car in 7 towns has resulted in the following data):

$\begin{array}{|p{3cm}|c|c|c|c|c|c|c|c|c|c|} \hline Population (000's) X & 11 & 14 & 14 & 17 & 17 & 21 & 25 \\ \hline No. of cors & 15 & 27 & 27 & 30 & 34 & 38 & 46 \\ \hline \end{array}$
Y का X पर सरल रेखीय प्रतीपगमन ज्ञात कीजिए तथा एक नगर में कारों की माँग का अनुमान लगाइए जिसकी जनसंख्या 30 हजार हो।
(Fit a linear regression of Y on X and estimate the demand of cars for a town with a population of 30 thousand.)
Solution:Calculation of Regression Line

$\begin{array}{|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|} \hline \text{S.N.} & X & \overline{X}=17 & & Y & \overline{Y}=31 & & \\ \hline & (000's) & dx=X-\overline{X} & d^{2}x & & dy=Y-\overline{Y} & d^{2}y & dxdy \\ \hline 1 & 11 & -6 & 36 & 15 & -16 & 256 & 96 \\ \hline 2 & 14 & -3 & 9 & 27 & -4 & 16 & 12 \\ \hline 3 & 14 & -3 & 9 & 27 & -4 & 16 & 12 \\ \hline 4 & 17 & 0 & 0 & 30 & -1 & 1 & 0 \\ \hline 5 & 17 & 0 & 0 & 34 & 3 & 9 & 0 \\ \hline 6 & 21 & 4 & 16 & 38 & 7 & 49 & 28 \\ \hline 7 & 25 & 8 & 64 & 46 & 15 & 225 & 120 \\ \hline Total N=7 & 119 & 0 & 134 & 217 & 0 & 572 & 268 \\ \hline\end{array}$

Mean Values of series X and Y
$\overline{X}=\frac{\Sigma X}{N}=\frac{119}{7}=17 \\ \overline{Y}=\frac{\Sigma Y}{N}=\frac{217}{7}=31$

Regression coefficient Y on X
$b_{yx}=\frac{\Sigma d x d y}{\Sigma d^2 x}=\frac{268}{134}=2$
Regression Equation : Y on X
$Y-\overline{Y}=b_{yx}(X-\overline{X}) \\ \Rightarrow Y-31 =2(X-17) \\ \Rightarrow Y=2X-34+31 \\ \Rightarrow Y =2X-3$

जब X=30,000

Y_{30} =2 \times 30-3 \\ =60-3 \\ Y_{30} =57

Regression Coefficient in Statistics

Example:10.निम्न समंकों X पर Y तथा Y पर X के प्रतीपगमन गुणांकों को ज्ञात करिए एवं सहसम्बन्ध गुणांक भी ज्ञात करो।
(Find the regression coefficient of Y on X and X on Y for the following data and also find value of r=?)

$\begin{array}{|p{1cm}|c|c|c|c|c|c|c|c|c|c|} \hline X & 3 & 2 & -1 & 6 & 4 & -2 & 5 \\ \hline Y & 5 & 13 & 12 & -1 & 2 & 20 & 0 \\ \hline \end{array}$
Solution:Calculation of Regression Coefficient

$\begin{array}{|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|} \hline \text{S.N.} & deviations & square of deviation & deviations & square of deviation & product of deviations \\ \hline & dx & d^{2}x & & d^{2}y & dxdy \\ \hline 1 & 3 & 9 & 5 & 25 & 15 \\ \hline 2 & 2 & 4 & 13 & 169 & 26 \\ \hline 3 & -1 & 1 & 12 & 144 & -12 \\ \hline 4 & 6 & 36 & -1 & 1 & -6 \\ \hline 5 & 4 & 16 & 2 & 4 & 8 \\ \hline 6 & -2 & 4 & 20 & 400 & -40 \\ \hline 7 & 5 & 25 & 0 & 0 & 0 \\ \hline Total N=7 & 17 & 95 & 51 & 743 & -9 \\ \hline & \Sigma dx & \Sigma d^{2}x & \Sigma dy & \Sigma d^{2}y & \Sigma dxdy\\ \hline \end{array}$
प्रतीपगमन गुणांक (Regression Coefficient)
X का Y पर (X on Y):

$b_{xy}=\frac{N \Sigma dx dy-(\Sigma d x)(\Sigma d y)}{N \Sigma d^2 y-(\Sigma d y)^2} \\ =\frac{7 \times-9-17 \times 51}{7 \times 743-(51)^2} \\ =\frac{-63-867}{5201-2601} \\ =-\frac{930}{2600}=-0.35769 \\ b_{xy} \approx-0.358$
Y का X पर (Y on X):

b_{yx} =\frac{N \Sigma d x d y-(\Sigma d x)(\Sigma d y)}{N \Sigma d^2 y-(\Sigma d x)^2} \\ =\frac{7 \times-9-17 \times 51}{7 \times 95-(17)^2} \\ =\frac{-63-867}{665-289} \\ =\frac{-930}{376}=-2.4734 \\ b_{yx} \approx-2.473

coefficient of correlation:

$r=\sqrt{b_{xy} \times b_{yx}} \\ =-\sqrt{(-0.358 \times-2.473)} \\ =-0.9409 \\ r \approx-0.94$
Example:11.निम्न दो चरों के मूल्यों से प्रतीपगमन समीकरण बनाइए और इन चर-मूल्यों में सहसम्बन्ध भी ज्ञात कीजिए।
(From the two series given below calculate the equations of regression, viz X on Y and Y on X and find out coefficient of correlation):

$\begin{array}{|p{1cm}|c|c|c|c|c|c|c|c|c|c|} \hline X & 78 & 89 & 97 & 69 & 59 & 79 & 68 & 57 \\ \hline Y & 125 & 137 & 156 & 112 & 107 & 136 & 123 & 108 \\ \hline \end{array}$
Solution:Calculation of Regression Lines

$\begin{array}{|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|} \hline \text{S.N.} & X & Deviations from A=69 & Deviations square & Y & Deviations from A=107 & Deviations square & product of deviation\\ \hline & & dx=X-A & d^{2}x & & dy=Y-A & d^{2}y & dxdy \\ \hline 1 & 78 & 9 & 81 & 125 & 18 & 324 & 162 \\ \hline 2 & 89 & 20 & 400 & 137 & 30 & 900 & 600 \\ \hline 3 & 97 & 28 & 784 & 156 & 49 & 2401 & 1372\\ \hline 4 & 69 & 0 & 0 & 112 & 5 & 25 & 0 \\ \hline 5 & 59 & -10 & 100 & 107 & 0 & 0 &0\\ \hline 6 & 79 & +10 & 100 & 136 & 29 & 841 & 290\\ \hline 7 & 68 & -1 & 1 & 123 & 16 & 256 & -16\\ \hline 8 & 57 & -12 & 144 & 108 & 1 & 1 & -12\\ \hline Total N=8 & 596 & 1610 & 1004 & 148 & 1 & 1 & -12 \\ \hline &\Sigma X & \Sigma dx & \Sigma d^{2}x & \Sigma Y & \Sigma dy & \Sigma d^{2}y & \Sigma dxdy \\ \hline\end{array}$

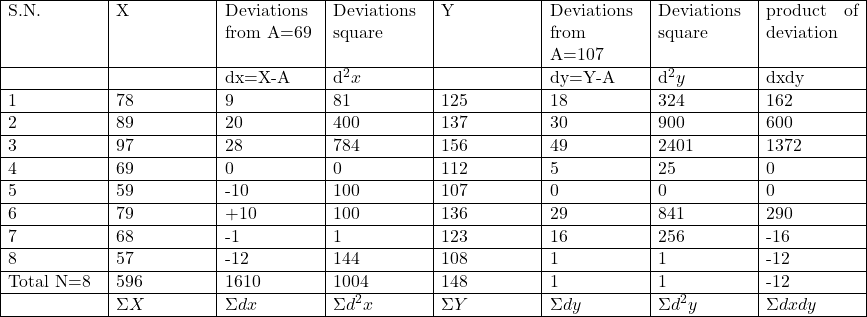
Mean value of series X and Y
$\overline{X}=A+\frac{\Sigma d x}{N}=69+\frac{44}{8}=69+5.5=79.5 \\ \overline{Y}=A+\frac{\Sigma d y}{N}=107+\frac{448}{8}=107+18.5=125.5$

Regression coefficient X on Y
$b_{xy}=\frac{N \Sigma d x d y-(\Sigma d x)(\Sigma d y)}{N \cdot \Sigma d^2 y-(\Sigma d y)^2} \\ =\frac{8 \times 2396-(44)(148)}{8 \times 4748-(148)^2} \\ =\frac{19168-6512}{37984-21904}=\frac{12656}{16080} \\ =0.78706 \\ b_{xy} \approx+0.7871$

Y on X:
$b_{yx}=\frac{N \Sigma dxdy-(\Sigma d x)(\Sigma d y)}{N \cdot \Sigma d^2 x-(\Sigma dx)^2} \\ =\frac{8 \times 2396-(44)(148)}{8 \times 1610-(44)^2} \\ =\frac{19168-6512}{12880-1936} \\=\frac{12656}{10944} \\ =1.15643 \\ b_{yx}\approx 1.1564$

Regresion Equation : X on Y
$X-\overline{X}=b_{xy}(Y-\bar{y}) \\ X-74.5=0.787(Y-125.5) \\ \Rightarrow X=0.787Y-98.7685+74.5 \\ \Rightarrow x=0.787 Y-24.27$
Y on X
$Y-\overline{Y}=b_{yx}(X-\overline{X}) \\ Y-125.5=1.156(X-74.5) \\ \Rightarrow X=1.156 X-86.122+125.5 \\ \Rightarrow X=1.156 X+39.38 \\ r=\sqrt{b_{yx} \times b_{yx}} \\ =\sqrt{(0.787 \times 1.156)}=0.9538 \\ \Rightarrow r \approx 0.954$

Example:12.निम्नलिखित आंकड़ों से प्रतीपगमन समीकरण ज्ञात कीजिएः
(From the following data determine the two regression equations):

$\begin{array}{|p{1cm}|c|c|c|c|c|c|c|c|c|c|} \hline X & 27 & 27 & 27 & 28 & 28 & 28 & 29 & 29 & 30 & 31 \\ \hline Y & 18 & 18 & 19 & 20 & 21 & 21 & 22 & 23 & 24 &25 \\ \hline \end{array}$
Solution:Calculation of Regression Lines

$\begin{array}{|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|p{2cm}|} \hline \text{S.N.} & X & Deviations from A=28 & Deviations square & Y & Deviations from A=21 & Deviations square & product of deviation\\ \hline & & dx & d^{2}x & & dy & d^{2}y & dxdy \\ \hline 1 & 27 & -1 & 1 & 18 & -3 & 9 & 3 \\ \hline 2 & 27 & -1 & 1 & 18 & -3 & 9 & 3 \\ \hline 3 & 27 & -1 & 1 & 19 & -2 & 4 & 2 \\ \hline 4 & 28 & 0 & 0 & 20 & -1 & 1 & 0 \\ \hline 5 & 28 & 0 & 0 & 21 & 0 & 0 &0\\ \hline 6 & 28 & 0 & 0 & 21 & 0 & 0 & 0\\ \hline 7 & 29 & 1 & 1 & 22 & 1 & 1 & 1 \\ \hline 8 & 29 & 1 & 1 & 23 & 2 & 4 & 2 \\ \hline 9 & 30 & 2 & 4 & 24 & 3 & 9 & 6 \\ \hline 10 & 31 & 3 & 9 & 25 & 4 & 16 & 12 \\ \hline Total & N=10 & 4 & 18 & & 1 & 53 & 29 \\ \hline &\Sigma X & \Sigma dx & \Sigma d^{2}x & \Sigma Y & \Sigma dy & \Sigma d^{2}y & \Sigma dxdy \\ \hline\end{array}$

Mean value of Series X and Y
$\overline{X}=A+\frac{\Sigma d x}{N}=28+\frac{4}{10}=28+0.40 \\ \overline{X}=28.40 \\ \overline{Y} =A+\frac{\Sigma d y}{N}=21+\frac{1}{10}=21+0.10 \\ \overline{X}=21.10$

Regression coefficient : X on Y
$b_{xy}=\frac{N \Sigma dx dy-(\Sigma d x)(\Sigma d y)}{N \Sigma d^2 y-(\Sigma d y)^2} \\ =\frac{=10 \times 29-4 \times 1 }{9 \times 53-(1)^2}=\frac{290-4}{530-1} \\=\frac{286}{529} \\ =0.5406 \\ b_{xy} \approx +0.54$
Y on X
$b_{yx}=\frac{N \Sigma d x d y-(\Sigma d x)(\Sigma d y)}{N \Sigma d^2 x-(\Sigma d x)^2} \\ =\frac{10 \times 29-4 \times 1}{10 \times 18-(4)^2}=\frac{290-4}{180-16}=\frac{286}{164} \\ =1.7439 \\ b_{yx} \approx 1.74$
Regression equation: X on Y
$X-\overline{X}=b_{xy}(Y-\overline{Y}) \\ \Rightarrow X-28.4=0.54(Y-21.10) \\ \Rightarrow x=0.54 Y-11.394+28.4 \\ \Rightarrow X=0.54+17.006$
Y on X :
$Y-\overline{Y}=b_{yx}(X-\overline{X}) \\ \Rightarrow Y-21.10=1.74(X-28.4) \\ \Rightarrow Y=1.74 X-49.416+21.10 \\ \Rightarrow Y=1.74 X-28.316$

उपर्युक्त उदाहरणों के द्वारा सांख्यिकी में प्रतीपगमन गुणांक (Regression Coefficient in Statistics),सांख्यिकी में प्रतीपगमन विश्लेषण (Regression Analysis in Statistics) को समझ सकते हैं।

3.सांख्यिकी में प्रतीपगमन गुणांक की समस्याएं (Regression Coefficient in Statistics Problems):

Regression Coefficient in Statistics

(1.)दोनों प्रतीपगमन समीकरण ज्ञात कीजिए तथा प्रतीपगमन गुणांकों की सहायता से सहसम्बन्ध गुणांक निकालिएः
(Find both regression equations and with the help of regression coefficients,calculate the coefficient of correlation):

$\begin{array}{|p{1cm}|c|c|c|c|c|c|c|c|c|c|} \hline X & 17 & 18 & 19 & 19 & 20 & 20 & 21 & 21 & 22 & 23 \\ \hline Y & 12 & 16 & 14 & 11 & 15 & 19 & 22 & 16 & 15 & 20 \\ \hline \end{array}$
(2.)निम्नलिखित मूल्यों से सम्बन्धित समाश्रयण समीकरण निकालिएः
(Determine the regression equations associated with the following values):

$\begin{array}{|p{1cm}|c|c|c|c|c|c|c|c|c|c|} \hline X & 140 & 90 & 130 & 150 & 135 & 150 & 160 & 165 & 158 & 170 \\ \hline Y & 190 & 100 & 170 & 200 & 175 & 190 & 210 & 220 & 205 & 240 \\ \hline \end{array}$
उत्तर (Answers):(1.)X=0.324Y+14.81;Y=1.167X-7.33,r=+0.614
(2.)X=0.607Y+29.47;Y=1.61X-43.13
उपर्युक्त सवालों को हल करने पर सांख्यिकी में प्रतीपगमन गुणांक (Regression Coefficient in Statistics),सांख्यिकी में प्रतीपगमन विश्लेषण (Regression Analysis in Statistics) को ठीक से समझ सकते हैं।

Also Read This Article:-Correlation by Method of Least Squares

4.सांख्यिकी में प्रतीपगमन गुणांक (Frequently Asked Questions Related to Regression Coefficient in Statistics),सांख्यिकी में प्रतीपगमन विश्लेषण (Regression Analysis in Statistics) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:

प्रश्न:1.प्रतीपगमन रेखाओं की उपयोगिता का वर्णन कीजिए। (Describe the Utility of Regression Lines):

उत्तर:व्यावसायिक एवं आर्थिक क्षेत्र में प्रतीपगमन विश्लेषण का अत्यधिक महत्त्व है।प्रबन्धकों द्वारा इस तकनीक का प्रयोग नियन्त्रण उपकरण (Tools for control) के रूप में किया जाता है।इस तकनीक के आधार पर समुचित व्यावसायिक निर्णयन सरल हो जाता है।उदाहरणार्थ,मांग-मूल्य (Demand-price),मांग पूर्ति (Demand-supply),वर्षा की मात्रा व कृषि खाद्यान्नों की उपज,पूंजी की मात्रा में वृद्धि आदि का पूर्वानुमान इस तकनीक के आधार पर संभव होता है।इस आधार पर प्रबंध द्वारा व्यावसायिक उचित निर्णय सरलता से लिए जा सकते हैं।
इसके अतिरिक्त प्रतीपगमन विश्लेषण के आधार पर लिए गए निर्णयों की व्यावहारिकता की कसौटी पर जांच या परीक्षण करना भी संभव होता है।इस तकनीक के आधार पर ज्ञात निष्कर्ष उतने ही अधिक विश्वसनीय होंगे जितना अधिक घनिष्ठ सहसंबंध दो चरों के मध्य होगा।
इस प्रकार इस तकनीक का अध्ययन निम्नलिखित प्रकार से उपयोगी एवं महत्त्वपूर्ण हैः
(1.)पूर्वानुमान (Forecasting):प्रतीपगमन विश्लेषण के आधार पर एक स्वतंत्र मूल्य के लिए आश्रित चर मूल्य का अनुमान लगाया जा सकता है।इसकी सहायता से विभिन्न मूल्यों के लिए मांग का,वर्षा की मात्रा,बीज व खाद के आधार पर खाद्यान्न उपज का,पूँजी की कमी या वृद्धि का लाभों पर प्रभाव का अनुमान लगाया जा सकता है।अतः प्रतीपगमन विश्लेषण द्वारा हम दो चरों के मध्य सहसम्बन्ध की प्रकृति व मात्रा का माप करके पूर्वानुमान की क्षमता प्राप्त करते हैं।
(2.)आर्थिक व व्यावसायिक क्षेत्र में उपयोगिताःइस तकनीक के आधार पर आर्थिक,व्यावसायिक व सामाजिक क्षेत्र में विभिन्न घटनाओं के माध्य सम्बन्धों का विश्लेषण कर उपयोगी निर्णय लिए जा सकते हैं।प्रबन्धकों द्वारा इस तकनीक का प्रयोग नियंत्रण उपकरण के रूप में किया जाता है।
(3.)दो से अधिक चरों में अध्ययन सम्भवःइस तकनीक द्वारा दो से अधिक संबंधित चरों में भी सामान्य माध्य की ओर जाने की प्रवृत्ति का अध्ययन किया जा सकता है।एम.एम. ब्लेयर के शब्दों में, “दो या दो से अधिक चरों के पारस्परिक औसत सम्बन्ध का माप प्रतीपगमन है।”
(4.)सहसम्बन्ध की मात्रा व दिशा का ज्ञान सम्भवःइस तकनीक के आधार पर सहसम्बन्ध की मात्रा तथा दिशा का अनुमान लगाया जा सकता है।

प्रश्न:2.प्रतीपगमन और सहसम्बन्ध में अन्तर समझाइए। (Explain the Difference Between Regression and Correlation):

उत्तर:स्टाॅकटन और क्लार्क ने सहसम्बन्ध एवं प्रतीपगमन में अंतर स्पष्ट करते हुए मत व्यक्त किया है कि ‘ज्ञात एवं अज्ञात के मध्य संबंध के आधार पर अज्ञात चर का अनुमान लगाना प्रतीपगमन विश्लेषण कहलाता है।दो या दो से अधिक चरों के मध्य संबंध की मात्रा (degree) का मापन सहसम्बन्ध विश्लेषण कहलाता है।दो चरों के मध्य सम्बन्ध जितना गहन होगा उतना ही अनुमान पर अधिक विश्वास किया जा सकता है।यह कहा जा सकता है कि सहसंबंध दो चरों के मध्य सम्बन्ध की मात्रा को मापता है,जबकि प्रतीपगमन विश्लेषण यह बताता है कि चर किस प्रकार संबंधित हैं।तारो यामने (Taro Yamane) के मतानुसारः “दो या दो से अधिक कार्य-कारण संबंधों से संबंधित चरों के मध्य संबंध ज्ञात करने के लिए अर्थशास्त्र एवं व्यावसायिक शोध में अत्यधिक प्रयुक्त की जाती है,प्रतीपगमन विश्लेषण कहलाती है।”
सहसम्बन्ध एवं प्रतीपगमन में अन्तर प्रमुख रूप से निम्नवत् हैः
(1.)कारण एवं परिणाम संबंध (Cause and Effect Relationship):सहसंबंध की अपेक्षा प्रतीपगमन विश्लेषण कारण एवं परिणाम संबंध को अधिक स्पष्ट रूप से व्यक्त करता है।दो चरों के मध्य अत्यधिक मात्रा का सहसम्बन्ध होने पर भी यह प्रमाणित रुप से नहीं कहा जा सकता है कि एक कारण है तथा दूसरा परिणाम;लेकिन प्रतीपगमन विश्लेषण में एक चर को स्वतंत्र माना जाता है जिसका मूल्य ज्ञात होता है तथा दूसरा चर-मूल्य आश्रित माना जाता है जिसका अनुमान लगाया जाता है।स्वतंत्र चर कारण तथा आश्रित चर परिणाम होता है।
(2.)संबंध की मात्रा तथा प्रकृति (Degree and Nature of Relationship):सहसम्बन्ध दो या अधिक चरों सहपरिवर्तन की घनिष्ठता की जांच करता है जबकि प्रतीपगमन विश्लेषण इस सह-परिवर्तन की प्रकृति स्पष्ट करता है तथा यह बतलाता है कि एक चर के औसत मूल्य के तत्संवादी दूसरे चर का सम्भाव्य औसत मूल्य क्या होगा? वर्नर हर्श ने इसे स्पष्ट करते हुए अपना मत इस प्रकार व्यक्त किया हैः”जबकि सहसम्बन्ध विश्लेषण दो या अधिक घटनाओं में सहपरिवर्तन की घनिष्ठता की जांच करता है,प्रतीपगमन विश्लेषण इस संबंध की प्रकृति एवं मात्रा का मापन कर हमें भावी अनुमान की क्षमता प्रदान करता है।”

प्रश्न:3.रेखीय प्रतीपगमन तथा वक्र रेखीय प्रतीपगमन में अन्तर बताइए। (State the Difference Between Linear and Curvilinear Regression):

उत्तर:सामान्यतः दो संबंधित श्रेणियों में प्रतीपगमन विश्लेषण करने के लिए बिन्दु रेखीय रीति का प्रयोग किया जाता है।बिन्दुरेखीय रीति के अन्तर्गत X तथा Y चरों को ग्राफ-पत्र पर अंकित कर एक विक्षेप चित्र (scatter diagram) बना लिया जाता है।इस चित्र पर अंकित विभिन्न बिन्दुओं के मध्य से गुजरती हुई दो सर्वोपयुक्त रेखाएँ खींची जाती है।एक रेखा X का Y पर तथा दूसरी Y का X पर सर्वोत्तम अनुमान लगाने हेतु खींची जाती है।ये दो रेखाएँ ही प्रतीपगमन रेखाएँ कहलाती हैं।जब रेखाएँ सरल या सीधी (straight) होती है तो प्रतीपगमन रेखीय (linear) कहलाता है।इस सरल रेखाओं के समीकरण एकघातीय (equations of the first degree) होते हैं।Y की X प्रतीपगमन रेखा का समीकरण Y=a+bX तथा X का Y पर प्रतीपगमन रेखा का समीकरण X=a+bY होता है।यदि बिन्दु रेखा पर खींची जाने वाली ये प्रतीपगमन रेखायें सरलित वक्र (smooth curve) के रूप में होता है तो इन वक्रों द्वारा निर्मित प्रतीपगमन वक्ररेखीय (curvilinear) कहलाता है।
उपर्युक्त प्रश्नों के उत्तर द्वारा सांख्यिकी में प्रतीपगमन गुणांक (Regression Coefficient in Statistics),सांख्यिकी में प्रतीपगमन विश्लेषण (Regression Analysis in Statistics) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Instagram	click here
4.	Linkedin	click here
5.	Facebook Page	click here
6.	Twitter	click here

Regression Coefficient in Statistics

सांख्यिकी में प्रतीपगमन गुणांक
(Regression Coefficient in Statistics)