Regression Analysis in Statistics
1.सांख्यिकी में प्रतीपगमन विश्लेषण (Regression Analysis in Statistics),सांख्यिकी में प्रतीपगमन गुणांक (Regression Coefficient in Statistics):
सांख्यिकी में प्रतीपगमन विश्लेषण (Regression Analysis in Statistics) वह रीति है जिसके माध्यम से एक चर के किसी ज्ञात मूल्य से सम्बन्धित तत्संवादी (corresponding) दूसरे चर का सम्भाव्य मूल्य अनुमानित किया जा सकता है।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Correlation by Method of Least Squares
2.सांख्यिकी में प्रतीपगमन विश्लेषण के उदाहरण (Regression Analysis in Statistics Examples):
अतिलघुत्तरात्मक प्रश्न (Very Short Questions)
Example:1.यदि b_{yx}=0.8, \sigma_x=0.8 व r=0.8 सहसम्बन्ध गुणांक=0.8 हो तो का मान क्या होगा?
(If and r=0.8 find the value of \sigma_y )
Solution: b_{yx}=0.8, \sigma_x=0.8,r=0.8 ,\sigma_y=? \\ \Rightarrow b_{yx}=r \cdot \frac{\sigma_y}{\sigma_x} \\ \Rightarrow 0.8=0.8 \times \frac{\sigma_y}{0.8} \\ \Rightarrow \sigma_y=0.8
Example:2.यदि दोनों प्रतीपगमन गुणांकों के मूल्य -0.5 तथा -1.28 हो तो सहसम्बन्ध गुणांक का मान ज्ञात कीजिए।
(If the value of two regression coefficient are -0.5 and -1.28 ;find the value of coefficient of correlation):
Solution: b_{xy}=-0.5, \quad b_{yx}=-1.28 \\ r=\sqrt{b_{yx} \times b_{xy}} \\ =\sqrt{(-1.28 \times-0.5)} \\ =\sqrt{0.64} \\ \Rightarrow r=0.8
Example:3.यदि x का प्रसरण 9,b_{yx}=0.8 तथा r=0.6 हो तो का मान क्या होगा?
(If variance of x=9,b_{yx}=0.8 and r=0.6,find the value of \sigma_y.)
Solution: \sigma_{x}^2=9 \Rightarrow \sigma_{x}=3, b_{yx}=0.8,r=0.6, \sigma_y=? \\ b_{yx}=r \frac{\sigma_y}{\sigma_x} \\ \Rightarrow 0.8=0.6 \times \frac{\sigma_y}{3} \\ \Rightarrow \sigma_y=\frac{0.8 \times 3}{0.6} \\ \Rightarrow \sigma_y=4
Example:4.X व Y के मध्य सम्बन्ध ज्ञात करने हेतु किए गए सर्वेक्षण के निम्नलिखित परिणाम उपलब्ध हैंः
(The results of a survey conducted for the relationship between x and y are as under):
| Mean | standard Deviation | |
| X | 173 | 63.15 |
| Y | 47.8 | 22.98 |
Coefficient of correlation (r)=+0.57
Y की X पर प्रतीपगमन समीकरण ज्ञात कीजिए
(Compute regression equation of y on x)
Solution: \overline{X}=173, \overline{Y}=47.8,\sigma_x=63.15 \\ \Rightarrow \sigma_{y}=22.98 \quad r=+0.57
Y की X पर प्रतीपगमन समीकरण
(Y-\overline{Y})=r \frac{\sigma_y}{\sigma_x}(X-\overline{X}) \\ \Rightarrow Y-47.8=0.57 \times \frac{22.98}{63.15}(X-\overline{X})\\ \Rightarrow Y-47.8=0.21(X-173) \\ \Rightarrow Y=47.8+0.21 X-36.33 \\ \Rightarrow Y=11.47+0.21 X
Example:5.निम्नलिखित मूल्य प्रस्तुत हैंः
(Given the following values):
r=0.56 , \Sigma dx dy=60 , \sigma_y=4, \Sigma d^2 x=90
(Find the number of items)
पदों की संख्या (N) ज्ञात कीजिए
Solution: \Sigma dx dy=60,\sigma_y=4, \Sigma d^2x=90, r=0.56 \\ r =\frac{\Sigma d x d y}{N \cdot \sigma_x \cdot \sigma y} \\ =\frac{\Sigma d x d y}{N \cdot \sqrt{\frac{d^2 x}{N} } \cdot \sigma_y} \\ \Rightarrow \sqrt{N} =\frac{\Sigma d x d y}{\Sigma \sqrt{d^2 x \sigma_y^{2}}} \\ \Rightarrow N =\frac{(\Sigma dx dy)^2}{r^2 \cdot d^2 x \cdot \sigma_y^2} \\ =\frac{(60)^2}{(0.56)^2 \times 90 \times 4^2} \\ =\frac{3600}{0.3136 \times 90 \times 16} \\ =\frac{3600}{451.584} \\ =7.97 \\ \Rightarrow N=8
Example:6.निम्नलिखित समंकों के आधार पर और r के मान की गणना कीजिएः
(Find the values of and r from the following data:3x=y,4y=3x ,\sigma_x=2
Solution:3x=y,4y=3x
3x=y \Rightarrow x=0.33 y \\ b_{xy}=0.33, \quad 4y=3 x \Rightarrow y=0.75 x \\ b_{yx}=0.75 \\ r=\sqrt{b_{yx} \times b_{xy}}=\sqrt{0.75 \times 0.33} \\ r=+0.4975 \\ b_{xy}=r \frac{\sigma_x}{\sigma_y} \\ 0.33=0.4975 \times \frac{2}{\sigma_y} \\ \sigma_y=\frac{0.4975 \times 2}{0.33} \\ =\frac{0.995}{0.33}=3.015 \\ \Rightarrow \sigma_y=3.015
Example:7.यदि प्रतीपगमन गुणांक 0.8 तथा 0.6 हो तो सहसम्बन्ध गुणांक का मान ज्ञात कीजिएः
(If two regression coefficients are 0.8 and 0.6,find the value of coefficient of correlation):
Solution: b_{xy}=0.8, b_{yx}=0.6 \\ r=\sqrt{b_{xy} \times b_{yx}} \\ =\sqrt{0.8 \times 0.6} \\ =\sqrt{0.48}=+0.6928 \\ \Rightarrow r =+0.6928
Example:8.निम्नलिखित सूचनाओं से सहसम्बन्ध गुणांक (r) तथा \sigma_y के मान ज्ञात कीजिएः
(From the following information, find out the values of coefficient of correlation (r) and \sigma_y):
x=-0.167y,y=-1.5x,variance of x=25
Solution: x=-0.167 y, y=-1.5 x \\ b_{xy}=-0.167, b_{yx}=-1.5 \\ r=\sqrt{b_{xy} \times b_{yx}} \\ =\sqrt{(-0.167 \times -1.5)} \\ \Rightarrow r=\sqrt{0.2505}=0.50 \\ \sigma^2_{x}=25 \Rightarrow \sigma_x=5 \\ b_{xy}=r \frac{\sigma_x}{\sigma_y} \Rightarrow \sigma_y=\frac{r \sigma_x}{b_{xy}} \\ \Rightarrow \sigma_y=\frac{0.5 \times 5}{-0.167}=\frac{0.25}{-0.167} \\ =-1.497 \\ \Rightarrow \sigma_y \approx-1.5
Example:9.प्रस्तुत सूचनाओं से x पर y का प्रतीपगमन गुणांक ज्ञात कीजिए।
(From the given information find out regression coefficient of x on y):
N=8, \Sigma d x=56, \Sigma d y=40, \Sigma d^2 x=524, \\ \Sigma d^2 y=256, \Sigma d x d y=364
Solution: N=8, \Sigma d x=56, \Sigma d y=40, \Sigma d^2 x=524, \Sigma d^2 y=256, \Sigma dx dy=364
Regression coefficient of x on y
b_{xy}=\frac{N \cdot \Sigma d x d y-\Sigma dx \Sigma dy}{N \cdot \Sigma d^2 y-(\Sigma d y)^2} \\ =\frac{8 \times 364-56 \times 40}{8 \times 256-(40)^2} \\ =\frac{2912-2240}{2048-1600} \\ = \frac{672}{448} \\ \Rightarrow b_{xy}=1.5
Example:10.यदि x का y पर प्रतीपगमन समीकरण (Regression equation of x on y)=40x-18y=214 ,r^{2}=0.36,\sigma_{x}^2=9 हो तो y का प्रमाप विचलन (standard deviation of y) का मान ज्ञात कीजिए।
Solution: r^2=0.36, \sigma_{x}^2=9 \\ 40x-18 y=214 \\ \Rightarrow x=\frac{18 y}{40}+\frac{214}{40} \\ \Rightarrow x=\frac{9}{20} y+\frac{107}{20} \\ \Rightarrow x=0.45 y+5.35 \\ b_{xy}=0.45 \\ b_{xy}=r \frac{\sigma_x}{\sigma_y} \\ \Rightarrow 0.45=0.6 \times \frac{3}{\sigma_y} \\ \Rightarrow \sigma_y=\frac{1.8}{0.45} \\ \Rightarrow \sigma_y=4
Example:11.निम्न सूचना प्रस्तुत है
(Given the following information):
b_{yx}=2.70 Ratio of \sigma_x to \sigma_y=3: 10
Solution: b_{yx}=2.70 \quad \sigma_x to \quad \sigma_y \\ b_{yx}=r \cdot \frac{\sigma_y}{\sigma_x} \\ z=2.70 \times \frac{3}{10} \Rightarrow r=\frac{8.1}{10} \\ \Rightarrow r=0.81
व्यावहारिक प्रश्न (Numerical Questions):
Example:1.निम्नलिखित सारणी में देहली स्कन्ध विनिमय दर दो अंशों की कीमतों के माध्य तथा प्रमाप विचलन प्रदर्शित करती हैः
(The following table shows the mean and standard deviations of prices of two shares at Delhi stock exchange):
| अंश (shares) | माध्य (Mean) | प्रमाप विचलन (S.D.) |
| A LtD. | Rs. 39.5 | Rs 10.8 |
| B LtD. | Rs. 47.5 | Rs 16.8 |
यदि दोनों कीमतों में सहसम्बन्ध गुणांक +0.42 तथा B अंश की कीमत 55 रुपए है तो A अंश की सम्भाव्य कीमत ज्ञात कीजिए।
(If the coefficient of correlation in price of shares is +0.42,find the most probable price of A share when the price of B share is Rs.55.)
Solution: \overline{X}=39.5 ,\sigma_{x}=10.8, \overline{Y}=47.5 \\ \sigma_{y}=16.8,r=+0.42, Y=55 \\ X-\overline{X}=r \frac{\sigma_{x}}{\sigma_{y}}(Y-\overline{Y}) \\ \Rightarrow X-39.5=0.42 \times \frac{10.8}{16.8}(55-47.5) \\ \Rightarrow X-39.5=0.27 \times 7.5 \\ \Rightarrow X=39.5+2.025 \\ \Rightarrow X=41.525
Example:2.निम्नलिखित दिए हुए मूल्यों से Y का सम्भावित मूल्य ज्ञात कीजिए जबकि X का मूल्य 70 हो तथा X का सम्भावित मूल्य ज्ञात कीजिए जबकि Y का मूल्य 90 होः
(From the given values calculate the expected value of Y when the value of X is 70 and the expected value of X when the value of Y is 90):
| X series | Y series | |
| Mean | 18 | 100 |
| standard Deviation | 14 | 20 |
Coefficient of correlation between X and Y series=+0.8
Solution: \overline{X}=18, \overline{Y}=108,\sigma_{x}=14,\sigma_{y}=20 \\ Y-\overline{Y} =r\left(\frac{\sigma_{y}}{\sigma_{x}}\right) \left(Y-\overline{Y} \right) \\ =0.8 \times \frac{20}{14}(70-18) \\ \Rightarrow Y-100=\frac{16}{14} \times 52 \\ =\frac{832}{14} \\ =59.43 \\ \Rightarrow Y=159.43 \\ X-\overline{X}=r \frac{\sigma_x}{\sigma_y}(Y-\overline{Y}) \\ \Rightarrow X-18=0.8 \times \frac{14}{20}(90-100) \\ \Rightarrow x=18-5.6 \\ \Rightarrow x=12.4
Example:3.एक वर्ग में पति-पत्नियों की आयु का सहसम्बन्ध गुणांक +0.8 पाया गया;पतियों की औसत आयु 25 वर्ष थी और पत्नियों की 22 वर्ष थी;उनका प्रमाप विचलन क्रमशः 5 तथा 4 था।प्रतीपगमन रेखाएँ खींचिए तथा उनसे ज्ञात कीजिएः
(i)पति की सम्भावित आयु यदि पत्नी की आयु 22 वर्ष हो तथा (ii)पत्नी की आयु यदि पति की आयु 28 वर्ष हो।
(The ages of husband and wives in a community were found to have a correlation coefficient of +0.8 the average age of husbands was 25 years and average age of wives 22 years, standard deviations were 5 and 4 respectively.Draw regression lines and from the measure:(i) expected age of husband when wife’s age is 22 years and (ii)the age of wife when husband’s age is 28 years.)
Solution: r=+0.8, \overline{X}=25, \overline{Y}=22, \sigma_x=5, \sigma_y=4 \\ X-\overline{X}=r \cdot \frac{\sigma_{x}}{\sigma_{y}}(Y-\bar{Y}) \\ \Rightarrow X-25=0.8 \times \frac{5}{4}(Y-22) \\ \Rightarrow X=25+Y-22 \Rightarrow X=3+Y \\ Y-\overline{Y}=r \cdot \frac{\sigma_y}{\sigma_x}(X-\bar{X}) \\ \Rightarrow Y-22=0.8 \times \frac{4}{5}(X-25) \\ \Rightarrow Y =22+\frac{3.2}{5}(X-25) \\ =22+0.64(X-25) \\ =22+0.64 X-16 \\ \Rightarrow Y=6+0.64 X
(i)Y=22 वर्ष
X=3+Y \Rightarrow X_{22}=3+22 \Rightarrow X_{22}=25
(ii) X=28 वर्ष
Y=6+0.64 X \Rightarrow Y_{28}=6+0.64 \times 28 \\ =6+17.92\\ \Rightarrow Y_{28}=23.92
Example:4.सूचकांकों की दो श्रेणियाँ हैं D प्रयोज्य व्यक्ति की आय के लिए तथा S एक कम्पनी की बिक्री के लिए।D श्रेणी का समान्तर माध्य एवं प्रमाप विचलन क्रमशः 120 एवं 15 है तथा S श्रेणी के लिये 115 तथा 10 है।दोनों श्रेणियों के बीच सहसम्बन्ध गुणांक +0.75 है।प्रदत्त सूचना से D के विभिन्न मूल्यों का अनुमान लगाने के लिए एक रेखीय समीकरण प्राप्त कीजिए।समीकरण द्वारा D के विभिन्न मूल्यों के लिए S के मूल्यों का निर्वचन आप किस प्रकार करेंगे?क्या वही समीकरण S के विभिन्न मूल्यों का अनुमान लगाने के लिए प्रयुक्त हो सकता है?
(There are two series of Index Numbers D for disposable personal income and S for sale of a company.The mean and standard deviations of the D series are 120 and 15 respectively and of the S series 115 and 10.The coefficient between the two series is +0.75.From the given information obtain a linear equation for estimating the values of S for different values of D.How will you interpret the values of S corresponding to different values of D obtained from the equation? Can the same equation be used for estimating the values of D for different values of S?)
Solution: \bar{S}=115, \overline{D}=120, \sigma_s=10, \sigma_y=15 ,r=+0.75
S का D पर प्रतीपगमन समीकरण
S-\bar{S} =r \frac{\sigma_S}{\sigma y}(D-\bar{D}) \\ \Rightarrow S-115=0.75 \times \frac{10}{15}(D-120) \\ \Rightarrow S=115+0.5(D-120) \\ =115+0.5 D-60 \\ \Rightarrow S =55+0.5 D
No,यही समीकरण S के विभिन्न मूल्यों का अनुमान लगाने के लिए प्रयुक्त नहीं हो सकता है।
Example:5.निम्नलिखित समंकों से सहसम्बन्ध गुणांक की परिगणना कीजिए तथा दोनों प्रतीपगमन समीकरणों का निर्धारण कीजिए तथा यह बताइए कि यदि Y का मूल्य 30 हो तो X का मान बताइएः
(From the following data calculate and determine the two regression lines):
![]()
Estimate the value of X corresponding to value 30 of Y.
Solution:-Calculation Table of Regression lines
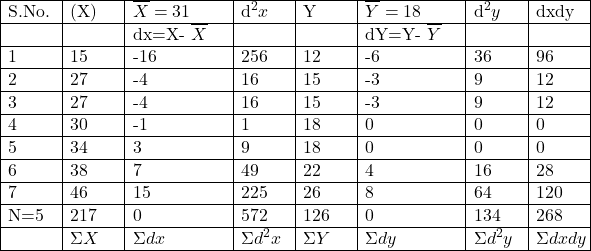
Regression coefficient X on Y
b_{xy}=\frac{\Sigma dxdy}{\Sigma d^{2}y} =\frac{268}{134}=2
Regression Equation : X on Y
X-\overline{X}=b_{xy}(Y-\bar{Y}) \\ X-31=2(Y-18) \\ \Rightarrow X=31+2 Y-36 \\ \Rightarrow X=-5+2 Y \\ \text{ Mean } \overline{Y}=\frac{\Sigma Y}{N}=\frac{126}{7}=18
Regress coefficient Y on X
b_{yx}=\frac{\Sigma dxdy}{\Sigma d^2 x}=\frac{268}{572}=0.47
Regression Equation : Y on X
Y-\bar{Y}=b_{yx}(X-\overline{X}) \\ Y-18=0.47(X-31) \\ \Rightarrow Y=18+0.47 X-14.57 \\ \Rightarrow Y=0.47 X+3.43
coefficient of correlation:
r=\sqrt{b_{xy} \times b_{yx}}=\sqrt{2 \times 0.47}=0.9695 \\ X_{30}=-5+2 \times 30 \Rightarrow X_{30}=55
उपर्युक्त उदाहरणों के द्वारा सांख्यिकी में प्रतीपगमन विश्लेषण (Regression Analysis in Statistics),सांख्यिकी में प्रतीपगमन गुणांक (Regression Coefficient in Statistics) को समझ सकते हैं।
3.सांख्यिकी में प्रतीपगमन विश्लेषण की समस्याएं (Regression Analysis in Statistics Problems):
(1.)निम्नलिखित समंक किसी परीक्षा में विषय A तथा B में प्राप्त अंकों से सम्बन्धित हैंः
(The following data are given for marks in subject A and B in a certain examination):
Coefficient of correlation A and B=+0.42
| Mean | A | B |
| Marks | 39.5 | 47.6 |
| standard Deviation | 10.8 | 16.9 |
दोनों प्रतीपगमन समीकरण ज्ञात कीजिए और यह स्पष्ट कीजिए कि प्रतीपगमन रेखाएँ दो क्यों होती हैं?A से 50 अंक पानेवाले के B में अंक अनुमानित कीजिए।
(Determine the two equations of regression and explain why there are two lines of regression.Also calculate the expected marks in B corresponding to 50 marks obtained in A.)
(2.)एक द्वि-चर बंटन के लिए निम्न माप प्रदत्त हैंः
(For a bivariate distribution the following measures are given):
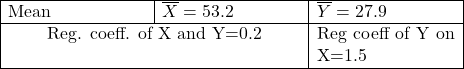
ज्ञात कीजिए (अ)X=60 के लिए Y का अनुमान (ब)सहसम्बन्ध गुणांक
Find (a)Most likely value of Y when X=60 (b)r, the correlation of coefficient
उत्तर (Answers):(1.)X=0.268Y+26.74;Y=0.657X+21.65;Y_{60}=54.5
(2.)Y=38.1,r=+0.548
उपर्युक्त सवालों को हल करने पर सांख्यिकी में प्रतीपगमन विश्लेषण (Regression Analysis in Statistics),सांख्यिकी में प्रतीपगमन गुणांक (Regression Coefficient in Statistics) को ठीक से समझ सकते हैं।
Also Read This Article:-Spearman Rank Difference Method
4.सांख्यिकी में प्रतीपगमन विश्लेषण (Frequently Asked Questions Related to Regression Analysis in Statistics),सांख्यिकी में प्रतीपगमन गुणांक (Regression Coefficient in Statistics) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.प्रतीपगमन का अर्थ बताइए। (State the Meaning of Regression):
उत्तर:प्रतीपगमन का शाब्दिक अर्थ वापसी की क्रिया अथवा पीछे लौटने (backward movement or reversion) से है।
प्रश्न:2.प्रतीपगमन शब्द का प्रयोग सर्वप्रथम किसने और कब किया? (Who and When was the Word Regression First Used?):
उत्तर:प्रतीपगमन शब्द का सर्वप्रथम प्रयोग गाल्टन (Galton) ने सन् 1877 में अपने शोध लेख “पैतृक ऊंचाई में मध्यमता की ओर प्रतीपगमन” (Regression Towards Mediocrity in Hereditary Stature) में किया था।इस शोध लेख में लगभग 1000 पिताओं तथा उनके पुत्रों की ऊंचाई (Heights) के अध्ययन के आधार पर यह निष्कर्ष निकाला गया कि यद्यपि पिता तथा पुत्रों की ऊंचाई में परस्पर घनिष्ट सहसंबंध था,लेकिन सामान्य समांतर माध्य से दोनों के विचलन में काफी अंतर पाया गया।समग्र की माध्य ऊंचाई (Mean height of the universe) से पिताओं की ऊंचाई के विचलनों की अपेक्षा पुत्रों की ऊंचाई की विचलन कम थे।दूसरे शब्दों में पिताओं की ऊंचाई समग्र की माध्य ऊँचाई से कम या अधिक होती थी लेकिन पुत्रों की ऊँचाई समग्र की माध्य ऊँचाई से काफी निकट होती जाती थी।पिताओं की अपेक्षा पुत्रों की ऊँचाई समग्र माध्य के निकट वापस जाने की इस प्रवृत्ति को ही फ्रांसिस गाल्टन ने ‘मध्यमता की ओर प्रतीपगमन’ (Regression Towards the Mean) कहा था।इस प्रवृत्ति के अनुसार यह देखने में आया कि सामान्यतः लम्बे पिताओं के पुत्र कम लंबे तथा ठिगने पिताओं के पुत्र कम ठिगने होते हैं।
प्रश्न:3.प्रतीपगमन विश्लेषण के सिद्धान्त की व्याख्या कीजिए। (Explain the Concept of Regression Analysis):
उत्तर:आधुनिक समय में प्रतीपगमन विश्लेषण की अवधारणा केवल वंशगत विशेषताओं के अध्ययन तक सीमित नहीं है वरन् इसका प्रयोग उन सभी क्षेत्रों में किया जाता है जहाँ दो या दो से अधिक श्रेणियों में विभिन्न पद-मूल्यों की समग्र माध्य (Universe Mean) की ओर वापस जाने की प्रवृत्ति पाई जाती है।प्रतीपगमन विश्लेषण के आधार पर सामाजिक,आर्थिक व व्यावसायिक क्षेत्रों में विभिन्न घटनाओं के मध्य संबंधों का विश्लेषण करके एक चर मूल्य से संबंधित दूसरा आश्रित (dependent) चर मूल्य अनुमानित किया जा सकता है।इस प्रकार आधुनिक समय में प्रतीपगमन विश्लेषण का उपयोग पूर्वानुमान या अन्तर्वेषण एवं बहिर्वेषण के उपकरण के रूप में किया जाता है।वालिस तथा राॅबर्ट्स के मतानुसार “प्रायः यह ज्ञात करना अधिक महत्त्वपूर्ण होता है कि (दो या दो से अधिक चरों में) वास्तविक सम्बन्ध क्या है जिससे एक चर-मूल्य (स्वतंत्र चर) के आधार पर दूसरे चर-मूल्य (आश्रित चर) का अनुमान लगाया जा सके और इस प्रकार की स्थिति में प्रयोग की जाने वाली उपयुक्त सांख्यिकीय रीति प्रतीपगमन विश्लेषण (Regression analysis) कहलाती है।”ब्लेयर के मतानुसार “मूल इकाइयों के रूप में दो या दो से अधिक चरों में पारस्परिक औसत संबंध का माप ही प्रतीपगमन (Regression) है।”
उपर्युक्त प्रश्नों के उत्तर द्वारा सांख्यिकी में प्रतीपगमन विश्लेषण (Regression Analysis in Statistics),सांख्यिकी में प्रतीपगमन गुणांक (Regression Coefficient in Statistics) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Regression Analysis in Statistics
सांख्यिकी में प्रतीपगमन विश्लेषण
(Regression Analysis in Statistics)
Regression Analysis in Statistics
सांख्यिकी में प्रतीपगमन विश्लेषण (Regression Analysis in Statistics) वह रीति है
जिसके माध्यम से एक चर के किसी ज्ञात मूल्य से सम्बन्धित तत्संवादी (corresponding) दूसरे
चर का सम्भाव्य मूल्य अनुमानित किया जा सकता है।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.








