Reduction of Equation of Second Degree
1.द्विघात के व्यापक समीकरण का समानयन (Reduction of Equation of Second Degree),त्रिविमीय निर्देशांक ज्यामिति में द्विघात के व्यापक समीकरण का समानयन (Reduction of General Equation of Second Degree in 3D):
द्विघात के व्यापक समीकरण का समानयन (Reduction of Equation of Second Degree) करने के लिए हम इस आर्टिकल में विभिन्न स्थितियों का अध्ययन करेंगे।
द्विघात के पद पूर्ण वर्ग हों तो व्यापक समीकरण का समानयन (Reduction of General Equation when terms of second degree form of a perfect square):
चूँकि A=B=C=0 इसलिए f(x,y,z) पूर्ण वर्ग होगा। अतः
F(x, y, z)=(\sqrt{a} x+\sqrt{b} y+\sqrt{c} z)^{2}+2 u x+2 w y+2 w z=0 \ldots(1)
(i)यदि A=B=C=F=G=H=0 तथा fu=gv=hw
ऐसी दशा में \frac{u}{\sqrt{a}}=\frac{V}{\sqrt{b}}=\frac{w}{\sqrt{c}}=K_{1} (माना)
अतः समीकरण (1) को निम्न रूप में लिखा जा सकता है:
(\sqrt{a} x+\sqrt{b} y+\sqrt{c} z)^{2}+2 k_{1}(\sqrt{a} x+\sqrt{b} y+\sqrt{c} z)+d=0 \cdots(2)
जो कि एक समान्तर समतल युग्म प्रदर्शित करता है।
(ii)यदि A=B=C=F=G=H=0 तथा f u \neq g v
इस स्थिति में \frac{u}{\sqrt{a}} \neq \frac{v}{\sqrt{b}}
इसलिए समीकरण (1) को निम्न रूप में लिखा जा सकता है:
(\sqrt{a} x+\sqrt{b} y+\sqrt{c} z+\mu)^{2}=2 x(\mu \sqrt{a}-u+ 2 y(\mu \sqrt{b}-v)+2 z(\mu \sqrt{c}-w)+\mu^{2}-d=0 \cdots(3)
अतः \mu का चयन इस प्रकार करें कि समतल
U \equiv \sqrt{a} x+\sqrt{b} y+\sqrt{c} z+\mu =0 \cdots(4)
और V \equiv 2 x(\mu \sqrt{a}-u)+2 y(\mu \sqrt{b}-v)+2 z(\mu \sqrt{C}-w)+\mu^{2}-d=0 \cdots(5)
परस्पर लम्ब हों अर्थात्
\mu=\frac{u \sqrt{a}+v \sqrt{b}+w \sqrt{c}}{a+b+c} \cdots(6)
अब यदि हम U=0 तथा V=0 समतलों को निर्देशी समतल X=0 तथा Y=0 लें तो
x=\frac{U}{\sqrt{(a+b+c)}} तथा Y=\frac{v}{2 \sqrt{\{ \Sigma (\mu \sqrt{a}-u)^{2}\}}}
तथा समीकरण (3) का विहित समघात (Canonical Form) होगा:
(a+b+c) X^{2}=2 \sqrt{\Sigma (\mu \sqrt{a}-u)^{2} Y} \\ \Rightarrow x^{2}=K_{2} Y \cdots(8)
जहाँ K_{2}= \frac{2 \sqrt{\Sigma (\mu \sqrt{a}-u)^{2}}}{(a+b+c)} \ldots(9)
उपर्युक्त पृष्ठ परवलयिक बेलन (Parabolic Cylinder) प्रदर्शित करता है।
विभिन्न स्थितियों का सारांश (Summary of different cases):
संख्यात्मक समीकरणों F(x,y,z)=0 या f(x,y,z)+2ux+2vy+2wz+d=0 का समानयन करने के लिए निम्नलिखित विधि का क्रम से उपयोग करना लाभदायक होता है:
(1.)द्वितीय घात के पूर्ण वर्ग हों (When second degree terms are perfect square):
ऐसे प्रश्नों को हल करने के लिए उपर्युक्त विधि उपयोग में लाते हैं। इसमें परवलयिक बेलन (parabolic cylinder) तथा समान्तर समतल युग्म (pair of parallel planes) आते हैं।
(2.)द्वितीय घात के पद पूर्ण वर्ग नहीं हों (When second degree terms are not perfect square):
विविक्तिकर त्रिघाती
\lambda^{3}-\lambda^{2}(a+b+c)+\lambda(A+B+C)-D=0
को हल करके \lambda_{1}, \lambda_{2} तथा \lambda_{3} के मान ज्ञात कीजिए।
(ii) यदि तीनों में से कोई भी मूल शून्य नहीं हो (अर्थात् D \neq 0) तो केन्द्र (\alpha, \beta, \gamma) समीकरणों
\frac{\partial F}{\partial x}=\frac{\partial F}{\partial y}=\frac{\partial F}{\partial z}=0
से ज्ञात कीजिए तथा मुख्य दिशाएं यदि आवश्यक हो तो
\frac{\frac{\partial f}{\partial l}}{2 l}=\frac{\frac{\partial f}{\partial m}}{2 m}=\frac{\frac{\partial f}{\partial n}}{2 n}=\lambda
से ज्ञात कीजिए। यदि दो मूल बराबर हों तो अद्वितीय मुख्य दिशा तीसरे मूल से प्राप्त होती है।
(iii)मूलबिन्दु को केन्द्र (\alpha, \beta, \gamma) पर स्थानान्तरित करने तथा अक्षों को मुख्य दिशाओं के अनुदिश घुमाने पर पृष्ठ का समीकरण
\lambda_{1} X^{2}+\lambda_{2} Y^{2}+\lambda_{3} Z^{2}+(u \alpha+v \beta+w \gamma+d)=0
द्वारा प्राप्त होगा। इसमें दीर्घवृत्तज (ellipsoid),एक पृष्ठीय अतिपरवलयज (Hyperboloid of one sheet), द्विपृष्ठी अतिपरवलयज (Hyperboloid of two sheets) एवं शंकु (Cone) आते हैं।
(iv) यदि कोई एक मूल शून्य हो (माना \lambda_{1}=0 ) तो \lambda_{1} की संगत मुख्य दिशाएँ l_{3}, m_{3}, n_{3} निम्नलिखित समीकरणों में से किन्हीं दो से ज्ञात कीजिए:
\frac{\partial f}{\partial l_{3}}-\frac{\partial f}{\partial m_{3}}=\frac{\partial f}{\partial n_{3}}=0
अब r=u l_{3}+v m_{3}+w n_{3} का मान ज्ञात कीजिए।
(v)यदि r \neq 0 तो पृष्ठ का समीकरण
\lambda_{1} X^{2}+\lambda_{2} Y^{2}+2 r z=0 से प्राप्त होगा। इसमें दीर्घवृत्तीय परवलयज (Elliptic Paraboloid) तथा अतिपरवलयिक परवलयज (Hyperbolic Paraboloid) होते हैं।
इस स्थिति में शीर्ष के निर्देशांक (\alpha, \beta, \gamma) किन्हीं दो भिन्न समीकरणों
\frac{1}{2} \frac{\partial f}{\partial x}=l_{3} r-u, \frac{1}{2} \frac{\partial f}{\partial y}=m_{3} r-v, \frac{1}{2} \frac{\partial f}{\partial z}=n_{3} r-w
तथा समीकरण
r\left(l_{3} x+m_{3} y+n_{3} z\right)+u x+v y+w z+d=0
से प्राप्त होते हैं तथा अक्ष का समीकरण
\frac{x-\alpha}{l_{3}}=\frac{y-\beta}{m_{3}}=\frac{z-\gamma}{n_{3}}
से प्राप्त होता है।
(vi) यदि r=0 तो पृष्ठ की एक केन्द्र रेखा होगी जो कि निम्नलिखित समीकरणों में से किन्हीं दो से ज्ञात कीजिए:
\frac{\partial f}{\partial x}=\frac{\partial F}{\partial y}=\frac{\partial F}{\partial z}=0
(vii) उपर्युक्त रेखा पर कोई बिन्दु को केन्द्र मानने पर पृष्ठ का समीकरण
\lambda_{1} X^{2}+ \lambda_{2} Y^{2}+(u \alpha+v \beta+w \gamma+d)=0
से प्राप्त होगा।इसमें दीर्घवृत्तीय बेलन (elliptic cylinder),अतिपरवलयिक बेलन (hyperbolic cylinder) तथा प्रतिच्छेदी समतल युग्म (pair of intersecting planes) आते हैं।
बेलन का अक्ष या समतल युग्म की प्रतिच्छेदी रेखा चूँकि केन्द्र से होकर जाते हैं तथा इसकी दिशा केन्द्र रेखा की दिशा होगी,अतः अक्ष या प्रतिच्छेदी रेखा के समीकरण होंगे:
\frac{x-\alpha}{l_{3}}=\frac{y-\beta}{m_{3}}=\frac{z-\gamma}{n_{3}}
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Centre of Conicoid in 3D
2.द्विघात के व्यापक समीकरण का समानयन के साधित उदाहरण (Reduction of Equation of Second Degree Solved Examples):
Example:1.निम्नलिखित समीकरणों का विहित रूप में समानयन कीजिए और उनसे प्रदर्शित पृष्ठ का स्वरूप ज्ञात कीजिए:
(Reduce the following equations in canonical forms and find the nature of the surface represented by it):
(i)2 y^{2}-2 y z+2 z x-2 x y-x-2 y+3 z-2=0
Solution: 2 y^{2}-2 y z+2 z x-2 x y-x-2 y+3 z-2=0 \\ a=0,b=2,c=0,f=-1,g=1,h=-1,v=-1,d=-2,u=-\frac{1}{2} \\ v=-1, w=\frac{3}{2}, d=-2 \\ A=b c-f^{2}=2 \times 0-(-1)^{2}=-1 \\ B=C a-g^{2}=0 \times 0-1^{2}=-1 \\ C=a b-h^{2}=0 \times 2-(-1)^{2}=-1 \\ D=a b c+2 f g h-a f^{2}-b g^{2}-c h^{2} \\ =0(2)(0)+2 \times(-1) \times 1 \times(-1)-0 \times(-1)^{2}-2(1)^{2}-0 \times(-1)^{2} \\ \Rightarrow D=2,-2=0
A,B,C तीनों शून्य नहीं हैं इसलिए द्विघातीय पद पूर्ण वर्ग नहीं बनाते।
अतः विविक्तिकर त्रिघाती
(i)\lambda^{3}-\lambda^{2} \cdot(a+b+c)+\lambda(A+B+C)-D=0 \\ \Rightarrow \lambda^{3}-\lambda^{2}(0+2+0)+\lambda(-1-1-1)-0=0 \\ \Rightarrow \lambda^{3}-2 \lambda^{2}-3 \lambda=0 \\ \Rightarrow \lambda\left(\lambda^{2}-2 \lambda-3\right)=0 \\ \Rightarrow \lambda\left(\lambda^{2}-3 \lambda+\lambda-3\right)=0 \\ \Rightarrow \lambda[\lambda(\lambda-3)+1(\lambda-3)]=0 \\ \Rightarrow \lambda(\lambda+1)(\lambda-3)=0 \\ \Rightarrow \lambda=-1,0,3 \\ \Rightarrow \lambda_{1}=3, \lambda_{2}=1, \lambda_{3}=0
(ii) केन्द्र के निर्देशांक (\alpha, \beta, \gamma) ज्ञात करने के लिए
\frac{\partial F}{\partial x} \equiv 2 z-2 y-1=0 \\ \frac{\partial F}{\partial y}=4 y-2 z-2 x-2=0 \\ \frac{\partial F}{\partial z}=-2 y+2 x+3=0
माना z=0 अतः y=-\frac{1}{2}, x=-2
अतः केन्द्र (\alpha, \beta, \gamma)=(-2,-\frac{1}{2},0)
(iii)u \alpha+v \beta+w \gamma+d=-\frac{1}{2} \times-2+(-1) \times -\frac{1}{2}+\frac{3}{2} \times 0-2=-\frac{1}{2} \cdots(3)
अतः मूलबिन्दु को केन्द्र पर स्थानान्तरित करने तथा निर्देशाक्षों को मुख्य दिशाओं के अनुदिश घूमने पर पृष्ठ का समीकरण निम्न रूप में प्राप्त होता है:
\lambda_{1} X^{2}+\lambda_{2} Y^{2}+\lambda_{3} Z^{2}+(u \alpha+v \beta+w r+d)=0 \\ 3 X^{2}-Y^{2}-\frac{1}{2}=0 \\ \Rightarrow 6 X^{2}-2 Y^{2}-1=0
जो कि अतिपरवलयिक बेलन है।
(ii) 2 x^{2}-7 y^{2}+2 z^{2}-10 y z-8 z x-10 x y +6 x+12 y-6 z+5=0
Solution: 2 x^{2}-7 y^{2}+2 z^{2}-10 y z-8 z x-10 x y +6 x+12 y-6 z+5=0
यहाँ a=2,b=-7,c=2,f=-5,g=-4,h=-5,u=3,v=6,w=-3,d=5
A=b c-f^{2}=-7 \times 2-(-5)^{2}=-14-25=-39 \\ B=c a-g^{2}=2 \times 2-(-4)^{2}=4-16=-12 \\ C=ab-h^{2}=2 \times-7-(-5)^{2}=-14-25=-39 \\ D=abc+2fgh-af^{2}-bg^{2}-ch^{2} \\ =2 \times -7 \times 2+2 \times -5 \times -4 \times -5 -2 \times (-5)^{2}-(-7)(-4)^{2}-2 \times (-5)^{2} \\=-28-200-50+112-50 \\ D=-216
केन्द्र के निर्देशांक के लिए
\frac{\partial F}{\partial x}=4 x-8 z-10 y+6=0 \quad \cdots(1) \\ \frac{\partial F}{\partial y}=-14 y-10 z-10 x+12=0 \cdots(2) \\ \frac{\partial F}{\partial z}=4 z-10 y-8 x-6=0 \cdots(3)
(1),(2),(3) को हल करने पर केन्द्र के निर्देशांक
(\alpha,\beta, \gamma)=\left(\frac{1}{3},-\frac{1}{3}, \frac{4}{3}\right) \\ u \alpha+v \beta+w \gamma+d=3 \times \frac{1}{3}+6 \times(-\frac{1}{3})-3 \times \frac{4}{3}+5=0
विविक्तिकर त्रिघाती
\lambda^{3}-\lambda^{2}(a+b+c)+\lambda(A+B+C)-D=0 \\ \lambda^{3}-\lambda^{2}\left(2-7+2\right)+\lambda(-39-12-39)+216=0 \\ \Rightarrow \lambda^{3}+3 \lambda^{2}-90 \lambda+216=0 \\ \Rightarrow \lambda^{3}-3 \lambda^{2}+6 \lambda^{2}-18 \lambda-72 \lambda+216=0 \\ \Rightarrow \lambda^{2}(\lambda-3)+6 \lambda(\lambda-3)-2(\lambda-3)=0 \\ \Rightarrow (\lambda-3) \left(\lambda^{2} +6 \lambda-72\right)=0 \\ \Rightarrow (\lambda-3)\left[\lambda^{2}+12 \lambda-6 \lambda-72\right]=0 \\ \Rightarrow (\lambda-3)[\lambda(\lambda+12)-6(\lambda+12)]=0 \\ \Rightarrow (\lambda-3)(\lambda-6)(\lambda+12)=0 \\ \Rightarrow \lambda=3,6,-12 \\ \lambda_{1}=3, \lambda_{2}=6, \lambda_{3}=-12
मूलबिन्दु को (\frac{1}{3},-\frac{1}{3},\frac{4}{3}) पर स्थानान्तरित करने तथा निर्देशाक्षों को मुख्य दिशा के अनुदिश घुमाने पर पृष्ठ का समीकरण निम्न रूप में प्राप्त होता है:
\lambda_{1} X^{2}+\lambda_{2} Y^{2}+\lambda_{3} Z^{2}+(u \alpha+v \beta+w \gamma+d)=0 \\ 3 X^{2}+6 Y^{2}-12 z^{2}=0 \\ \Rightarrow X^{2}+2 Y^{2}-4 z^{2}=0
जो कि शंकु को प्रदर्शित करता है।
(iii) x^{2}+y^{2}+z^{2}-2 x y-2 y z+2 z x+x-4 y+z+1=0
Solution: x^{2}+y^{2}+z^{2}-2 x y-2 y z+2 z x+x-4 y+z+1=0
यहाँ a=1,b=1,c=1,h=-1,f=-1,g=1,v=-2,d=1
u=\frac{1}{2}, v=-2, w=\frac{1}{2}, d=1 \\ A=bc-f^{2}=1 \times 1-(-1)^{2}=0 \\ B=ca-g^{2}=1 \times 1-(1)^{2}=0 \\ C=a b-h^{2}=1 \times 1-(-1)^{2}=0
इसलिए द्वितीय घात के पद पूर्ण वर्ग होंगे। दिए हुए समीकरण को निम्न प्रकार लिखा जा सकता है:
यहाँ f u-g v=-1 \times \frac{1}{2}-1 \times-2 \neq 0
(x-y+z+\mu)^{2}=2 x(\mu-\frac{1}{2})-2 y(\mu-2) +2 z(\mu-\frac{1}{2})+\mu^{2}-1=0 \\ \Rightarrow(x-y+z+\mu)^{2}=(2 \mu-1) x+(2\mu-4) y+(2 \mu-1) z+\mu^{2}-1=0 \quad \ldots(2)
अब \mu का चयन इस प्रकार करते हैं कि समतल
x-y+z+\mu=0 तथा (2 \mu-1) x+ (2 \mu+4) y+(2 \mu-1) z+\mu^{2}-1=0
परस्पर लम्ब हों अर्थात्
1(2 \mu-1)+1(2 \mu-4)+1(2 \mu-1)=0 \\ \Rightarrow 2 \mu-1+2 \mu-4+2 \mu-1=0 \\ \Rightarrow \mu=1
का मान (2) में रखने पर:
\Rightarrow(x-y+z+1)^{2}=x+2y+z \\ \Rightarrow 3\left(\frac{x-y+z+1}{\sqrt{3}}\right)^{2} =\sqrt{6}\left(\frac{x+2 y+z}{\sqrt{6}}\right) \\ \Rightarrow 3 Y^{2}=\sqrt{6} X
जो कि परवलयिक बेलन को प्रदर्शित करता है :
(iv) 6 y^{2}-18 y z-6 z x+2 x y-9 x+5 y-5 z+2=0
Solution: 6 y^{2}-18 y z-6 z x+2 x y-9 x+5 y-5 z+2=0
यहाँ a=0, b=6, c=0, f=-9, g=-3, h=1, u=-\frac{9}{2} \\ v=\frac{5}{2}, w=-\frac{5}{2}, d=2 \\ A=b c-f^{2}=6 \times 0-(-9)^{2}=-81 \\ B=c a-g^{2}=0 \times 0-(-3)^{2}=-9 \\ C=a b-h^{2}=0 \times 6-(1)^{2}=-1 \\ D=a b c+2 f g h-a f^{2}-b g^{2}-c h^{2} \\=0 \times 6 \times 0+2 \times-9 \times-3 \times 1-0 \times(-9)^{2}-6(-3)^{2}-0(1) \\ \Rightarrow D=54-54=0
A,B,C तीनों शून्य नहीं हैं इसलिए द्विघातीय पद पूर्ण वर्ग नहीं बनाते।
अतः विविक्तिकर त्रिघाती
\lambda^{3}-\lambda^{2}(a+b+C)+\lambda(A+B+C)-D=0 \\ \lambda^{3}-\lambda^{2}(6+6+0)+\lambda(-81-9-1)-0=0 \\ \Rightarrow \lambda^{3}-6 \lambda^{2}-91 \lambda=0 \\ \Rightarrow \lambda\left(\lambda^{2}-6 \lambda-91\right)=0 \\ \Rightarrow \lambda\left[\lambda^{2}-13 \lambda+7 \lambda-91\right]=0 \\ \Rightarrow \lambda[\lambda(\lambda-13)+7(\lambda-13)]=0 \\ \Rightarrow \lambda(\lambda-13)(\lambda+7)=0 \\ \Rightarrow \lambda=0,13,-7 \quad \lambda_{1}=-7, \lambda_{2}=13 ,\lambda_{3}=0
(ii) \lambda_{3}=0 के संगत मुख्य दिशा l_{3}, m_{3}, n_{3} ज्ञात करने के लिए
f\left(l_{3}, m_{3}, n_{3}\right)=6 m_{3}^{2}-18 m_{3} n_{3}-6 n_{3} l_{3} +2 l_{3} m_{3}\\ \frac{\partial f}{\partial l_{3}}=\frac{\partial f}{\partial m_{3}}=\frac{\partial f}{\partial n_{3}}=0 \\ \Rightarrow-6 n_{3}+2 m_{3}=0 \\ \Rightarrow 12 m_{3}-18 m_{3}+2 m_{3}=0 \\ \Rightarrow -18 m_{3}-6 l_{3}=0
प्रथम दो से
(iii) r=u l_{3}+v m_{3}+w n_{3} \\ =-\frac{9}{2} \times \frac{9}{\sqrt{91}}+\frac{5}{2} \times \frac{-3}{\sqrt{91}}-\frac{5}{2} \times \frac{-1}{\sqrt{91}} \\ r=\frac{1}{\sqrt{91}}\left[-\frac{81}{2}-\frac{15}{2}+\frac{5}{2}\right]=- \frac{\sqrt{91}}{2}
(iv)चूँकि r \neq 0 ऐसी दशा में केन्द्र अनन्त दूरी पर होगा। अतः मूलबिन्दु को शीर्ष पर स्थानान्तरित करने तथा निर्देशाक्षों को मुख्य दिशाओं की ओर घुमाने से पृष्ठ का समीकरण निम्न होगा:
\lambda_{1} X^{2}+\lambda_{2} Y^{2}+2 r z=0 \\ -7 X^{2}+13 Y^{2}+2\left(-\frac{\sqrt{91}}{2}\right) Z=0 \\ \Rightarrow 14 X^{2}-26 Y^{2}+2 \sqrt{91} Z=0
जो कि अतिपरवलयिक परवलयज को प्रदर्शित करता है।
(v) 4 x^{2}+9 y^{2}+36 z^{2}-36 y z+24 z x-12 x y -10 x+15 y-30 z+6=0
Solution: 4 x^{2}+9 y^{2}+36 z^{2}-36 y z+24 z x-12 x y -10 x+15 y-30 z+6=0
यहाँ a=4, b=9, c=36,8=-18, g=12, \\ h=-6,4=-5, v=\frac{15}{2}, w=-15, d=6 \\ A=b c-f^{2}=36 \times 9-(-18)^{2}=324-324=0 \\ B=c a-g^{2}=36 \times 4-(12)^{2}=144-144=0 \\ C=a b-h^{2}=4 \times 9-(-6)^{2}=36-36=0
इसलिए द्वितीय घात के पद पूर्ण वर्ग होंगे। दिए हुए समीकरण को निम्न प्रकार लिखा जा सकता है:
(2 x-3 y+6 z)^{2}-10 x+15 y-30 z+6=0 \cdots(1)
यहाँ fu-gv=-18 \times-5-12 \times \frac{15}{2}=90-90=0
अतः (1) का स्वरूप होगा:
(2 x-3 y+6 z)^{2}-5(2 x-3 y+6 z)+6=0 \\ 49\left(\frac{2 x-3 y+6 z}{\sqrt{49}}\right)^{2} -35\left(\frac{24(-3 y+6 z}{\sqrt{49}}\right)+6=0
जो कि निम्नलिखित समान्तर समतल युग्म को प्रदर्शित करता है:
49 X^{2}-35 X+6=0
(vi) 20 x^{2}+20 y^{2}+18 z^{2}-2 y z+12 x y+22 x+6 y-2 z-2=0
Solution: 20 x^{2}+20 y^{2}+18 z^{2}-2 y z+12 x y+22 x+6 y-2 z-2=0
यहाँ a=2,b=20,c=18,f=-6,h=6,g=0, u=11,v=3,w=-1,d=2
A=bc-f^{2}=20 \times 18-(-6)^{2}=360-36=324 \\ B=ca-g^{2}=18 \times 2-(c)^{2}=36 \\ C=a b-h^{2}=2 \times 20-6^{2}=40-36=4 \\ D= a b c+2 f g h-a f^{2}-b y^{2}-c h^{2} \\ = 2 \times 20 \times 18+2 \times-6 \times 0 \times 6-2 \times(-6)^{2} -20 \times 0^{2}-18 \times 6^{2} \\ \Rightarrow D= 720-72-648=0
A,B,C तीनों शून्य नहीं हैं इसलिए द्विघातीय पद पूर्ण वर्ग नहीं बनाते।
(i)अतः विविक्तिकर त्रिघाती
\lambda^{3}-\lambda^{2}(a+b+c)+\lambda(A+B+C)-D=0 \\ \Rightarrow \lambda^{3}-\lambda^{2}(2+20+18)+\lambda(324+36+4)-0+0 \\ \Rightarrow \lambda^{3}-40 \lambda^{2}+364 \lambda=0 \\ \Rightarrow \lambda\left(\lambda^{2}-40 \lambda+364\right)=0 \\ \Rightarrow \lambda\left[\lambda^{2} -26 \lambda-14 \lambda+364\right]=0 \\ \Rightarrow \lambda[\lambda(\lambda-26)-14(\lambda-26)]=0 \\ \Rightarrow \lambda(\lambda-14)(\lambda-26)=0 \\ \Rightarrow \lambda=0,14,26 \\ \lambda_{1}=14, \lambda_{2}=26, \lambda_{3}=0
(ii) \lambda_{3}=0 के संगत मुख्य दिशा l_{3}, m_{3}, n_{3} ज्ञात करने के लिए
f\left(l_{3}, m_{3}, n_{3}\right)=2 l_{3}^{2}+20 m_{3}^{2}+18 m_{3}^{2} -12 m_{3} n_{3}+12 l_{3} m_{3} \\ \frac{\partial f}{\partial l_{3}}=\frac{\partial f}{\partial m_{3}}=\frac{\partial f}{\partial m_{3}}=0 \\ \Rightarrow l_{3}+3 m_{3}+0 n_{3}=0 \\ 3 l_{3}+10 m_{3}-3 n_{3}=0 \\ 0 l_{3}-m_{3}+3 n_{3}=0
प्रथम दो से:
(iii)r=u l_{3}+v m_{3}+w n_{3} \\ =11 \times-\frac{9}{\sqrt{91}}+3 \times \frac{3}{\sqrt{91}}-1 \times \frac{1}{\sqrt{91}} \\ =\frac{1}{\sqrt{9}}[-99+9-1]=-\sqrt{91} \neq 0 \\ \Rightarrow r =-\sqrt{91} \neq 0
(iv)चूँकि r \neq 0 ऐसी दशा में केन्द्र अनन्त दूरी पर होगा। अतः मूलबिन्दु को शीर्ष पर स्थानान्तरित करने तथा निर्देशाक्षों को मुख्य दिशाओं की ओर घुमाने से पृष्ठ का समीकरण निम्न होगा:
\lambda_{1} X^{2}+\lambda_{2} Y^{2}+2 rz=0 \\ \Rightarrow 14 X^{2}+26 Y^{2}-2 \sqrt{91} Z=0
जो दीर्घवृतीय परवलयज को प्रदर्शित करता है।
उपर्युक्त उदाहरणों के द्वारा द्विघात के व्यापक समीकरण का समानयन (Reduction of Equation of Second Degree),त्रिविमीय निर्देशांक ज्यामिति में द्विघात के व्यापक समीकरण का समानयन (Reduction of General Equation of Second Degree in 3D) को समझ सकते हैं।
3.द्विघात के व्यापक समीकरण का समानयन के सवाल (Reduction of Equation of Second Degree Questions):
(1.)सिद्ध करो कि पृष्ठ के समीकरण 3x^{2}+4 y^{2}+9 z^{2}+12 y z+6 z x+4 x y+4 x +6 y+2 z+1=0 का समानयन दीर्घवृत्तीय परवलयज में होता है
(Prove that reduction of surface represented by the equation 3x^{2}+4 y^{2}+9 z^{2}+12 y z+6 z x+4 x y+4 x +6 y+2 z+1=0 is an elliptic Paraboloid).
(2.)2 x^{2}+5 y^{2}+2 z^{2}-2 y z+4 z x-2 x y+14 x -16 y+14 z+26=0 का मानक रूप में समानयन करो
(Reduce 2 x^{2}+5 y^{2}+2 z^{2}-2 y z+4 z x-2 x y+14 x -16 y+14 z+26=0 to the standard form)
उत्तर (Answers):(1) [8+\sqrt{38}] x^{2}+[8-\sqrt{38}] y^{2}-\left [ \frac{14}{\sqrt{13}} \right ] z=0
(2) 2 x^{2}+y^{2}=1
उपर्युक्त सवालों को हल करने पर द्विघात के व्यापक समीकरण का समानयन (Reduction of Equation of Second Degree),त्रिविमीय निर्देशांक ज्यामिति में द्विघात के व्यापक समीकरण का समानयन (Reduction of General Equation of Second Degree in 3D) को ठीक से समझ सकते हैं।
Also Read This Article:-Reduction of Equation of 2nd Degree 3D
4.द्विघात के व्यापक समीकरण का समानयन (Reduction of Equation of Second Degree),त्रिविमीय निर्देशांक ज्यामिति में द्विघात के व्यापक समीकरण का समानयन (Reduction of General Equation of Second Degree in 3D) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.द्विपृष्ठी अतिपरवलयज की आकृति कैसी होती है? (What is the shape of Hyperboloid of two sheets?):
उत्तर:द्विपृष्ठी अतिपरवलयज (Hyperboloid of two sheets) की आकृति निम्न है:
प्रश्न:2.दीर्घवृत्तीय अतिपरवलयज की आकृति कैसी होती हैं? (How is the shape of elliptic Paraboloid?):
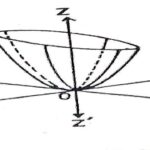
उत्तर:दीर्घवृत्तीय अतिपरवलयज (elliptic Paraboloid) की आकृति निम्न प्रकार की होती है :
प्रश्न:3.अतिपरवलयिक परवलयज की आकृति कैसी होती है? (How is the shape of hyperbolic Paraboloid?):

उत्तर:अतिपरवलयिक परवलयज (hyperbolic Paraboloid) की आकृति निम्न प्रकार की होती है:
उपर्युक्त प्रश्नों के उत्तर द्वारा द्विघात के व्यापक समीकरण का समानयन (Reduction of Equation of Second Degree),त्रिविमीय निर्देशांक ज्यामिति में द्विघात के व्यापक समीकरण का समानयन (Reduction of General Equation of Second Degree in 3D) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Reduction of Equation of Second Degree
द्विघात के व्यापक समीकरण का समानयन
(Reduction of Equation of Second Degree)
Reduction of Equation of Second Degree
द्विघात के व्यापक समीकरण का समानयन (Reduction of Equation of Second Degree) करने
के लिए हम इस आर्टिकल में विभिन्न स्थितियों का अध्ययन करेंगे।








