Radial and Transverse Acceleration
1.अरीय एवं अनुप्रस्थ त्वरण (Radial and Transverse Acceleration),अरीय एवं अनुप्रस्थ वेग (Radial and Transverse Velocities):
अरीय एवं अनुप्रस्थ त्वरण (Radial and Transverse Acceleration) पर आधारित सवाल हल करेंगे।इसके अलावा अरीय एवं अनुप्रस्थ वेग पर आधारित उदाहरणों का भी अध्ययन करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Kepler Laws for Planetary Motion
2.अरीय एवं अनुप्रस्थ त्वरण के उदाहरण (Radial and Transverse Acceleration Examples):
Example:1.यदि एक कण a त्रिज्या के वृत्त की परिधि पर गमन करता है तो वृत्त के केन्द्र को ध्रुव मानते हुए कण का अरीय वेग लिखिए।
(If a particle is moving along the circle of radius a and centre of the circle be taken as pole then write the radial velocity of the particle.)
Solution:r=a (अचर)
अतः अरीय वेग \frac{d y}{d t}=0
Example:4.यदि एक कण इस प्रकार गमन करता है कि उसका अरीय एवं अनुप्रस्थ वेग सदैव समान हो,तो इसके वक्र का समीकरण ज्ञात कीजिए।इसी के साथ यदि कण का कोणीय वेग अचर हो,तो अरीय और अनुप्रस्थ त्वरण के बारे में व्याख्या कीजिए।
(If a particle moves in such a way that its radial and transverse velocities are equal then find the equation of its path.If in addition the angular velocity of the particle is constant then explain about radial and transverse acceleration.)
Solution:\frac{d r}{d t}=r \frac{d \theta}{d \theta} \cdots(1) \\ \Rightarrow \quad \frac{d r}{r}=d \theta
समाकलन करने पर:
\log r=\theta+\log k \\ \Rightarrow \log \frac{r}{k}=\theta \\ \Rightarrow r=k e^\theta
जो कि समानकोण सर्पिल है।
यदि \frac{d \theta}{d t}=c (अचर हो तो)
\frac{d^2 \theta}{d t^2}=\ddot{\theta}=0 \\ \frac{d r}{d t}=r c \\ \frac{d^2 r}{d t^2}=c
अरीय त्वरण=\ddot{r}-r \dot{\theta}^2 \\ =c-r(c)^2 \\ =c-r c^2
अनुप्रस्थ त्वरण =2 \dot{r} \dot{\theta}+r \ddot{\theta} \\ =2(r c) c+r(0) \\=2 r c^2
Example:6.एक कण एकसमान कोणीय वेग से वक्र r=a e^\theta में चलता है।सिद्ध करो कि इसका अरीय त्वरण शून्य होगा तथा अनुप्रस्थ त्वरण इसकी ध्रुव से दूरी के समानुपाती होगा।
(A particle describes the curve r=a e^\theta with constant angular velocity.Show that its radial acceleration is zero and transverse acceleration varies as its distance from the pole.)
Solution:कोणीय वेग =\frac{d \theta}{d t}=\omega \\ r=a e^\theta \\ \Rightarrow \frac{d r}{d t}=a e^{\theta} \frac{d \theta}{dt}\\ =a \omega e^\theta \\ -\frac{d^2 r}{d t^2}=a \omega e^\theta \frac{d \theta}{d t}=a \omega^2 e^\theta
अरीय त्वरण=\frac{d^2 r}{d t^2}-r \left(\frac{d \theta }{d t}\right)^2 \\ =a \omega^2 e^\theta-a e^\theta \cdot \omega^2 \\=0
अनुप्रस्थ त्वरण=\frac{1}{r} \frac{d}{d t}\left[r^2 \frac{d \theta}{d t}\right] \\ =\frac{1}{r} \frac{d}{d t}\left[r^2 \omega\right]=\frac{\omega}{r} 2 r \frac{d r}{d t} \\ =2 \omega \cdot \omega r=2 \omega^2 r \\ \text{अनुप्रस्थ त्वरण } \propto r
अतः अनुप्रस्थ त्वरण ध्रुव से दूरी r के समानुपाती है।
Example:8.एक बिन्दु किसी वक्र में अचर वेग से चलता है और इसका किसी दिए हुए स्थिर बिन्दु O के सापेक्ष कोणीय वेग इसकी O से दूरी का व्युत्क्रमानुपाती है।सिद्ध करो कि वक्र एक समानकोणिक सर्पिल है।
(A particle describes a curve with constant velocity and its angular velocity about a given fixed point O varies inversely as its distance from O. Show that the curve is equiangular spiral.)
Solution:दिया है v=k
तथा \frac{d \theta}{d t}=\frac{c}{r} (जहाँ O ध्रुव तथा OP=r)… (1)
v=\sqrt{\left(\frac{d r}{d t}\right)^2+r^2\left(\frac{d \theta}{d t}\right)^2}=k \cdots(2)
(1) को (2) से
\Rightarrow \sqrt{\left(\frac{d r}{d t}\right)^2+r^2 \cdot \frac{c^2}{r^2}}=k \\ \Rightarrow \left(\frac{d r}{d t}\right)^2+c^2=k^2 \\ \Rightarrow\left(\frac{d r}{d t}\right)^2=k^2-c^2 \\ \Rightarrow\left(\frac{d r}{d t}\right)^2=A^2\left[k^2 c^2=A^2\right] \\ \Rightarrow \frac{d r}{d t}=A \quad \ldots(3)
(1) को (3) से विभाजित करने पर:
\frac{d r}{d \theta}=\frac{A r}{c} \\ \Rightarrow \frac{d r}{r}=\frac{A}{c} d \theta
समाकलन करने पर:
\int \frac{d r}{r}=\frac{A}{c} \int d \theta \\ \Rightarrow \log r=\frac{A}{c} \theta+\log B \\ \Rightarrow \log \left(\frac{r}{B}\right)=\frac{A}{c} \theta \\ \Rightarrow r=B e^{\frac{A}{C} \theta}
जो कि समानकोणिक सर्पिल है।
Example:11.यदि एक बिन्दु किसी वृत्त में चलता हो तो सिद्ध करो कि उसकी परिधि पर किसी बिन्दु के सापेक्ष कोणीय वेग,केन्द्र के सापेक्ष कोणीय वेग का आधा होता है।
(If a point moves along a circle.Prove that its angular velocity about any point on the circumference of the circle is half of that about the centre.)
Solution:हम जानते हैं कि यदि परिधि पर कोण हो तो कोई भी चाप केन्द्र पर कोण बनाता है।
अतः परिधि पर कोणीय वेग=\frac{d \theta}{d t}
केन्द्र पर कोणीय वेग=\frac{d}{d t}(2 \theta)=2 \frac{d \theta}{d t}
अतः केन्द्र के सापेक्ष कोणीय वेग,परिधि पर किसी बिन्दु के सापेक्ष कोणीय का दुगुना होता है।
Example:12.सिद्ध करो कि एक बिन्दु P का बिन्दुपथ जिसके दो अचर वेग u तथा v,पहला किसी स्थिर दिशा में और दूसरा एक बिन्दु से खींची गई त्रिज्या OP के लम्बवत है,शांकव होगा जिसकी नाभि O तथा उत्केन्द्रता \frac{u}{v} है।
(Show that the path of a point P which possesses two constant velocities u and v, the first of which is in a fixed direction and the other is perpendicular to the radius OP drawn from a fixed point O, is a conic whose focus is O and whose eccentricity \frac{u}{v})
Solution:माना स्थिर दिशा प्रारम्भिक दिशा की तरफ है।इस दिशा में वेग u है।अनुप्रस्थ वेग v दिया गया है।u का ध्रुवीय रेखा की दिशा में घटक जबकि ध्रुवान्तर रेखा के लम्बवत दिशा में घटक होगा।
अतः \frac{d r}{d t}=u \cos \theta \cdots(1) \\ r \frac{d \theta}{d t}=r-u \sin \theta \cdots(2)
(3) को (1) से विभाजित करने पर:
समाकलन करने पर:
\int \frac{d r}{r}=\int \frac{u \cos \theta}{v-u \sin \theta} d \theta\\ \log r=-\log (v-u \sin \theta)+ \log k \\ \Rightarrow \log k-\log r=\log (v-u \sin \theta) \\ \Rightarrow \log \left(\frac{k}{r}\right)=\log (v-u \sin \theta) \\ \Rightarrow \frac{k}{r}=v-u \sin \theta \\ \Rightarrow \frac{\left(\frac{k}{v}\right)}{r}=1-\frac{u}{v} \sin \theta
अतः \frac{k}{v} अर्ध नाभिलम्ब तथा \frac{u}{v} उत्केन्द्रता है और O नाभि है।
Example:13.यदि एक समतल वक्र में किसी गतिमान कण के त्वरण को ऐसे दो घटकों में वियोजित किया जाता है कि उनमें से एक प्रारम्भिक रेखा के समान्तर तथा दूसरा ध्रुवान्तर रेखा की दिशा में है,तो सिद्ध कीजिए कि वे भाग निम्न होंगे:
(If the acceleration of a particle describing a plane curve is resolved into two components, one parallel to the initial line and the other along the radius vector.Prove that these components are:
-\frac{1}{r \sin \theta} \frac{d}{d r}\left(r^2 \frac{d \theta}{d t}\right) \text { and } \frac{d^2 r}{d t^2}-r\left(\frac{d \theta}{d t}\right)^2+\frac{\cot \theta}{r} \frac{d}{d t}\left(r^2 \frac{d \theta}{d t}\right)
Solution:अरीय त्वरण =\frac{d^2 r}{d t^2}-r\left(\frac{d \theta}{d t}\right)^2
अनुप्रस्थ त्वरण=2\left(\frac{d r}{d t}\right)\left(\frac{d \theta}{d r}\right)+r\left(\frac{d^2 \theta}{d t^2}\right)
माना कि ध्रुवान्तर रेखा तथा प्रारम्भिक रेखा की तरफ त्वरण F_1 तथा F_2 हैं। F_2 ,Op के लम्ब तथा अरीय त्वरण के घटक में जोड़ने पर
F_1+F_2 \cos \theta=\frac{d^{2}r}{d t^2}-r \left(\frac{d \theta}{d t}\right)^2 \cdots(1) \\ -F_2 \sin \theta=\frac{1}{r} \frac{d}{d t}\left(r^2 \dot{\theta} \right) \cdots(2) \\ F_2=-\frac{1}{r \sin \theta} \frac{d}{d t}\left(r^2 \frac{d \theta}{d t}\right) \cdots(3)
F_2 का मान (1) में रखने पर:
F_1-\frac{1}{r \sin \theta} \cos \theta \frac{d}{d t}\left(r^2 \frac{d \theta}{d t}\right)=\frac{d^2 r}{d t^2}-r\left ( \frac{d \theta}{d t} \right)^2 \\ \Rightarrow F_1=\frac{\cot \theta}{r} \frac{d}{d t}\left(r^2 \frac{d \theta}{d t}\right)+\frac{d^2 r}{d t^2}-r \left(\frac{d \theta}{d t}\right)^2
Example:14.एक सीधा व चिकना ट्यूब अपने एक स्थिर सिरे के सापेक्ष एक समान कोणीय वेग w से क्षैतिज तल में घूमता है।यदि शून्य समय पर इसके अन्दर एक कण स्थिर सिरे से a दूरी पर हो और ट्यूब के सहारे V वेग से चल रहा हो तो सिद्ध करो कि t समय पर इसकी दूरी a \cosh \omega t+\left ( \frac{u}{\omega} \right ) \sinh \omega t होगी।
(A straight smooth tube revolves with angular velocity w in a horizontal plane about one extremity which is fixed;if at zero time a particle inside it be at a distance a from the fixed end and moving with velocity V along the tube;show that its distance at time t is a \cosh \omega t+\left ( \frac{u}{\omega} \right ) \sinh \omega t )
Solution:माना कि ट्यूब की प्रारम्भिक स्थिति OX के अनुदिश है और O ट्यूब में ध्रुव है,t समय पश्चात माना कि कण ट्यूब P बिन्दु पर है।
कण ट्यूब के साथ अचर वेग V से चल रहा है अतः अरीय वेग सम्पूर्ण गति के दौरान शून्य होगा
\frac{d^2 r}{d t^2}-r\left(\frac{d v}{d t}\right)^2=0 \cdots(1)
दिया है \frac{d \theta}{d t}=w \cdots(2)
(1) व (2) से
\frac{d^2 r}{d t^2}-r \omega^2=0 \\ \left(D^2-\omega^2\right) r=0
यह अवकल समीकरण है जिसका हल है
r=A \cosh \omega t+B \sin \omega t \cdots(3)
जब t=0,r=a तो (3) से:
A=a
(3) का पुनः अवकलन करने पर:
\frac{d r}{d t}=A \omega \sin \omega t+B \omega \cosh \omega t
जब t=0,तब \frac{d r}{d t}=V \\ B=\frac{v}{w}
(3) में A व B का मान रखने पर:
r=a \cos h \omega t+\left(\frac{v}{\omega}\right) \sin \omega t
उपर्युक्त उदाहरणों के द्वारा अरीय एवं अनुप्रस्थ त्वरण (Radial and Transverse Acceleration),अरीय एवं अनुप्रस्थ वेग (Radial and Transverse Velocities) को समझ सकते हैं।
3.अरीय एवं अनुप्रस्थ त्वरण के सवाल (Radial and Transverse Acceleration Questions):
(1.)एक छोटा मणिका कार्डिआइड r=a(1+\cos \theta) आकार के चिकने तार पर अचर वेग v से फिसलता है।सिद्ध करो कि \frac{d \theta}{d t} का मान \frac{v \sec \frac{\theta}{2}}{2 a} और त्वरण का अरीय घटक अचर है।
(A small bead slides with constant speed v on a smooth wire in the shape of the cardiode r=a(1+ \cos \theta) .Show that the value of \frac{d \theta}{d t} is \frac{v \sec \frac{\theta}{2}}{2 a} and that the radical component of the acceleration is constant.)
(2.)एक बिन्दु परवलय \frac{2 a}{r}=1+\cos \theta पर इस प्रकार गति करता है कि नाभि से ध्रुवान्तर रेखा पर वेग का घटक 90° पर अचर है।सिद्ध करो कि बिन्दु पर त्वरण परिणाम में अचर है।
(A point moves on a parabola \frac{2 a}{r}=1+\cos \theta in such a manner that the component of velocity at right angle to the radius vector from the focus is constant. Show that the acceleration of the point is constant in magnitude.)
उपर्युक्त सवालों को हल करने पर अरीय एवं अनुप्रस्थ त्वरण (Radial and Transverse Acceleration),अरीय एवं अनुप्रस्थ वेग (Radial and Transverse Velocities) को ठीक से समझ सकते हैं।
Also Read This Article:-Laws of Kepler for Planetary Motion
4.अरीय एवं अनुप्रस्थ त्वरण (Frequently Asked Questions Related to Radial and Transverse Acceleration),अरीय एवं अनुप्रस्थ वेग (Radial and Transverse Velocities) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.अरीय वेग के सूत्र को स्थापित करो। (Establish the Formula of Radial Velocity):
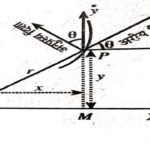
उत्तर:हम निर्देशांक्षों के समान्तर वेग तथा त्वरण से अरीय एवं अनुप्रस्थ त्वरण ज्ञात कर सकते हैं।
x=r \cos \theta, y=r \sin \theta \\ \dot{x}=\dot{r} \cos \theta-r \sin \theta \cdot \dot{\theta} तथा \dot{y}=\dot{r} \sin \theta+r \cos \theta \cdot \dot{\theta} \\ \ddot{x}=\ddot{r} \cos \theta-2 \dot{r} \dot{\theta} \sin \theta-r \dot{\theta}^{2} \cdot \cos \theta-r \ddot{\theta} \sin \theta तथा \ddot{y}=\ddot{r} \sin \theta+2 \dot{r} \dot{\theta} \cos \theta-r \dot{\theta}^2 \sin \theta+r \ddot{\theta} \cos \theta
अब वेग \dot{x} तथा \dot{y} को अरीय तथा अनुप्रस्थ दिशाओं में वियोजित करने पर:
अरीय वेग (Radial Velocity):-
=\dot{x} \cos \theta+\dot{y} \sin \theta \\ = (\dot{r} \cos \theta-r \sin \theta \cdot \dot{\theta}) \cos \theta+(\dot{r} \sin \theta +r \cos \theta \cdot \dot{\theta}) \sin \theta \\= \dot{r}\left(\cos ^2 \theta+\sin^2 \theta\right)=\dot{r}
प्रश्न:2.अनुप्रस्थ वेग के सूत्र को स्थापित करो। (Establish the Formula of Transverse Velocity):
उत्तर:अनुप्रस्थ वेग (Transverse Velocity):
=\dot{y} \cos \theta-\dot{x} \sin \theta \\ =(r \sin \theta-r \cos \theta \cdot \dot{\theta}) \cos \theta-(\dot{r} \cos \theta -r \sin \theta \cdot \dot{\theta}) \sin \theta \\ =r\left(\sin ^2 \theta+\cos ^2 \theta\right)=r \dot{\theta}
प्रश्न:3.अरीय त्वरण को स्थापित करो। (Establish the Formula of Radical Acceleration):
उत्तर:अरीय त्वरण (Radical Acceleration):
=\ddot{x} \cos \theta+\ddot{y} \sin \theta \\ =(\ddot{r} \cos \theta-2 \dot{r} \dot{\theta} \sin \theta-r \dot{\theta} \cos \theta-r \ddot{\theta}\sin \theta) \cos \theta+\left(\ddot{r} \sin \theta+2 \dot{r} \dot{\theta} \cos \theta-r \dot{\theta}^2 \sin \theta+r \ddot{\theta} \cos \theta\right) \sin \theta \\ =\ddot{r}\left(\cos ^2 \theta+\sin ^2 \theta\right)-r \dot{\theta}^2\left(\cos ^2 \theta+ \sin^2 \theta \right) \ =\ddot{r}-r \dot{\theta}^2
उपर्युक्त प्रश्नों के उत्तर द्वारा अरीय एवं अनुप्रस्थ त्वरण (Radial and Transverse Acceleration),अरीय एवं अनुप्रस्थ वेग (Radial and Transverse Velocities) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Radial and Transverse Acceleration
अरीय एवं अनुप्रस्थ त्वरण
(Radial and Transverse Acceleration)
Radial and Transverse Acceleration
अरीय एवं अनुप्रस्थ त्वरण (Radial and Transverse Acceleration) पर आधारित सवाल हल
करेंगे।इसके अलावा अरीय एवं अनुप्रस्थ वेग पर आधारित उदाहरणों का भी अध्ययन करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.









