Quadrilaterals Class 9
1.चतुर्भुज कक्षा 9 (Quadrilaterals Class 9),कक्षा 9 में चतुर्भुज (Quadrilaterals in Class 9):
चतुर्भुज कक्षा 9 (Quadrilaterals Class 9)में चतुर्भुज वह आकृति है जो चारों बिन्दुओं को एक क्रम में जोड़ने से प्राप्त होती है।आप अपने परिवेश (चारों ओर) में, अपने आसपास चतुर्भुज के आकार की अनेक वस्तुएँ देख सकते हैं जैसेःआपकी कक्षा का फर्श,दीवार,छत,खिड़कियाँ,श्यामपट्ट,डस्टर (duster) का प्रत्येक फलक,आपकी पुस्तक का प्रत्येक पृष्ठ,पढ़ने की मेज का ऊपरी पृष्ठ इत्यादि।
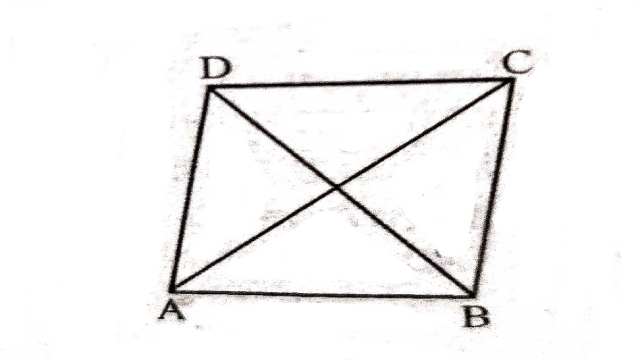
प्रमेय (Theorem):8.1.किसी समान्तर चतुर्भुज का एक विकर्ण उसे दो सर्वांगसम त्रिभुजों में विभाजित करता है।
दिया है (Given):विकर्ण AC समान्तर चतुर्भुज ABCD को दो त्रिभुजों ![]() और
और ![]() में विभाजित करता है।
में विभाजित करता है।
सिद्ध करना है (To Prove): ![]()
उपपत्ति (Proof): ![]() और AC तिर्यक रेखा इनको काटती है।अतः
और AC तिर्यक रेखा इनको काटती है।अतः![]() (एकान्तर कोण)
(एकान्तर कोण)
इसी प्रकार ![]() तथा तिर्यक रेखा AC इनको काटती है।अतः
तथा तिर्यक रेखा AC इनको काटती है।अतः![]() (एकान्तर कोण)
(एकान्तर कोण)
अब ![]() और
और ![]() में
में![]() (सिद्ध किया है)
(सिद्ध किया है)![]() (सिद्ध किया है)
(सिद्ध किया है)
AC=AC (उभयनिष्ठ भुजा है)
अतः ASA सर्वांगसमता गुणधर्म से
![]()
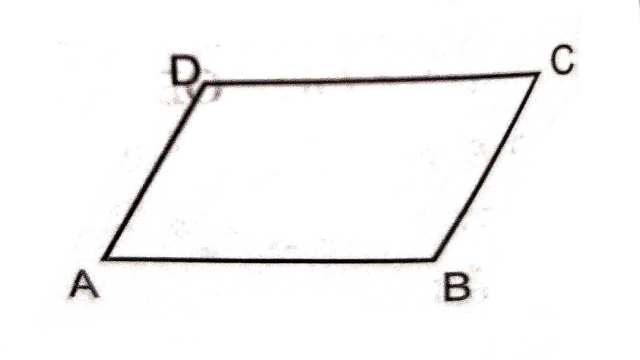
प्रमेय (Theorem):8.2.एक समान्तर चतुर्भुज में सम्मुख भुजाएँ बराबर होती है।
दिया है (Given):ABCD एक समान्तर चतुर्भुज है।
सिद्ध करना है (To Prove):AB=DC और AD=BC
रचना (Construction):समान्तर चतुर्भुज के विकर्ण AC को मिलाया।
उपपत्ति (Proof):![]() और
और ![]() में
में![]() (एकान्तर कोण)
(एकान्तर कोण)![]() (एकान्तर कोण)
(एकान्तर कोण)
AC=AC (उभयनिष्ठ भुजा है)
अतः ASA सर्वांगसमता गुणधर्म से
![]()
AB=DC और AD=BC (CPCT से)
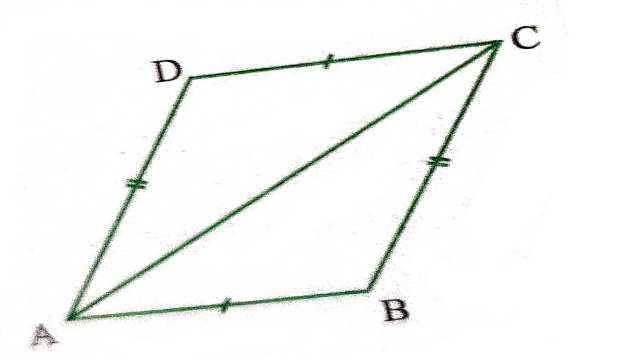
प्रमेय (Theorem):8.3.यदि एक चतुर्भुज की सम्मुख भुजाओं का प्रत्येक युग्म बराबर हो तो वह एक समान्तर चतुर्भुज होता है।
दिया है (Given:समान्तर चतुर्भुज ABCD में AB=CD और BC=AD
सिद्ध करना है (To Prove):ABCD एक समान्तर चतुर्भुज है अर्थात् ![]() व
व ![]()
रचना (Construction):विकर्ण AC को मिलाया।
उपपत्ति (Proof): ![]() और
और ![]() में
में
AB=CD (दिया है)
BC=AD (दिया है)
AC=AC (उभयनिष्ठ भुजा है)
SSS सर्वांगसमता गुणधर्म से![]() (CPCT से)
(CPCT से)![]() (CPCT से)
(CPCT से)
दो सरल रेखाओं को एक तिर्यक रेखा प्रतिच्छेद करती है और इस प्रकार बने एकान्तर कोण समान हों तो रेखाएँ समान्तर होती हैं।
![]()
ABCD एक समान्तर चतुर्भुज है।
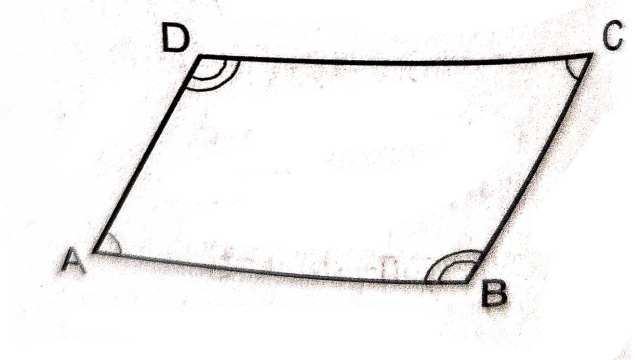
प्रमेय (Theorem):8.4.एक समान्तर चतुर्भुज के सम्मुख कोण बराबर होते हैं।
दिया है (Given):ABCD एक समान्तर चतुर्भुज है।
सिद्ध करना है (To Prove): ![]()
उपपत्ति (Proof):ABCD एक समान्तर चतुर्भुज है अतः![]() एवं
एवं ![]() है।
है।![]() (क्रमागत अन्तःकोण) … (1)
(क्रमागत अन्तःकोण) … (1)![]() (क्रमागत अन्तःकोण)….. (2)
(क्रमागत अन्तःकोण)….. (2)
(1) और (2) सेः
![]()
इसी प्रकार ![]()
प्रमेय (Theorem):8.5.यदि एक चतुर्भुज में सम्मुख कोणों का प्रत्येक युग्म बराबर हो तो वह एक समान्तर चतुर्भुज होता है।
दिया है (Given):चतुर्भुज ABCD में ![]()
सिद्ध करना है (To Prove):ABCD एक समान्तर चतुर्भुज है।
उपपत्ति (Proof):चतुर्भुज ABCD में दिया है![]() और
और ![]()
जोड़ने पर
![]()
(1) व (2) सेः
![]()
अर्थात् रेखा AB, रेखाओं AD और BC को क्रमशः A और B पर प्रतिच्छेद करती है जिससे![]() (तिर्यक रेखा के एक ही ओर के अन्तःकोण)
(तिर्यक रेखा के एक ही ओर के अन्तःकोण)
अतः ![]()
इसी प्रकार ![]()
अतः ![]()
(3) और (4) सेः![]() ABCD एक समान्तर चतुर्भुज है।
ABCD एक समान्तर चतुर्भुज है।
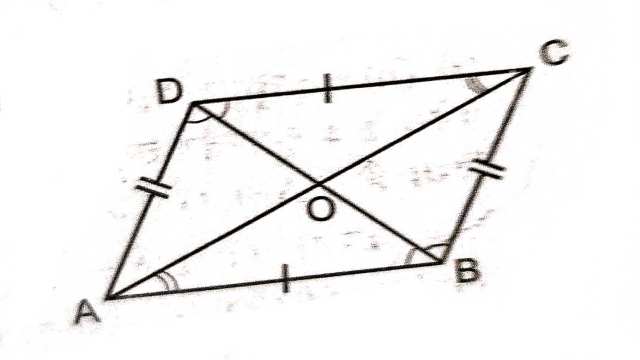
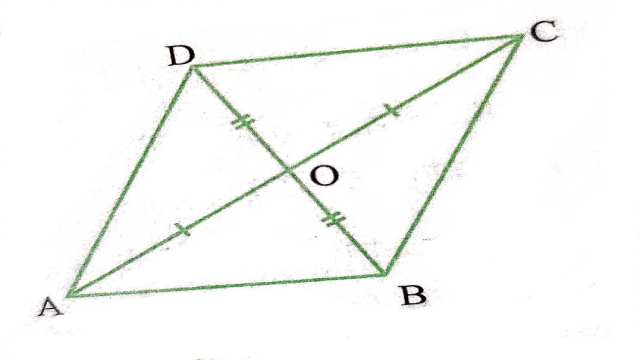
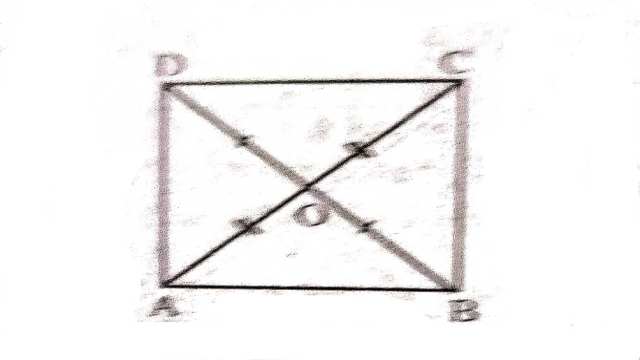
प्रमेय (Theorem):8.6.समान्तर चतुर्भुज के विकर्ण एक दूसरे को (परस्पर) समद्विभाजित करते हैं।
दिया है (Given):समान्तर चतुर्भुज ABCD के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं।
सिद्ध करना है (To Prove):AO=OC और OB=OD
उपपत्ति (Proof): ![]() एवं
एवं ![]() में
में![]() (एकान्तर कोण)
(एकान्तर कोण)
AD=BC (समान्तर चतुर्भुज की सम्मुख भुजाएँ)![]() (एकान्तर कोण)
(एकान्तर कोण)
अतः ASA सर्वांगसमता गुणधर्म से
![]()
OD=OB और OA=OC (CPCT से)
प्रमेय (Theorem):8.7.(प्रमेय 8.6 का विलोम):यदि एक चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करें, तो वह एक समान्तर चतुर्भुज होता है।
दिया है (Given):एक चतुर्भुज ABCD जिसके विकर्ण AC और BD बिन्दु D पर समद्विभाजित करते हैं अर्थात् OA=OC और OB=OD
सिद्ध करना है (To Prove):ABCD एक समान्तर चतुर्भुज है।
उपपत्ति (Proof): ![]() और
और ![]() में
में
OA=OC (दिया है)![]() (शीर्षाभिमुख कोण)
(शीर्षाभिमुख कोण)
OB=OD (दिया है)
अतः SAS सर्वांगसमता गुणधर्म से![]() (CPCT से)
(CPCT से)
परन्तु यह तिर्यक रेखा AC द्वारा रेखाओं AB और CD पर बने एकान्तर कोण हैं।अतः ![]()
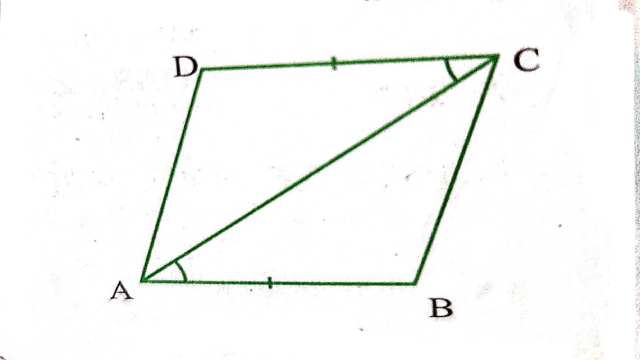
प्रमेय (Theorem):8.8.कोई चतुर्भुज एक समान्तर चतुर्भुज होता है,यदि उसकी सम्मुख भुजाओं का एक युग्म बराबर हो और समान्तर हो।
दिया है (Given):एक चतुर्भुज ABCD में ![]() और AB=DC है।
और AB=DC है।
सिद्ध करना है (To Prove):ABCD एक समान्तर चतुर्भुज है।
रचना (Construction):A को C से मिलाया।
उपपत्ति (Proof):और तिर्यक रेखा AC इनको प्रतिच्छेद करती है।
अतः ![]() (एकान्तर कोण)
(एकान्तर कोण)![]() और
और ![]() में
में
AB=DC (दिया है)![]() [(1) से]
[(1) से]
AC=AC (उभयनिष्ठ भुजा है)
SAS सर्वांगसमता गुणधर्म से
![]()
अतः ![]() (CPCT से)
(CPCT से)
अब AD,BC दो रेखाएँ हैं और तिर्यक रेखा AC इनको इस प्रकार प्रतिच्छेद करती है कि एकान्तर कोण ![]() एवं
एवं ![]() समान है।
समान है।
अतः ![]() (दिया है)
(दिया है)
अतः ABCD एक समान्तर चतुर्भुज है।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Inequalities of Triangle in Class 9
2.चतुर्भुज कक्षा 9 के साधित उदाहरण (Quadrilaterals Class 9 Solved Examples):
Example:1.एक चतुर्भुज के सभी कोण 3:5:9:13 के अनुपात में हैं।इस चतुर्भुज के सभी कोण ज्ञात कीजिए।
Solution:माना कि कोण 3x,5x,9x और 13x हैं।चतुर्भुज के कोणों का योग 360° होता है।अतः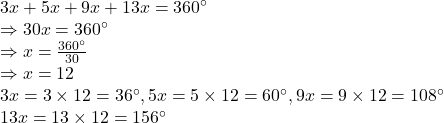
अतः चतुर्भुज के कोण हैंः36°,60°,108°,156°
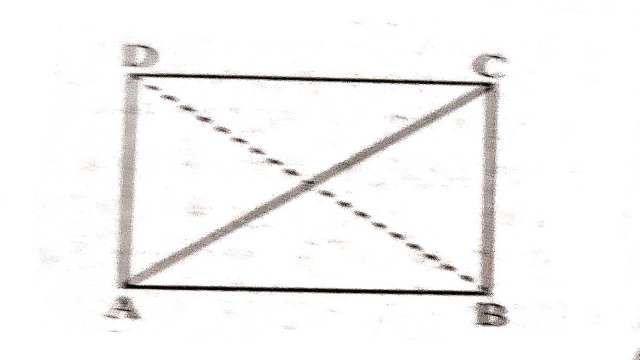
Example:2.यदि एक समान्तर चतुर्भुज के विकर्ण बराबर हों तो दर्शाइए कि वह एक आयत है।
Solution:दिया है (Given):समान्तर चतुर्भुज ABCD में विकर्ण AC=विकर्ण BD
सिद्ध करना है (To Prove):ABCD एक आयत है।
उपपत्ति (Proof):![]() और
और ![]() में
में
AC=BD (दिया है)
BC=BC (उभयनिष्ठ है)
AB=DC (समान्तर चतुर्भुज की सम्मुख भुजाएँ)
SSS सर्वांगसमता गुणधर्म से![]() (CPCT)
(CPCT)
परन्तु ![]()
(तिर्यक रेखा BC के एक ही ओर बने अन्तःकोण)
(1) व (2) सेः
![]()
अतः समान्तर चतुर्भुज ABCD एक आयत है।
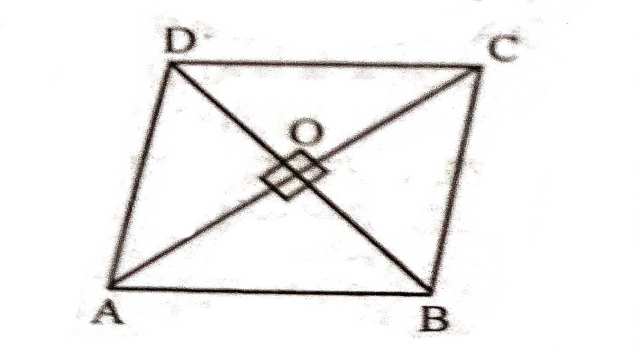
Example:3.दर्शाइए कि यदि एक चतुर्भुज के विकर्ण परस्पर समकोण पर समद्विभाजित करें,तो वह एक समचतुर्भुज होता है।
Solution:दिया है (Given):चतुर्भुज ABCD के विकर्ण AC और BD एक दूसरे को समकोण पर समद्विभाजित करते हैं।अतः
![]()
सिद्ध करना है (To Prove):चतुर्भुज ABCD एक समचतुर्भुज है।
उपपत्ति (Proof):![]() और
और ![]() में
में
OD=OB (दिया है)![]() (दिया है)
(दिया है)
OA=OA (उभयनिष्ठ भुजा है)
अतः SAS सर्वांगसमता गुणधर्म से
![]()
AB=AD (CPCT)
इसी प्रकार AB=BC=CD
अतःAB=BC=CD=AD
फलतः ABCD एक समचतुर्भुज है।
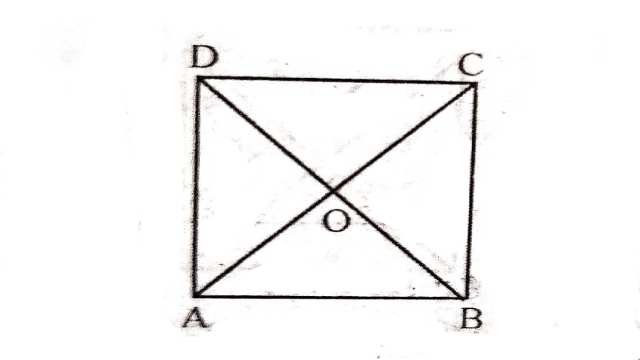
Example:4.दर्शाइए कि एक वर्ग के विकर्ण बराबर होते हैं और परस्पर समकोण पर समद्विभाजित करते हैं।
Solution:दिया है (Given):ABCD एक वर्ग है।
सिद्ध करना है (To Prove):(i)AC=BD
(ii)AC और BD परस्पर समकोण पर समद्विभाजित करते हैं।
उपपत्ति (Proof):(i)![]() और
और ![]() में
में
AB=AB (उभयनिष्ठ भुजा है)
BC=AD (वर्ग की भुजाएँ)![]() (वर्ग का प्रत्येक कोण 90° होता है)
(वर्ग का प्रत्येक कोण 90° होता है)
SAS सर्वांगसमता गुणधर्म से
![]()
AB=BD (CPCT से)
(ii)![]() और
और ![]() में
में
AD=BC (वर्ग की भुजाएँ)![]() (एकान्तर कोण)
(एकान्तर कोण)![]() (एकान्तर कोण)
(एकान्तर कोण)
ASA सर्वांगसमता गुणधर्म से
![]()
OA=OC (CPCT)… (1)
इसी प्रकार सिद्ध कर सकते हैं कि
OB=OD …. (2)
समीकरण (1) और (2) सेः
AC और BD परस्पर समद्विभाजित करते हैं।![]() और
और ![]() में
में
OB=OD [समी.(2) से]
BA=DA (वर्ग की भुजाएँ)
OA=OA (उभयनिष्ठ भुजा है)
SSS सर्वांगसमता गुणधर्म से![]() (CPCT से)
(CPCT से)
![]() (रैखिक कोण युग्म अभीगृहीत से)
(रैखिक कोण युग्म अभीगृहीत से)
![]()
अतः AC और BD परस्पर समकोण पर समद्विभाजित करते हैं।
Example:5.दर्शाइए कि यदि एक चतुर्भुज के विकर्ण बराबर हों और परस्पर लम्बवत समद्विभाजित करें तो वह एक वर्ग होता है।
Solution:दिया है (Given):चतुर्भुज ABCD के विकर्ण AC और BD बराबर हैं और परस्पर लम्बवत समद्विभाजित करते हैं।
सिद्ध करना है ( To Prove):चतुर्भुज ABCD एक वर्ग है।
उपपत्ति (Proof): ![]() और
और ![]() में
में
OA=OC (दिया है)
OD=OB (दिया है)![]() (शीर्षाभिमुख कोण)
(शीर्षाभिमुख कोण)
SAS सर्वांगसमता गुणधर्म सेः
![]()
AB=CB (CPCT)![]() (CPCT)
(CPCT)
![]()
अब AD=CB और ![]()
इसलिए चतुर्भुज ABCD एक समान्तर चतुर्भुज है।![]() और
और ![]() में
में
OB=OD (दिया है)![]() (दिया है)
(दिया है)
SAS सर्वांगसमता गुणधर्म से
![]()
AB=AD![]() ABCD एक समान्तर चतुर्भुज है और AB=AD
ABCD एक समान्तर चतुर्भुज है और AB=AD![]() ABCD एक समचतुर्भुज है।
ABCD एक समचतुर्भुज है।![]() और
और ![]() में
में
AC=BD (दिया है)
AB=AB (उभयनिष्ठ भुजा है)
BC=AD (ABCD समचतुर्भुज है)
SSS सर्वांगसमता गुणधर्म से![]() (CPCT)
(CPCT)
![]()
(समान्तर चतुर्भुज ABCD की सम्मुख भुजाएँ)
और तिर्यक रेखा AB इन्हें काटती है,![]() (तिर्यक रेखा के एक ही ओर के अन्तःकोणों का योग 180° होता है)
(तिर्यक रेखा के एक ही ओर के अन्तःकोणों का योग 180° होता है)
![]()
इसी प्रकार ![]()
इसलिए ABCD एक वर्ग है।
Example:6.समान्तर चतुर्भुज ABCD का विकर्ण AC कोण A को समद्विभाजित करता है (देखिए आकृति)।दर्शाइए कि
(i)यह को भी समद्विभाजित करता है।
(ii) ABCD एक समचतुर्भुज है।
Solution:दिया है (Given):समान्तर चतुर्भुज ABCD का विकर्ण AC, ![]() को समद्विभाजित करता है।
को समद्विभाजित करता है।
सिद्ध करना है (To Prove):(i)यह ![]() को समद्विभाजित करता है।
को समद्विभाजित करता है।
(ii)ABCD एक समचतुर्भुज है।
उपपत्ति (Proof):(i) ![]() और
और ![]() में
में
AD=BC (समान्तर चतुर्भुज की सम्मुख भुजाएँ)
AB=DC (समान्तर चतुर्भुज की सम्मुख भुजाएँ)
AC=AC (उभयनिष्ठ भुजा है)
SSS सर्वांगसमता गुणधर्म से
![]() (CPCT)
(CPCT)![]() (CPCT)
(CPCT)
अतः ![]() (
(![]() दिया है)
दिया है)
अतः AC, ![]() को समद्विभाजित करता है।
को समद्विभाजित करता है।
(ii) ![]()
AD=CD (बराबर भुजाओं के सम्मुख कोण)
AB=CD=AD=BC
अतः ABCD एक समचतुर्भुज है।
Example:7.ABCD एक समचतुर्भुज है।दर्शाइए कि विकर्ण AC कोणों A और C दोनों को समद्विभाजित करता है तथा विकर्ण BD कोणों B,D दोनों को समद्विभाजित करता है।
Solution:दिया है (Given):एक समचतुर्भुज ABCD
सिद्ध करना है (To Prove):(i) ![]()
(ii) ![]()
(iii)![]()
(iv) ![]()
उपपत्ति (Proof):![]() में
में
AD=CD![]() (बराबर भुजा के सम्मुख कोण)
(बराबर भुजा के सम्मुख कोण)![]() (एकान्तर कोण)
(एकान्तर कोण)
इसलिए ![]()
अतः AC, ![]() को समद्विभाजित करता है।
को समद्विभाजित करता है।
इसी प्रकार हम सिद्ध कर सकते हैं कि AC, ![]() और
और ![]() को और BD,
को और BD, ![]() और
और ![]() को समद्विभाजित करते हैं।
को समद्विभाजित करते हैं।
Example:8.ABCD एक आयत है जिसमें विकर्ण AC दोनों कोणों A और C को समद्विभाजित करता है दर्शाइए कि (i)ABCD एक वर्ग है (ii)विकर्ण BD दोनों कोणों B और D को समद्विभाजित करता है।
Solution:दिया है (Given):आयत ABCD में AC, ![]() को तथा
को तथा ![]() को समद्विभाजित करता है।
को समद्विभाजित करता है।
सिद्ध करना है (To Prove):(i)ABCD एक वर्ग है।
(ii)विकर्ण BD, ![]() तथा
तथा ![]() को समद्विभाजित करता है।
को समद्विभाजित करता है।
उपपत्ति (Proof):(i)![]() में
में
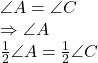
अतः ![]()
AD=CD (बराबर कोणों की सम्मुख भुजाएँ)
अतः ABCD एक समचतुर्भुज है और यह दिया गया है कि यह एक आयत है।
अतः ABCD एक वर्ग है।
(ii)एक वर्ग में ,विकर्ण परस्पर समद्विभाजित होते हैं।अतः विकर्ण BD, ![]() तथा
तथा ![]() को समद्विभाजित करता है।
को समद्विभाजित करता है।
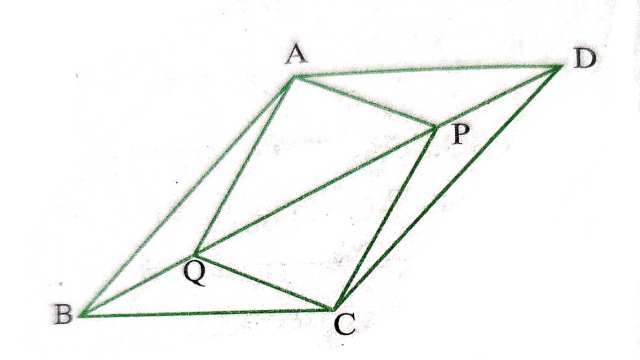
Example:9.समान्तर चतुर्भुज ABCD के विकर्ण BD पर दो बिन्दु P और Q इस प्रकार स्थित हैं कि DP=BQ है (देखिए आकृति)।दर्शाइए कि
(i)![]()
(ii)AP=CQ
(iii)![]()
(iv)AQ=CP
(v)APCQ एक समान्तर चतुर्भुज है।
Solution:दिया है (Given):समान्तर चतुर्भुज के विकर्ण BD पर दो बिन्दु P और Q इस प्रकार स्थित हैं कि DP=BQ है।
सिद्ध करना है (To Prove)(i) ![]()
(ii)AP=CQ
(iii)![]()
(iv)AQ=CP
(v)APCQ एक समान्तर चतुर्भुज है।
उपपत्ति (Proof)(i) ![]() और
और ![]() में
में
AD=BC (समान्तर चतुर्भुज ABCD की सम्मुख भुजाएँ)
PD=BQ (दिया है)![]() (एकान्तर कोण)
(एकान्तर कोण)
अतः SAS सर्वांगसमता गुणधर्म से
![]()
(ii)![]() (सिद्ध किया है)
(सिद्ध किया है)
AP=CQ (CPCT)
(iii)![]() तथा
तथा ![]() में
में
AB=CD (समान्तर चतुर्भुज की सम्मुख भुजाएँ)![]() (एकान्तर कोण)
(एकान्तर कोण)
BQ=PD (दिया है)
SAS सर्वांगसमता गुणधर्म से
![]()
(iv)![]() (सिद्ध किया है)
(सिद्ध किया है)
AQ=CP (CPCT से)
(v)AP=CQ तथा AQ=CP (सिद्ध किया है)
अतः APCQ समान्तर चतुर्भुज है।
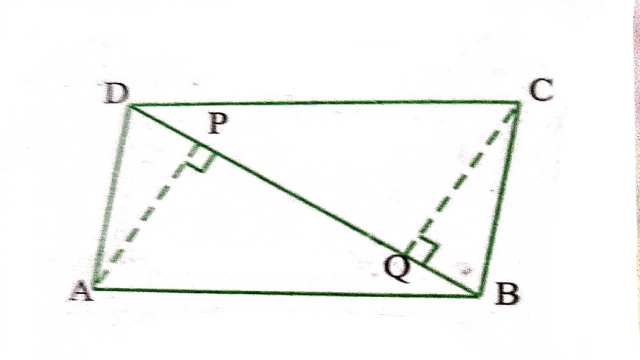
Example:10.ABCD एक समान्तर चतुर्भुज है तथा AP=CQ शीर्षों A और C से विकर्ण BD पर क्रमशः लम्ब हैं (देखिए आकृति)।दर्शाइए कि
(i)![]()
(ii)AP=CQ
Solution:दिया है (Given):ABCD एक समान्तर चतुर्भुज है तथा AP और CQ शीर्षों A और C से विकर्ण BD पर क्रमशः लम्ब हैं।
सिद्ध करना है (To Prove):(i) ![]()
(ii)AP=CQ
उपपत्ति (Proof):(i)![]() और
और ![]() में
में
AB=CD (समान्तर चतुर्भुज की सम्मुख भुजाएँ)![]() (एकान्तर कोण)
(एकान्तर कोण)![]() (दिया है)
(दिया है)
AAS सर्वांगसमता गुणधर्म से
![]()
(ii)![]() (सिद्ध किया है)
(सिद्ध किया है)
AP=CQ (CPCT)
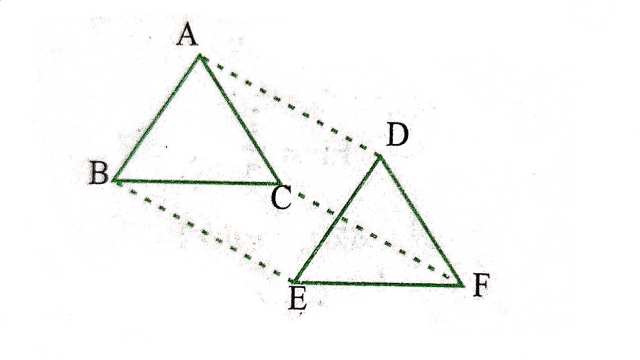
Example:11. ![]() और
और ![]() में, AB=DE,
में, AB=DE,![]() ,BC=EF और
,BC=EF और ![]() है।शीर्षों A,B और C को क्रमशः शीर्षों D,E और F से जोड़ा जाता है (देखिए आकृति)।दर्शाइए कि
है।शीर्षों A,B और C को क्रमशः शीर्षों D,E और F से जोड़ा जाता है (देखिए आकृति)।दर्शाइए कि
(i)चतुर्भुज ABED एक समान्तर चतुर्भुज है।
(ii)चतुर्भुज BEFC एक समान्तर चतुर्भुज है।
(iii)![]() और AD=CF है।
और AD=CF है।
(iv)चतुर्भुज ACFD एक समान्तर चतुर्भुज है।
(v)AC=DF है।
(vi)![]() है।
है।
Solution:दिया है (Given): ![]() और
और ![]() में A B=D E,
में A B=D E,![]() , BC=EF,
, BC=EF,![]() है।शीर्षों A,B और C को क्रमशः शीर्षों D,E और F से जोड़ा जाता है।
है।शीर्षों A,B और C को क्रमशः शीर्षों D,E और F से जोड़ा जाता है।
सिद्ध करना है (To Prove):(i)चतुर्भुज ABED एक समान्तर चतुर्भुज है।
(ii)चतुर्भुज BEFC एक समान्तर चतुर्भुज है।
(iii)![]() और AD=CF है।
और AD=CF है।
(iv)चतुर्भुज ACFD एक समान्तर चतुर्भुज है।
(v)AC=DF है।
(vi)![]() है।
है।
उपपत्ति (Proof):(i)चतुर्भुज ABED में![]() और AB=DE
और AB=DE
अतः ABED एक समान्तर चतुर्भुज है।
(ii)चतुर्भुज BECF में,
BC=EF और ![]() (दिया है)
(दिया है)
BECF एक समान्तर चतुर्भुज है।
अतः ![]() और BE=CF
और BE=CF
(iii)अब ![]() , AD=BE
, AD=BE
और ![]() , BE=CF
, BE=CF
(समान्तर चतुर्भुज की सम्मुख भुजाएँ)
इसलिए ![]() और AD=CF
और AD=CF
(iv)चतुर्भुज ACFD में ![]() व AD=CF
व AD=CF
अतः ACFD एक समान्तर चतुर्भुज है।
(v)चूँकि ACFD एक समान्तर चतुर्भुज है।![]() AC=DF और
AC=DF और ![]()
(vi) ![]() और
और ![]() में
में
AB=DE (दिया है)
BC=EF (दिया है)
AC=DF (सिद्ध किया है)
SSS सर्वांगसमता गुणधर्म से
![]()
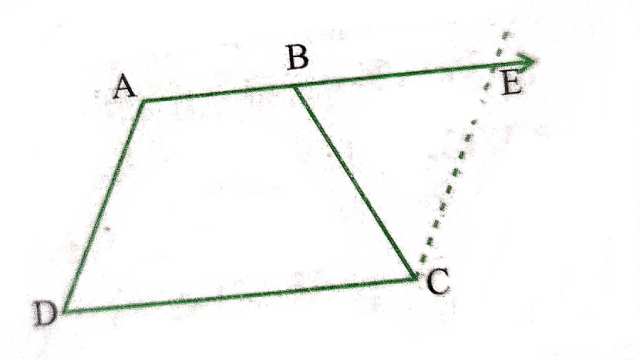
Example:12.ABCD एक समलम्ब है जिसमें ![]() और AD=BC (देखिए आकृति)।
और AD=BC (देखिए आकृति)।
दर्शाइए कि
(i)![]()
(ii)![]()
(iii)![]()
(iv)विकर्ण AC=विकर्ण BD
Solution:दिया है (Given):ABCD एक समलम्ब चतुर्भुज है जिसमें ![]() और AD=BC
और AD=BC
सिद्ध करना है (To Prove):(i)![]()
(ii)![]()
(iii)![]()
(iv)विकर्ण AC=विकर्ण BD
रचना (Construction):AB को बढ़ाया और C से होकर DA के समान्तर एक रेखा खींची जो बढ़ी हुई भुजा AB को E पर प्रतिच्छेद करे।
उपपत्ति (Proof):(i)चतुर्भुज ADCE में![]() (रचना से)
(रचना से)![]() (दिया है)
(दिया है)
इसलिए ADCE एक समान्तर चतुर्भुज है।
अब AD=EC और AD=BC
EC=BC
इस प्रकार ![]()
(त्रिभुज की समान भुजाओं के सम्मुख कोण)![]() (तिर्यक रेखा के एक ही ओर बने कोणों का योग)
(तिर्यक रेखा के एक ही ओर बने कोणों का योग)
![]()
परन्तु ![]() (रैखिक कोण युग्म)
(रैखिक कोण युग्म)
![]()
अतः ![]()
(ii) ![]() और
और ![]() [ABCD समलम्ब है]
[ABCD समलम्ब है]
(iii)![]() और
और ![]() में
में
BC=AD (दिया है)
AB=AB (उभयनिष्ठ भुजा है)![]() (सिद्ध किया है)
(सिद्ध किया है)
SAS सर्वांगसमता गुणधर्म से
![]()
(iv)विकर्ण AC=विकर्ण BD (CPCT)
उपर्युक्त उदाहरणों के द्वारा चतुर्भुज कक्षा 9 (Quadrilaterals Class 9),कक्षा 9 में चतुर्भुज (Quadrilaterals in Class 9) को समझ सकते हैं।
3.चतुर्भुज कक्षा 9 के सवाल (Quadrilaterals Class 9 Questions):
(1.)ABCD एक समलम्ब है जिसमें ![]() और
और ![]() है।इस समलम्ब के कोण C और D ज्ञात कीजिए।
है।इस समलम्ब के कोण C और D ज्ञात कीजिए।
(2.)एक समान्तर चतुर्भुज के एक अधिक कोण के शीर्ष से खींचे गए उस समान्तर चतुर्भुज के शीर्षलम्बों के बीच का कोण 60° है।इस समान्तर चतुर्भुज के सभी कोण ज्ञात कीजिए।
उत्तर (Answers):(1.)प्रत्येक 135°
(2.)60°,120°,60°,120°
उपर्युक्त सवालों को हल करने पर चतुर्भुज कक्षा 9 (Quadrilaterals Class 9),कक्षा 9 में चतुर्भुज (Quadrilaterals in Class 9) को ठीक से समझ सकते हैं।
Also Read This Article:-Triangle in Class 9
4.चतुर्भुज कक्षा 9 (Frequently Asked Questions Related to Quadrilaterals Class 9),कक्षा 9 में चतुर्भुज (Quadrilaterals in Class 9) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.समलम्ब चतुर्भुज किसे कहते हैं? (What is a Trapezium?):
उत्तर:यदि किसी चतुर्भुज ABCD की सम्मुख भुजाओं AB और CD का एक युग्म समान्तर है तो यह एक समलम्ब चतुर्भुज है।
प्रश्न:2.समान्तर चतुर्भुज किसे कहते हैं? (What is a Parallelogram?):
उत्तर:यदि किसी चतुर्भुज में सम्मुख भुजाओं के दोनों युग्म समान्तर हों तो यह समान्तर चतुर्भुज कहलाता है।
प्रश्न:3.आयत किसे कहते हैं? (What is a Rectangle?):
उत्तर:समान्तर चतुर्भुज का प्रत्येक कोण 90° हो तो यह आयत (Ractangle) कहलाता है।
उपर्युक्त प्रश्नों के उत्तर द्वारा चतुर्भुज कक्षा 9 (Quadrilaterals Class 9),कक्षा 9 में चतुर्भुज (Quadrilaterals in Class 9) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Quadrilaterals Class 9
चतुर्भुज कक्षा 9 (Quadrilaterals Class 9)
Quadrilaterals Class 9
चतुर्भुज कक्षा 9 (Quadrilaterals Class 9) में चतुर्भुज वह आकृति है जो चारों बिन्दुओं को एक
क्रम में जोड़ने से प्राप्त होती है।आप अपने परिवेश (चारों ओर) में, अपने आसपास चतुर्भुज
के आकार की अनेक वस्तुएँ देख सकते हैं
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.