1.समाकल में क्षेत्रकलन विधि (Quadrature Method in Integrals),ध्रुवीय समीकरणों वाले वक्रों तथा ध्रुवान्तर रेखाओं से परिबद्ध क्षेत्रफल (Area Bounded by Curves in Polar Equations and Radii Vectors):

• समाकल में क्षेत्रकलन विधि (Quadrature Method in Integrals) के इस आर्टिकल में दो वक्रों का उभयनिष्ठ क्षेत्रफल तथा द्वि-समाकलन से ध्रुवीय वक्रों से परिबद्ध क्षेत्रफल ज्ञात करने का अध्ययन करेंगे।
  आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:SA of Solids of Revolution

2.समाकल में क्षेत्रकलन विधि के साधित उदाहरण (Quadrature Method in Integrals Solved Examples):

Example:1.निम्नलिखित वक्रों तथा उनके अनन्तस्पर्शी के बीच का क्षेत्रफल ज्ञात कीजिए:
(Find the area between the following curves and their asymptotes):
(a):r=a\left(\sec{\theta}+\cos{\theta}\right)

Solution:r=a\left(\sec{\theta}+\cos{\theta}\right)
r=a\left(\frac{1}{\cos{\theta}}+\cos{\theta}\right)
\Rightarrow{r\cos{\theta}}=a\left(1+\cos^{2}{\theta}\right)
x=r\cos{\theta},y=r\sin{\theta}\text{ तथा }r^{2}=x^{2}+y^{2}
उपर्युक्त मान रखकर कार्तीय निर्देशांकों में परिवर्तित करने पर:
x=a\left(1+\frac{x^{2}}{r^{2}}\right)
\Rightarrow{x}=a\left(1+\frac{x^{2}}{x^{2}+y^{2}}\right)
\Rightarrow{x\left(x^{2}+y^{2}\right)}=a\left(2x^{2}+y^{2}\right)
\Rightarrow{x^{3}+xy^{2}}=2ax^{2}+ay^{2}
\Rightarrow{xy^{2}-ay^{2}}=2ax^{2}-x^{3}
\Rightarrow{y^{2}\left(x-a\right)}=x^{2}\left(2a-x\right)
\Rightarrow{y^{2}}=\frac{\left(2a-x\right)x^{2}}{x-a}
\Rightarrow{y}=\sqrt{\frac{2a-x}{x-a}}x
अनन्तस्पर्शी x-a तथा x-2a है अतः अभीष्ट क्षेत्रफल=2\int_{a}^{2a}ydx
=2\int_{a}^{2a}\sqrt{\frac{2a-x}{x-a}} xdx
\text{Put }x=a+a\sin^{2}{\theta}
dx=2a\sin{\theta}\cos{\theta}
\text{जब } x=a \text{ तो } y=0
\text{जब } x=2a \text{ तो }y=\frac{\pi}{2}
=2\int_{0}^{\frac{\pi}{2}}\sqrt{\frac{2a-a-a\sin^{2}{\theta}}{a+a\sin^{2}{\theta}-a}}\left(a+a\sin^{2}{\theta}\right)\left(2a\sin{\theta}\cos{\theta}\right){d\theta}
=4a^{2}\int_{0}^{\frac{\pi}{2}}\left(\frac{\cos{\theta}}{\sin{\theta}}\right)\left(1+\sin^{2}{\theta}\right)\left(\sin{\theta}\cos{\theta}\right){d\theta}
=4a^{2}\int_{0}^{\frac{\pi}{2}}\left(\cos^{2}{\theta}+\sin^{2}{\theta}\cos^{2}{\theta}\right){d\theta}
=4a^{2}\left[\frac{\Gamma{\left(\frac{2+1}{2}\right)}\Gamma{\left(\frac{1}{2}\right)}}{2\Gamma{\left(\frac{2+0+2}{2}\right)}}+\frac{\Gamma{\left(\frac{2+1}{2}\right)}\Gamma{\left(\frac{2+1}{2}\right)}}{2\Gamma{\left(\frac{2+2+2}{2}\right)}}\right]
=2a^{2}\left[\frac{1}{2}\sqrt{\pi}\sqrt{\pi}+\frac{\frac{1}{2}.\sqrt{\pi}\frac{1}{2}.\sqrt{\pi}}{2}\right]
=2a^{2}\left[\frac{\pi}{2}+\frac{\pi}{8}\right]
=2a^{2}\left[\frac{{4\pi}+{\pi}}{8}\right]
=\frac{5}{4}{\pi}a^{2}
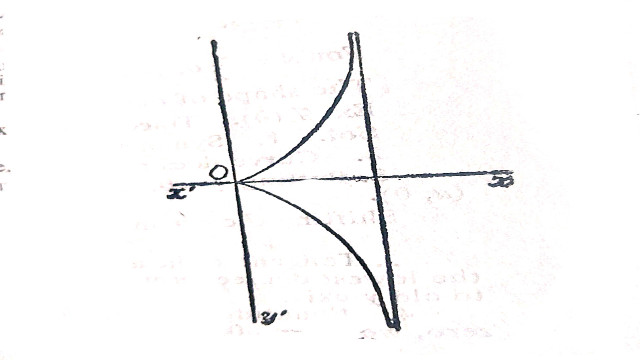
(b):r=\frac{a\sin^{2}{\theta}}{\cos{\theta}} [cissiod]

Solution:r=\frac{a\sin^{2}{\theta}}{\cos{\theta}}
\Rightarrow{r\cos{\theta}}=a\sin^{2}{\theta}
कार्तीय निर्देशांकों में परिवर्तित करने पर:
x=a\frac{y^{2}}{x^{2}}
\Rightarrow{x}=a\frac{y^{2}}{x^{2}+y^{2}}
\Rightarrow{x^{3}+xy^{2}}=ay^{2}
\Rightarrow{ay^{2}-xy^{2}}=x^{3}
\Rightarrow{y^{2}\left(a-x\right)}=x^{3}
\Rightarrow{y}=x\sqrt{\frac{x}{a-x}}
अभीष्ट क्षेत्रफल=2\int_{0}^{a} ydx
=2\int_{0}^{a}x\sqrt{\frac{x}{a-x}} dx
\text{Put }x=a\sin^{2}{\theta}
dx=2a\sin{\theta}\cos{\theta}{d\theta}
\text{जब } x=0 \text{ तो }{\theta}=0
\text{जब } x=a \text{ तो }{\theta}=\frac{\pi}{2}
=2\int_{0}^{\frac{\pi}{2}}a\sin^{2}{\theta}\sqrt{\frac{a\sin^{2}{\theta}}{a-a\sin^{2}{\theta}}}\left(2a\sin{\theta}\cos{\theta}{d\theta}\right)
=4a^{2}\int_{0}^{\frac{\pi}{2}}\sin^{2}{\theta}\left(\frac{\sin{\theta}}{\cos{\theta}}\right)\left(\sin{\theta}\cos{\theta}\right){d\theta}
=4a^{2}\int_{0}^{\frac{\pi}{2}}\sin^{4}{\theta}{d\theta}
4a^{2}\frac{\Gamma{\left(\frac{4+1}{2}\right)}\Gamma{\left(\frac{1}{2}\right)}}{2\Gamma{\left(\frac{4+0+2}{2}\right)}}
=2a^{2}\frac{\frac{3}{2}.\frac{1}{2}\sqrt{\pi}\frac{1}{2}.\sqrt{\pi}}{2×1}
=a^{2} × \frac{3{\pi}}{4}
=\frac{3}{4}{\pi}a^{2}
Example:2.सिद्ध कीजिए कि लिमेकन r=a+b\cos{\theta},a<b के दो लूपों के क्षेत्रफल का योगफल \frac{1}{2}{\pi}\left(2a^{2}+b^{2}\right) है।
(Prove that the sum of the areas of the two loops of the limacon r=a+b\cos{\theta},a<b is \frac{1}{2}{\pi}\left(2a^{2}+b^{2}\right).)

Solution:r=a+b\cos{\theta}
\text{माना }{\theta}={\alpha}
\text{जब }r=0 \text{ तब }r=a+b\cos{\alpha}=0
\cos{\alpha}=-\frac{a}{b} और रेखा {\theta}={\alpha} ध्रुव पर स्पर्श रेखा है।
बड़ा लूप का कोण {\theta},0 से {\alpha} तक बदलता है जबकि छोटे लूप का कोण {\alpha} से {\pi} तक बदलता है (प्रारम्भिक रेखा से ऊपर)
अभीष्ट क्षेत्रफल=2×\frac{1}{2}\int_{0}^{\alpha}r^{2}{d\theta}+2×\frac{1}{2}\int_{\alpha}^{\pi}r^{2}{d\theta}
\int_{0}^{\alpha}r^{2}{d\theta}+\int_{\alpha}^{\pi}r^{2}{d\theta}
=\int_{0}^{\pi}r^{2}{d\theta}
=\int_{0}^{\pi}\left(a+b\cos{\theta}\right)^{2}{d\theta}
=\int_{0}^{\pi}\left(a^{2}+2ab\cos{\theta}+b^{2}\cos^{2}{\theta}\right){d\theta}
=a^{2}\int_{0}^{\pi}{d\theta}+2ab\int_{0}^{\pi}\cos{\theta}{d\theta}+b^{2}\int_{0}^{\pi}\cos^{2}{\theta}{d\theta}
=a^{2}\left[{\theta}\right]_{0}^{\pi}+2ab\left[\sin{\theta}\right]_{0}^{\pi}+2b^{2}\int_{0}^{\frac{\pi}{2}}\cos^{2}{\theta}{d\theta}

={\pi}a^{2}+2b^{2}\frac{\Gamma{\left(\frac{2+1}{2}\right)}\Gamma{\left(\frac{1}{2}\right)}}{2\Gamma{\left(\frac{2+0+2}{2}\right)}}
={\pi}a^{2}+b^{2}\frac{1}{2}\sqrt{\pi}\sqrt{\pi}
={\pi}a^{2}+\frac{1}{2}{\pi}b^{2}
=\frac{1}{2}{\pi}\left(2a^{2}+b^{2}\right)
Example:3.सिद्ध कीजिए कि वक्र r=\frac{1}{2}+\cos{2\theta} के बड़े लूप व छोटे लूप के क्षेत्रफल का अनुपात \left(4{\pi}+3\sqrt{3}\right):\left(2{\pi}-3\sqrt{3}\right) है।
(Prove that the ratio of the area of the larger to the smaller loop of the curve r=\frac{1}{2}+\cos{2\theta} is \left(4{\pi}+3\sqrt{3}\right):\left(2{\pi}-3\sqrt{3}\right).)

Solution:r=\frac{1}{2}+\cos{2\theta}
r=0 से \cos{2\theta}=-\frac{1}{2}
\Rightarrow{2\theta}=\frac{2{\pi}}{3},\frac{4{\pi}}{3}
\Rightarrow{\theta}=\frac{\pi}{3},\frac{2{\pi}}{3}
रेखा \frac{\pi}{3} तथा \frac{2{\pi}}{3} वक्र की स्पर्श रेखाएँ है।
बड़ा लूप का कोण {\theta},-\frac{\pi}{3} से \frac{\pi}{3} तक परिवर्तित होता है जबकि छोटे लूप का कोण {\theta},\frac{\pi}{3} से \frac{2\pi}{3} तक परिवर्तित होता है।
बड़े लूप का क्षेत्रफल=2×\frac{1}{2}\int_{0}^{\frac{\pi}{3}}r^{2}{d\theta}
=\int_{0}^{\frac{\pi}{3}}\left(\frac{1}{2}+\cos{2\theta}\right)^{2}{d\theta}
=\int_{0}^{\frac{\pi}{3}}\left(\frac{1}{4}+\cos{2\theta}+\cos^{2}{2\theta}\right){d\theta}
=\int_{0}^{\frac{\pi}{3}}\left[\frac{1}{4}+\cos{2\theta}+\left(\frac{1+\cos{4\theta}}{2}\right)\right]{d\theta}
=\int_{0}^{\frac{\pi}{3}}\left(\frac{3}{4}+\cos{2\theta}+\frac{1}{2}\cos{4\theta}\right){d\theta}

=\left[\frac{3}{4}{\theta}\right]_{0}^{\frac{\pi}{3}}+\frac{1}{2}\left[\sin{2\theta}\right]_{0}^{\frac{\pi}{3}}+\frac{1}{8}\left[\sin{4\theta}\right]_{0}^{\frac{\pi}{3}}

=\frac{3}{4}.\frac{\pi}{3}+\frac{1}{2}.\frac{\sqrt{3}}{2}+\frac{1}{8}.\left(-\frac{\sqrt{3}}{2}\right) =\frac{\pi}{4}+\frac{\sqrt{3}}{4}-\frac{\sqrt{3}}{16}

=\frac{\pi}{4}+\frac{3\sqrt{3}}{16}

=\frac{1}{16}\left(4{\pi}+3\sqrt{3}\right)

छोटे लूप का क्षेत्रफल=

=\frac{1}{2}\int_{\frac{\pi}{3}}^{\frac{2\pi}{3}}r^{2}{d\theta}

=\frac{1}{2}\int_{\frac{\pi}{3}}^{\frac{2\pi}{3}}\left(\frac{1}{2}+\cos{2\theta}\right)^{2}{d\theta}
=\frac{1}{2}\int_{\frac{\pi}{3}}^{\frac{2\pi}{3}}\left(\frac{1}{4}+\cos{2\theta}+\cos^{2}{2\theta}\right){d\theta}
=\frac{1}{2}\int_{\frac{\pi}{3}}^{\frac{2\pi}{3}}\left[\frac{1}{4}+\cos{2\theta}+\left(\frac{1+\cos{4\theta}}{2}\right)\right]{d\theta}
=\frac{1}{2}\int_{\frac{\pi}{3}}^{\frac{2\pi}{3}}\left(\frac{3}{4}+\cos{2\theta}+\frac{1}{2}\cos{4\theta}\right){d\theta}

=\frac{1}{2}\left[\frac{3}{4}{\theta}\right]_{\frac{\pi}{3}}^{\frac{2\pi}{3}}+\frac{1}{4}\left[\sin{2\theta}\right]_{\frac{\pi}{3}}^{\frac{2\pi}{3}}+\frac{1}{16}\left[\sin{4\theta}\right]_{\frac{\pi}{3}}^{\frac{2\pi}{3}}

=\frac{\pi}{4}-\frac{\pi}{8}+\frac{1}{4}\left(-\frac{\sqrt{3}}{2}-\frac{\sqrt{3}}{2}\right)+\frac{1}{16}.\left(\frac{\sqrt{3}}{2}+\frac{\sqrt{3}}{2}\right)

=\frac{\pi}{8}-\frac{\sqrt{3}}{4}+\frac{\sqrt{3}}{16} =\frac{\pi}{8}-\frac{3\sqrt{3}}{16}

=\frac{1}{16}\left(2{\pi}-3\sqrt{3}\right)

अभीष्ट अनुपात=\frac{\text{बड़े लूप का क्षेत्रफल}}{\text{छोटे लूप का क्षेत्रफल}} =\frac{\left(\frac{1}{16}\right)\left(4{\pi}+3\sqrt{3}\right)}{\left(\frac{1}{16}\right)\left(2{\pi}-3\sqrt{3}\right)} =\left(4{\pi}+3\sqrt{3}\right):\left(2{\pi}-3\sqrt{3}\right)

Example:4.निम्नलिखित वक्रों का उभयनिष्ठ क्षेत्रफल ज्ञात कीजिए: (Find the area common to the following curves):

(a):r=a,r=a\left(1+\cos{\theta}\right)

Solution:r=a,r=a\left(1+\cos{\theta}\right)

प्रतिच्छेद बिन्दु a=a\left(1+\cos{\theta}\right)

\Rightarrow{\cos{\theta}}=0

\Rightarrow{\theta}=\frac{\pi}{2}

अत: दोनों वक्र \frac{\pi}{2} पर मिलते हैं।

उभयनिष्ठ क्षेत्रफल=\frac{1}{2}{\int}r^{2}{d\theta}\text{ वृत्त से }+\frac{1}{2}{\int}r^{2}{d\theta}\text{ कार्डिआइड से }

=2×\frac{1}{2}\int_{0}^{\frac{\pi}{2}}a^{2}{d\theta}+2×\frac{1}{2}\int_{\frac{\pi}{2}}^{\pi}a^{2}\left(1+\cos{\theta}\right)^{2}{d\theta}
=a^{2}\left[{\theta}\right]{0}^{\frac{\pi}{2}}+a^{2}\int{\frac{\pi}{2}}^{\pi}\left(1+2\cos{\theta}+\cos^{2}{\theta}\right){d\theta}

=\frac{{\pi}a^{2}}{2}+a^{2}\int_{\frac{\pi}{2}}^{\pi}\left(1+2\cos{\theta}+\frac{1+\cos{2\theta}}{2}\right){d\theta}
=\frac{{\pi}a^{2}}{2}+a^{2}\int_{\frac{\pi}{2}}^{\pi}\left(\frac{3}{2}+2\cos{\theta}+\frac{1}{2}\cos{2\theta}\right){d\theta}

=\frac{{\pi}a^{2}}{2}+a^{2}\left[\frac{3}{2}{\theta}\right]_{\frac{\pi}{2}}^{\pi}+2a^{2}\left[\sin{\theta}\right]_{\frac{\pi}{2}}^{\pi}+\frac{a^{2}}{2}\left[\frac{\sin{2\theta}}{2}\right]_{\frac{\pi}{2}}^{\pi}

=\frac{{\pi}a^{2}}{2}+\frac{3}{2}{\pi}a^{2}-\frac{3}{4}{\pi}a^{2}-2a^{2}\\

=\left(\frac {2{\pi}a^{2}+6{\pi}a^{2}-3{\pi}a^{2}}{4}-2a^{2}\right)

=\frac{5}{4}{\pi}a^{2}-2a^{2}

=\left(\frac{5}{4}{\pi}-2\right)a^{2}

(b):r=a\left(1+\cos{\theta}\right),r=a\left(1-\cos{\theta}\right)

Solution:r=a\left(1+\cos{\theta}\right),r=a\left(1-\cos{\theta}\right)

अभीष्ट क्षेत्रफल=4×\frac{1}{2}\int_{0}^{\frac{\pi}{2}}r^{2}{d\theta}

=2\int_{0}^{\frac{\pi}{2}}a^{2}\left(1-\cos{\theta}\right)^{2}{d\theta}
=2a^{2}\int_{0}^{\frac{\pi}{2}}\left(1-2\cos{\theta}+\cos^{2}{\theta}\right){d\theta}
=2a^{2}\int_{0}^{\frac{\pi}{2}}\left(1-2\cos{\theta}+\frac{1+\cos{2\theta}}{2}\right){d\theta}
=3a^{2}\int_{0}^{\frac{\pi}{2}}{d\theta}-4a^{2}\int_{0}^{\frac{\pi}{2}}\cos{\theta}{d\theta}+a^{2}\int_{0}^{\frac{\pi}{2}}\cos{2\theta}{d\theta}

=3a^{2}\left[{\theta}\right]_{0}^{\frac{\pi}{2}}-4a^{2}\left[\sin{\theta}\right]_{0}^{\frac{\pi}{2}}+\frac{a^{2}}{2}\left[\sin{2\theta}\right]_{0}^{\frac{\pi}{2}}

=3a^{2}.\frac{\pi}{2}-4a^{2}.1+0\\

=\frac{a^{2}}{2}\left({3\pi}-8\right)\\

Example:5.वृत्त r=2a\cos{\theta} के बाहर एवं कार्डिआइड r=a\left(1+\cos{\theta}\right) के अन्दर का क्षेत्रफल ज्ञात कीजिए। (Find the area situated outside the circle r=2a\cos{\theta} inside the cardioid r=a\left(1+\cos{\theta}\right)\\.)

Solution:वृत्त:r=2a\cos{\theta} …(1)

कार्डिआइड:r=a\left(1+\cos{\theta}\right) …(2)

अभीष्ट क्षेत्रफल=कार्डिआइड का क्षेत्रफल- वृत्त का क्षेत्रफल कार्डिआइड का क्षेत्रफल=

=2×\frac{1}{2}\int_{0}^{\pi}r^{2}{d\theta}

=\int_{0}^{\pi}a^{2}\left(1+\cos{\theta}\right)^{2}{d\theta}
=a^{2}\int_{0}^{\pi}\left(2\cos^{2}{\frac{\theta}{2}}\right)^{2}{d\theta}
=4a^{2}\int_{0}^{\pi}\cos^{4}{\frac{\theta}{2}}{d\theta}
\text{Put }\frac{\theta}{2}={\phi}
\Rightarrow{d\theta}={2d\phi}
\text{जब }{\theta}=0 \text{ तो }{\phi}=0
\text{जब }{\theta}={\pi} \text{ तो }{\phi}=\frac{\pi}{2}
=8a^{2}\int_{0}^{\frac{\pi}{2}}\cos^{4}{\phi}{d\phi}
=8a^{2}\frac{\Gamma{\left(\frac{4+1}{2}\right)}\Gamma{\left(\frac{1}{2}\right)}}{2\Gamma{\left(\frac{4+0+2}{2}\right)}}
=4a^{2}\frac{\frac{3}{2}.\frac{1}{2}\sqrt{\pi}\sqrt{\pi}}{2}
=\frac{3}{2}{\pi}a^{2}
वृत्त की समीकरण:r=2a\cos{\theta}
\Rightarrow{r^{2}}=2ar\cos{\theta}
\Rightarrow{x^{2}+y^{2}}=2ax(कार्तीय निर्देशांकों में)
जिसका केन्द्र (a,0) तथा त्रिज्या=a
अतः वृत्त का क्षेत्रफल={\pi}a^{2}
अभीष्ट क्षेत्रफल=\frac{3}{2}{\pi}a^{2}-{\pi}a^{2}
=\frac{1}{2}{\pi}a^{2}
Example:6.द्वि-समाकलन से वृत्त r=a\sin{\theta} के भीतर एवं कार्डिआइड r=a\left(1-\cos{\theta}\right) के बाहर का क्षेत्रफल ज्ञात कीजिए।
(Find by double integration the area lying inside the circle r=a\sin{\theta} and outside the cardioid r=a\left(1-\cos{\theta}\right).)
Solution:वृत्त:r=a\sin{\theta}
कार्डिआइड:r=a\left(1-\cos{\theta}\right)
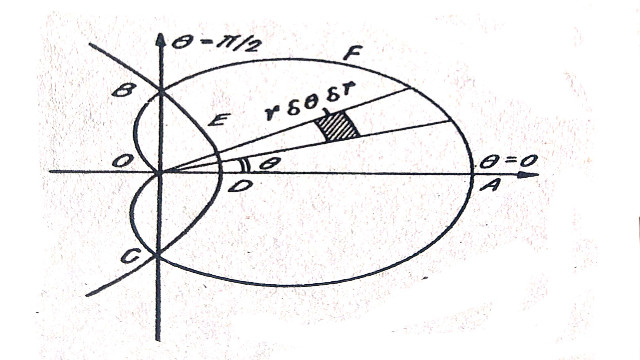
अभीष्ट क्षेत्रफल=क्षेत्रफलOFAEO
=\int_{{\theta}=0}^{\frac{\pi}{2}}\int_{\text{r for cardioid}}^{\text{r for circle}}r{d\theta}dr
=\int_{{\theta}=0}^{\frac{\pi}{2}}\int_{a\left(1-\cos{\theta}\right)}^{a\sin{\theta}}r{d\theta}dr

=\int_{0}^{\frac{\pi}{2}}\left[\frac{r^{2}}{2}\right]{a\left(1-\cos{\theta}\right)}^{a\sin{\theta}}{d\theta}
=\frac{1}{2}\int_{0}^{\frac{\pi}{2}}\left[a^{2}\sin^{2}{\theta}-a^{2}\left(1-\cos{\theta}\right)^{2}\right]{d\theta}

=\frac{a^{2}}{2}\int_{0}^{\frac{\pi}{2}}\left(\sin^{2}{\theta}-\cos^{2}{\theta}-1+2\cos{\theta}\right){d\theta}

=\frac{a^{2}}{2}\left[\frac{\Gamma{\left(\frac{2+1}{2}\right)}\Gamma{\left(\frac{1}{2}\right)}}{2\Gamma{\left(\frac{2+0+2}{2}\right)}}-\frac{\Gamma{\left(\frac{2+1}{2}\right)}\Gamma{\left(\frac{1}{2}\right)}}{2\Gamma{\left(\frac{2+0+2}{2}\right)}}\right]-\frac{a^{2}}{2}\left[{\theta}\right]{0}^{\frac{\pi}{2}}+\frac{a^{2}}{2}2\left[\sin{\theta}\right]_{0}^{\frac{\pi}{2}}

=a^{2}-\frac{{\pi}a^{2}}{4}
=\frac{\left(4-{\pi}\right)a^{2}}{4}
Example:7.द्वि-समाकल से कार्डिआइड r=1+\cos{\theta} के भीतर एवं परवलय r\left(1+\cos{\theta}\right)=1 के बाहर का क्षेत्रफल ज्ञात कीजिए।
(Find the double integration the area lying inside the cardioid r=1+\cos{\theta} and outside the parabola r\left(1+\cos{\theta}\right)=1.)

Solution:कार्डिआइड:r=1+\cos{\theta}
परवलय:r\left(1+\cos{\theta}\right)=1
अभीष्ट क्षेत्रफल=क्षेत्रफल CAFBEDC
=2× क्षेत्रफल DAFBED
=2\int_{0}^{\frac{\pi}{2}}\int_{\text{r for parabola}}^{\text{r for cardioid}}r{d\theta}dr
=2\int_{0}^{\frac{\pi}{2}}\int_{\frac{1}{1+\cos{\theta}}}^{1+\cos{\theta}}r{d\theta}dr

=\int_{0}^{\frac{\pi}{2}}\left[r^{2}\right]{\frac{1}{1+\cos{\theta}}}^{1+\cos{\theta}}{d\theta}
=\int_{0}^{\frac{\pi}{2}}\left(1+\cos{\theta}\right)^{2}{d\theta}-\int_{0}^{\frac{\pi}{2}}\frac{1}{\left(1+\cos{\theta}\right)^{2}}{d\theta} …(1)

अब=\int_{0}^{\frac{\pi}{2}}\left(1+\cos{\theta}\right)^{2}{d\theta}
=\int_{0}^{\frac{\pi}{2}}\left(1+2\cos{\theta}+\cos^{2}{\theta}{d\theta}\right){d\theta}
=\int_{0}^{\frac{\pi}{2}}\left(1+2\cos{\theta}+\frac{1+2\cos{2\theta}}{2}\right){d\theta}
=\int_{0}^{\frac{\pi}{2}}\left(\frac {3}{2}+2\cos{\theta}+\frac{1}{2}\cos{2\theta}\right){d\theta}

=\left[\frac{3}{2}{\theta}\right]_{0}^{\frac{\pi}{2}}+2\left[\sin{\theta}\right]_{0}^{\frac{\pi}{2}}+\frac{1}{4}\left[\sin{2\theta}\right]_{0}^{\frac{\pi}{2}}

=\frac{3\pi}{4}+2 …(2)

तथा \int_{0}^{\frac{\pi}{2}}\frac{1}{\left(1+\cos{\theta}\right)^{2}}{d\theta}

=\int_{0}^{\frac{\pi}{2}}\frac{1}{2\cos^{4}\frac{\theta}{2}}{d\theta}
=\frac{1}{2}\int_{0}^{\frac{\pi}{2}}\sec^{4}\frac{\theta}{2}{d\theta}
=\frac{1}{2}\int_{0}^{\frac{\pi}{2}}\left(1+\tan^{2}\frac{\theta}{2}\right)\sec^{2}\frac{\theta}{2}{d\theta}
\text{Put }\tan{\frac{\theta}{2}}=t
\Rightarrow{\frac{1}{2}}\sec^{2}\frac{\theta}{2}{d\theta}=dt
\text{जब }{\theta}=0\text{ तो }t=0
\text{जब }{\theta}=\frac{\pi}{2}\text{ तो }t=1
=\frac{1}{2}\int_{0}^{1}\left(1+t^{2}\right)dt

\Rightarrow{\frac{1}{2}}\left[t+\frac{1}{3}t^{3}\right]<em>{0}^{1}

=\frac{2}{3} …(3)

समीकरण (2) व (3) से (1) में मान रखने पर:

अभीष्ट क्षेत्रफल=\frac{3\pi}{4}+2-\frac{2}{3}

=\left(\frac{3\pi}{4}+\frac{4}{3}\right)

Example:8.द्वि-समाकलन से xy-समतल में उस भाग का क्षेत्रफल ज्ञात कीजिए जो लेमीनीस्केट r^{2}=a^{2}\cos{2\theta} से घिरा हुआ है। (Find the double integration the area of that part in xy-plane which is bounded by the lemniscate r^{2}=a^{2}\cos{2\theta}.)

Solution:r^{2}=a^{2}\cos{2\theta}

अभीष्ट क्षेत्रफल=

=4\int_{{\theta}=0}^{\frac{\pi}{4}}\int_{r=0}^{f\left({\theta}\right)}r{d\theta}dr

=4\int_{0}^{\frac{\pi}{4}}\int_{0}^{a\sqrt{\cos{2\theta}}}rdr{d\theta}

=4\int_{0}^{\frac{\pi}{4}}\left[r^{2}\right]_{0}^{a\sqrt{\cos{2\theta}}}{d\theta}
=4\int_{0}^{\frac{\pi}{4}}a^{2}\cos{2\theta}{d\theta}
=2a^{2}\left[\frac{\sin{2\theta}}{2}\right]{0}^{\frac{\pi}{4}}

=a^{2}{1}

=a^{2}

Example:9.लेमीनीस्केट r^=a^{2}\sin{2\theta} के एक लूप का द्रव्यमान ज्ञात कीजिए जिसका घनत्व {\rho}=kr^{2} प्रतिवर्ग क्षेत्र है। (Find the mass of the loop of the lemniscate r^=a^{2}\sin{2\theta} if the density per unit area is {\rho}=kr^{2}.)

Solution:लेमीनीस्केट:r^=a^{2}\sin{2\theta}

द्रव्यमान M={\int}\int_{A}f\left(r,{\theta}\right)r{d\theta}dr

=\int_{0}^{\frac{\pi}{2}}\int_{0}^{a\sqrt{\sin{2\theta}}}\left(kr^{2}\right)r{d\theta}dr

=_{0}^{\frac{\pi}{2}}k\left[\frac{r^{4}}{4}\right]{0}^{a\sqrt{\sin{2\theta}}}{d\theta}
=\frac{ka^{4}}{4}\int{0}^{\frac{\pi}{2}}\sin^{2}{2\theta}{d\theta}

=\frac{ka^{4}}{4}\int_{0}^{\frac{\pi}{2}}\frac{1-\cos{2\theta}}{2}

=\frac{ka^{4}}{4}\left[\frac{\theta}{2}\right]_{0}^{\frac{\pi}{2}}-\frac{ka^{4}}{4}\left[\frac{\sin{4\theta}}{4}\right]_{0}^{\frac{\pi}{2}}

=\frac{{\pi}ka^{4}}{16}
उपर्युक्त उदाहरणों के द्वारा समाकल में क्षेत्रकलन विधि (Quadrature Method in Integrals),ध्रुवीय समीकरणों वाले वक्रों तथा ध्रुवान्तर रेखाओं से परिबद्ध क्षेत्रफल (Area Bounded by Curves in Polar Equations and Radii Vectors) को समझ सकते हैं।

Also Read This Article:Surface Area of Solids of Revolution

3.समाकल में क्षेत्रकलन विधि (Quadrature Method in Integrals),ध्रुवीय समीकरणों वाले वक्रों तथा ध्रुवान्तर रेखाओं से परिबद्ध क्षेत्रफल (Area Bounded by Curves in Polar Equations and Radii Vectors) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:

• उपर्युक्त प्रश्नों के उत्तर द्वारा समाकल में क्षेत्रकलन विधि (Quadrature Method in Integrals),ध्रुवीय समीकरणों वाले वक्रों तथा ध्रुवान्तर रेखाओं से परिबद्ध क्षेत्रफल (Area Bounded by Curves in Polar Equations and Radii Vectors) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।

Quadrature Method in Integrals

समाकल में क्षेत्रकलन विधि
(Quadrature Method in Integrals)

Quadrature Method in Integrals

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Instagram	click here
4.	Linkedin	click here
5.	Facebook Page	click here
6.	Twitter	click here