1.समाकलन गणित में क्षेत्रकलन (Quadrature in Integral Calculus),समाकलन गणित में क्षेत्रकलन विधि (Quadrature Method in Integral Calculus):

• समाकलन गणित में क्षेत्रकलन (Quadrature in Integral Calculus) विधि वक्रों अथवा सरल रेखाओं अथवा दोनों से घिरे हुए क्षेत्र का क्षेत्रफल ज्ञात करने में प्रयुक्त की जाती है।क्षेत्रकलन से सम्बन्धित थ्योरी व सूत्रों को इसके पूर्व आर्टिकल में बताया गया है।इसलिए थ्योरी व सूत्रों हेतु इससे पूर्व आर्टिकल को देखना चाहिए।
• आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:Surface Area of Solids of Revolution

2.समाकलन गणित में क्षेत्रकलन पर आधारित उदाहरण (Examples Based on Quadrature in Integral Calculus):

Example:1.निम्नलिखित वक्रों तथा उनके अनन्तस्पर्शी से घिरा हुआ क्षेत्रफल ज्ञात कीजिए:
(Find the area bounded by the following curves and their asymptotes):
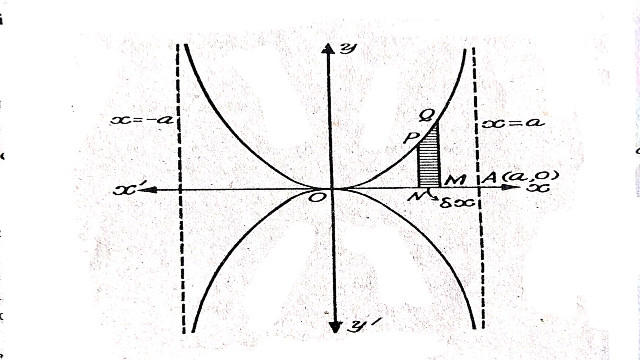
(a):x^{2}y^{2}=a^{2}\left(y^{2}-x^{2}\right)

Solution:x^{2}y^{2}=a^{2}\left(y^{2}-x^{2}\right)
अनन्तस्पर्शी ज्ञात करने हेतु y की उच्चतम घात का गुणांक=0
x^{2}-y^{2}=0
\Rightarrow x=\pm{a}
अतः x का मान 0 से a तक बढ़ता है।
अभीष्ट क्षेत्रफल=
=4 × \int_{0}^{a} ydx
=4 × \int_{0}^{a}\frac{ax}{\sqrt{\left(a^{2}-x^{2}\right)}}
\text{ Put }x=a\sin{\theta}
\Rightarrow dx=a\cos{\theta}{d\theta}
\text{जब }x=0 \text{ तो }{\theta}=0
\text{जब }x=a \text{ तो }{\theta}=\frac{\pi}{2}
=4 × \int_{0}^{\frac{\pi}{2}}\frac{a\left(a\sin{\theta}\right)\left(a\cos{\theta}{d\theta}\right)}{\sqrt{\left(a^{2}-a^{2}\sin^{2}{\theta}\right)}}
=4a^{2} × \int_{0}^{\frac{\pi}{2}}\frac{\left(\sin{\theta}\right)\left(\cos{\theta}{d\theta}\right)}{\sqrt{\left(1-\sin^{2}{\theta}\right)}}
=4a^{2} × \int_{0}^{\frac{\pi}{2}}\frac{\left(\sin{\theta}\right)\left(\cos{\theta}{d\theta}\right)}{\cos{\theta}}
=4a^{2} × \int_{0}^{\frac{\pi}{2}}\sin{\theta}
=4a^{2}\left[-\cos{\theta}\right]_{0}^{\frac{\pi}{2}}

=4a^{2}\left[-\cos{\frac{\pi}{2}}+\cos{0}\right]

=4a^{2}

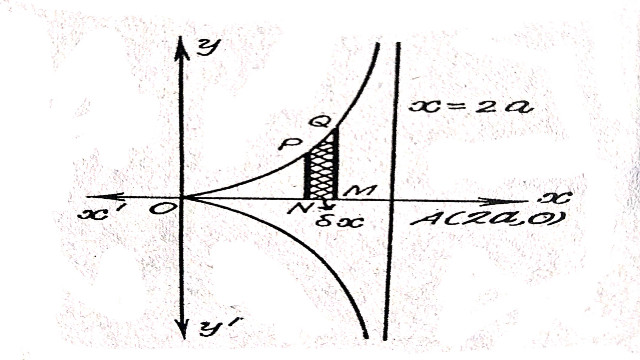
(b):y^{2}\left(2a-x\right)=x^{3}

Solution:y^{2}\left(2a-x\right)=x^{3}

\Rightarrow y^{2}=\frac{x^{\frac{3}{2}}}{\left(2a-x\right)}\\

\Rightarrow y^{2}=\frac{x^{2}}{\left(2a-x\right)}\\

\Rightarrow y^{2}=\frac{x^{\frac{3}{2}}}{\sqrt{\left(2a-x\right)}}

अनन्तस्पर्शी ज्ञात करने हेतु y की उच्चतम घात का गुणांक=0

\Rightarrow 2a-x=0 \Rightarrow x=2a

अभीष्ट क्षेत्रफल= =

=2\int_{0}^{2a} ydx

=2\int_{0}^{2a}\frac{x^{\frac{3}{2}}}{\sqrt{\left(2a-x\right)}}

\text{ Put }x=2a\sin^{2}{\theta}

dx=4a\sin{\theta}\cos{\theta}

\text{जब }x=0 \text{ तो }{\theta}=0

\text{जब }x=2a \text{ तो }{\theta}=\frac{\pi}{2}
=2\int_{0}^{\frac{\pi}{2}}\frac{\left(2a\sin^{2}{\theta}\right)^{\frac{3}{2}}}{\sqrt{\left(2a-2a\sin^{2}{\theta}\right)}}.4a\sin{\theta}\cos{\theta}{d\theta}
=8a\int_{0}^{\frac{\pi}{2}}\frac{2\sqrt{2}a^{\frac{3}{2}}\sin^{3}{\theta}\left(\sin{\theta}\cos{\theta}\right){d\theta}}{\sqrt{2a}\sqrt{1-\sin^{2}{\theta}}}
=16a^{2}\int_{0}^{\frac{\pi}{2}}\frac{\sin^{4}{\theta}\cos{\theta}}{\cos{\theta}}{d\theta}
=16a^{2}\int_{0}^{\frac{\pi}{2}}\sin^{4}{\theta}{d\theta}
=16a^{2}\frac{\Gamma{\left(\frac{4+1}{2}\right)}\Gamma{\left(\frac{1}{2}\right)}}{2\Gamma{\left(\frac{4+0+2}{2}\right)}}
=16a^{2}.\frac{\frac{3}{2}.\frac{1}{2}\sqrt{\pi}\sqrt{\pi}}{2 × 2}
=3{\pi}a^{2}
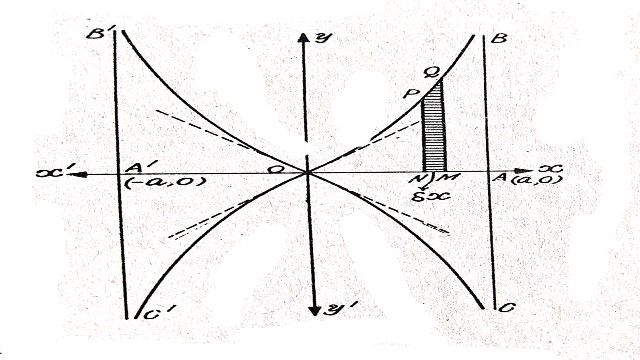
(c):x^{2}\left(x^{2}+y^{2}\right)=a^{2}\left(y^{2}-x^{2}\right)

Solution:x^{2}\left(x^{2}+y^{2}\right)=a^{2}\left(y^{2}-x^{2}\right)

\Rightarrow x^{4}+x^{2}y^{2}=a^{2}y^{2}-a^{2}x^{2}

\Rightarrow a^{2}y^{2}-x^{2}y^{2}=a^{2}y^{2}+a^{2}x^{2}
\Rightarrow y^{2}\left(a^{2}-x^{2}\right)=x^{2}\left(a^{2}+x^{2}\right)
\Rightarrow y=x\sqrt{\frac{a^{2}+x^{2}}{a^{2}-x^{2}}}
अनन्तस्पर्शी ज्ञात करने हेतु y की उच्चतम घात का गुणांक=0
\Rightarrow a^{2}-x^{2}=0
\Rightarrow x=\pm{a}
अतः x>a के लिए वक्र का अस्तित्व नहीं है।
अभीष्ट क्षेत्रफल=
=4 \int_{0}^{a} ydx
=4 × \int_{0}^{a}x\sqrt{\frac{a^{2}+x^{2}}{a^{2}-x^{2}}}
=4 \int_{0}^{a} ydx
=4 × \int_{0}^{a}x\sqrt{\frac{\left(a^{2}+x^{2}\right)^{2}}{a^{2}-x^{2}}}
=4 × \int_{0}^{a}x\frac{\left(a^{2}+x^{2}\right)}{\sqrt{a^{4}-x^{4}}}
\text{ Put }x^{2}=a^{2}\sin{\theta}
2xdx=a^{2}\cos{\theta}{d\theta}
\text{जब }x=0 \text{ तो }{\theta}=0
\text{जब }x=a \text{ तो }{\theta}=\frac{\pi}{2}
=2 \int_{0}^{\frac{\pi}{2}}\frac{\left(a^{2}+a^{2}\sin{\theta}\right)}{\sqrt{a^{4}-a^{4}\sin^{2}{\theta}}}a^{2}\cos{\theta}{d\theta}
=2a^{2} \int_{0}^{\frac{\pi}{2}}\frac{\left(1+\sin{\theta}\right)\cos{\theta}}{\sqrt{1-\sin^{2}{\theta}}}{d\theta}
=2a^{2} \int_{0}^{\frac{\pi}{2}}\left(1+\sin{\theta}\right){d\theta}
=2a^{2}\left[{\theta}-\cos{\theta}\right]_{0}^{\frac{\pi}{2}}

=2a^{2}\left[\frac{\pi}{2}+1\right]

Example:2.निम्नलिखित वक्रों के बीच घिरा हुआ क्षेत्रफल ज्ञात कीजिए: (Find the area included between the following curves):

(a):x^{2}+y^{2}=8 तथा (and) y^{2}=2x

Solution:x^{2}+y^{2}=8 तथा (and) y^{2}=2x

x^{2}+y^{2}=8…(1)

y^{2}=2x    …(2)

दोनों के प्रतिच्छेद बिन्दु हेतु (1) व (2) से:

x^{2}+2x=8

\Rightarrow x^{2}+4x-2x-8=0\\

\Rightarrow x\left(x+4\right)-2\left(x+4\right)=0\\

\Rightarrow \left(x+4\right)\left(x-2\right)=0\\

\Rightarrow x=2,x=-4\left(\text{ असंभव है }\right)\\

y^{2}=2x\Rightarrow y^{2}=2×2\\

\Rightarrow y=\pm{2}

प्रतिच्छेद बिन्दु (2,2),(2,-2) अतः दोनों वक्रों से घिरा हुआ अभीष्ट क्षेत्रफल=

=2\int_{0}^{2} ydx\left(\text{ परवलय से }\right)+2\int_{2}^{2\sqrt{2}} ydx\left(\text{ वृत्त से }\right)

=2\int_{0}^{2}\sqrt{2x}dx+2\int_{0}^{2\sqrt{2}}\sqrt{8-x^{2}}dx
=2\sqrt{2}\frac{2}{3}\left[x^{\frac{3}{2}}\right]_{0}^{2}+2\left[\frac{x}{2}\sqrt{8-x^{2}}+\frac{8}{2}\sin^{-1}\left(\frac{x}{2\sqrt{2}}\right)\right]_{2}^{2\sqrt{2}}

=\frac{4\sqrt{2}}{3}.2\sqrt{2}+2\left[4\sin^{-1}\left(1\right)-2-4\sin^{-1}\left(\frac{1}{\sqrt{2}}\right)\right]
=\frac{16}{3}+2\left[4 × \frac{\pi}{2}-2-4 × \frac{\pi}{4}\right]
=\frac{16}{3}+2\left({\pi}-2\right)
=\frac{4}{3}+2{\pi}
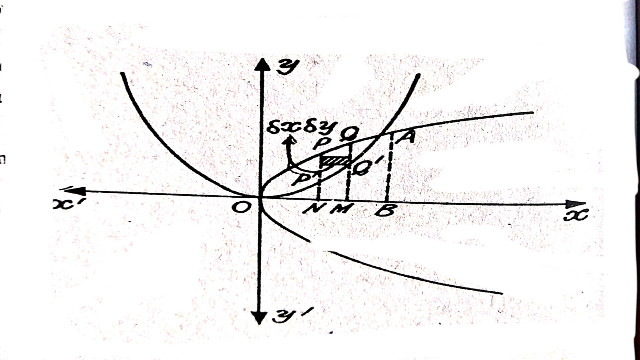
(b):y^{2}=4ax तथा (and) x^{2}=4ay

Solution:y^{2}=4ax तथा (and) x^{2}=4ay
y^{2}=4ax …(1)
x^{2}=4ay …(2}
समीकरण (1) और (2) से:
\left(\frac{y^{2}}{4a}\right)^{2}=4ay
\Rightarrow y^{4}=64a^{3}y
\Rightarrow y^{4}-64a^{3}y=0
\Rightarrow y\left(y^{3}-64a^{3}\right)=0
\Rightarrow y=0,\left(y-4a\right)\left(y^{2}+4ay+16a^{2}\right)=0
y=0,4a
x=0,4a
अतः प्रतिच्छेद बिन्दु (a,0),(4a,4a)
अभीष्ट क्षेत्रफल=
=\int_{0}^{4a} ydx\left(y^{2}=4ax \text{ परवलय से }\right)-\int_{0}^{4a} ydx\left(x^{2}=4ay\text{ परवलय से }\right)
=\int_{0}^{4a}\sqrt{4ax} dx-\int_{0}^{4a}\frac{x^{2}}{4a} dx
=2\sqrt{a}.\frac{2}{3}\left[x^{\frac{3}{2}}\right]_{0}^{4a}-\frac{1}{4a}\left[\frac{x^{3}}{3}\right]_{0}^{4a}

=\frac{4\sqrt{a}}{3}\left(8a^{\frac{3}{2}}\right)-\frac{1}{12a}×64a^{3}
=\frac{32}{3}a^{2}-\frac{16}{3}a^{2}
=\frac{16}{3}a^{2}
(c):y^{2}=2ax-x^{2} तथा (and) y^{2}=ax

Solution:y^{2}=2ax-x^{2} तथा (and) y^{2}=ax
y^{2}=2ax-x^{2} …(1)
y^{2}=ax …(2)
समीकरण (1) व (2) से:
ax=2ax-x^{2}
\Rightarrow x^{2}-ax=0
\Rightarrow x\left(x-a\right)
x=0,a
y=,\pm{a}
अतः वृत्त तथा परवलय का प्रतिच्छेद बिन्दु (0,0),(a,a),(a,-a)
अभीष्ट क्षेत्रफल=
2\int_{0}^{a} ydx\left(\text{ परवलय से }\right)+2\int_{a}^{2a}\left(\text{ वृत्त से }\right)
=2\int_{0}^{a}\sqrt{ax} dx+2\int_{a}^{2a}\sqrt{2ax-x^{2}} dx
=2\sqrt{a}\frac{2}{3}\left[x^{\frac{3}{2}}\right]_{0}^{a}+2\int_{a}^{2a}\sqrt{a^{2}-\left(x-a\right)^{2}} dx

=2.\frac{2}{3}\sqrt{a}a^{\frac{3}{2}}+2\left[\frac{x-a}{2}\sqrt{2ax-x^{2}}+\frac{a^{2}}{2}\sin^{-1}\left(\frac{x-a}{a}\right)\right]_{a}^{2a}\\

\Rightarrow 2 ×\frac{2}{3}a^{2}+2\left[\frac{a^{2}}{2}\sin^{-1}\left(1\right)\right]\\

\Rightarrow 2 × \frac{2}{3}a^{2}+2 × \frac{a^{2}}{2}\frac{\pi}{2}\\

\Rightarrow 2a^{2}\left(\frac{\pi}{4}+\frac{2}{3}\right)

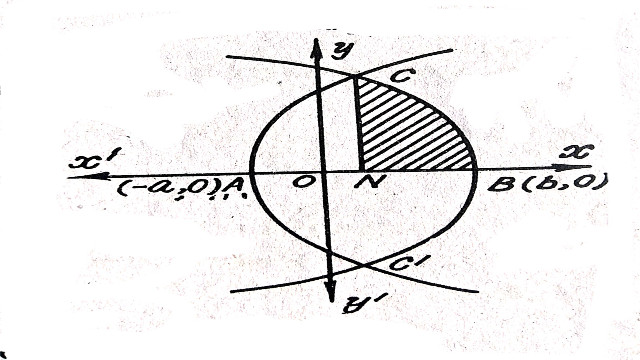
(d):y^{2}=4a\left(x+a\right) तथा (and) y^{2}=4b\left(b-x\right)

Solution:y^{2}=4a\left(x+a\right) तथा (and) y^{2}=4b\left(b-x\right)\\ y^{2}=4a\left(x+a\right) का शीर्ष A(-a,0) तथा नाभिलम्ब=4a

तथा परवलय y^{2}=4b\left(b-x\right) का शीर्ष B(b,0) तथा नाभिलम्ब= 4b

y^{2}=4a\left(x+a\right) …(1)

y^{2}=4b\left(b-x\right) …(2)

समीकरण (1) व (2) से:

4a\left(x+a\right)=4b\left(b-x\right)\\

\Rightarrow x\left(a+b\right)=\left(b^{2}-a^{2}\right)\\

\Rightarrow x=b-a

दोनों परवलयों का प्रतिच्छेद बिन्दु जिनका भुज= b-a

अभीष्ट क्षेत्रफल=

=2\int_{b-a}^{b} ydx\left[\text{ परवलय } (2) \text { से }\right]+2\int_{-a}^{b-a} ydx\left[\text{ परवलय } (1) \text{ से }\right]

=2\int_{b-a}^{b}\sqrt{4b\left(b-x\right)} dx+2\int_{-a}^{b-a}\sqrt{4a\left(a+x\right)} dx

=4\sqrt{b}\left[-\frac{2}{3}\left(b-x\right)^{\frac{3}{2}}\right]_{b-a}^{b}+4\sqrt{a}\left[\frac{2}{3}\left(a+x\right)^{\frac{3}{2}}\right]_{-a}^{b-a}

=\frac{8}{3}\sqrt{b}a^{\frac{3}{2}}+\frac{8}{3}\sqrt{a}b^{\frac{3}{2}}

=\frac{8}{3}\left(a+b\right)

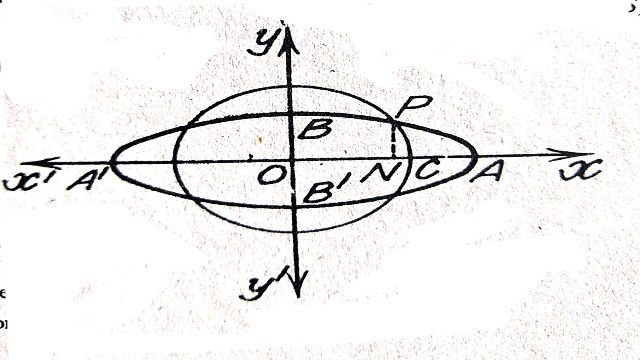
(e):x^{2}+y^{2}=4 तथा (and) x^{2}+4y^{2}=9

Solution:x^{2}+y^{2}=4 तथा (and) x^{2}+4y^{2}=9
x^{2}+y^{2}=4 …(1)
x^{2}+4y^{2}=9 …(2)
समीकरण (1) व (2) से:
3y^{2}=5
\Rightarrow y=\pm{\sqrt{\frac{5}{3}}}
x^{2}=4-\left(\frac{5}{3}\right)
\Rightarrow x^{2}=\frac{7}{3}
\Rightarrow y=\pm{\sqrt{\frac{7}{3}}}
अतः वृत्त व दीर्घवृत्त का प्रतिच्छेद बिन्दु \pm{\sqrt{\frac{7}{3}}},\pm{\sqrt{\frac{5}{3}}}
अभीष्ट क्षेत्रफल=
=4 × \int_{0}^{\sqrt{\frac{7}{3}}} ydx\left(\text{ दीर्घवृत्त से }\right)+4 × \int_{\sqrt{\frac{7}{3}}}^{2} ydx\left(\text{ वृत्त से }\right)
=4\int_{0}^{\sqrt{\frac{7}{3}}}\left[\frac{1}{2}\sqrt{9-x^{2}}\right] dx+4 × \left[\int_{\sqrt{\frac{7}{3}}}^{2}\sqrt{\left(4-x^{2}\right)}dx\right]
=2\left[\frac{x}{2}\sqrt{\left(9-x^{2}\right)}+\frac{9}{2}\sin^{-1}\left(\frac{x}{3}\right)\right]_{0}^{\sqrt{\frac{7}{3}}}\\+4\left[\frac{x}{2}\sqrt{\left(4-x^{2}\right)}+2\sin^{-1}\left(\frac{x}{2}\right)\right]_{\sqrt{\left(\frac{7}{3}\right)}}^{2}

=2\left[\frac{1}{2}\sqrt{\left(\frac{7}{3}\right)}\sqrt{\left(\frac{20}{3}\right)}+\frac{9}{2}\sin^{-1}\left\{\frac{1}{3}\sqrt{\left(\frac{7}{3}\right)}\right\}\right]+4\left[2\sin^{-1}\left(1\right)-\frac{1}{2}\sqrt{\left(\frac{7}{3}\right)}\sqrt{\left(\frac{5}{3}\right)}-2\sin^{-1}\left(\frac{1}{2}\sqrt{\left(\frac{7}{3}\right)}\right)\right]
=4{\pi}+9\sin^{-1}\left(\frac{1}{3}\sqrt{\left(\frac{7}{3}\right)}\right)-8\sin^{-1}\left(\frac{1}{2}\sqrt{\left(\frac{7}{3}\right)}\right)
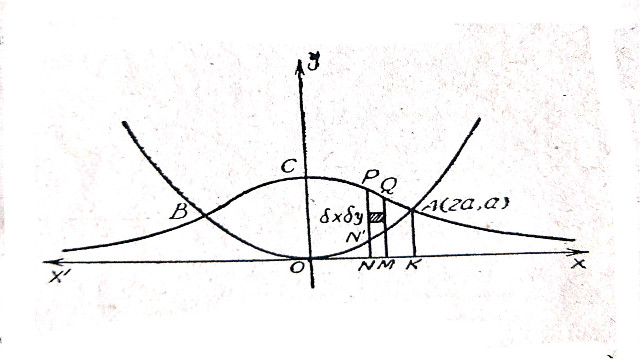
(f):x^{2}=4ay तथा (and) y\left(x^{2}+4a^{2}\right)=8a^{3}

Solution:x^{2}=4ay तथा (and) y\left(x^{2}+4a^{2}\right)=8a^{3}
x^{2}=4ay …(1)
y\left(x^{2}+4a^{2}\right)=8a^{3} …(2)
समीकरण (1) व (2) से:
\frac{x^{2}}{4a}\left(x^{2}+4a^{2}\right)=8a^{3}
\Rightarrow x^{4}+4a^{2}x^{2}=32a^{4}
\Rightarrow x^{4}+4a^{2}x^{2}-32a^{4}=0
\Rightarrow x^{4}+8a^{2}x^{2}-4a^{2}x^{2}-32a^{4}=0
\Rightarrow x^{2}\left(x^{2}+8a^{2}\right)-4a^{2}\left(x^{2}+8a^{2}\right)=0
\Rightarrow \left(x^{2}-4a^{2}\right)\left(x^{2}+8a^{2}\right)=0
\Rightarrow \left(x^{2}-4a^{2}\right)=0
\Rightarrow \left(x^{2}=4a^{2}\right)
\Rightarrow x=\pm{2a}
y=a
अतः दोनों वक्रों का प्रतिच्छेद बिन्दु= (2a,a) तथा (-2a,a)
अभीष्ट क्षेत्रफल=
=2\int_{x=0}^{2a}\int_{y=\text{NN'}}^{\text{PN}} dxdy
\text{ जहाँ }\text{ NN'}=\frac{x^{2}{4a}},\text{ PN }=\frac{8a^{3}}{x^{2}+4a^{2}}
=2\int_{x=0}^{2a}\left[y\right]_{\text{NN'}}^{\text{PN}} dxdy

=2\int_{x=0}^{2a}\left(\text{PN}-\text{NN'}\right) dx

=2\int_{0}^{2a}\left[\frac{8a^{3}}{x^{2}+4a^{2}}-\frac{x^{2}}{4a}\right] dx
=16a^{2}\int_{0}^{2a}\frac{8a^{3}}{x^{2}+4a^{2}}dx-\frac{a}{2}\int_{0}^{2a}x^{2}dx
=16a^{2}\left[\frac{1}{2a}\tan^{-1}\left(\frac{x}{2a}\right)\right]_{0}^{2a}-\frac{1}{2a}\left[\frac{x^{3}}{3}\right]_{0}^{2a}

=8a^{2}\left[\tan^{-1}\left(1\right)-\tan^{-1}\left(0\right)\right]-\left(\frac{4a^{2}}{3}\right)
=8a^{2}\left(\frac{\pi}{4}\right)-\left(\frac{4a^{2}}{3}\right)
=\left[2{\pi}--\left(\frac{4}{3}\right)\right]a^{2}
Example:3.सिद्ध कीजिए कि उन दो क्षेत्रफलों में से जिनमें वृत्त x^{2}+y^{2}=64a^{2}, परवलय y^{2}=12ax द्वारा विभाजित होता है, बड़े भाग का क्षेत्रफल होगा।
(Prove that larger of the two areas into which the circle x^{2}+y^{2}=64a^{2} is divided by the parabola y^{2}=12ax is \frac{16}{3}a^{2}\left(8{\pi}-\sqrt{3}\right).)

Solution:y^{2}=12ax परवलय का शीर्ष (0,0) तथा नाभिलम्ब =12a
x^{2}+y^{2}=64a^{2} वृत्त का केन्द्र (0,0) तथा त्रिज्या=8a
y^{2}=12ax …(1)
x^{2}+y^{2}=64a^{2} …(2)
समीकरण (1) व (2) से:
x^{2}+12ax-64a^{2}=0
\Rightarrow x^{2}+16ax-4ax-64a^{2}=0
\Rightarrow x\left(x+16\right)-4a\left(x+16a\right)
\Rightarrow \left(x+16a\right)\left(x-4a\right)=0
\Rightarrow x=4a,x=-16a \text{ असंभव है }
y=\pm{4\sqrt{3}a}
अतः दोनों वक्रों के प्रतिच्छेद बिन्दु
\left(4a,\pm{4\sqrt{3}a}\right)
अभीष्ट क्षेत्रफल= छायांकित भाग
=वृत्त का क्षेत्रफल-क्षेत्रफल OP’APO
{\pi}\left(8a\right)^{2}-2\int_{0}^{4a} ydx\left(\text{ परवलय से}\right)-2\int_{4a}^{8a} ydx\left(\text{ वृत्त से}\right)
=64{\pi}a^{2}-2\int_{0}^{4a}\sqrt{12ax} dx-2\int_{4a}^{8a}\sqrt{\left(64a^{2}-x^{2}\right)} dx
=64{\pi}a^{2}-4\sqrt{3a}.\frac{2}{3}\left[x^{\frac{3}{2}}\right]_{0}^{4a}\\-2\left[\frac{x}{2}\sqrt{\left(64a^{2}-x^{2}\right)}+\frac{64a^{2}}{2}.\sin^{-1}\left(\frac{x}{8a}\right)\right]_{4a}^{8a}

=64{\pi}a^{2}-\frac{64\sqrt{3}}{3}a^{2}\\-2\left[32a^{2}\sin^{-1}\left(1\right)-2a.4\sqrt{3}a-32a^{2}\sin^{-1}\left(\frac{1}{2}\right)\right]
=64{\pi}a^{2}-\frac{64\sqrt{3}}{3}a^{2}-32{\pi}a^{2}+16\sqrt{3}a^{2}+\left(\frac{32}{3}\right){\pi}a^{2}
\frac{16}{3}a^{2}\left(8{\pi}-\sqrt{3}\right)
उपर्युक्त उदाहरणों के द्वारा समाकलन गणित में क्षेत्रकलन (Quadrature in Integral Calculus),समाकलन गणित में क्षेत्रकलन विधि (Quadrature Method in Integral Calculus) को समझ सकते हैं।

Also Read This Article:Surface Area of Solid of Revolution

3.समाकलन गणित में क्षेत्रकलन (Quadrature in Integral Calculus),समाकलन गणित में क्षेत्रकलन विधि (Quadrature Method in Integral Calculus) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:

• उपर्युक्त प्रश्नों के उत्तर द्वारा समाकलन गणित में क्षेत्रकलन (Quadrature in Integral Calculus),समाकलन गणित में क्षेत्रकलन विधि (Quadrature Method in Integral Calculus) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।

Quadrature in Integral Calculus

समाकलन गणित में क्षेत्रकलन
(Quadrature in Integral Calculus)

Quadrature in Integral Calculus

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Instagram	click here
4.	Linkedin	click here
5.	Facebook Page	click here
6.	Twitter	click here