Pythagoras Theorem Class 10

Mathematics Satyam April 9, 2023 10th Mathematics No Comments

Contents hide

1 1.पाइथागोरस प्रमेय कक्षा 10 (Pythagoras Theorem Class 10),पाइथागोरस प्रमेय (Pythagoras Theorem):

1.1 2.पाइथागोरस प्रमेय कक्षा 10 पर आधारित उदाहरण (Examples Based on Pythagoras Theorem Class 10):

1.2 3.पाइथागोरस प्रमेय कक्षा 10 की समस्याएँ (Pythagoras Theorem Class 10 Problems):

1.2.1 4.पाइथागोरस प्रमेय कक्षा 10 (Frequently Asked Questions Related to Pythagoras Theorem Class 10),पाइथागोरस प्रमेय (Pythagoras Theorem) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:

1.2.2 प्रश्न:1.समरूप आकृतियों और सर्वांगसम आकृतियों में क्या अन्तर है? (What is the Difference Between Similar and Congruent Figures?):

1.2.3 प्रश्न:2.समरूप आकृतियाँ किसे कहते हैं? (What are Similar Figures?):

1.2.4 प्रश्न:3.सर्वांगसम आकृतियाँ किसे कहते हैं? (What are the Congruent Figures?):

1.2.4.1 Pythagoras Theorem Class 10

2 पाइथागोरस प्रमेय कक्षा 10 (Pythagoras Theorem Class 10)

2.1 Pythagoras Theorem Class 10

1.पाइथागोरस प्रमेय कक्षा 10 (Pythagoras Theorem Class 10),पाइथागोरस प्रमेय (Pythagoras Theorem):

Pythagoras Theorem Class 10

पाइथागोरस प्रमेय कक्षा 10 (Pythagoras Theorem Class 10) को बौधायन प्रमेय के नाम से भी जाना जाता है।इस आर्टिकल में पाइथागोरस प्रमेय और इस पर आधारित उदाहरणों के द्वारा इसको समझेंगे
प्रमेय (Theorem):6.7.यदि किसी समकोण त्रिभुज के समकोण वाले शीर्ष से कर्ण पर लम्ब डाला जाए तो इस लम्ब के दोनों ओर बने त्रिभुज सम्पूर्ण त्रिभुज के समरूप होते हैं तथा परस्पर भी समरूप होते हैं।
दिया है (Given):समकोण $\triangle ABC$ जिसमें $\angle B$ समकोण है।माना BD, कर्ण AC पर लम्ब है अर्थात् $BD \perp AC$

Pythagoras Theorem Class 10

सिद्ध करना है (To Prove):(i) $\triangle ADB \sim \triangle ABC$
(ii) $\triangle BDC \sim \triangle ABC$
(iii) $\triangle ADB \sim \triangle BDC$
उपपत्ति (Proof):(i) $\triangle ADB$ और $\triangle ABC$ में
$\angle A=\angle A$ (उभयनिष्ठ कोण है)
$\angle ADB=\angle ABC=90^{\circ}$ (दिया है)
AA समरूपता कसौटी से

$\triangle ADB \sim \triangle ABC$
(ii) $\triangle BDC$ तथा $\triangle ABC$ में
$\angle C=\angle C$ (उभयनिष्ठ कोण है)
$\angle B D C=\angle A B C=90^{\circ}$ (दिया है)
AA समरूपता कसौटी से

$\triangle BDC \sim \triangle ABC$
(iii) $\angle A+\angle ABD=90^{\circ} \cdots(1) \\ \angle ABD+\angle DBC=90 \cdots (2)$

(1) व (2) से
$\angle A+\angle ABD=\angle ABD+\angle DBC \\ \Rightarrow \angle A=\angle DBC \cdots(3) \\ \triangle ADB$ तथा $\triangle BDC$ में
$\angle A=\angle DBC$ [(3) से]
$\angle ADB=\angle BDC=90^{\circ}$ (दिया है)
AA समरूपता कसौटी से

$\triangle A D B \sim \triangle B D C$
प्रमेय (Theorem):6.8.एक समकोण त्रिभुज में कर्ण का वर्ग शेष दो भुजाओं के वर्गों के योग के बराबर होता है।
दिया है (Given):समकोण $\triangle ABC$ जिसका समकोण है।

Pythagoras Theorem Class 10

सिद्ध करना है (To Prove): $A C^2=A B^2+B C^2$
रचना (Construction): $B D \perp A C$ खींचा।
उपपत्ति (Proof): $\triangle A D B \sim \triangle A B C$ (प्रमेय 6.7 से)
अतः $\frac{A D}{A B}=\frac{A B}{A C}$ (भुजाएँ समानुपाती हैं)

$\Rightarrow AD \cdot AC=A B^2 \cdots(1)$
साथ ही $\triangle BDC \sim \triangle ABC$ (प्रमेय 6.7 से)

अतः $\frac{C D}{B C}=\frac{B C}{A C}$ (भुजाएँ समानुपाती हैं)

$\Rightarrow C D \cdot A C=B C^2 \cdots(2)$
(1) और (2) को जोड़ने परः

$AD \cdot A C+C D \cdot A C=A B^2+B C^2 \\ \Rightarrow A C(A D+C D)=A B^2+B C^2 \\ \Rightarrow A C \cdot A C=A B^2+B C^2 \\ \Rightarrow A C^2=A B^2+B C^2$
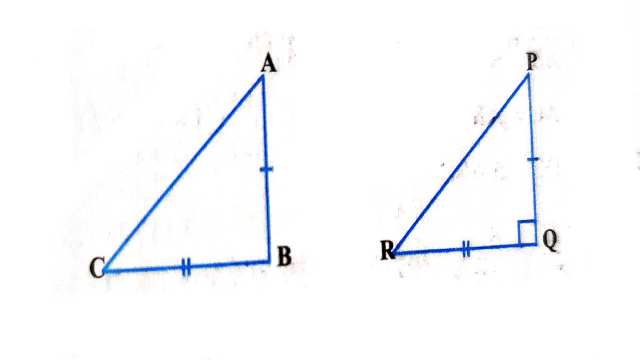
प्रमेय (Theorem):6.9.यदि किसी त्रिभुज की एक भुजा का वर्ग अन्य दो भुजाओं के वर्गों के योग के बराबर हो तो पहली भुजा का सम्मुख कोण समकोण होता है।
दिया है (Given): $\triangle A B C$ में $A C^2=A B^2+C^2$
सिद्ध करना है (To Prove): $\angle B=90^{\circ}$

Pythagoras Theorem Class 10

रचना (Construction): $\triangle P Q R$ की रचना इस प्रकार की कि $\angle Q=90^{\circ}$ और PQ=AB तथा QR=BC
उपपत्ति (Proof): $\triangle P Q R$ में
$P R^2=P Q^2+Q R^2$ (पाइथागोरस प्रमेय से क्योंकि)
परन्तु PQ=AB एवं QR=BC (रचना से)
$\Rightarrow P R^2=A B^2+B C^2 \cdots(1)\\ A C^2=A B^2+B C^2$ (दिया है)……(2)
(1) और (2) सेः
$P R^2=A C^2 \\ \Rightarrow P R=A C \\ \triangle A B C$ तथा $\triangle PQR$ में
PQ=AB (रचना से)
QR=BC (रचना से)
PR=AC [(3) में सिद्ध किया है]
SSS सर्वांगसमता कसौटी से

$\triangle A B C \cong \triangle P Q R \\ \angle B=\angle Q$ (CPCT)

$\angle Q=90^{\circ} \\ \Rightarrow B=90^{\circ}$
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:-Areas of Similar Triangles Class 10

2.पाइथागोरस प्रमेय कक्षा 10 पर आधारित उदाहरण (Examples Based on Pythagoras Theorem Class 10):

Example:1.कुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं।निर्धारित कीजिए कि इनमें से कौन-कौनसे त्रिभुज समकोण त्रिभुज हैं।इस स्थिति में कर्ण की लम्बाई भी लिखिए।
Example:1(i).7cm,24cm,25cm
Solution:7cm,24cm,25cm

$(7)^2+(24)^2 =49+576 \\ =625 \\ \Rightarrow(7)^2+(24)^2 =25^2$
अतः त्रिभुज समकोण त्रिभुज है तथा कर्ण की लम्बाई 25cm है।
Example:1(ii).3cm,8cm,6cm
Solution:3cm,8cm,6cm

$(3)^2+(6)^2 =9+36 \\ =45 \\ \Rightarrow(3)^2+(6)^2 =8^2$
अतः त्रिभुज समकोण त्रिभुज नहीं है।
Example:1(iii).50cm,80cm,100cm
Solution:50cm,80cm,100cm

$(50)^2+(80)^2 =2520+6400 \\ =8900 \\ \Rightarrow(50)^2+(80)^2 \neq(100)^2$
अतः त्रिभुज समकोण त्रिभुज नहीं है।
Example:1(iv).13cm,12cm,5cm
Solution:13cm,12cm,5cm

$(12)^2+(5)^2 =144+25 \\ =169 \\ \Rightarrow(12)^2+(5)^2 =(13)^2$
अतः त्रिभुज समकोण त्रिभुज है तथा कर्ण की लम्बाई 13cm है।
Example:2.PQR एक समकोण त्रिभुज है जिसका कोण P समकोण है तथा QR पर बिन्दु M इस प्रकार स्थित है कि $P M \perp Q R$ है।दर्शाइए कि $P M^2=Q M \cdot M R$ है।
Solution:दिया है (Given): $\triangle P Q R$ में $\angle P=90^{\circ}$ तथा $P M \perp Q R$
सिद्ध करना है (To Prove): $P M^2=Q M \cdot M R$
उपपत्ति (Proof): $\angle P=90^{\circ}$ (दिया है)
$\therefore \angle 1+\angle 2 =90^{\circ} \cdots (1) \\ \angle 1+\angle 3=90^{\circ} \cdots(2)\left[\triangle QPM \text{ में } \angle 5=\angle 6=90\right]$
समीकरण (1) व (2) सेः

$\angle 1+\angle 2=\angle 1+\angle 3 \\ \Rightarrow \angle 2=\angle 3 \cdots(3)$
अब $\triangle QPM$ और $\triangle PRM$ में
$\angle 2=\angle 3$ [(3) में सिद्ध किया है]
$\angle 5=\angle 6=90^{\circ}$ (दिया है)
AA समरूपता कसौटी से

$\triangle Q P M \sim \triangle PRM \\ \Rightarrow \frac{Q M}{P M} =\frac{P M}{M R}$ (भुजाएँ समानुपाती होती है)
$\Rightarrow P M^2 =Q M \cdot M R$
Example:3.आकृति में ABD एक समकोण त्रिभुज है जिसका कोण A समकोण है तथा $A C \perp B D$ है।दर्शाइए कि

(i) $AB^2=B C \cdot B D$
(ii) $AC^2=B C \cdot D C$
(iii) $AD^2=B D \cdot C D$

Pythagoras Theorem Class 10

Solution:दिया है (Given): $\triangle ABD$ में $\angle A=90^{\circ}$ तथा $AC \perp BD$
सिद्ध करना है (To Prove):(i) $A B^2=BC \cdot BD$
(ii) $A C^2=B C \cdot D C$
(iii) $A D^2=B D \cdot C D$
उपपत्ति (Proof):(i) $\triangle ACB$ तथा $\triangle DAB$ में
$\angle B=\angle B$ (उभयनिष्ठ है)
$\angle A C B=\angle D A B=90^{\circ}$ (दिया है)
AA समरूपता कसौटी से

$\triangle A C B \sim \triangle D A B$
$\frac{B C}{A B}=\frac{A B}{B D}$ (भुजाएँ समानुपाती हैं)
$\Rightarrow AB^2=BC \cdot BD$
(ii) $\triangle BAD$ में
$\angle A=90^{\circ} \\ \angle B A C+\angle D A C=90^{\circ} \cdots(1) \\ \triangle BAC$ में
$\angle B C A=90^{\circ} \\ \angle B+\angle B A C=90^{\circ} \cdots(2)$
(1) और (2) सेः

$\angle B A C+\angle D A C=\angle B+\angle B A C \\ \Rightarrow \angle D A C=\angle B \cdots(3) \\ \triangle D C A$ तथा $\triangle A C B$ में
$\angle D A C=\angle B$ [(3) में सिद्ध किया है]
$\angle D C A=\angle A C B=90^{\circ}$ (दिया है)
AA समरूपता कसौटी से

$\triangle D C A \sim \triangle A C B \\ \Rightarrow \frac{A C}{B C}=\frac{D C}{A C}$ (भुजाएँ समानुपाती होती है)

$\Rightarrow A C^2=BC\cdot DC$
(iii) $\triangle B A D$ तथा $\triangle A C D$ में
$\angle B A D=\angle A C D=90^{\circ}$ (दिया है)
$\angle D=\angle D$ (उभयनिष्ठ)
AA समरूपता कसौटी से
$\triangle B A D \sim \triangle A C D \\ \frac{A D}{C D}=\frac{B D}{A D}$ (भुजाएँ समानुपाती होती हैं)

$\Rightarrow A D^2=B D \cdot C D$
Example:4.ABC एक समद्विबाहु त्रिभुज है जिसका कोण C समकोण है।सिद्ध कीजिए कि $A B^2=2 A C^2$ है।

Pythagoras Theorem Class 10

Solution:दिया है (Given): $\triangle A B C$ एक समद्विबाहु त्रिभुज है तथा $\angle C=90^{\circ}$
सिद्ध करना है (To Prove): $A B^2=2 A C^2$
उपपत्ति (Proof): $\triangle A C B$ में $\angle C=90^{\circ}$
पाइथागोरस प्रमेय से

$A B^2 =A C^2+B C^2 \\ =AC^2+AC^2 \quad(\therefore B C=A C) \\ =2 AC^2 \\ \Rightarrow AB^2 =2 A C^2$
Example:5.ABC एक समद्विबाहु त्रिभुज है जिसमें AC=BC है।यदि $A B^2=2 A C^2$ है तो सिद्ध कीजिए कि ABC एक समकोण त्रिभुज है।
Solution:दिया है (Given): $\triangle A B C$ समद्विबाहु त्रिभुज है जिसमें AC=BC तथा $A B^2=2 A C^2$ है।
सिद्ध करना है (To Prove): $\triangle A B C$ समकोण त्रिभुज है।
उपपत्ति (Proof): $A B^2=2 A C^2$ (दिया है)

$\Rightarrow A B^2=A C^2+A C^2 \\ \Rightarrow A B^2=A C^2+B C^2\left(\because AC=BC\right )$
पाइथागोरस प्रमेय के विलोम से,
एक $\triangle A B C$ समकोण त्रिभुज है।
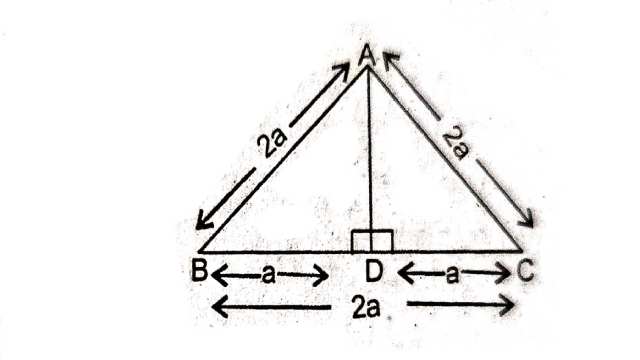
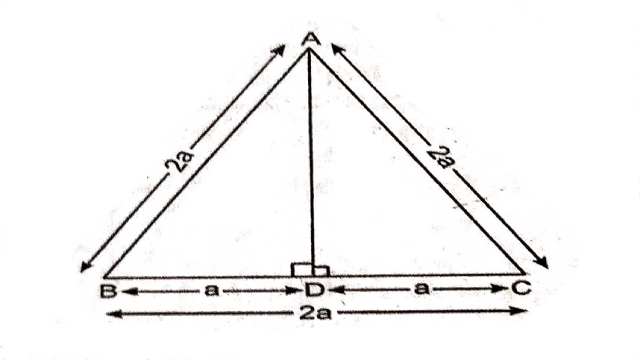
Example:6.एक समबाहु त्रिभुज ABC की भुजा 2a है।उसके प्रत्येक शीर्ष लम्ब की लम्बाई ज्ञात कीजिए।

Pythagoras Theorem Class 10

Solution: $\triangle A B C$ समबाहु त्रिभुज है जिसकी भुजा 2a है।

$A D \perp B C$
AB=AC=BC=2a

RHS सर्वागसमता से
$\triangle A D B \cong \triangle ADC$
BD=DC=a
अब समकोण $\triangle A D B$ में

$A B^2=A D^2+B D^2 \\ \Rightarrow(2 a)^2=A D^2+(a)^2 \\ \Rightarrow 4 a^2-a^2=A D^2 \\ \Rightarrow A D^2=3 a^2 \\ \Rightarrow A D=\sqrt{3} a$
Example:7.सिद्ध कीजिए कि एक समचतुर्भुज की भुजाओं के वर्गों का योग उसके विकर्णों के वर्गों के योग के बराबर होता है।

Pythagoras Theorem Class 10

Solution:दिया है (Given):समचतुर्भुज ABCD के विकर्ण AC और BD बिन्दु O पर प्रतिच्छेद करते हैं।
सिद्ध करना है (To Prove): $A B^2+B C^2+C D^2+D A^2=A D^2+B D^2$
उपपत्ति (Proof):समचतुर्भुज के विकर्ण समकोण पर समद्विभाजित करते हैं अतः समकोण $\triangle AOB$ में
$A B^2=O A^2+O B^2$ (पाइथागोरस प्रमेय से)

$\Rightarrow A B^2=\left(\frac{A C}{2}\right)^2+\left(\frac{B D}{2}\right)^2 \quad\left[\because A C=2 OA ,BD=2 OB\right] \\ \Rightarrow 4 A B^2=A C^2+B D^2 \\ A B^2+A B^2+A B^2+A B^2=A C^2+B D^2 \\ \Rightarrow A B^2+B C^2+C D^2+D A^2=A C^2+B D^2 \left[\because A B=BC =CD=DA\right]$
Example:8.आकृति में $\triangle A B C$ के अभ्यन्तर में स्थित कोई बिन्दु O है $O D \perp B C, OE \perp AC$ तथा $OF \perp AB$ और है।दर्शाइए कि

(i) $O A^2+O B^2+O C^2-O B^2-O E^2-O F^2=A F^2+B D^2+CE^{2}$
(ii) $A F^2+B D^2+C E^2=A E^2+C D^2+B F^2$

Pythagoras Theorem Class 10

Solution:दिया है (Given): $\triangle A B C$ में $OD \perp BC,OE \perp AC ,OF \perp A B$
सिद्ध करना है (To Prove):(i) $O A^2+O B^2+O C^2-O B^2-O E^2-O F^2=A F^2+B D^2+CE^{2}$
(ii) $A F^2+B D^2+C E^2=A E^2+C D^2+B F^2$
उपपत्ति (Proof):(i)समकोण $\triangle OAF$ में

$O A^2=A F^2+O F^2 \cdots(1)$
समकोण $\triangle O B D$ में

$B D^2+O D^2=O B^2 \\ O B^2=B D^2+O D^2 \cdots(2)$
समकोण $\triangle O C E$ में

$O C^2=C E^2+O E^2 \cdots(3)$
समीकरण (1),(2) व (3) को जोड़ने परः

$O A^2+O B^2+O C^2= A F^2+O F^2+B D^2+O D^2+C E^2+O E^2 \\ \Rightarrow O A^2+O B^2+O C^2-O D^2-O E^2-O F^2=A F^2+B D^2+C E^2 \cdots(4)$
(ii) समकोण $\triangle A O E$ में

$A E^2=O A^2=O E^2 \cdots(5)$
समकोण $\triangle OCD$ में

$C D^2=O C^2=O D^2 \cdots(6)$
समकोण $\triangle OBF$ में

$B F^2=O B^2-O F^2 \cdots(7)$

समीकरण (5),(6) व (7) को जोड़ने परः
$A E^2+C D^2+B F^2=O A^2+O C^2+O B^2-O E^2 -O D^2=O F^2 \cdots(8)$
(4) व (8) सेः

$A F^2+B D^2+C E^2=A E^2+C D^2+B F^2$
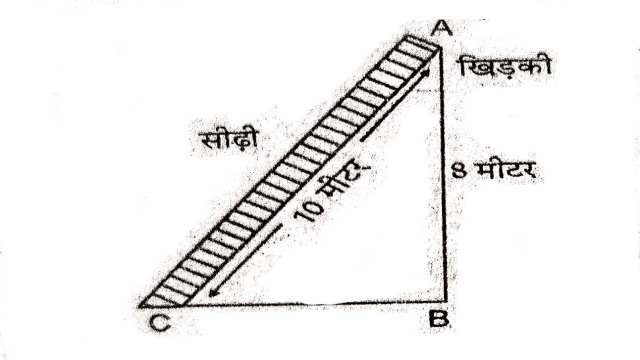
Example:9.10m लम्बी एक सीढ़ी एक दीवार पर टिकाने पर भूमि से 8m की ऊँचाई पर स्थित एक खिड़की तक पहुँचती है।दीवार के आधार से सीढ़ी के निचले सिरे की दूरी ज्ञात कीजिए।

Pythagoras Theorem Class 10

Solution:माना खिड़की की धरती से ऊँचाई (AB)=8 मीटर
सीढ़ी की लम्बाई (AC)=10 मीटर
सीढ़ी के निचले सिरे और दीवार के आधार के बीच की दूरी (BC)=?
$\triangle A B C$ में
$A C^2=A B^2+B C^2$ (पाइथागोरस प्रमेय से)

$(10)^2=(8)^2+B C^2 \\ \Rightarrow B C^2=100-64 \\ \Rightarrow B C^2=36 \\ \Rightarrow B C=\sqrt{36} \\ \Rightarrow B C=6 \text{मीटर}$
Example:10.18m ऊँचे एक उर्ध्वाधर खम्भे के ऊपरी सिरे से एक तार का एक सिरा जुड़ा हुआ है तथा तार का दूसरा सिरा एक खूँटे से जुड़ा हुआ है।खम्भे के आधार से खूँटे को कितनी दूरी पर गाड़ा जाए कि तार तना रहे जबकि तार की लम्बाई 24m है।

Pythagoras Theorem Class 10

Solution:माना खम्भे की ऊँचाई (AB)=18 मीटर
तार की लम्बाई (AC)=24 मीटर
खूँटे की स्थिति C है।इसकी खम्भे के आधार से दूरी (BC)=?
समकोण $\triangle A B C$ में,
$A C^2=A B^2+B C^2$ (पाइथागोरस प्रमेय से)
$\Rightarrow(24)^2 =(18)^2+(B C)^2 \\ \Rightarrow(B C)^2=(24)^2-(18)^2 \\ =576-324 \\ =252 \\ \Rightarrow BC =\sqrt{252} \\ \therefore BC=6 \sqrt{7}$ मीटर
Example:11.एक हवाई जहाज एक हवाई अड्डे से उत्तर की ओर 1000 km/hr की चाल से उड़ता है।इसी समय एक अन्य हवाई जहाज उसी हवाई अड्डे से पश्चिम की ओर 1200 km/hr की चाल से उड़ता है। $1 \frac{1}{2}$ घण्टे के बाद दोनों हवाई जहाजों के बीच दूरी कितनी होगी?

Pythagoras Theorem Class 10

Solution:पहले हवाई जहाज की चाल=1000 km/hr
दूरी=चाल×समय

= $1000 \times 1 \frac{1}{2} \\ =1000 \times \frac{3}{2} \\ =1500 \mathrm{~km}$
दूसरे हवाई जहाज की चाल=1200 km/hr
दूरी= $1200 \times \frac{3}{2} \\ =1800 \mathrm{km}$

समकोण $\triangle AOB$ मे पाइथागोरस प्रमेय से

$AB^2=O A^2+O B^2 \\ =(150)^2+(1800)^2 \\ =2250000+3240000 \\ =5490000 \\ \therefore A B =\sqrt{5490000} \\ \Rightarrow AB=300 \sqrt{6}$
Example:12.दो खम्भे जिनकी ऊँचाईयाँ 6m और 11m है तथा ये समतल भूमि पर खड़े हैं।यदि इनके निचले सिरों के बीच की दूरी 12m है तो इनके ऊपरी सिरों के बीच की दूरी ज्ञात कीजिए।

Pythagoras Theorem Class 10

Solution:एक खम्भे की ऊँचाई (AB)=11 मीटर
दूसरे खम्भे की ऊँचाई (CD)=6 मीटर
खम्भों के आधारों के बीच दूरी (BD)=12 मीटर
C से AB पर CE लम्ब खींचते है अर्थात् $CE \perp AB$
BE=OC=6 मीटर
AE=AB-BE=11-6 मीटर
AE=5 मीटर
तथा CE=BD=12 मीटर
समकोण $\triangle A E C$ में

$A C^2=A E^2+E C^2 \\ =(5)^2+(12)^2 \\ =25+144 \\ \Rightarrow A C^2 =169 \\ A C =\sqrt{169} \\ A C =13$ मीटर
Example:13.एक त्रिभुज ABC जिसका कोण C समकोण है,की भुजाओं CA और CB पर क्रमशः बिन्दु D और E स्थित हैं।सिद्ध कीजिए कि $A E^2+B D^2=A B^2+D E^2$ है।

Pythagoras Theorem Class 10

Solution:दिया है (Given): $\triangle ABC$ एक समकोण त्रिभुज है जिसमें $\angle C=90^{\circ}$ तथा भुजाओं CA और CB पर क्रमशः बिन्दु D और E स्थित हैं।
सिद्ध करना है (To Prove): $A E^2+B D^2=A B^2+D E^2$
उपपत्ति (Proof):समकोण $\triangle BCA$ में
पाइथागोरस प्रमेय से

$A B^2=B C^2+C A^2 \cdots(1)$
समकोण $\triangle C E D$ में
$D E^2=E C^2+D C^{2}$ (पाइथागोरस प्रमेय से)…….(2)
समीकरण (1) व (2) को जोड़ने परः

$A B^2+D E^2=B C^2+C A^2+E C^2+D C^2 \\ \Rightarrow A B^2+D E^2=\left(C A^2+E C^2\right)+\left(B C^2+D C^2\right) \cdots(3)$
समकोण $\triangle BCD$ में

$B D^2=B C^2+C D^2 \ldots(4)$
समकोण $\triangle ACE$ में

$A E^2=A C^2+C E^2 \cdots(5)$
समीकरण (4) व (5) को जोड़ने परः

$B D^2+A E^2=B C^2+C D^2+A C^2+C E^2 \cdots(6)$
समीकरण (5) व (6) सेः

$A E^2+B D^2=A B^2+D E^2$
Example:14.किसी त्रिभुज ABC के शीर्ष A से BC पर डाला गया लम्ब BC को बिन्दु D पर इस प्रकार प्रतिच्छेद करता है कि DB=3CD (देखिए आकृति)।सिद्ध कीजिए कि $2 A B^2=2 A C^2+B C^2$ है।

Pythagoras Theorem Class 10

Solution:दिया है (Given): $\triangle ABC$ में आधार BC पर शीर्ष A से AD लम्ब इस प्रकार डाला गया है कि BD=3CD
सिद्ध करना है (To Prove): $2 A B^2=2 A C^2+B C^2$
उपपत्ति (Proof):समकोण $\triangle ABD$ में

$A B^2=A D^2+B D^2 \cdots(1) \\ =A D^2+(B C-C D)^2 \\ =A D^2+C D^2+B C^2-2 B C \cdot C D \\ =\left(A D^2+C D^2\right)+B C^2-2 B C\left(\frac{B C}{4}\right) \\ \left [ \because BD=3 CD \text { अत } BC=4 C D \right ] \\ =\left(A D^2+C D^2\right)+B C^2-\left(\frac{ B C^2}{2}\right) \\ =A C^2+\frac{B C^2}{2}\left[\because A C^2=A D^2+C D^2\right] \\ =\frac{2 A C^2+B C^2}{2} \\ \Rightarrow 2 A B^2=A C^2+B C^2$
Example:15.किसी समबाहु त्रिभुज ABC की भुजा BC पर एक बिन्दु D इस प्रकार स्थित है कि $BD=\frac{1}{3} BC$ है।सिद्ध कीजिए कि $9 A D^2=7 A B^2$ है।

Pythagoras Theorem Class 10

Solution:दिया है (Given): $\triangle ABC$ समबाहु की भुजा BC पर बिन्दु D इस प्रकार स्थित है कि $BD=\frac{1}{3} BC$
सिद्ध करना है (To Prove): $9 A D^2=7 A B^2$
रचना (Constriction):A से BC पर $AE \perp BC$ खींचा।
उपपत्ति (Proof):समकोण $\triangle ABC$ में

$AB^2=B L^2+A L^2 \\ =(B D+D L)^2+A L^2 \\ =B D^2+2 B D \cdot DL+DL^2+A L^2 \\ =\left(\frac{B C}{3}\right)^2+2\left(\frac{B C}{3}\right) D L+A D^2 \\ \left[\because A D^2=D L^2+A L^2 \text { तथा } B D=\frac{1}{3} B C\right] \\ =\frac{B C^2}{9}+\frac{2 B C}{3}\left(\frac{B C}{6}\right)+A D^2 \\ \left[\because B D=\frac{1}{3} B C \text { तथा } B L=\frac{1}{2} BC \quad \therefore D L=\frac{1}{6} B C\right] \\ = \frac{B C^2}{9}+\frac{B C^2}{9}+A D^2 \\ =\frac{2 B C^2+A D^2}{9} \\ =\frac{9 A B^2}{9}+A D^2[\because A B=B C=A C] \\ \Rightarrow A B^2-\frac{2 A B^{2}}{9}=A D^2 \\ \Rightarrow 9 A B^2-2 A B^2=9 A D^2 \\ \Rightarrow 7 A B^2=9 A D^2$
Example:16.किसी समबाहु त्रिभुज में सिद्ध कीजिए कि उसकी एक भुजा के वर्ग का तिगुना उसके एक शीर्षलम्ब के वर्ग के चार गुने के बराबर होता है।

Pythagoras Theorem Class 10

Solution:दिया है (Given): $\triangle A B C$ समबाहु त्रिभुज है अर्थात् AB=BC=CA तथा $A D \perp B C$ है।
सिद्ध करना है (To Prove): $3 A B^2=4 A D^2$
उपपत्ति (Proof): $\triangle A B C$ में
AB=BC=CA

$A D \perp B C \\B D=D C=\frac{1}{2} B C$
समकोण $\triangle A B D$ में

$AB^2=A D^2+B D^2 \\ \Rightarrow AB^2=A D^2+\left(\frac{A B}{2}\right)^2 \\ \Rightarrow A B^2-\frac{A B^2}{4}=A D^2 \\ \Rightarrow 4 A B^2-A B^2=4 A D^2 \\ \Rightarrow 3 A B^2=4 A D^2$
Example:17.सही उत्तर चुनकर उसका औचित्य दीजिएः $\triangle ABC$ में, AB= $6 \sqrt{3}$ cm,AC=12cm और BC=6cm है।कोण B हैः
(A)120°(B)60° (C)90° (D)45°
Solution:AC=12सेमी,AB= $6 \sqrt{3}$ सेमी,BC=6सेमी

$\Rightarrow A B^2+B C^2=(6 \sqrt{3})^2+(6)^2 \\ =108+36 \\ =144 \\ =12^2 \\ \Rightarrow A B^2+B C^2=A C^2$
पाइथागोरस प्रमेय के विलोम से $\triangle ABC$ में $\angle B= 90°$
अतः सही विकल्प (C) है।
उपर्युक्त उदाहरणों के द्वारा पाइथागोरस प्रमेय कक्षा 10 (Pythagoras Theorem Class 10),पाइथागोरस प्रमेय (Pythagoras Theorem) को समझ सकते हैं।

3.पाइथागोरस प्रमेय कक्षा 10 की समस्याएँ (Pythagoras Theorem Class 10 Problems):

Pythagoras Theorem Class 10

(1.)एक समकोण $\triangle ABC$ में कोण C समकोण है,बिन्दु D भुजा BC का मध्य बिन्दु है।सिद्ध कीजिए किः $B C^2=4\left(A D^2-A C^2\right)$ ।
(2.)किसी समद्विबाहु त्रिभुज ABC में AB=AC है तथा शीर्ष B से सम्मुख भुजा AC पर लम्ब BD खींचा गया है।सिद्ध कीजिए कि

$B D^2-C D^2=2 A D \cdot DC$
उपर्युक्त सवालों को हल करने पर पाइथागोरस प्रमेय कक्षा 10 (Pythagoras Theorem Class 10),पाइथागोरस प्रमेय (Pythagoras Theorem) को ठीक से समझ सकते हैं।

Also Read This Article:-Similarity of Triangles Class 10

4.पाइथागोरस प्रमेय कक्षा 10 (Frequently Asked Questions Related to Pythagoras Theorem Class 10),पाइथागोरस प्रमेय (Pythagoras Theorem) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:

प्रश्न:1.समरूप आकृतियों और सर्वांगसम आकृतियों में क्या अन्तर है? (What is the Difference Between Similar and Congruent Figures?):

उत्तर:सभी सर्वांगसम आकृतियाँ समरूप होती है परन्तु समरूप आकृतियों का सर्वांगसम होना आवश्यक नहीं है।

प्रश्न:2.समरूप आकृतियाँ किसे कहते हैं? (What are Similar Figures?):

उत्तर:ऐसी ज्यामितीय आकृतियाँ जिनका रूप (Shape) बिल्कुल समान हो,समरूप आकृतियाँ कहलाती हैं।

प्रश्न:3.सर्वांगसम आकृतियाँ किसे कहते हैं? (What are the Congruent Figures?):

उत्तर:ऐसी आकृतियाँ जिनके आकार (shape) व आमाप (size) बिल्कुल एक समान हों अर्थात् परस्पर अध्यारोपण से एक-दूसरे को पूरा-पूरा ढक लें, सर्वांगसम आकृतियाँ कहलाती है।
उपर्युक्त प्रश्नों के उत्तर द्वारा पाइथागोरस प्रमेय कक्षा 10 (Pythagoras Theorem Class 10),पाइथागोरस प्रमेय (Pythagoras Theorem) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Instagram	click here
4.	Linkedin	click here
5.	Facebook Page	click here
6.	Twitter	click here

Pythagoras Theorem Class 10

पाइथागोरस प्रमेय कक्षा 10
(Pythagoras Theorem Class 10)

Pythagoras Theorem Class 10

पाइथागोरस प्रमेय कक्षा 10 (Pythagoras Theorem Class 10) को बौधायन प्रमेय के नाम
से भी जाना जाता है।इस आर्टिकल में पाइथागोरस प्रमेय और इस पर आधारित उदाहरणों के
द्वारा इसको समझेंगे

About Author

Satyam

About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.