1.त्रिभुजों के गुणधर्म कक्षा 9 (Properties of Triangles class 9)-

त्रिभुजों के गुणधर्म कक्षा 9 (Properties of Triangles class 9) में त्रिभुज की सर्वांगसमता का प्रयोग करके समद्विबाहु त्रिभुज सम्बन्धित प्रमेयों एवं त्रिभुज की सर्वांगसमता की शेष प्रमेयों को सिद्ध करने के लिए करेंगे।
(1.)समद्विबाहु त्रिभुज (Isoscecles Triangle)-
एक त्रिभुज समद्विबाहु त्रिभुज कहलाता है यदि इसकी दो भुजाएं समान हों।
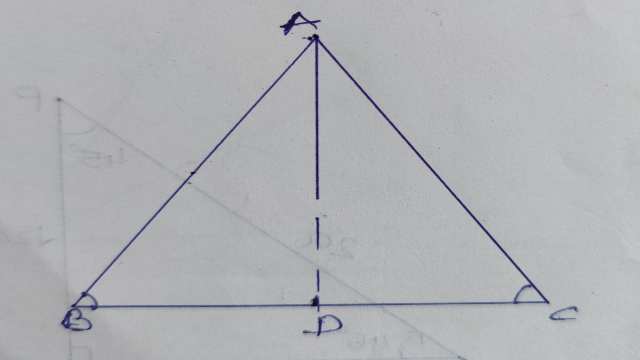
प्रमेय (Theorem) 1: यदि किसी त्रिभुज की दो भुजाएं बराबर हों तो उनके सम्मुख कोण भी बराबर होते हैं।
या
एक समद्विबाहु त्रिभुज की समान भुजाओं के सम्मुख कोण समान होते हैं।

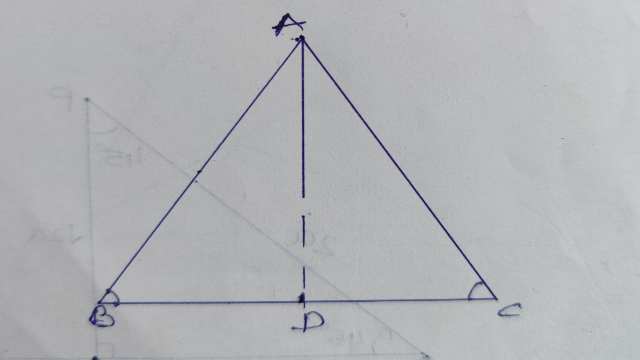
दिया है (Given):\Delta ABC एक समद्विबाहु त्रिभुज है जहां AB=BC है।
सिद्ध करना है (To Prove): \angle B=\angle C
रचना (Construction):\angle A का अर्धक AD खींचा जो BC को D पर मिलता है।
उपपत्ति (Proof): \Delta ABD एवं \Delta ACD में
AB=AC (दिया है)
\angle BAD=\angle CAD (रचना से)
AD=AD (उभयनिष्ठ भुजा)
भुजा-कोण-भुजा गुणधर्म से

\Delta ABD \cong  \Delta ACD
अतः संगत कोण

\angle B=\angle C
(सर्वांगसम त्रिभुजों के संगत कोण बराबर होते हैं)
प्रमेय (Theorem) 2:यदि किसी त्रिभुज में दो कोण बराबर हों तो उनकी सम्मुख भुजाएं भी बराबर होंगी।

दिया है (Given): \Delta ABC जिसमें \angle B=\angle C है।
सिद्ध करना है (To Prove):AB=AC
रचना (Construction):\angle BAC का समद्विभाजक AD खींचा।
उपपत्ति (Proof): \Delta ABD एवं \Delta ACD  में
\angle B=\angle C (दिया है)
AD=AD (उभयनिष्ठ भुजा)
\angle BAD=\angle CAD (रचना से)
कोण-भुजा-कोण गुणधर्म से

\Delta ABD \cong  \Delta ACD

अतः संगत भुजाएं AB=AC
(सर्वांगसम त्रिभुजों की संगत भुजाएं बराबर होती है)
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:-Surface Area of Cube and Cuboid

2.त्रिभुजों के गुणधर्म कक्षा 9 के उदाहरण (Properties of Triangles class 9 Examples)-

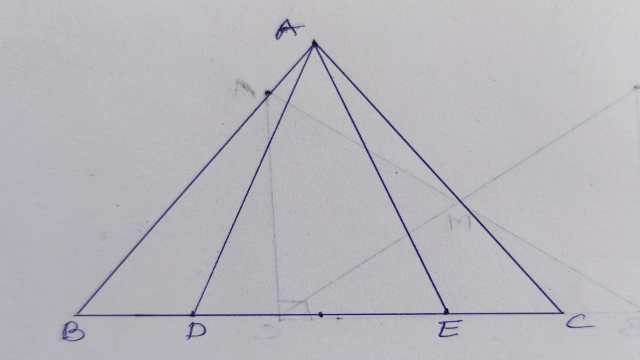
Example-1.चित्र में AD=BD एवं \angle C=\angle E हो तो सिद्ध कीजिए BC=AE

Solution- दिया है (Given): AB=BD एवं \angle C=\angle E
सिद्ध करना है (To Prove):BC=AE
उपपत्ति (Proof): \Delta ABD में
AD=BD

\therefore  \angle DAB=\angle DBA …..(1)
(बराबर भुजाओं के सम्मुख कोण बराबर होते हैं)
\Delta AEB तथा \Delta BCA में
AB=AB (उभयनिष्ठ है)
\angle E= \angle C (दिया है)
\angle DBA=\angle DAB(सिद्ध किया है)
(अतः भुजा-कोण-कोण सर्वांगसमता गुणधर्म से)

\Delta AEB \cong  \Delta BCA
BC=AE
(सर्वांगसम त्रिभुजों की संगत भुजाएं बराबर होती है)
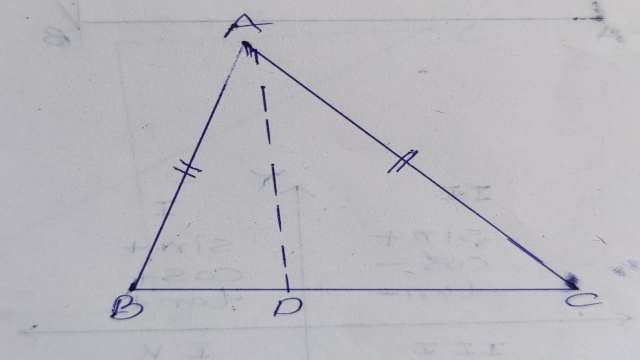
Example-2.यदि एक समद्विबाहु त्रिभुज ABC की माध्यमिका AD हो तथा \angle A=120^{\circ} एवं AB=AC हो तो का मान ज्ञात कीजिए।

Solution–\Delta ABD तथा \Delta ACD में
AB=AC (दिया है)
BD=DC (AD माध्यमिका है)
AD=AD (उभयनिष्ठ भुजा है)
(अतः भुजा-भुजा-भुजा सर्वांगसमता गुणधर्म से)

\Delta ABD \cong  \Delta ACD
\angle ADB=\angle ADC (सर्वांगसम त्रिभुजों के संगत कोण बराबर होते हैं)…..(1)
\angle ADB+\angle ADC =180^{\circ} (रैखिक कोण युग्म से)….(2)
(1) व (2) से-

\angle ADB=90^{\circ}
Example-3.चित्र में AB=ACएवं BE=CD हो तो सिद्ध कीजिए AD=AE.

Solution- दिया है (Given):AB=AC एवं BE=CD
सिद्ध करना है (To Prove): AD=AE

उपपत्ति (Proof):\Delta ABC में
AB=AC

\angle B=\angle C …..(1)
(बराबर भुजाओं के सम्मुख कोण बराबर होते हैं)
\Delta ABE तथा \Delta ACD में
AB=AC (दिया है)
\angle B=\angle C [(1) से]
BE=CD (दिया है)
(भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से)

\Delta ABE \cong  \Delta ACD

AD=AE

(सर्वांगसम त्रिभुजों की संगत भुजाएं बराबर होती है)
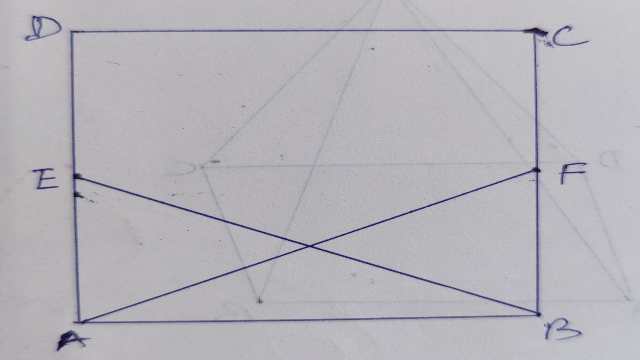
Example-4.एक वर्ग ABCD की भुजाओं AD एवं BC पर क्रमशः E एवं F दो बिन्दु इस प्रकार हैं कि AF=BE तो सिद्ध कीजिए कि (i)\angle BAF=\angle ABE
(ii)BF=AE

Solution- दिया है (Given):वर्ग ABCD में AF=BE
सिद्ध करना है (To Prove):(i)\angle BAF=\angle ABE

(ii) BF=AE
उपपत्ति (Proof): \Delta BAE तथा \Delta ABF
AB=AB (उभनिष्ठ भुजा है)
BE=AF (दिया है)

\angle A=\angle B=90^{\circ}
(अतः समकोण-कर्ण-भुजा सर्वांगसमता गुणधर्म से)

\Delta BAE \cong \Delta ABF

\angle BAF=\angle ABE
तथा BF=AE
(सर्वांगसम त्रिभुजों के संगत अवयव बराबर होते हैं)
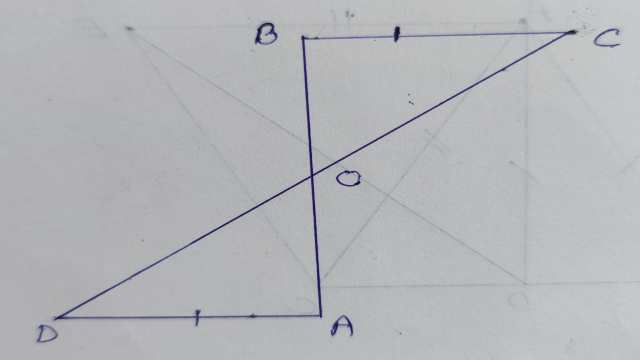
Example-5.एक रेखाखण्ड AB पर AD और BC दो बराबर लम्ब रेखाखण्ड हैं।दर्शाइए कि CD,रेखाखण्ड AB को समद्विभाजित करता है।

Solution- दिया है (Given): BC \perp  AB तथा AD \perp  AB तथा BC=AD
सिद्ध करना है (To Prove): OB=OA
उपपत्ति (Proof): \Delta AOD तथा \Delta BOC में
AD=BC (दिया है)
\angle DAO=\angle CBO =90^{\circ} (दिया है)
\angle AOD=\angle BOC (सम्मुख कोण)
(अतः भुजा-कोण-कोण सर्वांगसमता गुणधर्म से)

\Delta AOD \cong \Delta BOC
OB=OA
(सर्वांगसम त्रिभुजों की संगत भुजाएं बराबर होती है)
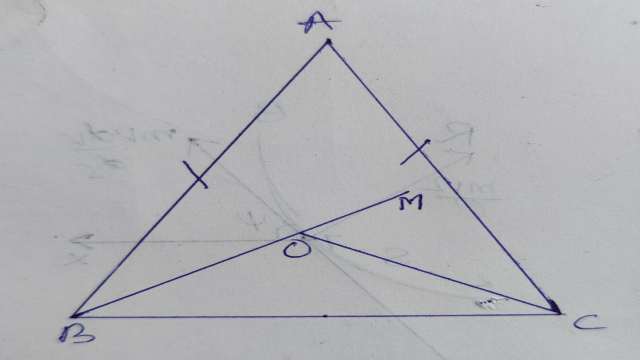
Example-6. AB=AC वाले एक समद्विबाहु त्रिभुज के कोणों B और C के समद्विभाजक परस्पर O पर प्रतिच्छेद करते हैं।BO को एक बिन्दु M तक बढ़ाया जाता है। सिद्ध कीजिए \angle MOC=\angle ABC है।

Solution- दिया है (Given): समद्विबाहु त्रिभुज ABC में AB=AC
सिद्ध करना है (To Prove):\angle MOC=\angle ABC
उपपत्ति (Proof): AB=AC
अतः \angle ABC=\angle ACB (बराबर भुजाओं के सम्मुख कोण बराबर होते हैं)

\frac{1}{2} \angle ABC=\frac{1}{2} \angle ACB \\  \angle OBC=\angle OCB....(1) \\ \angle MOC=\angle OBC+ \angle OCB….(2)
(किसी त्रिभुज का बहिष्कोण अन्तराभिमुख कोणों के योग के बराबर होता है)

(1) व (2) से-

\angle MOC=\angle OBC+ \angle OBC \\ \angle MOC=2 \angle OBC \\ \angle MOC=\angle ABC[ \because  \angle ABC=2 \angle OBC]
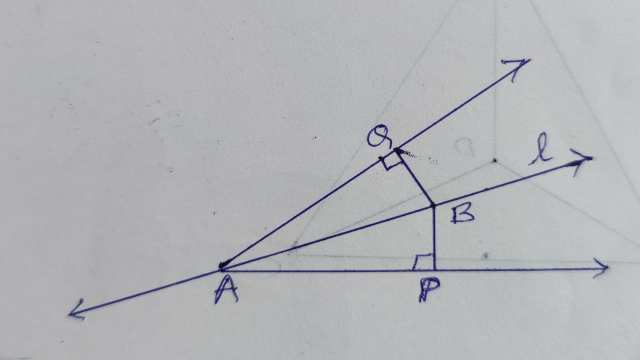
Example-7. रेखा l कोण A को समद्विभाजित करती है और B रेखा l पर स्थित कोई बिन्दु है।BP और BQ कोण A की भुजाओं पर B से डाले गए लम्ब हैं दर्शाइए कि

(i)\Delta APB \cong \Delta AQB
(ii)BO=BQ है अर्थात् बिन्दु B कोण की भुजाओं से समदूरस्थ है।

Solution- दिया है (Given): \angle QAB=\angle PAB तथा \angle AQB=\angle APB=90^{\circ}
सिद्ध करना है (To Prove):(i)\Delta APB \cong \Delta AQB
(ii)BO=BQ है अर्थात् बिन्दु B कोण की भुजाओं से समदूरस्थ है।
उपपत्ति (Proof):\Delta BAQ तथा  \Delta BAP में
AB=AB (उभयनिष्ठ भुजा है)
\angle QAB=\angle PAB (दिया है)
\angle AQB=\angle APB=90^{\circ}(दिया है)
(अतः भुजा-कोण-कोण सर्वांगसमता गुणधर्म से)

\Delta BAQ \cong  \Delta BAP
BP=BQ, अर्थात् बिन्दु B कोण की भुजाओं से समदूरस्थ है।
(सर्वांगसम त्रिभुजों की संगत भुजाएं बराबर होती है)
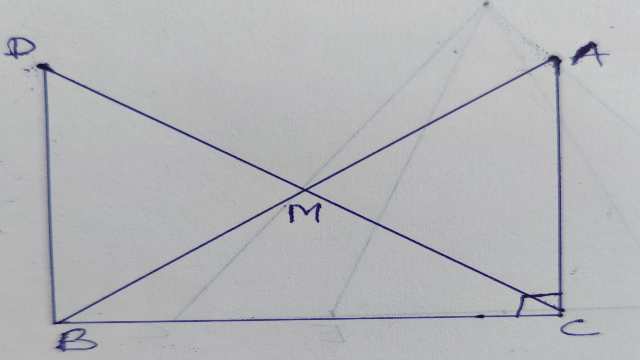
Example-8. एक समकोण त्रिभुज ABC में, जिसमें कोण C समकोण है,M कर्ण AB का मध्य-बिन्दु है।C को M से मिलाकर D तक इस प्रकार बढ़ाया गया है कि DM=CM है।बिन्दु D को बिन्दु B से मिला दिया जाता है।दर्शाइए कि(i)\Delta AMC \cong  \Delta BMD
(ii)\angle DBC एक समकोण है (iii) \Delta DBC \cong  \Delta ACB (iv) CM =\frac{1}{2} AB

Solution- दिया है (Given):\Delta ABC में \angle C=90^{\circ},AM=BM तथा DM=CM
सिद्ध करना है (To Prove):(i)\Delta AMC \cong  \Delta BMD

(ii) \angle DBC एक समकोण है (iii) \Delta DBC \cong  \Delta ACB (iv) CM =\frac{1}{2} AB
उपपत्ति (Proof): \Delta AMC तथा \Delta BMD में
AM=MB (दिया है)
CM=MD (दिया है)
\angle AMC=\angle BMD (शीर्षाभिमुख कोण)
(अतः भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से)

\Delta AMC \cong  \Delta BMD.....(1)
(iii) (1)के दोनों पक्षों में \Delta BMC जोड़ने पर

\Delta AMC + \Delta BMC \cong  \Delta BMD +\Delta BMC \\ \Delta DBC \cong  \Delta ACB

(ii)\angle C=\angle B=90^{\circ}

(सर्वांगसम त्रिभुजों के संगत कोण बराबर होते हैं)
(iv)\Delta DBC \cong  \Delta ACB \\ \angle MBC=\angle MCB

(सर्वांगसम त्रिभुजों के संगत कोण बराबर होते हैं)
BM=MC

\therefore  CM =\frac{1}{2} AB
(बराबर कोण की सम्मुख भुजाएं बराबर होती हैं)
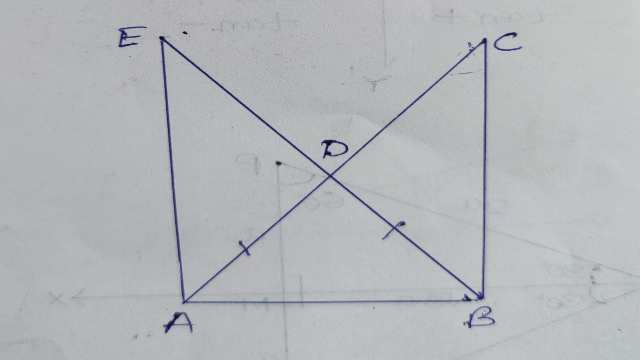
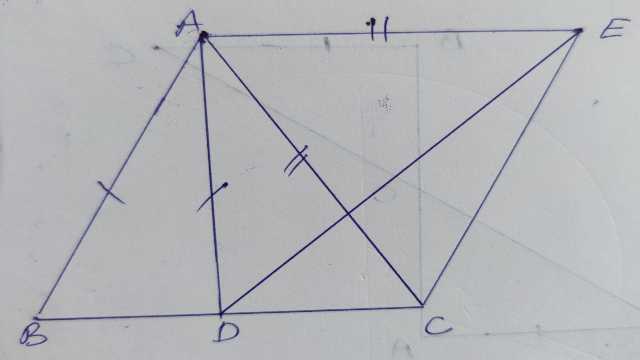
Example-9.चित्र में AC=AE,AB=AD और \angle BAD=\angle EAC है।दर्शाइए कि BC=DE है।

Solution- दिया है (Given):AC=AE,AB=AD और \angle BAD=\angle EAC
सिद्ध करना है (To Prove):\angle BAD=\angle EAC
दोनों पक्षों में \angle DAC जोड़ने पर

\angle BAD + \angle DAC=\angle EAC + \angle DAC \\  \Rightarrow \angle BAC=\angle EAD ....(1)
\Delta BAC तथा \Delta DAE  में
AC=AE (दिया है)
\angle BAC=\angle EAD [(1) से]
AB=AD (दिया है)
(अतः भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से)

\Delta BAC \cong  \Delta DAE
BC=AD (सर्वांगसम त्रिभुजों की संगत भुजाएं बराबर होती है)

3.त्रिभुजों के गुणधर्म कक्षा 9 की समस्याएं (Properties of Triangles class 9 Problems)-

(1.) \Delta ABC में \angle A का समद्विभाजक AD भुजा BC पर लम्ब है।दर्शाइए \Delta ABC एक समद्विबाहु त्रिभुज है।
(2.) सिद्ध कीजिए कि समद्विबाहु त्रिभुज की समान भुजाओं को समद्विभाजित करने वाली माध्यिकाएं समान होती है।
(3.)एक समद्विबाहु त्रिभुज ABC में AB=AC हो एवं भुजा BC,AC एवं AB के मध्य बिन्दु क्रमश: D,E,F हो तो सिद्ध कीजिए कि DE=DF
(4.)यदि एक त्रिभुज की एक भुजा के मध्य बिन्दु से दूसरी दो भुजाओं पर डाले गए लम्ब समान हो तो सिद्ध कीजिए कि त्रिभुज समद्विबाहु होगा।
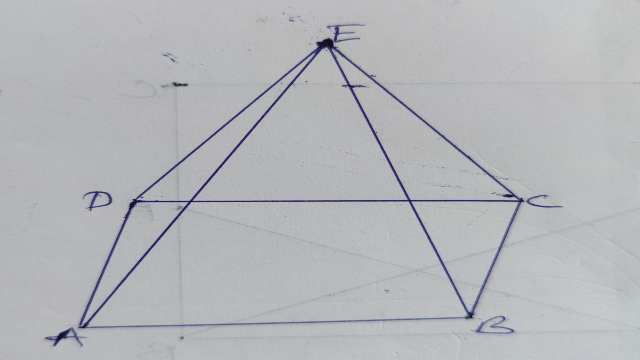
(5.)चित्र के अनुसार ABCD एक वर्ग है तथा \Delta CDE एक समबाहु त्रिभुज हो तो सिद्ध कीजिए कि AB=BE

(6.)चित्र में AB=AC है एवं \Delta ABC में D एक ऐसा बिन्दु है कि\angle DBC=\angle DCB सिद्ध कीजिए कि \angle BAC को AD समद्विभाजित करता है।

4.त्रिभुज के 5 गुणधर्म क्या हैं? (What are the 5 properties of a triangle?),त्रिभुज के गुणधर्म (Properties of Triangles)-

एक त्रिभुज की तीन भुजाएँ,तीन शीर्ष और तीन कोण होते हैं।
त्रिभुज के तीन आंतरिक कोणों का योग हमेशा 180°होता है।
त्रिभुज की दो भुजाओं की लंबाई का योग हमेशा तीसरी भुजा की लंबाई से अधिक होता है।
P,Q और R के साथ एक त्रिभुज को △PQR के रूप में दर्शाया जाता है।

5.छह प्रकार के त्रिभुज और उनके गुणधर्म क्या हैं? (What are the six types of triangles and their properties?)-

भुजाओं के आधार पर त्रिभुज के प्रकार-
स्कैलीन ट्राइंगल (Scalene Triangle)-यह विषमबाहु त्रिभुज होता है जिसकी तीनों भुजाएं असमान होती है।
आइसोसेलस ट्राइंगल (Isosceles Triangle)-यह समद्विबाहु त्रिभुज होता है जिसकी दो भुजाएं तथा दो कोण बराबर होती है।
इक्विनेंटल ट्रायंगल (Equilateral Triangle)-यह समबाहु त्रिभुज होता है जिसकी तीन भुजाएं तथा तीनों कोण बराबर होते हैं।प्रत्येक कोण 60° का होता है।
एंगल्स के आधार पर त्रिभुज के प्रकार-
एक्यूट ट्राइएंगल (Acute Triangle)-इसे न्यून कोण त्रिभुज कहा जाता है जिसका प्रत्येक कोण 90° से कम होता है अर्थात् प्रत्येक कोण न्यून कोण होता है।
ऑबट्यूज ट्राइएंगल (Obtuse Triangle)-इसे अधिक कोण त्रिभुज कहा जाता है जिसका एक कोण अधिक कोण अर्थात 90° से अधिक तथा 180° से कम होता है।
राइट ट्रायंगल (Right Triangle)-इसे समकोण त्रिभुज कहा जाता है जिसका एक कोण समकोण अर्थात् 90° का होता।इसमें कर्ण का वर्ग,शेष दो भुजाओं के वर्गो के योग के बराबर होता है।

6.विशेष समकोण त्रिभुज के गुणधर्म क्या हैं? (What are the properties of special right triangles?)-

एक विशेष समकोण त्रिभुज कुछ नियमित विशेषता के साथ एक समकोण त्रिभुज है जो त्रिभुज पर गणना को आसान बनाता है या जिसके लिए सरल सूत्र मौजूद हैं। उदाहरण के लिए एक समकोण त्रिभुज में कोण हो सकते हैं जो सरल संबंध बनाते हैं, जैसे कि 45°,45°,90°।इसे एक “कोण-आधारित” समकोण त्रिभुज कहा जाता है।

7.त्रिकोण के प्रकार क्या हैं और उनके गुणधर्मों को लिखो? (What are the types of triangles and write down their properties?)-

समद्विबाहु त्रिभुज: इसके दो बराबर भुजाएँ हैं।साथ ही, इन समान भुजाओं के विपरीत कोण समान हैं।समबाहु त्रिभुज: सभी भुजाएँ समान हैं और सभी तीन कोण 60° के बराबर हैं।एक्यूट एंगल्ड ट्रायंगल: एक त्रिभुज जिसके सभी कोण 90° से कम होते हैं।

8.त्रिभुज के कोण गुणधर्म (Angle Properties of Triangles)-

त्रिभुज के सभी आंतरिक कोणों का योग हमेशा 180° के बराबर होता है। इसे त्रिभुज का कोण योग गुणधर्म कहा जाता है।त्रिभुज के किन्हीं दो भुजाओं की लंबाई का योग तीसरी भुजा की लंबाई से अधिक है।त्रिभुज का कोई भी बाह्य कोण इसके अन्तराभिमुख कोणों के योग के बराबर होता है।

9.त्रिभुज सूत्र के गुणधर्म (Properties of Triangle Formula)-

1.त्रिभुज ABC के कोणों को A, B, C और इसकी विपरीत भुजाओं a, b, c द्वारा निरूपित किया जाता है।
2.s त्रिभुज ABC की अर्ध-परिधि को दर्शाता है,डेल्टा इसका क्षेत्रफल और R त्रिभुज ABC की परिधि है जो त्रिभुज ABC की परिधि है अर्थात R,परिधि-त्रिज्या है।
3.a/sinA=b/sinB = c/sinC =2R।
4.(i) a = b cos C + c cos B;
(ii) b = c cos A + a cos C,और
(iii) c = a cos B + b cos A

10.त्रिभुज के गुणधर्म कक्षा 9 (Properties of Triangle class 9)-

त्रिभुज के गुण हैं:
एक त्रिभुज के सभी कोणों का योग (सभी प्रकार का) 180° के बराबर है।
किसी त्रिभुज की दो भुजाओं की लंबाई का योग तीसरी भुजा की लंबाई से अधिक है।
उसी तरह, त्रिभुज के दोनों भुजाओं के बीच का अंतर तीसरी भुजा की लंबाई से कम होता है।

Also Read This Article:-Trigonometric Ratios of Acute Angle

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Instagram	click here
4.	Linkedin	click here
5.	Facebook Page	click here