1.गतिविज्ञान में जड़त्व गुणन (Product of Inertia in Dynamics),जड़त्व-आघूर्ण (Moment of Inertia):

Product of Inertia in Dynamics

गतिविज्ञान में जड़त्व गुणन (Product of Inertia in Dynamics) के इस आर्टिकल में किसी पिण्ड का किसी रेखा अथवा दो लम्ब निर्देशाक्ष के सापेक्ष जड़त्व गुणनफल ज्ञात करना सीखेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:- Apsidal in Dynamics

2.गतिविज्ञान में जड़त्व गुणन के उदाहरण (Product of Inertia in Dynamics Examples):

Example:8.प्रदर्शित करो कि निम्न प्रत्येक स्थिति में जड़त्व गुणन शून्य है:
(i)वृत्ताकार तार का इसके दो लम्बवत व्यासों के सापेक्ष,
(ii)दीर्घवृत्तीय चकती का दीर्घ एवं लघु अक्ष के सापेक्ष,
(iii)वृत्ताकार चकती का तल में केन्द्र से गुजरने वाली दो लम्बवत अक्षों के सापेक्ष।
(Prove that the product of inertia in the following case vanishes:
(i)circular wire about its two perpendicular diameters,
(ii)elliptic disc about major and minor axes,
(iii)circular disc about two perpendicular axes in its plane through the centre.)
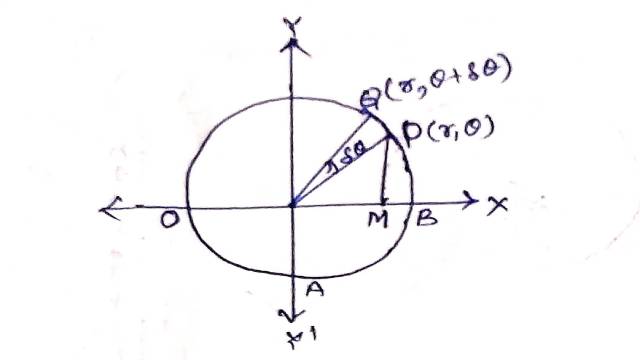
Solution:8(i).मान लो दिया हुआ वृत्ताकार तार OABPQO है जिसके दो लम्बवत व्यास OB व TA है तथा OB=TA=2r है।वृत्त के केन्द्र को ध्रुव लेने पर P के निर्देशांक (r,\theta) हों,तो अवयव चाप PQ=r \delta \theta
तार की परिधि=2 \pi r
तथा तार का घनत्व \rho=\frac{M}{2 \pi r}
जहाँ M वृत्ताकार तार की संहति है।

Product of Inertia in Dynamics

तार के अवयव की OB से दूरी=PM=r \sin \theta
तथा तार के अवयव की TA से दूरी=PL=r \cos \theta
तार के अवयव का OB तथा TA के परितः जड़त्व-गुणनफल=\frac{M}{2 \pi r} \cdot r \delta \theta \left( r \sin \theta \right)(r \cos \theta)
वृत्ताकार तार का OB तथा TA के परितः जड़त्व गुणनफल=\int_0^\pi \frac{M}{2 \pi r} \cdot r \cdot(r \sin \theta)(r \cos \theta) d \theta \\ =\frac{M}{4 \pi} r^2 \int_0^\pi \sin 2 \theta d \theta \\=\frac{M r^2}{4 \pi}\left[-\frac{\cos 2 \theta}{2}\right]_0^\pi \\ =\frac{M r^2}{8 \pi}[-\cos 2 \pi+\cos 0] \\ =\frac{\pi r^2}{8 \pi}[-1+1] \\ =0
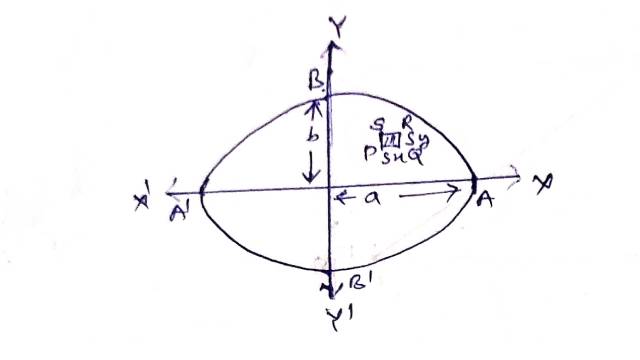
Solution:8(ii).माना दीर्घवृत्तीय चकती की संहति M है तथा दीर्घवृत्त के OA तथा OB दीर्घ व लघु अक्ष है और इसका समीकरण है:

Product of Inertia in Dynamics

दीर्घवृत्तीय चकती का एक अवयव \delta x \delta y का OA तथा OB के सापेक्ष जड़त्व-गुणन=(अवयव \delta x \delta y की संहति)x. y

=\frac{M}{\pi a b} \delta x \delta y \cdot x \cdot y
अतः दीर्घवृत्तीय चकती का OA व OB के सापेक्ष जड़त्व-गुणन
=\int_{-a}^a \int_{-\frac{b}{a}\sqrt{\left(a^2-x^2\right)}}^{\frac{b}{a} \sqrt{\left(a^2-x^2\right)}} \frac{M}{\pi a b} x y d x d y \\ =0 [विषम फलन है और विषम फलन का समाकलन शून्य होता है]
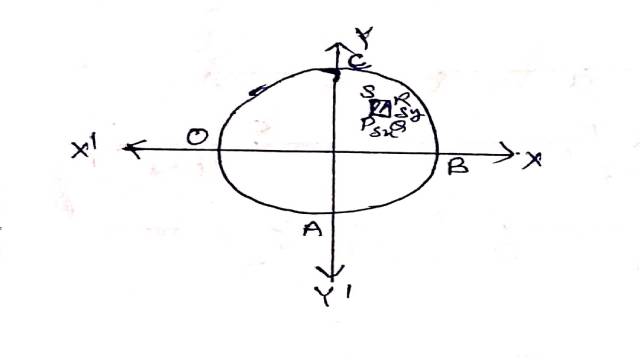
Solution:8(iii).मान लो कि दी हुई वृत्ताकार चकती OABC है जिसके केन्द्र से गुजरने वाले दो अक्ष OX तथा OY हों तो अवयव चाप PQRS=\delta x \delta y

Product of Inertia in Dynamics

तार की परिधि=2 \pi r
तथा तार का घनत्व \rho=\frac{M}{2 \pi r}
जहाँ वृत्ताकार तार की संहति M है।
तार के अवयव की OX से दूरी=y
तथा के अवयव की OY से दूरी=x
तार के अवयव का OX तथा OY के परितः जड़त्व गुणनफल =\frac{M}{2 \pi r} \delta x \delta y \cdot x \cdot y
वृत्ताकार तार का OX तथा OY के परितः जड़त्व गुणनफल=\int_{-a}^a \int_{-a}^a \frac{M}{2 \pi r} d x d y x \cdot y \\ =\frac{M}{2 \pi r} \int_{-a}^a \int_{-a}^a x y d x d y \\ =0 [विषम फलन का समाकलन शून्य होता है]
Example:9.एक समकोण त्रिभुज का,समकोण बनानेवाली भुजाओं 2a,2b के सापेक्ष जड़त्व गुणन ज्ञात करिए।
(Find the P. I. of a right angled triangle about side 2a,2b containing the right angle:)
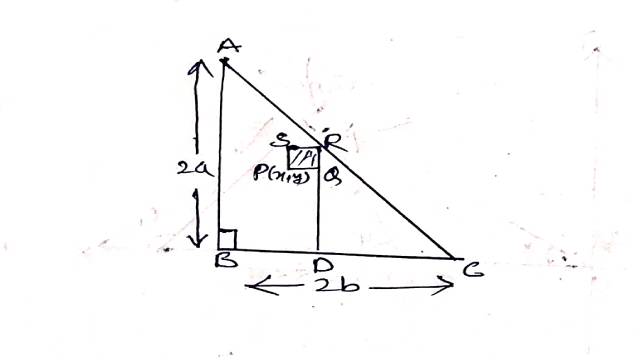
Solution:माना \triangle ABC जिसका कोण B समकोण है तथा AB=2a व BC=2b है।समकोण त्रिभुज के अवयव PQRS=\delta x \delta y
समकोण त्रिभुज का क्षेत्रफल =\frac{1}{2} \times 2 a \times 2 b \\ =2 a b
तथा समकोण त्रिभुज का घनत्व \rho=\frac{M}{2 a b}
जहाँ M समकोण त्रिभुज की संहति है।

Product of Inertia in Dynamics

त्रिभुज के अवयव की BC से दूरी=y
त्रिभुज के अवयव की AB से दूरी=x
त्रिभुज के अवयव का BC व AB के परितः जड़त्व-गुणन =\frac{M}{2 a b} \delta x \delta y \cdot x \cdot y \\ \triangle A B C \sim \triangle R D C \\ \frac{A B}{D R}=\frac{BC}{DC} \\ \frac{2 b}{y+s y}=\frac{2 a}{2 b-x-\delta x}  \\ \delta y व \delta x को नगण्य मानने पर

\Rightarrow \frac{2 a}{y}=\frac{2 b}{2 b-x} \\ \Rightarrow y=\frac{a}{b}(2 b-x) \cdots(1)
समकोण \triangle ABC का AB व BC के परितः जड़त्व-गुणन

=\int_0^{2 b} \int_0^y \frac{M}{2 a b} x y d x d y \\ =\frac{M }{2 a b} \int_{0}^{2b}\frac{x y^2}{2} d x \\ =\frac{M}{4 a b} \int_0^{2 b} \frac{x a^2}{b^2}(2 b-x)^2 d x \\ =\frac{M a}{4 b^3} \int_0^{2 b} x\left(4 b^2-4 b x+x^2\right) d x \\ =\frac{M a}{4 b^3} \int_0^{2 b}\left(4 b^2 x-4 b x^2+x^3\right) d x \\ =\frac{M a}{4 b^3}\left[2 b^2 x^2-\frac{4 b x^3}{3}+\frac{x^4}{4}\right]_0^{2 b} \\ =\frac{M a}{4 b^3} \left(8 b^4-\frac{32 b^4}{3}+4 b^4\right) \\ =\frac{M a}{4 b^3}\left[\frac{24 b^4-32 b^4+2 b^4}{3}\right] \\ =\frac{M a}{4 b^3} \times \frac{4 b^4}{3} \\ =\frac{M a b}{3}
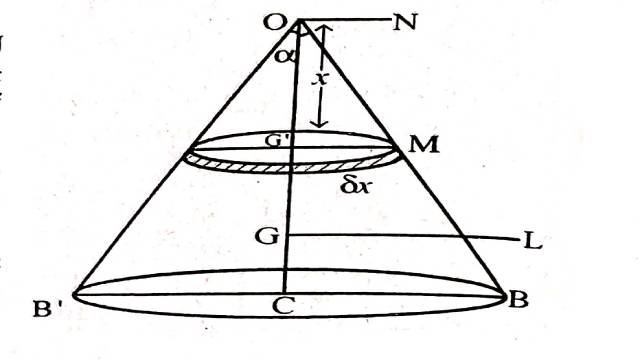
Example:10.एक लम्ब ठोस शंकु जिसकी ऊँचाई h तथा आधार की त्रिज्या a है,का इसकी अक्ष एवं शीर्ष से गुजरने वाली एक सरल रेखा जो इसकी अक्ष के लम्बवत है के सापेक्ष जड़त्व गुणन ज्ञात करिए।
(Find P. I. of a right circular cone whose height is h and radius of the base is a about its axis and a straight line through its vertex perpendicular to its axis)
Solution:माना कि शंकु OAB का अर्धशीर्ष कोण \alpha है।शंकु के शीर्ष O से x तथा x+\delta x दूरी वाले दो वृत्तीय काटों (circular sections) के बीच वाली एक वृत्तीय चक्रिका लो।यदि शंकु का घनत्व है,तो अवयव चक्रिका की संहति=\pi(x \tan \alpha)^2 \delta x \rho

Product of Inertia in Dynamics

अवयव चक्रिका का दोनों लम्बवत रेखाओं (OC,CN) के सापेक्ष जड़त्व-गुणन=\left(\pi \rho x^2 \tan ^2 \alpha \delta x\right) \cdot x \cdot 0 \\ =0
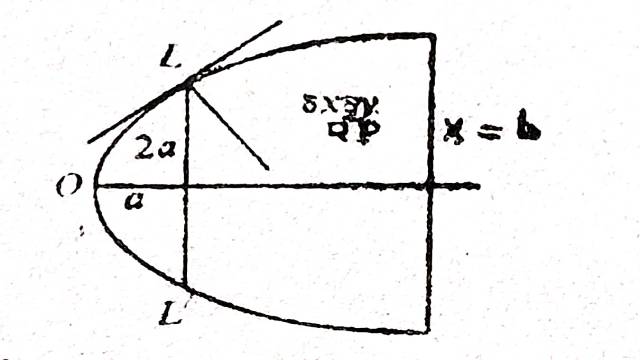
Example:11.शीर्ष से b दूरी पर एक द्विकोटि एवं 4a नाभिलम्ब के परवलयिक चाप द्वारा काटे एक समान पटल का नाभिलम्ब के एक सिरे पर स्पर्श रेखा एवं अभिलम्ब के सापेक्ष जड़त्व-गुणन ज्ञात करिए।
(Find P. I. of a uniform lamina bounded by a parabolic arc of latus rectum 4a and a double ordinate at a-distance b from the vertex about tangent and normal at the end of the latus rectum.)
Solution:नाभिलम्ब के सिरे के निर्देशांक (a,2a) तथा अवयव का द्रव्यमान

Product of Inertia in Dynamics

माना नाभिलम्ब तथा द्विकोटि के बीच के भाग का द्रव्यमान M है तब

M=\int_a^b 2 y \rho d x
परवलय का समीकरण y^2=4 a x \\ =\int_a^b 2 \sqrt{4ax} \rho d x \\ =4 a^{\frac{1}{2}} \rho \int_a^b x^{\frac{1}{2}} d x \\ =4 a^{\frac{1}{2}} \rho \left[x^{\frac{3}{2}}\right]_a^b \times \frac{2}{3} \\ M=\frac{8 }{3}a^{\frac{1}{2}} \rho \left(b^{\frac{3}{2}}-a^{\frac{3}{2}}\right) \\ \rho=\frac{3 M}{8 a^{\frac{1}{2}}\left(b^{\frac{3}{2}}-a^{\frac{3}{2}}\right)}
नाभिलम्ब के सिरे पर स्पर्श रेखा का समीकरण
\Rightarrow y y_1=2 a\left(x+x_1\right) \\ \therefore 2 y=2 a(x+a) \\ \Rightarrow y-x-a=0
तथा इस पर अभिलम्ब की समीकरण:
y-2 a=-1(x-a) \\ \Rightarrow y+x-3 a=0
अवयव P(x,y) से स्पर्शरेखा p_1 तथा p_2 अभिलम्ब पर लम्ब तथा हो तो:
p_1=\frac{y-x-a}{\sqrt{2}} तथा p_2=\frac{y+x-3 a}{\sqrt{2}}
अतः p_1 p_2=\frac{(y-x-a)}{\sqrt{2}} \times \frac{(y+x-3 a)}{\sqrt{2}} \\ =\frac{1}{2}\left[y^2-x^2-a(y+x+3 y-3 x)+3 a^2\right] \\ =\frac{1}{2}\left(y^2-x^2-4 a y+2 a x+3 a^2\right)
अतः स्पर्शरेखा तथा अभिलम्ब के सापेक्ष जड़त्व-गुणन

P.I.=\frac{1}{2} \int_a^b \int_{-\sqrt{(4 a x})}^{\sqrt{4 a x}}\left(y^2-x^2-4 a y+2 a x+3a^2\right) \rho dx dy \\ =\frac{\rho}{2} \int_a^b [\frac{1}{3} \cdot 2(4 a x)^{\frac{3}{2}}-0+ \left(3 a^2+2 a x-x^2\right)\cdot 2 \cdot \sqrt{4 a x}] dx \\ =\frac{\rho}{2} \int_a^b [\frac{2}{3} \times 8 a^{\frac{3}{2}} x^{\frac{3}{2}}+12 a^{\frac{5}{2}} x^{\frac{1}{2}}+8 a^{\frac{3}{2}} x^{\frac{3}{2}}-4 a^{\frac{1}{2}} x^{\frac{5}{2}}] d x \\ =2 \rho \int_a^b\left[\frac{4}{3} a^{\frac{3}{2}} x^{\frac{3}{2}}+3 a^{\frac{5}{2}} x^{\frac{1}{2}}+2 a^{\frac{3}{2}} x^{\frac{3}{2}}-a^{\frac{1}{2}} x^{\frac{5}{2}}\right] d x \\ =2 \rho a^{\frac{1}{2}} \int_a^b\left[\frac{4}{3} a x^{\frac{3}{2}}+3 a^2 x^{\frac{1}{2}}+2 a x^{\frac{3}{2}}-x^{\frac{5}{2}}\right] d x \\ =2 \rho a^{\frac{1}{2}}\left[\frac{4}{3} a \cdot \frac{x^{\frac{5}{2}}}{\frac{5}{2}}+\frac{3 a^2 x^{\frac{3}{2}}}{\frac{3}{2}}+\frac{2 a x^{\frac{5}{2}}}{\frac{5}{2}}-\frac{x^{\frac{7}{2}}}{\frac{7}{2}}\right]_a^b \\ =2 \rho a^{\frac{1}{2}}\left[\frac{8}{15} a^{x^{\frac{5}{2}}}+2 a^2 x^{\frac{3}{2}}+\frac{4}{5} a x^{\frac{5}{2}}-\frac{2}{7} x^{\frac{7}{2}}\right]_a^b \\ =2 \rho a^{\frac{1}{2}}[\frac{8}{15} a b^{\frac{5}{2}}+2 a^2 b^{\frac{3}{2}}+\frac{4}{5} a \cdot b^{\frac{5}{2}}-\frac{2}{7} b^{\frac{7}{2}} -\frac{8}{15} a \cdot a^{\frac{5}{2}}-2 a^2 a^{\frac{3}{2}}-\frac{4}{5} a \cdot a^{\frac{5}{2}}+\frac{2}{7} a^{\frac{7}{2}}] \\ =2 \rho a^{\frac{1}{2}}[\left( \frac{8}{15}+\frac{4}{5}\right) a b^{\frac{5}{2}}+2 a^2 b^{\frac{3}{2}}-\frac{2}{7} b^{\frac{7}{2}}-\left(\frac{8}{15} a^{\frac{7}{2}}+2 a^{\frac{7}{2}}+\frac{4}{5} a^{\frac{7}{2}}-\frac{2}{7} a^{\frac{7}{2}}\right)] \\ =2 a^{\frac{1}{2}} \rho [\frac{20}{15} a b^{\frac{5}{2}}+2 a^2 b^{\frac{3}{2}}-\frac{2}{7} b^{\frac{7}{2}}-\frac{(56+210+84-30) a^{\frac{7}{2}}}{105}] \\ =2 a^{\frac{1}{2}} \rho \cdot\left[\frac{4}{3} a b^{\frac{5}{2}}+2 a^2 b^{\frac{3}{2}}-\frac{2}{7} b^{\frac{7}{2}}-\frac{320}{105} a^{\frac{7}{2}}\right] \\ =2 a^{\frac{1}{2}} \times 2\left[\frac{2}{3} a b^{\frac{5}{2}}+a^2 b^{\frac{3}{2}}-\frac{1}{7} b^{\frac{7}{2}}-\frac{32}{21} a^{\frac{7}{2}}\right] \\ =4 a^{\frac{1}{2}} \rho \cdot\left[\frac{2}{3} a b^{\frac{5}{2}}+a^2 b^{\frac{3}{2}}-\frac{1}{7} b^{\frac{7}{2}}-\frac{32}{21} a^{\frac{7}{2}}\right] \\ =4 a^{\frac{1}{2}} \times \frac{3 M\left(\frac{2}{3} a b^{\frac{5}{2}}+a^2 b^{\frac{3}{2}}-\frac{1}{7} b^{\frac{1}{2}} -\frac{32}{21} a^{\frac{7}{2}}\right)}{8 a^{\frac{1}{2}}\left(b^{\frac{3}{2}}-a^{\frac{3}{2}}\right)} \\ =\frac{3 M}{2\left(b^{\frac{3}{2}}-a^{\frac{5}{2}}\right)}\left(\frac{2}{3} a b^{\frac{5}{2}}+a^2 b^{\frac{3}{2}}-\frac{1}{7} b^{\frac{7}{2}}-\frac{32}{21} a^{\frac{7}{2}}\right)
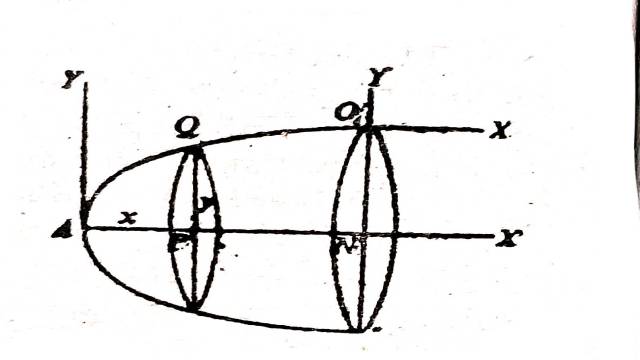
Example:12.एक ठोस परिक्रमण-परवलयज जिसकी अक्ष की लम्बाई जनक परवलय की नाभिलम्ब के बराबर है,के वृत्ताकार किनारे के एक बिन्दु पर परवलय की अक्ष के समान्तर तथा शीर्ष पर स्पर्शरेखा के समान्तर अक्षों के सापेक्ष जड़त्व-गुणन ज्ञात करो।
(Find P. I. of a solid parabola of revolution whose length of axis is equal to the latus rectum of the generating parabola about axes parallel to axis of the parabola and parallel to tangent at vertex at a point on a circular rim.)
Solution:माना जनक परवलय की समीकरण

y^2=4 a x जिसका नाभिलम्ब 4a जो अक्ष AN के बराबर है।वृत्तीय चक्रिका पर कोई बिन्दु O लो।
A से x दूरी पर चक्रिका है जिसकी त्रिज्या y है तथा द्रव्यमान=\pi \cdot y^2 \delta x \rho

Product of Inertia in Dynamics

यदि ठोस परवलयज का द्रव्यमान

M=\int_0^{4 a} \pi y^2 d x \rho \\ =\rho \int_0^{4 a} \pi \times 4 a x d x \\ =\pi \rho \times 4 a\left[\frac{x^2}{2}\right]_0^{4 a} \\ =2 \pi a \rho \times 16 a^2 \\ M=32 \pi a^3 \rho \\ \Rightarrow \rho=\frac{M}{32 \pi a^3} \\ \text{ON}^2=4 a \cdot \text{AN}=4 a \cdot 4 a \\ \Rightarrow \text{ON}^2=16 a^2 \\ \Rightarrow ON=4 a
PN=AN-AP=4a-x
समान्तर अक्षों के परितः जड़त्व आघूर्ण

P.I.=\int_0^{4 a} \pi y^2 \rho d x \cdot P N \cdot O N \\ =\pi \rho \int_0^{4 a} 4 a x \cdot 4 a(4 a-x) d x \\ =16 \pi a^2 \rho \int_0^{4 a}\left(4 a x-x^2\right) d x \\ =16 \pi a^2 \rho\left[2 a x^2-\frac{x^3}{3}\right]_0^{4 a} \\ =16 \pi a^2 \rho\left[32 a^3-\frac{64 a^3}{3}\right] \\ =16 \pi a^2 \rho \times \frac{32}{3} a^3 \\ \rho का मान रखने पर: 

=16 \pi a^2 \times \frac{32 a^3}{3} \times \frac{M}{32 \pi a^3} \\ =\frac{16 M a^2}{3} \\ \Rightarrow \text{P.I.}=\frac{16 m a^2}{3}
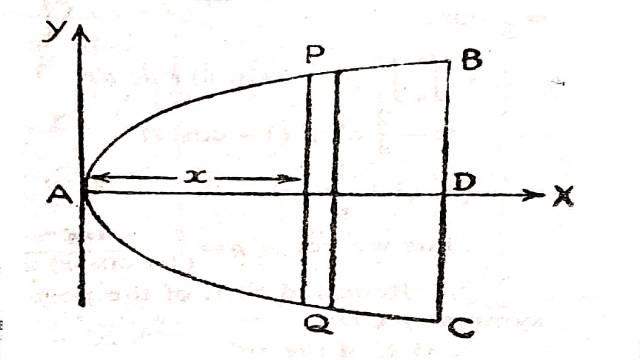
Example:13.प्रदर्शित करो कि शीर्ष से x-दूरी पर किसी काटे गए परवलय के क्षेत्रफल के भाग का शीर्ष पर स्पर्शरेखा के सापेक्ष जड़त्व आघूर्ण \frac{3}{7} m x^2 होगा तथा मुख्य व्यास के सापेक्ष \frac{1}{5} m y^2 होगा यहाँ y,x के संगत कोटि है।
(Show that M. I. of the part of the area of parabola cut off by any ordinate at a distance x from the vertex is \frac{3}{7} m x^2 about the tangent at the vertex and \frac{1}{5} m y^2 about the principal diameter where y is the ordinate corresponding to x.)
Solution:परवलय का समीकरण y^2=4 a x
परवलयिक क्षेत्र ABCA है जो शीर्ष से x दूरी पर काटा गया है जहाँ A शीर्ष है। \delta x चौड़ाई की पट्टी ली जो कि शीर्ष से X दूरी पर है।

Product of Inertia in Dynamics

पट्टी का द्रव्यमान=2 y \delta x \rho
सम्पूर्ण परवलय का द्रव्यमान=

m=\int_0^x 2 y \rho d x \\ =2 \rho \int_0^x \sqrt{4 a x} dx \\ =4 \rho a^{\frac{1}{2}} \left[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right]_0^x \\ =\frac{8 \rho a^{\frac{1}{2}} x^{\frac{3}{2}}}{3} \\ \Rightarrow \rho =\frac{3 m}{8 a^{\frac{1}{2}} x^{\frac{3}{2}}}
AY के सापेक्ष पट्टी का जड़त्व आघूर्ण =2 y \delta x \rho x^2 \\ =2 y \rho x^2 \delta x
A बिन्दु पर स्पर्शरेखा AY के सापेक्ष सम्पूर्ण क्षेत्र का जड़त्व आघूर्ण

M.I. =\int_0^x 2 y \rho x^2 d x \\ =\int_0^x 2 \rho \sqrt{4 a x} x^2 d x \\ =4 \rho a^{\frac{1}{2}} \int_0^x x^{\frac{5}{2}} d x \\ =4 \rho a^{\frac{1}{2}}\left[\frac{x^{\frac{7}{2}}}{\frac{7}{2}}\right]_0^x \\ =\frac{8}{7} \rho a^{\frac{1}{2}} x^{\frac{7}{2}} \\ \rho का मान रखने पर

\Rightarrow \text{M.I.}=\frac{8}{7} \times \frac{3 m a^{\frac{1}{2}}}{8 a^{\frac{1}{2}} x^{\frac{3}{2}}} \times x^{\frac{7}{2}} \\ \Rightarrow \text{M.I.}=\frac{3}{7} m x^2
पुनः पट्टी का AX के सापेक्ष जड़त्व आघूर्ण=2 y \delta x \rho\left(\frac{y^2}{3}\right)
अक्ष AX के सापेक्ष सम्पूर्ण क्षेत्र का जड़त्व आघूर्ण

=\frac{2}{3} \rho \int_0^{\frac{y^2}{4 a}} y^3 d x \\ =\frac{2}{3} \rho \int_0^{\frac{y^2}{4 a}}(4 a x)^{\frac{3}{2}} d x \\ =\frac{16}{3} \rho a^{\frac{3}{2}} \int_0^{\frac{y^2}{4 a}} x^{\frac{3}{2}} d x \\ =\frac{16}{3} \rho a^{\frac{3}{2}}\left[\frac{x^{\frac{5}{2}}}{\frac{5}{2}}\right]_0^{\frac{y^2}{4 a}} \\ =\frac{32}{15} \rho a^{\frac{3}{2}}\left[\frac{y^2}{4 a}\right]^{\frac{5}{2}} \\ =\frac{32}{15} \rho a^{\frac{3}{2}} \frac{y^5}{32 a^{\frac{5}{2}}}=\frac{1}{15} \rho \frac{y^5}{a} \\ m=\int_0^{\frac{y^2}{4 a}} 2 \rho y d x \\ =\rho \int_0^{\frac{y^2}{4 a}} 4 a^{\frac{1}{2}} \sqrt{x} d x \\ \Rightarrow m= \rho 4a^{\frac{1}{2}} \left[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right]_0^{\frac{y^2}{4 a}}=\frac{8 y^3 a^{\frac{1}{2}}}{3 \times 8 a^{\frac{3}{2}}} \rho \\ \Rightarrow \rho=\frac{3 m a}{y^3}\\ \rho का मान रखने पर
\Rightarrow \text{M.I.}=\frac{1}{15} \times \frac{3 m a}{y^3} \times \frac{y^5}{a} \\ \Rightarrow \text{M.I.}=\frac{1}{5} m y^2
उपर्युक्त उदाहरणों के द्वारा गतिविज्ञान में जड़त्व गुणन (Product of Inertia in Dynamics),जड़त्व-आघूर्ण (Moment of Inertia) को समझ सकते हैं।

3.गतिविज्ञान में जड़त्व गुणन की समस्याएँ (Product of Inertia in Dynamics Problems):

Product of Inertia in Dynamics

(1.)द्विपाशी r^2=a^2 \cos 2 \theta के अर्धलूप का इसकी अक्ष एवं इसके तल में,ध्रुव से होकर जानेवाली इसके अक्ष के लम्बवत अक्ष के सापेक्ष जड़त्व-गुणन ज्ञात करिए।
(Find the P. I. of a half loop of the lemniscate r^2=a^2 \cos 2 \theta about it axis and a line through the pole in its plane perpendicular to its axis)
(2.)लम्बवृत्तीय शंकु,जिसके आधार की त्रिज्या a है,का इसके अक्ष के परितः जड़त्व आघूर्ण ज्ञात करो।
(Find the M. I. of a right circular cone of base radius a about its axis)
उत्तर (Answers): (1.) \frac{M a^2}{12}
(2.) \frac{3 M}{10} a^2
उपर्युक्त सवालों को हल करने पर गतिविज्ञान में जड़त्व गुणन (Product of Inertia in Dynamics),जड़त्व-आघूर्ण (Moment of Inertia) को ठीक से समझ सकते हैं।

Also Read This Article:- Moment of Inertia in Dynamics

4.गतिविज्ञान में जड़त्व गुणन (Frequently Asked Questions Related to Product of Inertia in Dynamics),जड़त्व-आघूर्ण (Moment of Inertia) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:

गतिविज्ञान में जड़त्व गुणन (Product of Inertia in Dynamics) के इस आर्टिकल में किसी
पिण्ड का किसी रेखा अथवा दो लम्ब निर्देशाक्ष के सापेक्ष जड़त्व गुणनफल ज्ञात करना सीखेंगे।