Probability Class 10
1.प्रायिकता कक्षा 10 (Probability Class 10):
प्रायिकता कक्षा 10 (Probability Class 10) परिभाषा:जब किसी घटना के घटित होने की संभावना संख्यात्मक रूप में व्यक्त की जाती है तो उसे प्रायिकता कहते हैं।
प्रायोगिक या आनुभविक प्रायिकता (Experimental or Empirical Probability):जिस प्रायिकता का मापन वास्तविक प्रयोगों के परिणामों तथा घटनाओं के घटित होने की पर्याप्त रिकॉर्डिंग (Recording) के आधार पर करते हैं,उस प्रायिकता को प्रायोगिक या आनुभविक प्रायिकता कहते हैं।
उदाहरणार्थ:जब हम एक सिक्का उछालें तो यह समतल पर गिरेगा।यह एक क्रिया या प्रयोग है जिससे दो परिणाम प्राप्त हो सकते हैं:
चित्त (अशोक वाला) तल दिखाई दे अथवा पट (दूसरा तल) दिखाई दे,ये दो संभव घटनाएं (Events) हैं।
(i)इस प्रकार हम देखते हैं कि सिक्का उछालने के किसी प्रयोग में कुल संभावित घटनाएं दो हैं।चित्त गिरने की संभावना दो घटनाओं में से एक है और पट गिरने की संभावना भी उतनी ही है।तब हम गणित की भाषा में कहते हैं कि सिक्के के चित्त गिरने की प्रायिकता \frac{1}{2} है।सिक्के के पट गिरने की प्रायिकता \frac{1}{2} है।
(ii)किसी चुनाव में A,B,C,D चार उम्मीदवार खड़े हैं तब सफल प्रत्याशी के चुनाव की कुल चार संभावनाएं हैं क्योंकि चारों प्रत्याशियों में कोई भी सफल हो सकता है तब प्रत्याशी A की सफलता की संभावना चार में से एक है।हम गणित की भाषा में कह सकते हैं कि प्रत्याशी A की सफलता की प्रायिकता \frac{1}{4} है;शेष प्रत्याशियों B,C व D की सफलता की भी प्रायिकता उतनी ही है।यहाँ हम कह सकते हैं कि किसी प्रत्याशी की असफलता की प्रायिकता \frac{3}{4} है क्योंकि एक प्रत्याशी के सफल होने की दशा में शेष तीन के असफल होने की घटना अवश्य घटित होगी।
(iii)ताश की गड्डी में से एक पत्ता खींचिए। इसके लाल होने की प्रायिकता पर विचार कीजिए।कुल 52 पत्तों की गड्डी में 26 लाल और 26 काले पत्ते होंगे तब पत्ते के लाल होने की प्रायिकता \frac{26}{52} या \frac{1}{2} है।खींचे गए पत्ते के लाल न होने की भी प्रायिकता \frac{26}{52} या \frac{1}{2} ही है।
यादृच्छया उछाल (Random toss): किसी सिक्के को बिना किसी पक्षपात (bias) या रुकावट के स्वतंत्रता पूर्वक गिरने दिया जाता है तो उसे यादृच्छया उछाल कहते हैं।
समप्रायिक (Equally likely): जब किसी यादृच्छया प्रयोग में किसी घटना E के सभी परिणामों के प्राप्त होने की संभावना समान होती है तो यह परिणाम समप्रायिक कहलाते हैं।
जैसे:जब किसी सिक्के को उछालने में चित्त या पट अथवा पासे की उछाल में पासे पर अंकित अंकों में से कोई अंक प्राप्त होने की घटना समप्रायिक घटनाएं हैं।
सैद्धान्तिक प्रायिकता (Theoretical Probability):किसी प्रयोग में यदि एक घटना \bar{E} घटित होती है और यह कल्पना करने पर प्रयोग में घटना E के सभी प्रणाम P(E)=\frac{\text{ घटना E के अनुकूल परिणामों की संख्या }}{\text{ प्रयोग के सभी परिणामों की संख्या }}
इस प्रकार से अवकलित प्रायिकता को सैद्धांतिक प्रायिकता कहते हैं।
प्रारंभिक घटना (Elementary Event):वह घटना है जिसका केवल एक ही परिणाम है।किसी पासे को उछालने पर 5 प्राप्त होना प्रारंभिक घटना है क्योंकि 5 प्राप्त होने का केवल एक ही परिणाम है।परंतु विषम या सम संख्या प्राप्त होना प्रारंभिक घटना नहीं है क्योंकि विषम संख्या प्राप्त होने की घटना के 1,3,5 तीन परिणाम हैं।ऐसे ही सम संख्या या 5 से छोटी संख्या प्राप्त करने की घटना भी प्रारंभिक घटना नहीं है क्योंकि इनके परिणाम एक से अधिक है।
किसी प्रयोग की सभी प्रारंभिक घटनाओं का योग 1 होता है।
असंभव घटना (Impossible Event):जिस घटना की प्रायिकता शून्य होती है अर्थात् उस घटना का घटित होना असंभव हो तो उस घटना को असंभव घटना (Impossible Event) कहते हैं। किसी पासे की उछाल में “6 से बड़ा अंक प्राप्त होने की घटना” असंभव घटना है।
निश्चित घटना (Sure Event):किसी घटना की प्रायिकता 1 हो तो उस घटना को निश्चित घटना (Sure Event) कहते हैं।
जैसे:किसी पासे की फेंक में 7 से छोटी संख्या प्राप्त होने की घटना के सभी परिणाम 1,2,3,4,5,6 संभव है।यह एक निश्चित घटना है।
घटना (E) घटित नहीं हो:इसे E से व्यक्त करते हैं तथा घटना को “E नहीं से” जाना जाता है।
यदि किसी घटना की प्रायिकता सदैव शून्य के बराबर या उससे अधिक तथा एक के बराबर या उससे कम होती है। 0 \leq P(E) \leq 1
ताश के पत्ते (Playing Cards):
ताश की गड्डी में कुल पत्तों की संख्या=52
कुल पत्ते 4 समूहों में विभाजित होते हैं:
(1.)हुकुम (Spades) (2.)पान (Hearts) (3.)ईंट (Diamonds) (4.)चिड़ी (Clubs)
प्रत्येक समूह में 13 पत्ते होते हैं अर्थात्
हुकुम के 13,पान के 13,ईंट के 13 और चिड़ी के 13 पत्ते होते हैं।
काले रंग के पत्ते:हुकुम 13 और चिड़ी 13=कुल 26
लाल रंग के पत्ते:पान 13 व ईंट 13=कुल 26
प्रत्येक समूह में इक्का (ace),बादशाह (King),बेगम (queen) और गुलाम (jack) उच्चक्रम के पत्ते होते हैं।इक्का (ace) पहले क्रम का पत्ता और बादशाह (King),बेगम (queen) तथा गुलाम (jack)फेस पत्ते (Face Cards) कहलाते हैं।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Zeroes of Quadratic Polynomial
2.प्रायिकता कक्षा 10 के उदाहरण (Probability Class 10 Examples):
Example:1.एक थैले में 3 लाल और 5 काली गेंदे हैं।इस थैले में से एक गेंद यादृच्छया निकाली जाती है।इसकी प्रायिकता क्या है कि गेंद
(i)लाल हो? (ii)लाल नहीं हो?
Solution:थैले में गेंदों की कुल संख्या=3 लाल+5 काली=8
थैले में से एक गेंद यादृच्छया निकालने पर कुल सम्भावित परिणाम=8
(i)गेंद लाल (R) होने की घटना के अनुकूल परिणाम=3
गेंद लाल होने की प्रायिकता
P(R)=\frac{\text{ घटना (R) के अनुकूल परिणाम }}{\text{ कुल सम्भव परिणाम }} \\ =\frac{3}{8}
अतः गेंद लाल होने की प्रायिकता=\frac{3}{8}
(ii)गेंद लाल न होने की प्रायिकता
=1-गेंद लाल होने की प्रायिकता =1-\frac{3}{8}=\frac{5}{8}
अतः गेंद लाल न हो इसकी प्रायिकता=\frac{5}{8}
Example:2.एक डिब्बे में 5 लाल कंचे,8 सफेद कंचे और 4 हरे कंचे हैं।इस डिब्बे में से एक कंचा यादृच्छया निकाला जाता है।इसकी क्या प्रायिकता है कि निकाला गया कंचा
(i)लाल है? (ii)सफेद है? (iii)हरा नहीं है?
Solution:लाल कंचों की संख्या=5
सफेद कंचों की संख्या=8
हरे कंचों की संख्या=4
डिब्बे में कंचों की कुल संख्या=5+8+4=17
जब डिब्बे में से एक कंचा निकाला जाता है तो सम्भावित कुल परिणाम=17
(i)निकाला गया कंचा लाल (R) होने की घटना के अनुकूल परिणाम=5
अतः निकाले गए कंचें के लाल होने की प्रायिकता
P(R)=\frac{\text{ घटना (R) के अनुकूल परिणामों की संख्या}}{\text{ कुल सम्भव परिणाम }} \\ \Rightarrow P(R)=\frac{5}{17}
(ii)निकाला गया कंचा सफेद (W) होने के अनुकूल परिणाम=8
अतः निकाले गए कंचें के सफेद होने की प्रायिकता
P(W)=\frac{\text{ घटना (E) के अनुकूल परिणामों की संख्या}}{\text{ कुल सम्भव परिणाम }} \\ \Rightarrow P(R)=\frac{8}{17}
(iii)गेंद के हरी (G) होने के अनुकूल परिणाम=4
गेंद के हरी (G’) न होने के अनुकूल परिणाम=17-4=13
अतः निकाली गई गेंद हरी न होने की प्रायिकता
P(G’)=\frac{ \text{ घटना G' के अनुकूल परिणामों की संख्या}}{ \text{कुल सम्भव परिणाम }} \\ =\frac{13}{17}
Example:3.एक पिग्गी बैंक (Piggy Bank) में 50 पैसे के सौ सिक्के,1 रु. के पचास सिक्के,2 रु. के बीस सिक्के और 5 रु. के दस सिक्के हैं।यदि पिग्गी बैंक को हिलाकर उल्टा करने पर कोई एक सिक्के गिरने का परिणाम समप्रायिक है तो इसकी क्या प्रायिकता है कि वह गिरा हुआ सिक्का
(i)50 पैसे का होगा? (ii)5 रु. का नहीं होगा?
Solution:50 पैसे के सिक्कों की संख्या=100
1 रु. के सिक्कों की संख्या=50
2 रु. के सिक्कों की संख्या=20
5 रु. के सिक्कों की संख्या=10
सिक्कों की कुल संख्या=100+50+20+10=180
(i)50 पैसे के 100 सिक्के हैं।
50 पैसे के सिक्के प्राप्त करने की प्रायिकता
=\frac{ \text{ अनुकूल परिणामों की संख्या }}{\text{ परिणामों की कुल संख्या }}=\frac{100}{180}
P(50 पैसे के सिक्के)=\frac{5}{9}
(ii)5 रु. के सिक्कों की संख्या=10
5 रु. के सिक्के प्राप्त करने की प्रायिकता=\frac{\text{ अनुकूल परिणामों की संख्या}}{\text{ परिणामों की कुल संख्या }}
P(5 रु. के सिक्के)=\frac{10}{180}=\frac{1}{18}
5 रु. के सिक्के प्राप्त न करने की प्रायिकता
=1-P(5 रु. के सिक्के)=1-\frac{1}{18}=\frac{18-1}{18}=\frac{17}{18}
Example:4.गोपी अपने जलकुण्ड (aquarium) के लिए एक दुकान से मछली खरीदती है।दुकानदार एक टंकी जिसमें 5 नर मछली और 8 मादा मछली हैं, में से एक मछली यादृच्छया उसे देने के लिए निकालती है।इसकी क्या प्रायिकता है कि निकाली गई मछली नर मछली है।
Solution:नर मछलियों की संख्या=5
मादा मछलियों की संख्या=8
जल-जीव कुण्ड में मछलियों की कुल संख्या=5+8=13
नर मछली प्राप्त करने की प्रायिकता=\frac{ \text{ अनुकूल परिणामों की संख्या}}{ \text{ परिणामों की कुल संख्या }}
P(नर मछली)=\frac{5}{13}
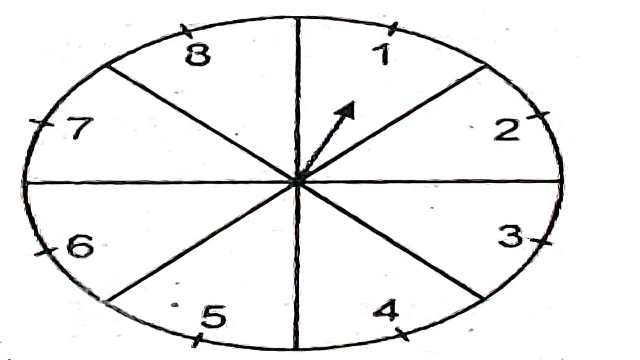
Example:5.संयोग (Chance) के एक खेल में, एक तीर को घुमाया जाता है, जो विश्राम में आने के बाद संख्याओं 1,2,3,4,5,6,7 और 8 में से किसी एक संख्या को इंगित करता है।(आकृति देखिए) यदि ये सभी परिणाम समप्रायिक हों तो इसकी क्या प्रायिकता है कि यह तीर इंगित:
(i)8 को करेगा?
(ii)एक विषम संख्या को करेगा?
(iii)2 से बड़ी संख्या को करेगा?
(iv)9 से छोटी संख्या को करेगा?
Solution:संयोग के खेल में जब तीर को घुमाया जाता है तो तीर के विश्राम में आने पर कुल परिणाम=(1,3,3,4,5,6,7,8)=8
(i)तीर द्वारा संख्या 8 को इंगित करने के कुल अनुकूल परिणाम=1
उक्त घटना की प्रायिकता
P=\frac{\text{ घटना के अनुकूल परिणाम}}{\text{ कुल सम्भव परिणाम}} \\ =\frac{1}{8}
अतः संख्या 8 को इंगित करने के परिणाम=\frac{1}{8}
(ii)तीर द्वारा एक विषम संख्या अंकित करनेवाले के परिणाम=(1,3,5,7)=4
विषम संख्या इंगित होने की प्रायिकता=\frac{ \text{ घटना के अनुकूल परिणाम }}{\text{ कुल सम्भव परिणाम }} \\=\frac{4}{8}=\frac{1}{2}
अतः विषम संख्या को इंगित करने की प्रायिकता=\frac{1}{2}
(iii)2 से बड़ी संख्या को इंगित करने की घटना के कुल अनुकूल परिणाम=(3,4,5,6,7,8)=6
2 से बड़ी संख्या को इंगित करने की प्रायिकता=घटना के अनुकूल परिणाम=\frac{\text{ घटना के अनुकूल परिणाम}}{\text{ कुल सम्भव परिणाम }} =\frac{6}{8}=\frac{3}{4}
अतः 2 से बड़ी संख्या इंगित करने की प्रायिकता=\frac{3}{4}
(iv)9 से छोटी संख्या इंगित करने की प्रायिकता=\frac{ \text{ घटना के अनुकूल परिणाम}}{\text{ कुल सम्भव परिणाम }} \\=\frac{8}{8}=1
Example:6.एक पासे को एक बार फेंका जाता है।निम्नलिखित को प्राप्त करने की प्रायिकता ज्ञात कीजिए:
(i)एक अभाज्य संख्या
(ii)2 तथा 3 के बीच स्थित कोई संख्या
(iii)एक विषम संख्या
Solution:(i)एक पासे को यादृच्छया फेंके जाने पर प्राप्त होने वाले सभी सम्भव परिणामों की संख्या=(2,3,5)=3
अभाज्य संख्या प्राप्त करने की प्रायिकता=\frac{3}{6}=\frac{1}{2}
(ii)2 और 6 के बीच स्थित संख्याएँ=(3,4,5)=3
2 और 6 के बीच स्थित संख्या प्राप्त करने की प्रायिकता=\frac{3}{6}=\frac{1}{2}
(iii)विषम संख्याएँ=(1,3,5)=3
एक विषम संख्या प्राप्त करने की प्रायिकता=\frac{3}{6}=\frac{1}{2}
Example:7.52 पत्तों को अच्छी प्रकार से फेंटी गई एक गड्डी में से एक पत्ता निकाला जाता है।निम्नलिखित को प्राप्त करने की प्रायिकता ज्ञात कीजिए:
(i)लाल रंग का बादशाह,
(ii)एक फेस कार्ड अर्थात् तस्वीर वाला पत्ता,
(iii)लाल रंग का तस्वीर वाला पत्ता
(iv)पान का गुलाम
(v)हुकुम का पत्ता
(vi)एट ईंट की बेगम
Solution:ताश की गड्डी में 52 पत्ते होते हैं।गड्डी को अच्छी तरह फेंटकर गड्डी में से एक पत्ता निकालने पर पत्ता क्या है, इसके कुल सम्भावित परिणामों की संख्या=52
(i)लाल रंग का बादशाह होने की घटना (R):
गड्डी में कुल 4 बादशाह होते है जिनमें पान तथा ईंट का बादशाह लाल होता है।
लाल रंग का बादशाह प्राप्त होने के अनुकूल परिणाम=2
घटना R की प्रायिकता
P(R)=\frac{ \text{ घटना R के अनुकूल परिणाम }}{\text{ कुल सम्भव परिणाम }} \\=\frac{2}{52}=\frac{1}{26}
अतः लाल बादशाह होने की प्रायिकता=\frac{1}{26}
(ii)एक फेस कार्ड अर्थात् तस्वीर वाला पत्ता होने की घटना (E);
प्रत्येक समूह में 3 फेस कार्ड्स (बादशाह, बेगम व गुलाम) होते हैं।
गड्डी में कुल फेस कार्ड=3 × 4=12
घटना (E) के अनुकूल परिणाम=12
घटना (E) की प्रायिकता=\frac{ \text{ घटना के अनुकूल परिणाम}}{\text{ कुल सम्भव परिणाम }}\\ =\frac{12}{52}=\frac{3}{13}
अतः एक फेस कार्ड्स अर्थात् तस्वीर वाला पत्ता होने की प्रायिकता=\frac{3}{13}
(iii)लाल रंग का तस्वीर वाला पत्ता (A):
कुर फेस कार्ड्स=12
लाल रंग के तस्वीर वाले पत्तों की संख्या=6
तब,घटना (A) के अनुकूल परिणाम=6
घटना (A) की प्रायिकता
P(A)=\frac{\text{घटना A के अनुकूल परिणाम}}{\text{कुल सम्भव परिणाम}} \\=\frac{6}{52}=\frac{3}{26}
अतः लाल रंग का तस्वीर वाला पत्ता निकलने की प्रायिकता=\frac{3}{26}
(iv)पान का गुलाम होने की घटना (B):
गड्डी में पान का एक ही गुलाम होता है।अतः घटना B के अनुकूल परिणामों की संख्या=1
घटना (B) की प्रायिकता=\frac{\text{ घटना B के अनुकूल परिणाम }}{\text{कुल सम्भव परिणाम }} \\=\frac{1}{52}
अतः निकाले गए पत्ते के पान का गुलाम होने की प्रायिकता=\frac{1}{52}
(v)हुकुम का पत्ता होने की घटना (C):
गड्डी में हुकुम के पत्तो की संख्या=13
घटना C के अनूकुल परिणामों की संख्या=13
घटना (C) की प्रायिकता P(C)=\frac{13}{52}=\frac{1}{4}
अतः निकाला गया हुकुम का पत्ता होने की प्रायिकता=\frac{1}{4}
(vi)ईंट की बेगम होने की घटना (D):
गड्डी में ईंट की केवल एक ही बेगम होती है।
घटना D के अनुकूल परिणामों की संख्या=1
घटना (D) की प्रायिकता
P(D)=\frac{\text{ घटना (D) के घटित होने के अनुकूल परिणाम}}{\text{कुल सम्भव परिणाम}}\\=\frac{1}{52}
अतः निकाला गया पत्ता ईंट की बेगम होने की प्रायिकता=\frac{1}{52}
उपर्युक्त उदाहरणों द्वारा प्रायिकता कक्षा 10 (Probability Class 10) को समझ सकते हैं।
3.प्रायिकता कक्षा 10 की समस्याएं (Probability Class 10 Problems):
(1.)साधारण पासों के एक युग्म को फेंकने पर कुल योग 8 आने की प्रायिकता ज्ञात कीजिए।
(2.) यदि दो अपक्षपातपूर्ण सिक्के एक साथ उछाले जाते हैं तो निम्न घटनाओं की प्रायिकता होगी:
(i)दोनों चित्त प्राप्त हों,
(ii)एक पट पर प्राप्त हों,
(iii)कम से कम एक चित्त प्राप्त हो,
(iv)अधिक से अधिक एक चित्त प्राप्त हो।
(3.)रमेश और महेश दो मित्र हैं।इसकी प्रायिकता क्या होगी कि दोनों
(i)के जन्मदिन एक ही हों?
(ii)जन्मदिन भिन्न;भिन्न हों? (लीप वर्ष को छोड़ते हुए)
(4.)एक थैली में 5 लाल,8 सफेद,4 हरी तथा 7 काली गेंदे हैं।यदि यादृच्छया एक गेंद निकाली जाती है तो प्रायिकता ज्ञात कीजिए कि वह गेंद
(i)काली है
(ii)लाल है
(iii)हरी नहीं है।
उत्तर (Answers):(1.)\frac{5}{36}
(2.)(i) \frac{1}{4} \quad (ii)\frac{1}{2} \quad (iii) \frac{3}{4} \quad (iv)\frac{3}{4}
(3.)(i) \frac{1}{365} \quad (ii) \frac{364}{365}
(4.)(i)\frac{7}{24} \quad (ii)\frac{5}{24} \quad (iii) \frac{5}{6}
उपर्युक्त सवालों को हर करने पर प्रायिकता कक्षा 10 (Probability Class 10) को ठीक से समझ सकते हैं।
Also Read This Article:-Surface Area and Volume of a Sphere
4.प्रायिकता कक्षा 10 (Probability Class 10 probability) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.यदि कोई घटना घटित नहीं हो सकती तो उसकी प्रायिकता लिखिए। (If an event cannot happen, write down its probability):
उत्तर:घटना घटित न होने की प्रायिकता जीरो (0) होती है।
प्रश्न:2.निश्चित घटना की प्रायिकता लिखिए। (Write down the probability of a certain event):
उत्तर:निश्चित घटना की प्रायिकता एक होती है।
प्रश्न:3.प्रायिकता की सीमा बताइए। (What is the extent of probability?):
उत्तर:प्रायिकता की सीमा 0 \leq P(A) \leq 1 है।
प्रश्न:4.यदि घटना घटने की प्रायिकता P(A) है तो घटना न घटने की प्रायिकता लिखिए। (If the probability of occurrence is P(A) then write down the probability that the event does not occur):
उत्तर:घटना न घटने की प्रायिकता=1-P(A)
प्रश्न:5.किसी प्रयोग की सभी प्रारंभिक घटनाओं की प्रायिकताओं का योग लिखिए। (Write the sum of probabilities of all the elementary events of an experiment):
उत्तर:किसी प्रयोग की सभी प्रारंभिक घटनाओं की प्रायिकताओं का योग ‘1’ होता है।
प्रश्न:6.यदि P(E)=0.05 है तो ‘E नहीं’ की प्रायिकता बताइए। (If P(E)=0.05 then give the probability of ‘not E’):
उत्तर:यदि P(E)=0.05
‘E नहीं’ की प्रायिकता
P(\bar{E})=1-P(E)
=1-0.05=0.95
उपर्युक्त प्रश्नों के उत्तर द्वारा प्रायिकता कक्षा 10 (Probability Class 10) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
- 1.प्रायिकता कक्षा 10 (Probability Class 10):
- 2.प्रायिकता कक्षा 10 के उदाहरण (Probability Class 10 Examples):
- 3.प्रायिकता कक्षा 10 की समस्याएं (Probability Class 10 Problems):
- 4.प्रायिकता कक्षा 10 (Probability Class 10 probability) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:
- प्रश्न:1.यदि कोई घटना घटित नहीं हो सकती तो उसकी प्रायिकता लिखिए। (If an event cannot happen, write down its probability):
- प्रश्न:2.निश्चित घटना की प्रायिकता लिखिए। (Write down the probability of a certain event):
- प्रश्न:3.प्रायिकता की सीमा बताइए। (What is the extent of probability?):
- प्रश्न:4.यदि घटना घटने की प्रायिकता P(A) है तो घटना न घटने की प्रायिकता लिखिए। (If the probability of occurrence is P(A) then write down the probability that the event does not occur):
- प्रश्न:5.किसी प्रयोग की सभी प्रारंभिक घटनाओं की प्रायिकताओं का योग लिखिए। (Write the sum of probabilities of all the elementary events of an experiment):
- प्रश्न:6.यदि P(E)=0.05 है तो ‘E नहीं’ की प्रायिकता बताइए। (If P(E)=0.05 then give the probability of ‘not E’):
- प्रायिकता कक्षा 10 (Probability Class 10)
Probability Class 10
प्रायिकता कक्षा 10
(Probability Class 10)
Probability Class 10
प्रायिकता कक्षा 10 (Probability Class 10) परिभाषा:जब किसी घटना के घटित होने की संभावना
संख्यात्मक रूप में व्यक्त की जाती है तो उसे प्रायिकता कहते हैं।