Point of Inflexion in Calculus
1.कलन में नति परिवर्तन बिन्दु (Point of Inflexion in Calculus),अवकलन गणित में नति परिवर्तन बिन्दु (Point of Inflexion in Differential Calculus):
कलन में नति परिवर्तन बिन्दु (Point of Inflexion in Calculus) को जानने के लिए वक्रों की अवतलता (Concavity),उत्तलता (Convexity),नति परिवर्तन बिन्दु को जानना आवश्यक है।पहले नति परिवर्तन बिन्दु पर उदाहरणों को समझेंगे।इसके पश्चात उपर्युक्त तीनों की परिभाषा देंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Asymptotes of Polar Curves
2.कलन में नति परिवर्तन बिन्दु के साधित उदाहरण (Point of Inflexion in Calculus Solved Examples):
निम्नलिखित वक्रों के नति-परिवर्तन बिन्दु ज्ञात कीजिएः
(Find the point of inflexion for the following curves):
Example:1. y=x^4-6 x^3+12 x^2+5 x+7
Solution: y=x^4-6 x^3+12 x^2+5 x+7 \ldots(1)
समीकरण (1) के दोनों पक्षों का x के सापेक्ष अवकलन करने परः
\frac{d y}{d x}=4 x^3-18 x^2+24 x+5
पुनः x के सापेक्ष अवकलन करने परः
\frac{d^2 y}{d x^2}=12 x^2-36 x+24
पुनः x के सापेक्ष अवकलन करने परः
\frac{d^3 y}{d x^3}=24 x-36
नति परिवर्तन बिन्दु के लिएः
\frac{d^2 y}{d x^2}=0 तथा \frac{d^2 y}{d x^3} \neq 0
अब \frac{d^2 y}{d x^2}=0 सेः
\Rightarrow 12 x^2-36 x+24=0 \\ \Rightarrow 12\left(x^2-3 x+2\right)=0 \\ \Rightarrow x^2-2 x-x+2=0 \\ \Rightarrow x(x-2)-1(x-2)=0 \\ \Rightarrow(x-1)(x-2)=0 \\ \Rightarrow x=1,2
अब (1) से इनके संगत y के मान होंगेः
y=(1)^4-6(1)^3+12(1)^2+5 \times 1+7 \\ =1-6+12+5+7 \\ y =19 \\ y =(2)^4-6(2)^3+12(2)^2+5 \times 2+7 \\ =16-48+48+10+7 \\ y =33 \\ (1,19) ;(2,33) \\ \left(\frac{d^3 y}{d x^3}\right)_{(1,19)}=24 \times 1-36=-12 \neq 0 \\ \left(\frac{d^3 y}{d x^3}\right)_{(2,33)}=24 \times 2-36=12 \neq 0
अतः (1,19),(2,33) नति परिवर्तन बिन्दु हैं।
Example:2. y^2=x(x+1)^2
Solution: y^2=x(x+1)^2
दिए हुए समीकरण को निम्न प्रकार से लिखा जा सकता हैः
y=(x+1) \sqrt{x} \\ \Rightarrow y=x^{\frac{3}{2}}+x^{\frac{1}{2}} \ldots(1)
समीकरण (1) के दोनों पक्षों का x के सापेक्ष अवकलन करने परः
\frac{d y}{d x}=\frac{3}{2} x^{\frac{1}{2}}+\frac{1}{2} x^{-\frac{1}{2}}
पुनः x के सापेक्ष अवकलन करने परः
\frac{d^{2}y}{d x^2}=\frac{3}{4} x^{-\frac{1}{2}}-\frac{1}{4} x^{-\frac{3}{2}}
पुनः x के सापेक्ष अवकलन करने परः
\frac{d^3 y}{d x^3}=-\frac{3}{8} x^{-\frac{3}{2}}+\frac{3}{8} x^{-\frac{5}{2}}
नति परिवर्तन बिन्दु के लिएः
\frac{d^2 y}{d x^2}=0 तथा \frac{d^3 y}{d x^3} \neq 0
अब \frac{d^2 y}{d x^2}=0 सेः
\frac{3}{4} x^{-\frac{1}{2}}-\frac{1}{4} x^{-\frac{3}{2}}=0 \\ \Rightarrow \frac{3}{x^{\frac{1}{2}}}=x^{-\frac{3}{2}} \\ \Rightarrow \frac{3}{x^{\frac{1}{2}}}=\frac{1}{x^{\frac{3}{2}}} \\ \Rightarrow 3 x-1=0 \\ \Rightarrow x=\frac{1}{3}
अब (1) से इनके संगत y के मान होंगेः
y=\pm\left(\frac{1}{3}+1\right) \sqrt{\left(\frac{1}{3}\right)} \\ y= \pm \frac{4}{3 \sqrt{3}} \\ \left(\frac{1}{3}, \pm \frac{4}{3 \sqrt{3}}\right) \\ \left(\frac{d^3 y}{d x^3}\right)_{\left(\frac{1}{3}, \pm \frac{4}{3 \sqrt{3}} \right)}=-\frac{3}{8} \cdot \frac{1}{\left(\frac{1}{3}\right)^{\frac{3}{2}}}+\frac{3}{8} \cdot \frac{1}{\left(\frac{1}{3}\right)^{\frac{5}{2}}} \\ =-\frac{3}{8} \times 3 \sqrt{3}+\frac{3}{8} \times 9 \sqrt{3} \\ =\frac{-9 \sqrt{3}+27 \sqrt{3}}{8} \\=\frac{18 \sqrt{3}}{8} \\ \left(\frac{d^3 y}{d x^3}\right)_{\left(\frac{1}{3}, \pm \frac{4}{3 \sqrt{3}} \right)}=\frac{9 \sqrt{3}}{4} \neq 0 \\ \left(\frac{d^3 y}{d x^3}\right)_{\left(\frac{1}{3}, \pm \frac{4}{3 \sqrt{3}}\right)} \neq 0
अतः ये बिन्दु नति परिवर्तन बिन्दु हैं।
Example:3. y=\frac{1-x}{1+x^2}
Solution: y=\frac{1-x}{1+x^2} \ldots(1)
समीकरण (1) के दोनों पक्षों का x के सापेक्ष अवकलन करने परः
\frac{d y}{d x}=\frac{\left(1+x^2\right)(-1)-(1-x) 2 x}{\left(1+x^2\right)^2} \\ =\frac{-1-x^2-2x+ 2x^2}{\left(1+x^2\right)^2} \\ \frac{d y}{d x} =\frac{x^2-2 x-1}{\left(1+x^2\right)^2}
पुनः x के सापेक्ष अवकलन करने परः
\frac{d^2 y}{d x^2}=\frac{\left(1+x^2\right)^2(2 x-2)-\left(x^2-2 x-1\right) \cdot 2\left(1+ x^2 \right) \cdot 2 x}{\left(1+x^2\right)^4} \\ =\frac{\left(1+x^2\right)\left[\left(1+x^2\right)(2 x-2)-4 x\left(x^2-2x-1\right) \right]}{\left(1+x^2\right)^4} \\ =\frac{2 x-2+2 x^3-2 x^2-4 x^3+8 x^2+4 x}{\left(1+x^2\right)^3} \\ \Rightarrow \frac{d^2 y}{dx^{2}}=\frac{-2 x^3+6 x^2+6 x-2}{\left(1+ x^2\right)^3}
पुनः x के सापेक्ष अवकलन करने परः
\frac{d^3 y}{d x^3} =\frac{\left(1+x^2\right)^3\left(-6 x^2+12 x+6\right)-\left(-2 x^3+6 x^2+6 x-2\right) \cdot 3\left(1+x^2\right)^2 \cdot 2 x}{\left(1+x^2\right)^6} \\ =\left(1+x^2\right)^2 \left[\frac{\left( 1+x^2\right)\left(-6 x^2+12 x+6\right)-6 x\left(-2 x^3+6 x^2+6 x-2\right)}{\left(1+x^2 \right)^6}\right] \\ =\frac{-6 x^2+12 x+6-6 x^4+12 x^3+6 x^2+12 x^4-36 x^3-36 x^2+12 x}{\left(1+x^2\right)^4} \\ =\frac{6 x^4-24 x^3-36 x^2+24 x+6}{\left(1+x^2\right)^4} \\ \Rightarrow \frac{d^3 y}{d x^3}=\frac{6 x^4-24 x^3-36 x^2+24 x+6}{\left(1+x^2\right)^4}
नति परिवर्तन बिन्दु के लिएः
\frac{d^2 y}{d x^{2}}=0 तथा \frac{d^3 y}{d x^3} \neq 0
अब \frac{d^2 y}{d x^2}=0 सेः
\frac{-2 x^3+6 x^2+6 x-2}{\left(1+x^2\right)^3}=0 \\ \Rightarrow-2 x^3-2 x^2+8 x^2+8 x-2 x-2=0 \\ \Rightarrow-2 x^2(x+1)+8 x(x+1)-2(x+1)=0 \\ \Rightarrow(x+1)\left(-2 x^2+8 x-2\right)=0 \\ \Rightarrow x+1=0 \Rightarrow x=-1 \\ \Rightarrow -2 x^2+8 x-2=0 \\ x=\frac{-8 \pm \sqrt{(8)^2-4 \times -2 \times -2}}{2 \times -2} \\ =\frac{-8 \pm \sqrt{64-16}}{-4} \\ =\frac{-8 \pm \sqrt{48}}{-4} \\ =\frac{-8 \pm 4 \sqrt{3}}{-4} \\ x=2 \pm \sqrt{3} \\ x=-1,2 \pm \sqrt{3}
अब (1) से इनके संगत y के मान होंगेः
जब x=2-\sqrt{3} \\ y=\frac{1-(2-\sqrt{3})}{1+(2-\sqrt{3})^2} \\=\frac{1-2+\sqrt{3}}{1+4+3-4 \sqrt{3}} \\ =\frac{\sqrt{3}-1}{8-4 \sqrt{3}} \\=\frac{\sqrt{3}-1}{4(2-\sqrt{3})} \times \frac{2+\sqrt{3}}{2+\sqrt{3}} \\ =\frac{2 \sqrt{3}+3-2-\sqrt{3}}{4(4-3)} \\ y=\frac{1+\sqrt{3}}{4} \\ (-1,1),\left[(2+\sqrt{3}), \frac{(1-\sqrt{3})}{4}\right],\left[(2-\sqrt{3}), \frac{(\sqrt{3}+1)}{4}\right] \\ \left(\frac{d^{3}y}{d x^3}\right)_{(-1,1)}= \frac{6(-1)^4-24(-1)^3-36(-1)^2+24 \times-1+6}{\left[1+(-1)^2\right]^4} \\ =\frac{6+24-36-24+6}{16} \\ \Rightarrow \left(\frac{d^{3}y}{dx^3}\right)_{(-1,1)}=\frac{-24}{16}=-\frac{3}{2} \neq 0 \\ \left(\frac{d^{3}y}{dx^3}\right)_{\left[(2+\sqrt{3}), \frac{(1-\sqrt{3})}{4}\right]}= \frac{6(2+\sqrt{3})^{4}-24(2+ \sqrt{3})^{3}- 36(2+\sqrt{3})^{2}+24(2+\sqrt{3})+6}{\left[1+(2+\sqrt{3})^{2}\right]^{4}} \\ =\frac{-240-144 \sqrt{3}}{(8+4 \sqrt{3})^4} \\ \Rightarrow\left(\frac{d^3 y}{d x^3}\right)_{\left[(2+\sqrt{3}),\left(\frac{1-\sqrt{3}}{4}\right)\right] }\neq 0
इसी प्रकार \left(\frac{d^3 y}{d x^3}\right)_{\left[(2-\sqrt{3}), \frac{(\sqrt{3}+1)}{4}\right]} \neq 0
अतः (-1,1),\left[(2+\sqrt{3}), \frac{(1-\sqrt{3})}{4}\right],\left[(2-\sqrt{3}), \frac{(\sqrt{3}+1)}{4}\right] नति परिवर्तन बिन्दु हैं।
Example:4. a^2 y^2=x^2\left(a^2-x^2\right)
Solution: a^2 y^2=x^2\left(a^2-x^2\right)
दिए हुए समीकरण को निम्न प्रकार से लिखा जा सकता हैः
y=\frac{x}{a} \sqrt{a^2-x^2} \ldots(1)
समीकरण (1) के दोनों पक्षों का x के सापेक्ष अवकलन करने परः
\frac{dy}{dx}=\frac{1}{a}\left[\sqrt{a^2-x^2}+x\left(\frac{-2 x}{2 \sqrt{a^2-x^2}}\right)\right] \\ =\frac{1}{a}\left[\frac{\left(a^2-x^2\right)-x^2}{\sqrt{a^2-x^2}}\right] \\ \frac{d y}{d x}=\frac{1}{a} \left(\frac{a^2-2 x^2}{\sqrt{a^2-x^2}}\right)
पुनः x के सापेक्ष अवकलन करने परः
\frac{d^2 y}{d x^2} =\frac{1}{a}\left[\frac{\sqrt{a^2-x^2}(-4 x)-\left(a^2-2 x^2\right)\left(\frac{-2 x}{\left(2 \sqrt{a^2-x^2}\right)}\right)}{a^2-x^2}\right] \\ =\frac{1}{a}\left[\frac{-4 x\left(a^2-x^2\right)+ x\left(a^2-2 x^2\right)}{\left(a^2-x^2\right)^{\frac{3}{2}}}\right] \\ =\frac{1}{a}\left[\frac{-4 a^2 x+4 x^3+a^2 x-2 x^3}{\left(a^2-x^2\right)^{\frac{3}{2}}}\right] \\ \Rightarrow \frac{d^2 y}{d x^2} =\frac{1}{a}\left[\frac{2 x^3-3 a^2 x}{\left(a^2-x^2\right)^{\frac{3}{2}}}\right]
पुनः x के सापेक्ष अवकलन करने परः
\frac{d^3 y}{d x^3}=\frac{1}{a}\left[\frac{\left(a^2-x^2\right)^{\frac{3}{2}}\left(6 x^2-3 a^2\right)-\left(2 x^3-3 a^2 x\right)\left(-\frac{3 x}{2}\right) \\ 2\left(a^2-x^2\right)^{\frac{1}{2}}}{\left(a^2-x^2 \right)^{3}} \right] \\ =\frac{\left(a^2-x^2\right)^{\frac{1}{2}}}{a}\left[\frac{\left(a^2-x^2\right)\left(6 x^2-3 a^2\right) +3 x\left(2 x^3-3 a^2 x\right)}{\left(a^2-x^2\right)^3}\right] \\ =\frac{1}{a}\left[\frac{6 a^2 x^2-3 a^4-6 x^4+3 a^2 x^2+6 x^4-9 a^2 x^2}{\left(a^2-x^2\right)^{\frac{5}{2}}}\right] \\ =\frac{1}{a}\left[\frac{6 a^2 x^2-3 a^4}{\left(a^2-x^2\right)^{\frac{5}{2}}}\right] \\ \Rightarrow \frac{d^{3}y}{dx^3} =\frac{1}{a} \left[\frac{6 a^2 x^2-3 a^4}{\left(a^2-x^2\right)^{\frac{5}{2}}}\right]
नति परिवर्तन बिन्दु के लिएः
\frac{d^2 y}{d x^2}=0 तथा \frac{d^3 y}{d x^3} \neq 0
अब \frac{d^2 y}{d x^2}=0 सेः
\frac{1}{a}\left[\frac{2 x^3-3 a^2 x}{\left(a^2-x^2\right)}\right]=0 \Rightarrow x\left(2 x^2-3 a^2\right)=0 \\ x=0, \pm \sqrt{\frac{3}{2}} a, x= \pm \sqrt{\frac{3}{2}} a वास्तविक मान के लिए असंभव है |
अब (1) से इनके संगत y के मान होंगेः
y_{(0,0)}=0 \\ \left(\frac{d^3 y}{d x^3}\right)_{(0,0)}=\frac{1}{a}\left[\frac{6 a^2(0)^2-3 a^4}{\left(a^2-0^2\right)^{\frac{5}{2}}}\right] \\ \Rightarrow\left(\frac{d^3 y}{d x^3}\right)_{(0,0)}=-\frac{3 a^3}{a^5}=-\frac{3}{a^2} \neq 0
अतः (0,0) नति परिवर्तन बिन्दु हैं।
Example:5. x^2 y=a^2(x-y)
Solution: x^2 y=a^2(x-y)
दिए हुए समीकरण को निम्न प्रकार से लिखा जा सकता हैः
x^2 y=a^2 x-a^2 y \\ \Rightarrow x^2 y+a^2 y=a^2 x \\ \Rightarrow y\left(a^2+x^2\right)=a^2 x \\ \Rightarrow y=\frac{a^2 x}{a^2+x^2} \ldots(1)
समीकरण (1) के दोनों पक्षों का x के सापेक्ष अवकलन करने परः
\frac{d y}{d x} =a^2\left[\frac{\left(a^2+x^2\right) \cdot 1-x \cdot 2 x}{\left(a^2+x^2\right)^2} \right] \\ =a^2\left[\frac{a^2+x^2-2 x^2}{\left(a^2+x^2\right)^2}\right] \\ \frac{d y}{d x}=a^2 \frac{\left(a^2-x^2 \right)}{\left(a^2+x^2\right)^2}
पुनः x के सापेक्ष अवकलन करने परः
\frac{d^{2}y}{d x^2}=a^2\left[\frac{\left(a^2+x^2\right)^2(-2 x)-\left(a^2-x^2\right) \cdot 2\left(a^2+ x^2\right)\cdot 2x}{\left(a^2+x^2\right)^4 }\right] \\ =a^2\left[\frac{\left(a^2+x^2\right) \left\{\left(a^2+ x^2\right)(-2 x)-4 x\left(a^2-x^2\right)\right\}}{\left(a^2+x^2\right)^4}\right] \\ =\frac{a^2\left(-2 a^2 x-2 x^3-4 a^2 x+4 x^3\right)}{\left(a^2+x^2\right)^3} \\ \Rightarrow \frac{d^2 y}{d x^2} =\frac{a^2\left(2 x^3-6 a^2 x\right)}{\left(a^2+x^2\right)^3}
पुनः x के सापेक्ष अवकलन करने परः
\frac{d^3 y}{d x^3}=a^2\left[\frac{\left(a^2+x^2\right)^3\left(6 x^2-6 a^2\right)-\left(2 x^3-6 a^2 x\right) 3\left(a^2+x^{2}\right)^2 \cdot 2 x}{\left(a^2+x^2\right)^6}\right] \\=a^2\left(a^2+x^2\right)^2 \left[\frac{\left(a^2+x^2\right)\left(6 x^2-6 a^2\right)-\left(2 x^3-6a^{2} x\right) \cdot 6 x}{\left(a^2+ x^2\right)^6}\right] \\ =\frac{a^2\left(6 a^2 x^2-6 a^4+6 x^4-6 a^2 x^2-12 x^4+36 a^2 x^2\right)}{\left(a^2+x^2\right)^4} \\ \Rightarrow \frac{d^3 y}{d x^3}=\frac{a^2\left(-6 x^4+36 a^2 x^2-6 a^4\right)}{\left(a^2+x^2\right)^4}
नति परिवर्तन बिन्दु के लिएः
\frac{d^2 y}{d x^2}=0 तथा \frac{d^3 y}{d x^3} \neq 0
अब \frac{d^2 y}{d x^2}=0 सेः
\frac{a^2\left(2 x^3-6 a^2 x\right)}{\left(a^2+x^2\right)^3}=0 \\ \Rightarrow 2 x^3-6 a^2 x=0 \\ \Rightarrow x\left(2 x^2-6 a^2\right)=0 \Rightarrow x=0, \pm \sqrt{3} a
अब (1) से इनके संगत y के मान होंगेः
जब x=0 तो y=0
जब x=\sqrt{3}a तो y=\frac{a^2(\sqrt{3} a)}{a^2+3 a^2}=\frac{\sqrt{3}}{4} a
जब x=-\sqrt{3}a तो y=\frac{a^2(-\sqrt{3} a)}{a^2+3 a^2}=-\frac{\sqrt{3}}{4} a \\ (0,0)\left(\sqrt{3} a, \frac{\sqrt{3}}{4} a\right)\left(-\sqrt{3} a,-\frac{\sqrt{3}}{4} a\right) \\ \left(\frac{d^{3}y}{d x^3} \right)_{(0,0)}=\frac{a^2\left(-6 a^4\right)}{a^8}=-\frac{6}{a^2} \neq 0 \\ \left(\frac{d^3 y}{d x^3} \right)_{\left(\sqrt{3} a, \frac{\sqrt{3}a}{4} \right)}=a^2\left[\frac{-6\left(\sqrt{3} a\right)^4+36 a^2 \left(\sqrt{3} a\right)^2-6 a^4}{\left(a^2+3 a^2\right)^4}\right] \\ =a^2\left[\frac{-54 a^4+108 a^4-6 a^4}{256 a^8}\right] \\ \Rightarrow\left(\frac{d^3 y}{d x^{3}}\right)_{\left(\sqrt{3} a, \frac{\sqrt{3}a}{4} \right)}=\frac{3}{16 a^2} \neq 0 \\ \left(\frac{d^3 y}{d x^3}\right)_{\left(\sqrt{3} a,-\frac{\sqrt{3}a}{4}\right)}=a^2\left[\frac{-6(-\sqrt{3} a)^4+36 a^2(-\sqrt{3} a)^2-6 a^4}{\left(a^2+3 a^2\right)^4}\right] \\ \Rightarrow\left(\frac{d^3 y}{d x^3}\right)_{\left(\sqrt{3} a,-\frac{\sqrt{3}a}{4}\right)}=\frac{3}{16 a^2} \neq 0
अतः (0,0),\left(-\sqrt{3} a,\frac{\sqrt{3}}{4} a\right),\left(-\sqrt{3} a,-\frac{\sqrt{3} a}{4}\right) नति परिवर्तन बिन्दु हैं।
Example:6. y=3 x^4-4 x^3+1
Solution: y=3 x^4-4 x^3+1 \ldots(1)
समीकरण (1) के दोनों पक्षों का x के सापेक्ष अवकलन करने परः
\frac{d y}{d x}=12 x^3-12 x^2
पुनः x के सापेक्ष अवकलन करने परः
\frac{d^2 y}{d x^2}=36 x^2-24 x
पुनः x के सापेक्ष अवकलन करने परः
\frac{d^3 y}{d x^3}=72 x-24
नति परिवर्तन बिन्दु के लिएः
\frac{d^2 y}{d x^2}=0 तथा \frac{d^3 y}{d x^3} \neq 0
अब \frac{d^2 y}{d x^2}=0 सेः
36 x^2-24 x=0 \\ \Rightarrow 12 x(3 x-2)=0 \\ \Rightarrow x=0, \frac{2}{3}
अब (1) से इनके संगत y के मान होंगेः
x=0 तो y=0
x=\frac{2}{3} तो y=3\left(\frac{2}{3}\right)^4-4\left(\frac{2}{3}\right)^3+1=\frac{16}{27}-\frac{32}{27}+1 \\ \Rightarrow y=\frac{16-32+27}{27}=\frac{11}{27} \\ (0,0)\left(\frac{2}{3}, \frac{11}{27}\right) \\ \left(\frac{d^3 y}{d x^3}\right)_{(0,0)}=72(0)-24=-24 \neq 0 \\ \left(\frac{d^3 y}{d x^3} \right)_{\left(\frac{2}{3}, \frac{11}{27}\right)}=72 \times \frac{2}{3}-24=48-24=24 \neq 0
अतः (0,0),\left(\frac{2}{3}, \frac{11}{27}\right) नति परिवर्तन बिन्दु हैं।
Example:7. x=(\log y)^3
Solution: x=(\log y)^3 \ldots(1)
समीकरण (1) के दोनों पक्षों का y के सापेक्ष अवकलन करने परः
\frac{d x}{d y}=\frac{3(\log y)^2}{y}
पुनः y के सापेक्ष अवकलन करने परः
\frac{d^2 x}{d y^2} =3\left[\frac{y \cdot \frac{ 2 \log y}{y}-(\log y)^2 \cdot 1}{y^2}\right] \\ \Rightarrow \frac{d^2 x}{dy^2} =3\left[\frac{2 \log y-(\log y)^2}{y^2}\right]
पुनः y के सापेक्ष अवकलन करने परः
\frac{d^{3}y}{d y^3}=\frac{3\left[y^2\left\{\frac{2}{y}-\frac{2 \log y}{y}\right\}-\left\{ 2 \log y-(\log y)^2 \right\}\cdot 2 y\right]}{y^4} \\ = \frac{3 y\left[2-2 \log y-4 \log y+2(\log y)^2\right]}{y^4} \\ \Rightarrow \frac{d^3 y}{d y^3} =\frac{3\left[2-6 \log y+2(\log y)^2\right]}{y^3}
नति परिवर्तन बिन्दु के लिएः
\frac{d^2 x}{d y^2}=0 तथा \frac{d^3 x}{d y^3} \neq 0
अब \frac{d^2 x}{d y^2}=0 सेः
\frac{3\left[2 \log y-(\log y)^2\right]}{y^2}=0 \\ \Rightarrow (\log y)(2-\log y)=0 \\ \Rightarrow \log y=0 \Rightarrow y=1 \\ 2-\log y=0 \Rightarrow \log y=2 \Rightarrow y=e^2
अब (1) से इनके संगत y के मान होंगेः
जब y=1 तो x=\left(\log 1\right)^3=0
जब y=e^2 तो x=\left(\log e^2\right)^3=\left(2 \log _e e\right)^3=8 \\ (0,1),\left(8, e^2\right) \\ \left(\frac{d^3 x}{d y^3}\right)_{(0,1)}=\frac{3\left[2-6 \log 1+2(\log 1)^2\right]}{1^3} \\ \Rightarrow \left(\frac{d^{3}x}{d y^3}\right)_{(0,1)}=6 \neq 0 \\ \left(\frac{d^3 x}{dy^3}\right)_{\left(8, e^2\right)} =\frac{3\left[2-6 \log e^2+2\left(\log e^2\right)^2\right]}{e^6} \\ =\frac{3(2-12+8)}{e^6} \\ \Rightarrow \left(\frac{d^3 x}{d y^3}\right)_{\left(8, e^2\right)}=-\frac{6}{e^6} \neq 0
अतः (0,1),\left(8, e^2\right) नति परिवर्तन बिन्दु हैं।
Example:8.सिद्ध कीजिए कि वक्र y^2=(x-a)^2(x-b) के नति-परिवर्तन बिन्दु 3x+a=4b रेखा पर स्थित हैं।
(Show that the point of inflexion of the curve y^2=(x-a)^2(x-b) lie on the line 3x+a=4b.)
Solution: y^2=(x-a)^2(x-b) \\ \Rightarrow y=(x-a) \sqrt{x-b} \ldots(1)
समीकरण (1) का x के सापेक्ष अवकलन करने परः
\frac{d y}{d x} =\frac{x-a}{2 \sqrt{x-b}}+\frac{\sqrt{x-b}}{1}(1) \\ =\frac{(x-a)+2(x-b)}{2 \sqrt{x-b}} \\ \Rightarrow \frac{d y}{d x} =\frac{3 x-a-2 b}{2 \sqrt{x-b}} \\ \frac{d^2 y}{d x^2} =\frac{1}{2} \left[ \frac{\sqrt{x-b} \cdot 3-(3 x-a-2 b) \cdot \frac{1}{2 \sqrt{x-b}}}{x-b}\right] \\ =\frac{1}{2}\left[\frac{6(x-b)-(3 x-a-2 b)}{2(x-b)^{\frac{3}{2}}}\right] \\ =\frac{1}{4} \frac{(3 x+a-4 b)}{(x-b)^{\frac{3}{2} }}
नति परिवर्तन बिन्दु के लिएः \frac{d^2 y}{d x}=0 \\ \Rightarrow 3 x+a-4 b=0
जब 3x+a=4b तब \frac{d^3 y}{dx^3} \neq 0
अतः नति परिवर्तन बिन्दु रेखा 3x+a=4b पर स्थित है।
Example:9.सिद्ध कीजिए कि वक्र r=b \theta^n के नति-परिवर्तन बिन्दु r=b\{-n(n+1)\}^{\frac{n}{2}} पर हैं।
(Show that the point of inflexion on the curve r=b \theta^n are given by r=b\{-n(n+1)\}^{\frac{n}{2}})
Solution: x=b \theta^n \ldots(1) \\ \theta के सापेक्ष अवकलन करने परः
\frac{dr}{d \theta}=b n \theta^{n-1}
पुनः \theta के सापेक्ष अवकलन करने परः
\frac{d^2 r}{d \theta^2}=b n(n-1) \theta^{n-2}
ध्रुवीय वक्रों के लिए नति परिवर्तन बिन्दु का प्रतिबन्धः
r^2+2\left(\frac{d r}{d \theta}\right)^2-r \frac{d^2 r}{d \theta^2}=0 \\ \\ \Rightarrow r^2+2 b^2 n^2 \theta^{2 n-2}-r \cdot b n(n-1) \theta^{n-2}=0 \\ r=b \theta^{n} \Rightarrow \theta=\left(\frac{r}{b}\right)^{\frac{1}{n}} रखने परः
r^2+2 b^2 n^2\left(\frac{r}{b}\right)^{\frac{2 n-2}{n}}-r b n(n-1)\left(\frac{r}{b}\right)^{\frac{n-2}{n}}=0 \\ \Rightarrow r^2+2 b^{2-\left(\frac{2 n-2}{n}\right)}n^2 r^{\frac{2 n-2}{n}}-n(n-1) b^{1-\frac{n-2}{n}} r^{1+\frac{n-2}{n}}=0 \\ \Rightarrow r^2+2 b^{\frac{2}{n}} n^2 r^{\frac{2 n-2}{n}}-\left(n^2-n\right) b^{\frac{2}{n}} r^{\frac{2 n-2}{n}}=0 \\ \Rightarrow r^2= -2 b^{\frac{2}{n}} n^2 r^{\frac{2 n-2}{n}}+n^2 b^{\frac{2}{n}} r^{\frac{2 n-2}{n}}-n b^{\frac{2}{n}} r^{\frac{2 n-2}{n}} \\ \Rightarrow r^2=-b^{\frac{2}{n}} n(n+1) r^{\frac{2 n-2}{2}} \\ \Rightarrow r^{2-\frac{2 n-2}{n}}=-b^{\frac{2}{n}} n(n+1) \\ \Rightarrow r^{\frac{2}{n}}=-b^{\frac{2}{n}} n(n+1) \\ \Rightarrow r=b\{-n(n+1)\}^{\frac{n}{2}}
अतः नति-परिवर्तन बिन्दु उपर्युक्त पर स्थित है।
Example:10.वक्र r\left(\theta^2-1\right)=a \theta^2 के लिए सिद्ध कीजिए कि नति-परिवर्तन बिन्दु r=\frac{3a}{2} पर हैं।
(Prove that for the curve r\left(\theta^2-1\right)=a \theta^2,there is a point of inflexion at the point,where r=\frac{3a}{2})
Solution: r\left(\theta^2-1\right)=a \theta^2 \cdots(1) \\ r=\frac{a \theta^2}{\theta^2-1} \\ \theta के सापेक्ष अवकलन करने परः
\frac{d r}{d \theta}=a\left[\frac{\left(\theta^2-1\right) \cdot 2 \theta-\theta^2-2 \theta}{\left(\theta^2-1\right)^2}\right] \\ =a\left[\frac{2 \theta^3-2 \theta-2 \theta^3}{\left(\theta^2-1\right)^2}\right] \\ \Rightarrow \frac{d r}{d \theta} =-\frac{2 a \theta}{\left(\theta^2-1\right)^2}
पुनः \theta के सापेक्ष अवकलन करने परः
\frac{d^2 r}{d \theta^2} =-2 a\left[\frac{\left(\theta^2-1\right)^2 \cdot 1-\theta \cdot 2\left( \theta^2-1\right) \cdot 2 \theta}{\left(\theta^2-1\right)^4}\right] \\ =-2 a\left(\theta^2-1\right)\left[ \frac{\theta^2-1-4 \theta^2}{\left(\theta^2-1\right)^4}\right] \\ \Rightarrow \frac{d^2 r}{d \theta^2} =\frac{2 a\left(1+3 \theta^2\right)}{\left(\theta^2-1\right)^3}
ध्रुवीय वक्रों के लिए नति-परिवर्तन बिन्दु का प्रतिबन्धः
r^2+2\left(\frac{d r}{d \theta}\right)^2-r \frac{d^2 r}{d \theta^2}=0 \\ \Rightarrow r^2+2\left[-\frac{2 a \theta}{\left(\theta^2-1\right)^2}\right]^2-r \cdot \frac{2 a\left(1+3 \theta^2\right)}{\left(\theta^2-1\right)^3}=0 \\ \Rightarrow \frac{a^{2} \theta^4 }{\left(\theta^2-1\right)^2}+\frac{8 a^2 \theta^2}{\left(\theta^2-1\right)^4}-\frac{a \theta^2}{\left(\theta^2-1\right)} \cdot \frac{2 a\left(1+3 \theta^2 \right)}{\left(\theta^2-1\right)^3}=0 \\ \Rightarrow \frac{a^2 \theta^4\left(\theta^2-1\right)^2 +8 a^2 \theta^2-2 a^2 \theta^2-6 a^2 \theta^4}{\left(\theta^2-1\right)^4}=0 \\ \Rightarrow a^2 \theta^8-2 a^2 \theta^6+a^2 \theta^4+6 a^2 \theta^2-6 a^2 \theta^4=0 \\ \Rightarrow a^2 \theta^2\left( \theta^{6}- 2 \theta^4-5 \theta^2+6\right)=0 \\ \Rightarrow \theta^6+2 \theta^4-4 \theta^4-8 \theta^2+3 \theta^2+6=0 \\ \Rightarrow \theta^4\left(\theta^2+2\right)-4 \theta^2 \left(\theta^2 +2\right)+3\left(\theta^2+2\right)=0 \\ \Rightarrow \left(\theta^2+2\right)\left(\theta^4-4 \theta^2+ 3\right)=0 \\ \Rightarrow\left(\theta^2+2\right)\left[\theta^4-3 \theta^2-\theta^2+3\right]=0 \\ \Rightarrow \left(\theta^2+2\right)\left[\theta^2\left(\theta^2-3\right)-1\left(\theta^2-3\right)\right] =0 \\ \Rightarrow \left(\theta^2+2\right)\left(\theta^2-1\right)\left(\theta^2-3\right)=0 \\ \Rightarrow \theta^2+2=0, \theta^2-1=0 सम्भव नहीं है।अतः \theta^2-3=0 \\ \theta^2=3 \\ \theta^2=3 समीकरण (1) में रखने परः r(3-1)=a(3) \\ \Rightarrow r=\frac{3 a}{2}
अतः नति-परिवर्तन बिन्दु r=\frac{3 a}{2} पर स्थित हैं।
उपर्युक्त उदाहरणों के द्वारा कलन में नति परिवर्तन बिन्दु (Point of Inflexion in Calculus),अवकलन गणित में नति परिवर्तन बिन्दु (Point of Inflexion in Differential Calculus) को समझ सकते हैं।
3.कलन में नति परिवर्तन बिन्दु पर आधारित सवाल (Questions Based on Point of Inflexion in Calculus):
निम्नलिखित वक्रों के नति-परिवर्तन बिन्दु ज्ञात कीजिएः
(Find the point of inflexion for the following curves):
(1.) y\left(a^2+x^2\right)=x^3
(2.) y=\frac{1}{1+x^2}
उत्तर (Answers):(1.)(0,0),\left(\sqrt{3} a, \frac{3 \sqrt{3}a}{4} \right) तथा \left(\sqrt{3} a,-\frac{3 \sqrt{3}a}{4}\right)
(2.)\left(\frac{1}{\sqrt{3}}, \frac{3}{4}\right) \left(-\frac{1}{\sqrt{3}}, \frac{3}{4}\right)
उपर्युक्त सवालों को हल करने पर कलन में नति परिवर्तन बिन्दु (Point of Inflexion in Calculus),अवकलन गणित में नति परिवर्तन बिन्दु (Point of Inflexion in Differential Calculus) को ठीक से समझ सकते हैं।
Also Read This Article:-Intersection of Curve and Asymptotes
4.कलन में नति परिवर्तन बिन्दु (Frequently Asked Questions Related to Point of Inflexion in Calculus),अवकलन गणित में नति परिवर्तन बिन्दु (Point of Inflexion in Differential Calculus) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्नः
प्रश्न:1.वक्र की अवतलता से क्या तात्पर्य है? (What Do You Mean by Concavity of Curve?):
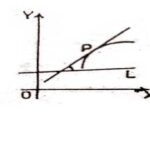
उत्तर:चित्र में बिन्दु P पर खींचे गए स्पर्श रेखा तथा स्थिर रेखा L के बीच बने न्यून कोण (Acute Angle) में बिन्दु P के दोनों ओर फैला हुआ पर्याप्त छोटा चाप पूर्ण रूप से भीतर है।ऐसी स्थिति में बिन्दु P पर वक्र को रेखा L के सापेक्ष अवतल (Concave) कहते हैं।
प्रश्न:2.वक्र की उत्तलता से क्या तात्पर्य है? (What Do You Mean by Convexity of Curve?):
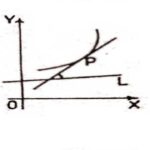
उत्तर:चित्र में बिन्दु P पर खींचे गए स्पर्श रेखा तथा स्थिर रेखा L के बीच बने न्यून कोण (acute angle) से बिन्दु P के दोनों ओर फैला हुआ पर्याप्त छोटा चाप पूर्ण रूप से बाहर है।ऐसी स्थिति में बिन्दु P पर वक्र को रेखा L के सापेक्ष उत्तल (Convex) कहते हैं।
प्रश्न:3.नति-परिवर्तन बिन्दु किसे कहते हैं? (What is Point of Inflexion?):

उत्तर:चित्र में बिन्दु P पर सरल रेखा L के सापेक्ष एक ओर अवतल तथा दूसरी ओर उत्तल है।ऐसे बिन्दु P को नति-परिवर्तन बिन्दु (point of inflexion) कहते हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा कलन में नति परिवर्तन बिन्दु (Point of Inflexion in Calculus), अवकलन गणित में नति परिवर्तन बिन्दु (Point of Inflexion in Differential Calculus) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Point of Inflexion in Calculus
कलन में नति परिवर्तन बिन्दु
(Point of Inflexion in Calculus)
Point of Inflexion in Calculus
कलन में नति परिवर्तन बिन्दु (Point of Inflexion in Calculus) को जानने के लिए वक्रों की
अवतलता (Concavity),उत्तलता (Convexity),नति परिवर्तन बिन्दु को जानना आवश्यक है।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.








