Perfect Number Day on 28th June
1.28 जून को परिपूर्ण संख्या दिवस (Perfect Number Day on 28th June),28 जून को परिपूर्ण संख्या दिवस का गणित अवकाश मनाएं (Celebrate The Mathematics Holiday Of Perfect Number Day on 28th June):
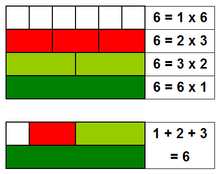
- 28 जून को परिपूर्ण संख्या दिवस (Perfect Number Day on 28th June) प्रतिवर्ष समस्त विश्व में मनाया जाता है।आइए जानते हैं परिपूर्ण संख्या तथा परिपूर्ण दिवस क्या है? परिपूर्णता एक अप्राप्य खोज है जिसके लिए हम सभी प्रयास करते हैं।लेकिन गणित में किसी संख्या को परिपूर्ण संख्या होने के लिए एक विशिष्ट परिभाषा है जिसे कुछ चुनिंदा संख्याएँ ही पूरा कर सकती हैं।कोई संख्या तभी परिपूर्ण हो सकती है जब उसके सभी गुणनखंड (सर्व सम्भव गुणनखंड) 1 को शामिल करते हुए परंतु स्वयं को छोड़कर जोड़ने पर उस संख्या के बराबर आते हैं।उदाहरण के लिए 6 परिपूर्ण संख्या है क्योंकि इसके सर्व सम्भव गुणनखंड 1,2,3 तथा 6 हैं।6 को छोड़कर सभी का योग 1+2+3=6 आता है।इसी प्रकार 28 भी परिपूर्ण संख्या है:14,7,4,2 और 1 का योग 28 है। लेकिन परिपूर्ण संख्याएं बिल्कुल भी सामान्य नहीं है।1 मिलियन से कम केवल दो ओर परिपूर्ण संख्याएं हैं:496, 8128 हैं।
- कंप्यूटेशनल (कंप्यूटर के द्वारा) एक समर्पित विश्वव्यापी प्रयास के साथ पूर्ण संख्याएं ज्ञात की गई है।फिर भी हमारे समय के कुछ महानतम गणितीय प्रश्नों से उनका गहरा संबंध है।जबकि कुछ लोग 28 जून (6/28) को ताऊ दिवस (Tau Day) के रूप में याद कर सकते हैं।इस तथ्य के उपलक्ष्य में कि \tau=2\pi,आप केवल उन संख्याओं के उत्सव में शीर्ष (टाॅप) पर नहीं हो सकते जो वास्तव में परिपूर्ण है।
- 28 जून, 6 और 28 के कैलेंडर में कुछ बहुत ही खास गुण है जो एक उत्सव के योग्य है।दरअसल जब तक आपका जन्म वर्ष 496 में नहीं हुआ या वर्ष 8128 के समय तक आपके कैलेंडर पर केवल 6 और 28 परिपूर्ण संख्याएँ दिखाई देगी।
यदि आप किसी संख्या के उसके सभी भाजकों में जोड़ सकते हैं और खोज सकते हैं कि आपकी संख्या परिपूर्ण है या नहीं।आप देख सकते हैं कि अधिकांश संख्याएँ बिल्कुल भी परिपूर्ण नहीं है।वे या तो जोड़ में अधिक है या कम है।
पहली कुछ गणनीय संख्याएँ ज्यादातर में कमी है लेकिन 6 परिपूर्ण संख्या है।सबसे पहले खोजी जानेवाली और सबसे आसान संख्या है।
- यदि आप किसी भी संख्या के सभी धनात्मक गुणनखंडों को जोड़ते हैं जिसमें संख्या स्वयं शामिल नहीं है तो आपको जो संख्या प्राप्त होगी वह मूल संख्या से छोटी, बड़ी और उसके बिल्कुल बराबर होगी।
- यदि आप स्वयं को छोड़कर सभी गुणनखण्डों को जोड़ते हैं और एक संख्या प्राप्त करते हैं तो जो आपके द्वारा शुरू की गई मूल संख्या से कम है तो हम उसे अपूर्ण संख्या कहते हैं।सभी अभाज्य संख्याएँ अधिकतम रूप से कम होती हैं क्योंकि उसके गुणनखण्ड 1 और स्वयं संख्या होती है।और 2 (4,8,16,32 आदि) की सभी घातों में न्यूनतम कमी होती है।जैसे 2 के गुणनखण्ड 1 जो 1 कम है।4 के गुणनखण्ड 1,2 का योग 1+2=3 जो 4 से 1 कम है।इसी प्रकार 8 के गुणनखंड (स्वयं को छोड़कर) 1,2,4 है जिनका योग 1+2+4=7 जो 8 से 1 कम है।
- दूसरी और आप स्वयं को छोड़कर किसी संख्या के सभी गुणनखंडों को जोड़ सकते हैं और मूल संख्या से बड़ी संख्या प्राप्त कर सकते हैं।ऐसी संख्या बहुत अधिक है।आप ऊपर दी गई तालिका से देख सकते हैं और सोच सकते हैं कि प्रचुर संख्याएँ (Abundant) दुर्लभ है।लेकिन 18,20,24,30,36 और कई ओर प्रचुर मात्रा में।जैसे-जैसे आप बड़ी और बड़ी संख्याओं को देखना शुरू करते हैं वे काफी हैं।18 के गुणनखण्ड 1,2,3,6,9 हैं जिनका योग 1+2+3+6+9=21 है 18 से अधिक है।इसी प्रकार की प्रचुर संख्याएँ (Abundant) ऊपर दी गई है।
- प्रथम चार परिपूर्ण संख्याओं के गुणनखण्ड में यदि आप संख्या स्वयं को हटा देते हैं तो अन्य सभी गुणनखण्ड (या भाजक) विचाराधीन संख्या के योग बन जाते हैं जो परिपूर्ण संख्या के मानदंड को पूरा करते हैं।
- लेकिन बिल्कुल परिपूर्ण संख्या जिसे यूक्लिड ने कहा है,दुर्लभ है।1000 से अधिक वर्षों से केवल 4 परिपूर्ण संख्याएं ज्ञात थी।
आप इन नंबरों को देख सकते हैं जो परिपूर्ण होते हैं और यहां एक पैटर्न देखना शुरु करते हैं कि इन नंबरों को कैसे तोड़ा जा सकता है वे दो को किसी घात से गुणा करके करने का परिणाम है,आइए इस अभाज्य संख्या को X कहते हैं।दिलचस्प बात यह है कि जिस अभाज्य संख्या से आप गुणा कर रहे हैं वह हमेशा 2^X के दोगुने से कम के बराबर होती है।
पहले चार परिपूर्ण संख्याओं को तोड़ने के विभिन्न तरीकों से एक सूचक पैटर्न का पता चलता है कि वह कैसे उत्पन्न हो सकती है।
- इसका एक अच्छा कारण है कि 2 की सभी घातें जैसे संख्याएँ 2,4,8,16,32 आदि न्यूनतम रूप से परिपूर्ण संख्या से 1 कम है।साथ ही सभी अभाज्य संख्याएं अधिकतम न्यून होती हैं जहां उनके गुणनखण्ड 1 और स्वयं होते हैं।इसका मतलब है कि दो और अभाज्य संख्याओं की घातों के संभावित संयोजन,न्यूनतम और अधिकतम रूप से कम संख्याएं हैं जिनके पास स्वयं को परिपूर्ण होने का मौका है।
- हालांकि संख्याओं का प्रत्येक न्यूनतम और अधिकतम कमी वाला संयोजन आपको एक परिपूर्ण संख्या नहीं देता है।यदि आप परिपूर्ण संख्याओं के “प्राइम फैक्टर ब्रेकडाउन” को देखते हैं तो ऐसा लगता है कि उन्हें उत्पन्न (जनित) करने के लिए एक पैटर्न है।वास्तव में आप अनुमान लगा सकते हैं कि पैटर्न कुछ इस प्रकार है:
- हमारे द्वारा ज्ञात अभाज्य संख्याओं के आधार पर आप सभी परिपूर्ण संख्याओं के लिए जिस पैटर्न का अनुमान लगा सकते हैं,वह आपको केवल परिपूर्ण संख्या दे सकता है।इनमें से कई अभाज्य संख्या नहीं हैं और परिपूर्ण संख्याएँ उत्पन्न नहीं करती हैं।
- आखिरकार पहली चार अभाज्य संख्याएँ 2,3,5,7 है।इसलिए अगर हम इस सूत्र में अभाज्य संख्याएँ जोड़ते हैं:जहाँ n एक अभाज्य संख्या है और सूत्र [2^{n-1}\left(2^{n}-1\right)] से हम परिपूर्ण संख्याएँ बनाना शुरू करेंगे। यह सभी अभाज्य संख्याओं 2,3,5,7,11,13,17,19,23,29,31,37 इत्यादि के लिए कार्य करता है।
- जैसा कि यह पता चला है कि यह उम्मीदवार को परिपूर्ण संख्याएँ उत्पन्न करने का शानदार तरीका है लेकिन जरूरी नहीं है कि स्वयं परिपूर्ण संख्याएं हों। वास्तव में सभी ज्ञात परिपूर्ण संख्याएँ इस सूत्र का पालन करती है जहां n एक अभाज्य संख्या है और [2^{n-1}\left(2^{n}-1\right)] आपको एक परिपूर्ण संख्या देता है।लेकिन यह सच नहीं है कि सभी अभाज्य संख्याएं एक परिपूर्ण संख्या उत्पन्न करती है।यह केवल चुनिंदा अभाज्य संख्याओं के लिए कार्य करता है।
पहली पांच परिपूर्ण संख्याएँ और कुछ दिलचस्प संख्यात्मक गुण जो उन्हें उत्पन्न करने के संदर्भ में प्रदर्शित करती है। - पांचवी पूर्ण संख्या होनी चाहिए 2096128 [2^{10}\left(2^{11}-1\right)] है।वास्तव में यह एक प्रचुर संख्या (abundant) है।यह सिर्फ यादृच्छिक (random) नहीं है,इसका कारण है।2,3,5 और समीकरण के भाग (part) 2^{n} -1 ने अभाज्य संख्याएँ 3,7,31 और 127 दी है।2096128 एक परिपूर्ण संख्या नहीं है क्योंकि कोष्टक में वह \left(2^{11}-1\right)] (जो कि 2047 है) अपने आपमें अभाज्य नहीं है।2047 का गुणनखंड किया जा सकता है जो 23×89 है और इसलिए यह अभाज्य नहीं है। इस वजह से संख्या 2096128 या [2^{10}\left(2^{11}-1\right)] भी परिपूर्ण संख्या नहीं है।
- सूत्र [2^{n-1}\left(2^{n}-1\right)] लेना पर्याप्त नहीं है क्योंकि n केवल एक नियमित अभाज्य संख्या है।आपको यह सुनिश्चित करने की जरूरत है कि फाॅर्मूला में \left(2^{n}-1\right) आपको एक अभाज्य संख्या देता है।इस प्रकार का प्राइम जहाँ n प्राइम (अभाज्य) है और \left(2^{n}-1\right) भी प्राइम है इसे मेर्सन प्राइम (Mersenne Prime) कहा जाता है।इसका नाम सैंकड़ों साल पहले इनका अध्ययन करने वाले भिक्षु [भिक्षु मारिन मेर्सन (Monk Marin Mersenne)] के नाम पर (2018) में रखा गया है।उनमें से केवल 50 ही अस्तित्व में है और वे आकार में बहुत जल्दी बढ़ती है।
- 50 मेर्सन प्राइम (Mersenne Primes) में वर्तमान में सबसे बड़ी 2^{77232917}-1 है जिसमें 23 मिलियन (Million) से अधिक अंक है।यह अनिश्चित है कि 50वां मेर्सन प्राइम है क्योंकि 42 मेर्सन प्राइम को क्रम में होने के लिए सत्यापित किया गया है।Mersenne Primes के बड़े उपयुक्त अन्तराल है।इससे मेल खाने वाली परिपूर्ण संख्या में 46,498,849 अंक होते हैं और इसे प्रदर्शित करने के लिए लगभग 16000 मुद्रित पृष्ठ लगेंगे।
- मानो या न मानो यह ऐसी खोज है जिसमें आप में से कंप्यूटर प्रेमी भाग ले सकते हैं।महान इंटरनेट प्राइम सर्च करने के लिए नगद पुरस्कार शामिल है।
- यदि आप थोड़ा अनुमान (conjectured) चाहते हैं कि वर्तमान रिकाॅर्ड को कैसे तोड़ा जाए तो यहां एक मजेदार जानकारी है जिस पर आप विचार कर सकते हैं।संख्या 3,7 और 127 (पहली,दूसरी और चौथी मेर्सन प्राइम) के अलावा 170,141,183,460,469,231,731,687,303,715,884,105,727 संख्या एक मेर्सन प्राइम भी है (12वां) इसमें 39 अंक हैं।इसका मतलब है कि 6,28 और 8128 के अलावा निम्नलिखित संख्या भी बिल्कुल परिपूर्ण संख्या है:14,474,011,154,664,524,427,946,373,126,085,988,481,573,677,491,474,835,889,066,354,349,131,199,152,128
- कई लोगों ने अनुमान लगाया है कि (2^{170,141,183,460,469,231,731,687,303,715,884,105,727}–1) अर्थात् (2^{170,141,183,460,469,231,731,687,303,715,884,105,727}–1) एक मेर्सन प्राइम भी है।क्या आप तैयार हैं 10^{37} से भी अधिक अंक।
- मेर्सन प्राइम में एक आकर्षक पैटर्न है जिसे सैकड़ों साल पहले यूलर (Leonhard Euler) ने नोट किया था।यह हमें सभी के सबसे बड़े Mersenne Prime तक ले जा सकता है और यह हमें एक रास्ता दे सकता है।यह पैटर्न स्वेच्छ ढंग से जारी रहता है,बड़े Mersenne Prime उत्पन्न (जनित) करने के लिए।
- इस पैटर्न का पालन करने वाले पहले चार नंबर मेर्सन प्राइम है लेकिन पांचवा? और इसके अलावा, क्या यह असीमित संख्या में Mersenne Prime उत्पन्न करने का एक वैद्य तरीका है? यह पैटर्न जरूरी नहीं कि पकड़ में आए।मेर्सन प्राइम के कई उदाहरण हैं जैसेः8191, 131071 और 524287 जहाँ 2^{n}-1,\left(2^{8191}-1\right) स्वयं मेर्सन प्राइम नहीं है।
- पहले अरब (billion) अंकों वाले Mersenne Prime की खोज जो केवल 10^{9} (या अधिक) अंकों के साथ Mersenne Prime है।आपको एक मिलियन डॉलर का अच्छा लाभ देगा लेकिन तभी जब आप इसे सत्यापित करेंगे।एक बोधगम्य परीक्षण हालांकि यह आपको लगभग 6×10^{8} अंक ($150000 का एक पुरस्कार) प्राप्त करेगा।यह परीक्षा करना होगा कि क्या \left(2^{2,147,483,647}-1\right) एक मेर्सन प्राइम है?
- प्रसिद्ध गणितज्ञ लियोनहार्ड यूलर (Leonhard Euler) ने मेर्सन प्राइम 2^{31}-1 की खोज की जो कि एक परिपूर्ण संख्या से मेल खाती है।1772 में यूलर द्वारा खोजा गया यह 90 से अधिक वर्षों तक सबसे बड़ा ज्ञात प्राइम नंबर बना रहा।यह अप्रमाणित अनुमान है कि \left(2^{2,147,483,647}-1\right) एक मेर्सन प्राइम भी है।
कई उम्मीदवार Mersenne Prime के बारे में यह कहकर नीचे गिरा दिया कि उन्हें आमतौर प्राईमस (Primes) में विभाजित किया जा सकता है।जैसे 2047=23×89।1903 में पहले ही ज्ञात था कि 2^{67}-1 मेर्सन प्राइम नहीं था लेकिन कोई नहीं जानता था कि इसके गुणनखंड क्या है? फ्रैंक नेलसन रोल (Frank Nelson Cole) ने अमेरिकन मैथमेटिकल सोसायटी को “ऑन द फैक्टोराइजेशन ऑफ लार्ज नंबर्स (on the Factorization of Large Numbers)” शीर्षक से एक वार्ता दी।बोर्ड के बाई ओर उन्होंने गणना \left(2^{67}-1\right) की जिसे 147,573,952,589,676,412,927 लिखा और दाईं ओर उन्होंने 193,707,721 × 761,838,257,287 लिखा।अपने घंटे के व्याख्यान को बिना कुछ कहे और इसे पूरा करने में बिताया।अंत में जब उन्होंने दिखाया कि दोनों पक्ष समान है तो वह खड़े होकर तालियां बजाते हुए बैठ गए।
- अब तक का सबसे बड़ा Mersenne Prime Number जो गुणन योग्य साबित हुआ वह है \left(2^{1,168,183}-1\right) जिसे (हाल ही फरवरी 2014 में) 54,763,676,838,381,762,583 (जो अभाज्य है) और 351,639 अंको (Digit) की संख्या में विभाजित होने के लिए दिखाया गया था,जिसे प्राइम भी माना जाता है।
- यह साबित हो चुका है कि मौजूद सभी सम पूर्ण संख्याएँ जो मेर्सन प्राइम द्वारा उत्पन्न होती है जो 2^{n} -1 का अनुसरण करती हैं और यह अनुमान लगाया जाता है (लेकिन अभी सिद्ध नहीं हुआ है) कि कोई विषम परिपूर्ण संख्या नहीं है।विषम परिपूर्ण संख्या का पता लगाना सदी की सबसे बड़ी गणितीय उपलब्धियों में से एक होगा।इस प्रकार 6/28 या 28/6 अर्थात् 28 जून आदर्श संख्या दिवस मनाने के रूप में आनंददायक है।
- उपर्युक्त आर्टिकल में 28 जून को परिपूर्ण संख्या दिवस (Perfect Number Day on 28th June),28 जून को परिपूर्ण संख्या दिवस का गणित अवकाश मनाएं (Celebrate The Mathematics Holiday Of Perfect Number Day on 28th June) के बारे में बताया गया है।
- आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:Pi Day
2.वफादार स्टूडेंट (हास्य-व्यंग्य) (Loyal Student) (Humour-Satire):
- गणित अध्यापक:(अपने मित्र से) यह मेरा वफादार स्टूडेंट है।स्कूल की सारी खबरें मुझे आकर बता देता है।
मित्र:(गणित अध्यापक से) इसमें वफादारी की क्या बात है? - गणित अध्यापक:(मित्र से) यह स्कूल में मेरे खिलाफ जो अध्यापक backbiting (निंदा करना, चुगलखोरी) करते हैं।मेरी आलोचना करते हैं तथा स्कूल से हटाने का षड़यन्त्र रच रहे होते हैं, वे सभी खबरे मुझे आकर बता देता है। तुम तो जानते हो कि गणित अध्यापक से अन्य अध्यापक कितने चिढ़ते हैं।
Also Read This Article:World Mathematics Day
3.28 जून को परिपूर्ण संख्या दिवस (Perfect Number Day on 28th June),28 जून को परिपूर्ण संख्या दिवस का गणित अवकाश मनाएं (Celebrate The Mathematics Holiday Of Perfect Number Day on 28th June) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्नः
प्रश्नः1.28 एक परिपूर्ण संख्या क्यों है? (Why is 28 a perfect number?):
उत्तर:हम किसी संख्या को परिपूर्ण के रूप में भी परिभाषित कर सकते हैं,जब उसके सभी भाजक, उचित और अनुचित का योग,संख्या से दोगुना हो। हम देखते हैं कि 28 अभी भी इस परिभाषा से परिपूर्ण है: इसके उचित भाजक 1, 2, 4, 7 और 14 हैं,इसका अनुचित भाजक 28 है और इसके सभी भाजक का योग, 1 + 2 + 4 + 7 + 14 + 28, 56 है, जो 2 × 28 है।
प्रश्न:2.24 एक परिपूर्ण संख्या क्यों है? (Why is 24 a perfect number?):
उत्तर:24 भी एकमात्र सम परिपूर्ण संख्या है जो पूर्णांकों के दो धनात्मक घनों का योग है।एक पूर्ण संख्या (चाहे सम या विषम) के भाजक की संख्या सम होनी चाहिए,क्योंकि N एक पूर्ण वर्ग नहीं हो सकता।इन दो परिणामों से यह पता चलता है कि प्रत्येक पूर्ण संख्या एक अयस्क की हार्मोनिक (Ore’s harmonic number) संख्या है।
(नोट:हमारी समझ नहीं आया कि गूगल सर्च इंजन में इसे परिपूर्ण संख्या क्यों बताया गया है।)
प्रश्न:3.साल का परिपूर्ण दिन कौन सा है? (What’s the perfect day of the year?):
उत्तर:जून 28
चाहे आप पहले महीना लिखें या तारीख, जो 28 जून को साल का एकमात्र “परिपूर्ण ” दिन बनाता है,एक गणितीय तथ्य जिसका आप आनंद ले सकते हैं -और, यदि आप चाहें, तो एक्सप्लोर करें – जब भी आप चाहें!
प्रश्न:4.कैलेंडर पर परिपूर्ण तारीख क्या है? (What is the perfect date on the calendar?):
उत्तर:संख्यात्मक रूप से परिपूर्ण तिथि खोज रहे हैं?आज ही साल का एकमात्र दिन है,जहां दोनों महीने (6) और तारीख (28) अलग-अलग परिपूर्ण संख्याएं हैं।6 जून पश्चिमी कैलेंडर पर एकमात्र अन्य परिपूर्ण संख्या तिथि है।
इस 28 जून को ‘परफेक्ट नंबर डे’ का गणित अवकाश मनाएं।
- उपर्युक्त प्रश्नों के उत्तर द्वारा 28 जून को परिपूर्ण संख्या दिवस (Perfect Number Day on 28th June),28 जून को परिपूर्ण संख्या दिवस का गणित अवकाश मनाएं (Celebrate The Mathematics Holiday Of Perfect Number Day on 28th June) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
Perfect Number Day on 28th June
28 जून को परिपूर्ण संख्या दिवस
(Perfect Number Day on 28th June)
Perfect Number Day on 28th June
28 जून को परिपूर्ण संख्या दिवस (Perfect Number Day on 28th June) प्रतिवर्ष समस्त
विश्व में मनाया जाता है।आइए जानते हैं परिपूर्ण संख्या तथा परिपूर्ण दिवस क्या है? परिपूर्णता एक अप्राप्य खोज है
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |