Parallel Lines and Transversal Lines
1.समान्तर रेखाएँ और तिर्यक रेखा (Parallel Lines and Transversal Lines),समान्तर रेखाएँ और तिर्यक रेखा कक्षा 9 (Parallel Lines and Transversal Lines Class 9):
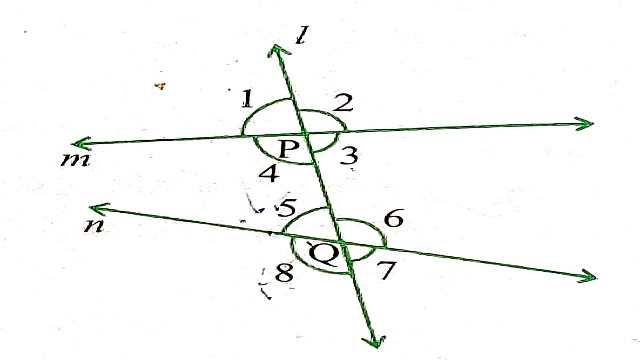
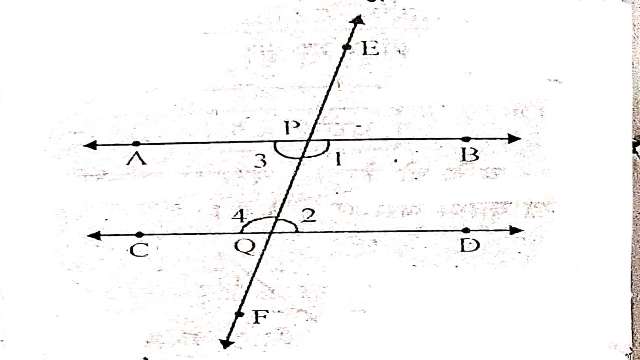
समान्तर रेखाएँ और तिर्यक रेखा (Parallel Lines and Transversal Lines) में तिर्यक रेखा वह रेखा है जो दो या अधिक रेखाओं को भिन्न बिन्दुओं पर प्रतिच्छेद करती है।(देखिए आकृति) रेखा l रेखाओं m और n को क्रमशः बिन्दुओं P और Q पर प्रतिच्छेद करती है।अतः रेखा l रेखाओं m और n के लिए एक तिर्यक रेखा है।
\angle 1,\angle 2, \angle 7 \text { और } \angle 8 बाह्य कोण (exterior angles) कहलाते हैं। \angle 3,\angle 4, \angle 5 \text { और } \angle 6 अन्तःकोण (interior angles) कहलाते हैं।
(a)संगत कोण (corresponding angles)
(i) \angle 1 और \angle 5
(ii)\angle 2 और \angle 6
(iii)\angle 4 और \angle 8
(iv) \angle 3 और \angle 7
(b)एकान्तर अन्तःकोण (Alternate interior angles)
(i) \angle 4 और\angle 6
(ii)\angle 3 और \angle 5
(c) एकान्तर बाह्य कोण (Alternate exterior angles)
(i)\angle 1 और \angle 7
(ii) \angle 2 और \angle 8
(d) तिर्यक रेखा के एक ही ओर के अन्तःकोण
(i) \angle 4 और \angle 5
(ii) \angle 3 और \angle 6
तिर्यक रेखा के एक ही ओर अन्तःकोणों को क्रमागत अन्तःकोण (Consecutive Interior Angles) या सम्बन्धित कोण (Allied Angles) या सह-अन्तःकोण (Co-interior Angles) भी कहा जाता है।साथ ही,अनेक बार हम एकान्तर अन्तःकोणों के लिए केवल शब्दों एकान्तर कोणों का प्रयोग करते हैं।
अभिगृहीत:6.3.यदि एक तिर्यक रेखा दो समान्तर रेखाओं को प्रतिच्छेद करे,तो संगत कोणों का प्रत्येक युग्म बराबर होता है।
जब रेखाएँ m और n समान्तर हैं
अतः \angle 1=\angle 5, \angle 2=\angle 6, \angle 4=\angle 8 और \angle 3=\angle 7
संगत कोण अभिगृहीत का विलोम (Converse of Corresponding Angles Axioms)
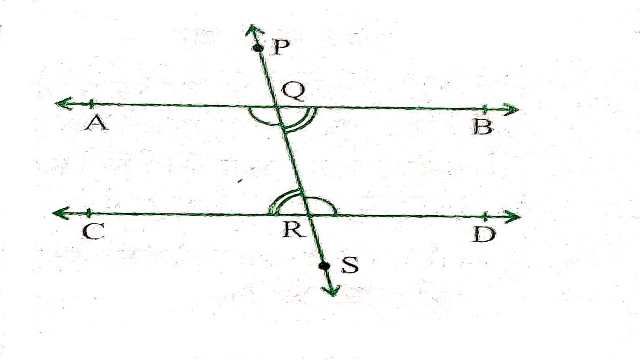
एक रेखा AD खींचिए और उस पर दो बिन्दु B और C अंकित कीजिए।B और C पर क्रमशः \angle ABQ और \angle BCS की रचना कीजिए जो परस्पर बराबर हों जैसा कि आकृति (i) में दर्शाया गया है।
QB और SC को AD के दूसरी ओर बढ़ाकर रेखाएँ PQ और RS प्राप्त कीजिए जैसा कि आकृति (ii) में दर्शाया गया है।ये रेखाएँ परस्पर प्रतिच्छेद नहीं करती।आप दोनों रेखाओं PQ और RS के विभिन्न बिन्दुओं पर उभयनिष्ठ लम्ब खींचकर और उनकी लम्बाईयाँ मापकर देख सकते हैं कि ये लम्बाईयाँ प्रत्येक स्थान पर बराबर हैं।अतः निष्कर्ष निकाल सकते हैं कि ये रेखाएँ समान्तर हैं।अर्थात् संगत कोण अभिगृहीत का विलोम भी सत्य है।
अभिगृहीत:6.4.यदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार प्रतिच्छेद करे कि संगत कोणों का एक युग्म बराबर है,तो दोनों रेखाएँ परस्पर समान्तर होती हैं।
प्रमेय (Theorem):6.2.यदि एक तिर्यक रेखा दो समान्तर रेखाओं को प्रतिच्छेद करे तो एकान्तर अन्तःकोणों का प्रत्येक युग्म बराबर होता है।
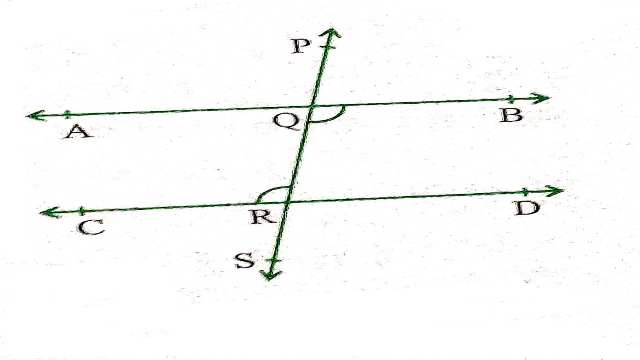
आकृति में तिर्यक रेखा PS समान्तर रेखाओं AB और CD को क्रमशः बिन्दुओं Q और R पर प्रतिच्छेद करती है।
\angle BQR=\angle QRC और \angle AQR=\angle QRD (एकान्तर कोण)
\angle PQA=\angle QRC (संगत कोण अभिगृहीत से)
(1) व (2) से
\angle PQA=\angle BQR \ldots(2)
(1) व (2) से हम निष्कर्ष निकाल सकते हैं कि
\angle BQR=\angle QRC
इसी प्रकार \angle AQR=\angle QRD
प्रमेय (Theorem):6.3.यदि एक तिर्यक रेखा दो रेखाओं को इस प्रकार प्रतिच्छेद करे कि एकान्तर अन्तःकोणों का एक युग्म बराबर है तो दोनों रेखाएँ परस्पर समान्तर होती हैं।
आकृति में तिर्यक रेखा PS रेखाओं AB और CD को क्रमशः Q और R पर इस प्रकार प्रतिच्छेद करती है कि \angle BQR=\angle QRC है।
\angle BQR=\angle PQA (शीर्षाभिमुख कोण)……(1)
\angle BQR=\angle QRC (दिया है)………(2)
अतः (1) और (2) से हम निष्कर्ष निकाल सकते हैं कि
परन्तु ये संगत कोण हैं।
अतः है। (संगत कोण अभिगृहीत का विलोम)
प्रमेय (Theorem):6.4.यदि एक तिर्यक रेखा दो समान्तर रेखाओं को प्रतिच्छेद करे तो तिर्यक रेखा के एक ही ओर के अन्तःकोणों का प्रत्येक युग्म संपूरक होता है।
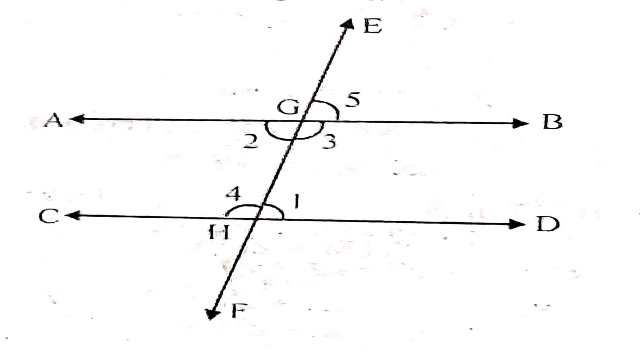
दिया है (Given):दो समान्तर रेखाओं AB और CD को तिर्यक रेखा EF क्रमशः G और H पर प्रतिच्छेद करती है।
सिद्ध करना है (To Prove):(i) \angle 1=\angle 2 और \angle 3=\angle 4
(ii) \angle 1+\angle 3=180^{\circ} और \angle 2+\angle 4=180^{\circ}
उपपत्ति (Proof): \angle 3+\angle 5=180^{\circ}(रैखिक कोण युग्म)
परन्तु \angle 5=\angle 1 (संगत कोण)
\therefore \angle 1+\angle 3=180^{\circ}
तथा \angle 1+\angle 4=180^{\circ} (रैखिक कोण युग्म)
परन्तु \angle 1=\angle 2 (एकान्तर कोण)
\angle 2+\angle 4=180^{\circ}
अतः \angle 1+\angle 3=180^{\circ} और \angle 2+\angle 4=180^{\circ}
प्रमेय (Theorem):6.5.यदि एक तिर्यक रेखा दो समान्तर रेखाओं को प्रतिच्छेद करे, तो तिर्यक रेखा के एक ही ओर के अन्तःकोणों का प्रत्येक युग्म संपूरक होता है।
दिया है (Given):एक तिर्यक रेखा EF दो समान्तर रेखाओं AB तथा CD को P और Q पर प्रतिच्छेद करती है।
\angle 1+\angle 2=180^{\circ}
सिद्ध करना है (To Prove): AB \| CD
उपपत्ति (Proof): \angle 1+\angle 3=180^{\circ} (रैखिक कोण युग्म)
\angle 1+\angle 2=180^{\circ} (दिया है)
परन्तु ये एकान्तर कोण हैं।
\therefore \angle 1+\angle 3=\angle 1+\angle 2 \\ \angle 3=\angle 2
अतः AB \| CD
प्रमेय (Theorem):6.6.वे रेखाएँ जो एक ही रेखा के समान्तर हों, परस्पर समान्तर होती हैं।
दिया है (Given):तीन रेखाएँ AB,CD और EF इस प्रकार हैं कि AB \| CD तथा CD \| EF
सिद्ध करना है (To Prove): AB \| EF
रचना (Construction):एक तिर्यक रेखा खींची जो AB,CD और EF को P,Q और R पर प्रतिच्छेद करे।
उपपत्ति (Proof): \angle 1=\angle 2 (संगत कोण)
\angle 2 =\angle 3 (संगत कोण)
\therefore \angle 1 =\angle 3
परन्तु यह संगत कोणों का एक युग्म है
अतः AB \| EF
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Lines and Angles Class 9
2.समान्तर रेखाएँ और तिर्यक रेखा के साधित उदाहरण (Parallel Lines and Transversal Lines Solved Examples):
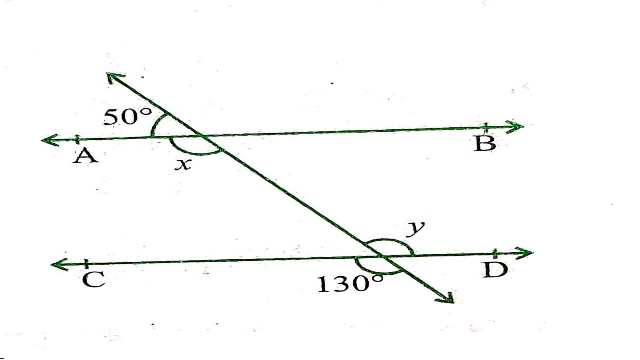
Example:1.आकृति में x और y के मान ज्ञात कीजिए और फिर दर्शाइए कि है।
Solution:x+50°=180° (रैखिक कोण युग्म)
x=180°-50°=130°
y=130° (शीर्षाभिमुख कोण)
अब x=y
परन्तु ये एकान्तर कोण हैं।
अतः AB || CD
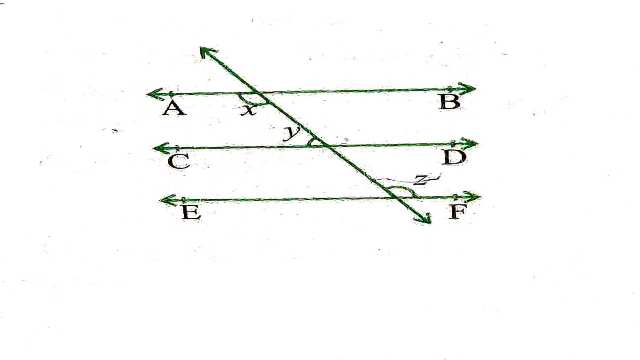
Example:2.आकृति में यदि AB || CD , CD || EF और y:z=3:7 है, तो x का मान ज्ञात कीजिए।
Solution:AB || CD
x+y=180° (तिर्यक रेखा के एक ही ओर के अन्तः कोणों का योग)
AB || CD और CD || EF
AB || EF
\therefore x=z (एकान्तर कोण)
\therefore z+y=180°
अब y:z=3:7
\Rightarrow \frac{y}{z}=\frac{3}{7} \Rightarrow y=\frac{3 z}{7} \\ \therefore z+\frac{3}{7} z=180^{\circ} \\ \Rightarrow 7 z+3 z=180^{\circ} \times 7 \\ \Rightarrow 10z=180^{\circ} \times 7 \\ \Rightarrow z=126^{\circ}
x=z
x=126°
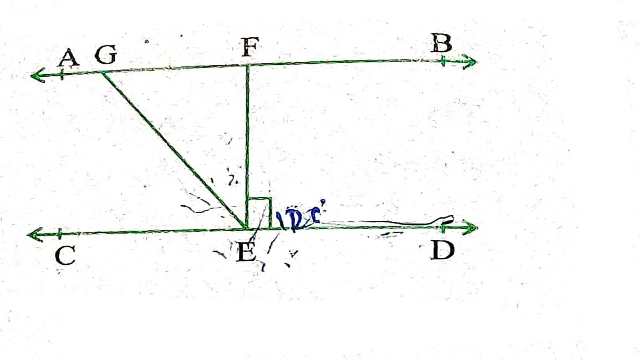
Example:3.आकृति में यदि AB || CD, EF ⊥ CD और \angle GED=126^{\circ} है तो \angle AGE, \angle GEF और \angle FGE ज्ञात कीजिए।
Solution: \angle DEF=90^{\circ} (दिया है)
और \angle GED=126^{\circ} \\ \therefore \angle D E F+\angle G E F=126^{\circ} \\ 90^{\circ} +\angle G E F=126^{\circ} \\ \Rightarrow \angle G E F=126^{\circ}-90^{\circ}=36^{\circ} \\ \angle AGE=\angle G E F+\angle EFG (बाह्य कोण प्रमेय से)
परन्तु \angle E F G=\angle FED (एकान्तर कोण)
परन्तु \angle F E D=90^{\circ} \\ \therefore \angle E F G=90^{\circ} \\ \therefore \angle AGE=36^{\circ}+90^{\circ}=126^{\circ}
और \angle A G E+\angle E G F=180^{\circ} (रैखिक कोण युग्म)
अतः \angle 126^{\circ}+\angle E G F=180^{\circ} \\ \Rightarrow \angle EGF=180^{\circ} -126^{\circ}=54^{\circ} \\ \angle AGE=126^{\circ} \\ \angle GEF=36^{\circ} और \angle FGE=54^{\circ}
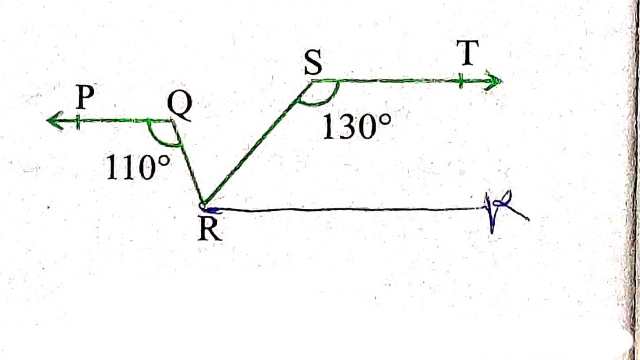
Example:4.आकृति में यदि PQ || ST, \angle PQR=110^{\circ} और \angle RST=130^{\circ} है तो \angle QRS ज्ञात कीजिए।
Solution:दिया है (Given): PQ || ST, \angle PQR=110^{\circ}, \angle RST=130^{\circ}
ज्ञात करना हैः \angle QRS
रचना (Construction): RK || ST
हल:- ST || RK \\ \therefore \angle TSR+\angle KRS=180^{\circ} (तिर्यक रेखा के एक ही ओर बने कोण)
परन्तु \angle TSR=130^{\circ} \\ \therefore 130^{\circ}+\angle K R S=180^{\circ} \\ \angle KRS=180^{\circ}-130^{\circ}=50^{\circ}
पुनः PQ || RK जैसे PQ || ST
\therefore \angle PQR=\angle Q R K \\ 110^{\circ}=\angle Q R S+\angle S R K \\ 110^{\circ}= \angle Q R S+50^{\circ} \\ \therefore \angle Q R S=110^{\circ}-50^{\circ} \Rightarrow \angle QRS=60^{\circ}
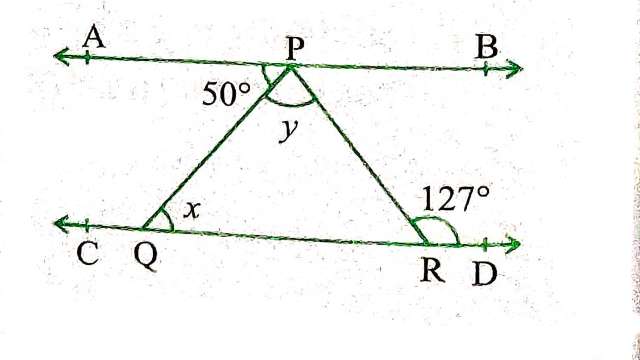
Example:5.आकृति में, यदि AB || CD, \angle APQ=50° और \angle PRD=127° है तो x और y ज्ञात कीजिए।
Solution: AB || CD
x=50° (एकान्तर कोण)
और x+y=127° (बाह्य कोण प्रमेय से)
50°+y=127°
y=127°-50°=77°
अतः x=50°,y=77°
Example:6.आकृति में, PQ और RS दो दर्पण हैं।एक आपतन किरण (incident-rays) पथ BC पर चलकर दर्पण RS से C पर टकराती है तथा पुनः CD के अनुदिश परावर्तित हो जाती है।सिद्ध कीजिए कि AB || CD
दिया है (Given): PQ || RS और AB दर्पण PQ को B पर आपतित है और परावर्तित किरण BC की दिशा में चलकर दर्पण RS को C पर टकराकर पुनः CD की दिशा में वापस मुड़ती है।
सिद्ध करना है (To Prove): AB || CD
रचना (Construction):दो दर्पणों पर B और C पर लम्ब खींचे।
उपपत्ति (Proof):AB एक आपतित किरण तथा BC एक परावर्तित किरण है।
\therefore \angle 1=\angle 2 \ldots(1)
चूँकि BC एक आपतित किरण और CD एक परावर्तित किरण है।
BM ⊥ PQ
और CL ⊥ RS (रचना से)
और PQ || RS (दिया है)
PQ || RS और BC इन्हें काटती है।
\therefore \angle 2=\angle 3 (एकान्तर कोण)
(1),(2) और (3) से हमें प्राप्त होता है कि
\therefore \angle 1=\angle 4 \ldots(4)
(3) और (4) को जोड़ने परः
\angle 1+\angle 2=\angle 3+\angle 4 \\ \Rightarrow \angle ABC=\angle BCD
परन्तु यह एकान्तर कोणों का एक युग्म है।
अतः CA || BC
उपर्युक्त उदाहरणों के द्वारा समान्तर रेखाएँ और तिर्यक रेखा (Parallel Lines and Transversal Lines),समान्तर रेखाएँ और तिर्यक रेखा कक्षा 9 (Parallel Lines and Transversal Lines Class 9) को समझ सकते हैं।
3.समान्तर रेखाएँ और तिर्यक रेखा पर आधारित सवाल (Questions Based on Parallel Lines and Transversal Lines):
(1.)एक त्रिभुज का एक बाह्य कोण 115° है और एक सम्मुख कोण 35° है।त्रिभुज के अन्य दो कोणों के माप ज्ञात करो।
(2.)त्रिभुज DEF की भुजाओं EF,FD और DE को क्रमानुसार बढ़ाकर तीन बहिष्कोण क्रमशः DEP,EDQ और FER बनाये गये हैं।
सिद्ध कीजिए किः \angle DFP+\angle EDQ+\angle FER=360°
उपर्युक्त सवालों को हल करने पर समान्तर रेखाएँ और तिर्यक रेखा (Parallel Lines and Transversal Lines),समान्तर रेखाएँ और तिर्यक रेखा कक्षा 9 (Parallel Lines and Transversal Lines Class 9) को ठीक से समझ सकते हैं।
Also Read This Article:-Versions to Euclid 5th Postulate
4.समान्तर रेखाएँ और तिर्यक रेखा (Frequently Asked Questions Related to Parallel Lines and Transversal Lines),समान्तर रेखाएँ और तिर्यक रेखा कक्षा 9 (Parallel Lines and Transversal Lines Class 9) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्नः
प्रश्नः1.संगत कोण युग्मों में क्या सम्बन्ध होता है जब दो या अधिक समान्तर रेखाओं को एक तिर्यक रेखा प्रतिच्छेद करे? (What is the Relation Between the Corresponding Angles Pairs When Two or More Parallel Lines Intersect by a Transversal Line?):
उत्तरःदो या अधिक समान्तर रेखाओं को एक तिर्यक रेखा प्रतिच्छेद करे तो
(1.)संगत कोण बराबर होते हैं।
(2.)एकान्तर कोण बराबर होते हैं।
(3.)अन्तःकोण सम्पूरक होते हैं।
उपर्युक्त कथनों का विलोम भी सत्य होते हैं अर्थात् दो सरल रेखाओं को एक तिर्यक रेखा प्रतिच्छेद करे और संगत कोण बराबर हों तो वे रेखाएँ समान्तर होती हैं।
प्रश्न:2.शीर्षाभिमुख कोण किसे कहते हैं? (What is Vertically Opposite Angles?):
उत्तरःयदि दो रेखाएँ एक-दूसरे को प्रतिच्छेद करे,तो प्रतिच्छेद बिन्दु पर एक-दूसरे से विपरीत बने कोण शीर्षाभिमुख कोण कहलाते हैं।
प्रश्न:3.रैखिक कोण युग्म किसे कहते हैं? (What is a Linear Pair of Angles?):
उत्तरःदो आसन्न कोणों को जिनकी उभयनिष्ठ भुजा के अतिरिक्त भुजाएँ दो विपरीत किरणें हों।कोणों की बाह्य भुजाएँ दो विपरीत किरणे हैं अर्थात् वे एक रेखा में हों तो कोणों का मापों का योगफल 180° के बराबर होता है।
उपर्युक्त प्रश्नों के उत्तर द्वारा समान्तर रेखाएँ और तिर्यक रेखा (Parallel Lines and Transversal Lines),समान्तर रेखाएँ और तिर्यक रेखा कक्षा 9 (Parallel Lines and Transversal Lines Class 9) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Parallel Lines and Transversal Lines
समान्तर रेखाएँ और तिर्यक रेखा
(Parallel Lines and Transversal Lines)
Parallel Lines and Transversal Lines
समान्तर रेखाएँ और तिर्यक रेखा (Parallel Lines and Transversal Lines) में तिर्यक रेखा वह
रेखा है जो दो या अधिक रेखाओं को भिन्न बिन्दुओं पर प्रतिच्छेद करती है।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.