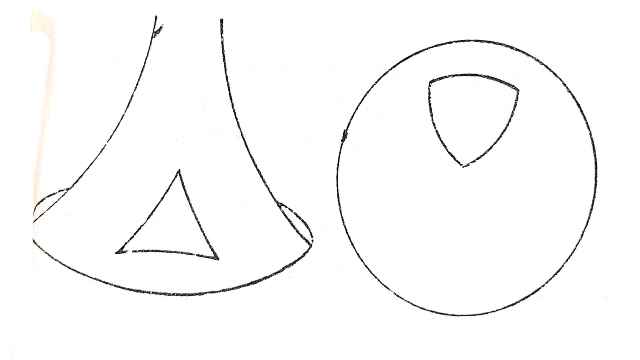Non Euclidean Geometry
1.अ-यूक्लिडीय ज्यामितियाँ (Non Euclidean Geometry):
- अ-यूक्लिडीय ज्यामितियाँ (Non Euclidean Geometry)!यूक्लिड के विरोध में निर्मित ज्यामितियाँ!एक नहीं अनेक!किन्तु यूक्लिड का विरोध कैसा?यह जानने के लिए हमें पुनः यूक्लिड की ज्यामिति की ओर लौटना होगा;यूक्लिड की ज्यामिति का गहराई से परीक्षण करना होगा।यूक्लिड की ज्यामिति का आरम्भ आधारशिलाओं-परिभाषाओं,अभिधारणाओं तथा स्वयंतथ्यों से होता है।ज्यामिति की ये आधारशिलाएं ही मजबूत नहीं होगी तो देर-सबेर ज्यामिति का भवन अवश्य ही ढह जाएगा।
- हम यह तो नहीं कहेंगे कि यूक्लिड की ज्यामिति का भवन ढह गया है।परंतु इतना तो अवश्य कहा जा सकता है कि यह भवन जर्जर हो गया है।इसका मुख्य कारण यह है कि यूक्लिड की ज्यामिति की आधारशिलाएँ मजबूत नहीं थी।
कभी भी न मिलने वाली रेखाएं समांतर रेखाएं कहलाती है।सैद्धांतिक रूप से केवल इतना स्वीकार कर लिया जाता है कि दो समांतर रेखाएं ‘अनंत दूरी’ पर जाकर ही मिलती हैं।रेलगाड़ी की दो पटरियाँ समांतर रेखाओं का एक अच्छा उदाहरण है।
- यूक्लिड के समय से ही इस अभिधारणा की सत्यता के बारे में गणितज्ञों को संदेह होने लगा था।प्रसिद्ध ज्योतिषी तोलेमी ने भी इस अभिधारणा को सिद्ध करने का प्रयत्न किया था।तब से शताब्दियों तक चोटी के लगभग सभी गणितज्ञ इस अभिधारणा से उलझते रहे किंतु किसी को भी पहली चार अभिधारणाओं से या अन्य किसी सरल अभिधारणा के आधार पर इस पांचवी अभिधारणा को सिद्ध करने में सफलता नहीं मिली।
- सचमुच ऊपरी निगाह से देखें तो इस पांचवी अभिधारणा का कथन स्वयंसत्य जान पड़ता है।बिंदु प से रेखा अब के समांतर केवल एक ही रेखा खींची जा सकती है।यदि बिंदु प से दो या अधिक रेखाएं खींची जाए तो वे रेखाएं अब के समांतर नहीं रहेंगी और अंततोगत्वा रेखा अब से जाकर टकराएँगी।
- लेकिन गणित शास्त्र ‘दृष्टि-सत्य’ को परम-सत्य नहीं मानता।हमारी दृष्टि धोखा दे सकती है।इसलिए इस अवधारणा को हमें तर्क की कसौटी पर कसना ही होगा।
- यूक्लिड ने ग्रंथ के आरंभ में परिभाषाओं के बाद पांच अभिधारणाएं दी है।इन अभिधारणाओं के पहले ही उसने स्पष्ट लिख दिया है कि यदि हम यह स्वीकार कर लें …..।
- अर्थात् यूक्लिड की ज्यामिति के लिए हमें इन अभिधारणाओं को बिना संदेह के स्वीकार कर लेना है।इनकी सत्यता के लिए किसी प्रमाण की जरूरत नहीं है,ये स्वयंसिद्ध है।परंतु यूक्लिड की पांचवी अभिधारणा के बारे में यह बात नहीं कही जा सकती।स्वयं यूक्लिड को भी अपनी पांचवी अभिधारणा के बारे में शायद संदेह था।यूक्लिड के बाद तो प्राय: प्रत्येक गणितज्ञ ने इस अभिधारणा को सिद्ध करने की कोशिश की है किंतु किसी को भी इसमें सफलता नहीं मिली!
- यूक्लिड की पांचवी अभिधारणा है:
- अब एक सीधी रेखा है और इस रेखा के बाहर एक निर्दिष्ट बिंदु है।तब प बिंदु से अब रेखा के समांतर एक और केवल एक ही सीधी रेखा खींची जा सकती है।
- चूँकि इस अभिधारणा में ‘समांतर'(पैरेलल) शब्द महत्त्व का है,इसलिए इस धारणा को समान्तरण की अभिधारणा का नाम दिया गया है।किसी धारणा को सिद्ध करने का एक तरीका यह भी है कि इसे गलत मान लिया जाए और तब देखा जाए कि क्या परिणाम निकलता है।यदि परिणाम प्रतिकूल निकलता है तो मान्य धारणा गलत सिद्ध होती है।
- यूक्लिड की यह समांतर की अभिधारणा दो प्रकार से असत्य हो सकती है।(1)एक से अधिक समांतर रेखाएं हो सकती हैं;या (2)एक भी समांतर रेखा नहीं हो सकती।ये दोनों परिकल्पनाएँ 5वीं अभिधारणा को असत्य ठहराती हैं।
गणितज्ञों का ध्यान सबसे पहले दो समांतरों पर गया।गणितज्ञ साच्छेरी (1667-1733) ने दो समांतर रेखाओं की कल्पना करके प्रतिकूल परिणामों पर पहुंचने की कोशिश की।यदि वह प्रतिकूल परिणामों पर पहुंचते तो एक समांतर रेखा वाली अभिधारणा को सही मान लेते।परंतु जब वह किसी प्रतिकूल परिणाम पर नहीं पहुंचे तो उन्होंने समझ लिया कि उनका प्रयास असफल रहा। - असल में साच्छेरी ने एक नई ज्यामिति अ-यूक्लिडीय की नींव रख दी थी।
हंगेरी के एक तरुण गणितज्ञ योनोस बोल्याई (1802-1860 ई.) ने यूक्लिड की इस समान्तरण अभिधारणा को ही अस्वीकार किया।उनके मतानुसार ज्यामिति की रचना के लिए इस अभिधारणा की आवश्यकता ही नहीं है।उन्होंने एक नई अभिधारणा के आधार पर एक नई ज्यामिति का निर्माण किया।
- बोल्याई की इस नई अभिधारणा के अनुसार एक बिंदु में से अन्य किसी रेखा के समांतर एक से अधिक समांतर रेखाएं खींची जा सकती है।
- लगभग उसी समय रूसी गणितज्ञ लोबाचेवस्की (1793-1856 ई.) की तरह स्वतंत्र रूप से एक नई ज्यामिति का निर्माण किया।लोबाचेवस्की की भी यही मान्यता थी कि एक बिंदु में से अन्य किसी रेखा के समांतर अनेक रेखाएं खींची जा सकती हैं।ऊपर की आकृति बोल्याई तथा लोबाचेवस्की की अभिधारणा के अनुरूप है।इन गणितज्ञों की अभिधारणा के अनुसार बिंदु प से खींची गई ये सारी रेखाएं अब रेखा के समांतर है।
- बोल्याई तथा लोबाचेवस्की की अभिधारणा पर एकाएक विश्वास नहीं होता।क्योंकि आंखें स्पष्ट देख रही हैं कि एक के अलावा बिंदु प से गुजरने वाली शेष सभी रेखाएं अब रेखा के समांतर नहीं है।ये अंततोगत्वा अब रेखा से मिलेंगी ही।
और अ-यूक्लिड की ज्यामिति के अध्ययन में सबसे बड़ी कठिनाई यही है।ज्यामितीय आकृतियों पर विश्वास नहीं रह जाता।परंतु तथ्य यही है कि लोबाचेवस्की और बोल्याई की इन नई अभिधारणाओं में कोई असंगति नहीं है।दरअसल प्रकृति में समतलों के अलावा ऐसे भी तलों का अस्तित्व है जिन पर एक बाह्य बिंदु से एक प्रदत्त रेखा के समांतर एक से अधिक रेखाएं खींची जा सकती हैं।
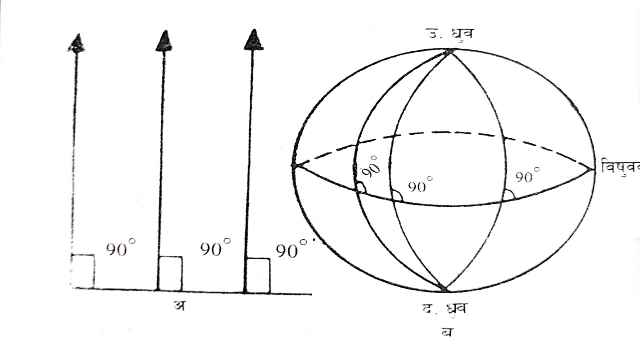
- महान् जर्मन गणितज्ञ रीमान् (1826-1866 ई.) ने तो एक नया ही मत व्यक्त किया।उनकी परिकल्पना के अनुसार किसी भी समांतर रेखा का अस्तित्व ही नहीं है।अपनी इसी परिकल्पना के आधार पर उन्होंने एक नई अ-यूक्लिडीय ज्यामिति की रचना कर डाली।रीमान् की इस ज्यामिति को एक गोल पर समझा जा सकता है।एक समतल पर हम कल्पना कर सकते हैं कि जो रेखाएं एक रेखा के साथ 90 डिग्री का कोण बनाती हैं,वे एक दूसरे के समांतर होती है,आकृति (अ)।अब हम इसी स्थिति को पृथ्वी की गोल सतह पर लागू करके देखते हैं,आकृति (ब)।सभी याम्योत्तर या देशांतर रेखाएं (मेरीडियन) विषवत रेखा के साथ 90 डिग्री का कोण बनाती है। फिर भी ये सभी याम्योत्तर उत्तर तथा दक्षिण ध्रुवों पर एक बिंदु में मिलते हैं।
- रीमानीय ज्यामिति में भी यही होता है।रीमानीय ज्यामिति के लिए गोल एक उचित सतह है।
अब प्रश्न उठता है:यूक्लिड की पांचवी अभिधारणा के स्थान पर ये नाना प्रकार की अवधारणाएं स्वीकार की जाएँ तो ज्यामिति के प्रमेयों का क्या हाल होगा? - यूक्लिड की पांचवी अभिधारणा के बिना भी उनकी ज्यामिति के अधिकांश प्रमेय सिद्ध किए जा सकते हैं।इसलिए इस अभिधारणा में बदल हो जाने पर भी यूक्लिड की ज्यामिति के बहुत से प्रमेय ज्यों-के-त्यों बने रहेंगे परंतु कुछ ऐसे भी हैं जो विभिन्न रूप धारण कर लेंगे।यूक्लिड की ज्यामिति के एक प्रसिद्ध प्रमेय का ही उदाहरण लेते हैं।यह प्रमेय है:
किसी भी त्रिभुज के तीनों अंतर्कोणों का योग 180 होता है। - परंतु जिन अ-यूक्लिडीय ज्यामितियों में अनेक समान्तरों की अभिधारणा को स्वीकार किया गया है,उनमें यह योग 180° से कम होगा।और जिन ज्यामितियों में किसी भी समांतर को स्वीकार नहीं किया गया है उनमें यह योग सदैव 180° से अधिक रहेगा।
- ऊपर की आकृतियों में दो भिन्न तलों पर दो त्रिभुज खींचे गए हैं।बाई ओर की आकृति में त्रिभुज के तीनों कोणों का योग 180° से कम है और दाईं ओर की आकृति में त्रिभुज के तीनों कोणों का योग 180° से अधिक है।यूक्लिडीय समतल पर त्रिभुज का आकार चाहे जो भी रहे त्रिभुज के कोणों का योग 180° ही रहेगा।परंतु ऊपर के चित्रों की सतहों पर त्रिभुज के बदलते आकारों के साथ त्रिभुजों के कोणों के योग में भी बदल होता रहेगा।
- यूक्लिड की ज्यामिति में ऐसे अनेक प्रमेय है जो उपर्युक्त प्रमेय (त्रिभुज के तीनों कोणों का योग 180° होता है) से सिद्ध होते हैं इसलिए इस प्रमेय की तरह वे प्रमेय भी अ-यूक्लिडीय ज्यामिति में बदल जाएंगे।
- जब तक केवल एक ही ज्यामिति यूक्लिड की ज्यामिति का अस्तित्व था तब तक यही मान लिया गया था कि यही ज्यामिति भौतिक जगत की असली ज्यामिति है,परंतु अब अनेक ज्यामितियाँ अस्तित्व में आने पर प्रश्न उठता है कि इनमें सही ज्यामिति कौन-सी है?इनमें कौन-सी ज्यामिति भौतिक जगत पर लागू होती है?
- बीसवीं शताब्दी के महान भौतिकवेत्ता अल्बर्ट आइंस्टाइन इस निर्णय पर पहुंचे कि अ-यूक्लिडीय ज्यामिति ही विश्व की असली ज्यामिति है।उन्होंने अपने आपेक्षिकता के सिद्धांत में अ-यूक्लिडीय ज्यामिति का ही इस्तेमाल किया है।उन्होंने यह भी कहा था कि चूंकि ब्रह्मांडीय आकाश की तुलना में हमारी पृथ्वी बहुत छोटी है इसलिए पृथ्वी की सतह पर यूक्लिडीय ज्यामिति ही उपयोगी है।परंतु अतिविशाल विश्व की सीमाओं का अध्ययन केवल अ-यूक्लिडीय ज्यामिति से ही संभव है।आइंस्टाइन ने ज्यामिति तथा गुरुत्वाकर्षण के बीच भी संबंध स्थापित किया है।
- आधुनिक वैज्ञानिक ज्यामितियों को दो भागों में बांटते हैं।गणितीय ज्यामिति और भौतिकी ज्यामिति।गणितीय दृष्टि से देखा जाए तो अनेक ज्यामितियों का अस्तित्व है और ये सभी अपने आप में तार्किक दृष्टि से सही है।विशुद्ध गणितज्ञ इस बात की परवाह नहीं करता कि उसकी अभिधारणाएं भौतिक जगत के अनुसार सही है या नहीं।वह केवल अपनी ‘योजना’ के भीतर यही देखता है कि उसकी अभिधारणाएँ तथा प्रमेयों के बीच किसी प्रकार की कोई तार्किक असंगति नहीं होनी चाहिए।यदि आभिधारणाएं सही हैं तो उन पर आधारित प्रमेय भी सही होनी चाहिए।
- जो भी हो विज्ञान तथा गणित के इतिहास में यूक्लिड का स्थान चिरस्थाई बना रहेगा।अपने सिद्धांत में अ-यूक्लिडीय ज्यामिति का उपयोग करनेवाले महान आइंस्टाइन ने यूक्लिड की प्रतिभा के बारे में कहा है:
- “उसने (यूनान ने) पहली बार एक तार्किक योजना के बौद्धिक चमत्कार को जन्म दिया है।इस चमत्कार के कथन एक-दूसरे से इतनी दृढ़ता से फलित होते हैं कि एक भी उपपत्ति पर यत्किंचित संदेह नहीं किया जा सकता है-ऐसी है यूक्लिड की ज्यामिति।
- इस आर्टिकल में अ-यूक्लिडीय ज्यामितियाँ (Non Euclidean Geometry) के बारे में बताया गया है।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:What are Some Strengths in Math?
2.अ-यूक्लिडीय ज्यामितियाँ (Non Euclidean Geometry) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.गैर-यूक्लिडियन ज्यामिति का क्या अर्थ है? (What is meant by non-Euclidean geometry?):
प्रश्न:2.गैर-यूक्लिडियन ज्यामिति का एक उदाहरण क्या है? (What is an example of non-Euclidean geometry?):
प्रश्न:3.यूक्लिडियन ज्यामिति बनाम गैर-यूक्लिडियन क्या है? (What is Euclidean geometry vs non-Euclidean?):
प्रश्न:4.गैर-यूक्लिडियन ज्यामिति के विभिन्न प्रकार क्या हैं? (What are the different types of non-Euclidean geometry?):
प्रश्न:5.ज्यामिति के 3 प्रकार क्या हैं? (What are the 3 types of geometry?):
Also Read This Article:Laboratory of Mathematics
उपर्युक्त प्रश्नों के उत्तर द्वारा अ-यूक्लिडीय ज्यामितियाँ (Non Euclidean Geometry) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
Non Euclidean Geometry
अ-यूक्लिडीय ज्यामितियाँ
(Non Euclidean Geometry)
Non Euclidean Geometry
अ-यूक्लिडीय ज्यामितियाँ (Non Euclidean Geometry)!यूक्लिड के विरोध में निर्मित ज्यामितियाँ!एक नहीं अनेक!
किन्तु यूक्लिड का विरोध कैसा?यह जानने के लिए हमें पुनः यूक्लिड की ज्यामिति की ओर लौटना होगा;
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |