1.एक चिकने ऊर्ध्वाधर वृत्त के बाहर की ओर गति (Motion Outside Soomth Vertical Circle),एक चिकने ऊर्ध्वाधर वृत्त या गोले के बाहर की ओर कण की गति (Motion of a Particle on Outside of a Smooth Vertical Circle or Sphere)-

एक चिकने ऊर्ध्वाधर वृत्त के बाहर की ओर गति (Motion Outside Soomth Vertical Circle),एक चिकने ऊर्ध्वाधर वृत्त या गोले के बाहर की ओर कण की गति (Motion of a Particle on Outside of a Smooth Vertical Circle or Sphere)-त्रिज्या a के एक चिकने स्थिर वृत्त (या गोले की सतह) के उच्चतम बिन्दु पर कोई कण विराम की अवस्था में है जो थोड़ा सा विस्थापित किए जाने पर नीचे की ओर सरकने लगता है।ज्ञात कीजिए कि वह वृत्त से कहां पर अलग हो जाएगा और सिद्ध कीजिए कि अलग हो जाने के बाद एक परवलय बनाएगा जिसका नाबिलम्ब \frac{16}{27} होगा और यह भी सिद्ध कीजिए कि वह उर्ध्वाधर व्यास से \frac{5(\sqrt{5}+4 \sqrt{2}) a}{27} दूरी पर जाकर वृत्त (या गोले) के निम्नत्तम बिन्दु से गुजरने वाले क्षैतिज से टकराएगा।
(A heavy particle slides down the circle or surface of a smooth fixed sphere of radius a,being slightly displaced from rest at the highest point.Find where it will leave the circle.Also show that it will thereafter describe a parabola of latus rectum \frac{16}{27} .Prove also that it will strike the horizontal plane through the lowest point of the circle or sphere at a \frac{5(\sqrt{5}+4 \sqrt{2}) a}{27} distance from the vertical diameter.)
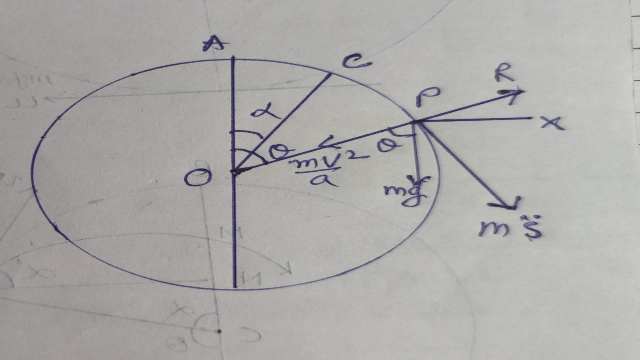
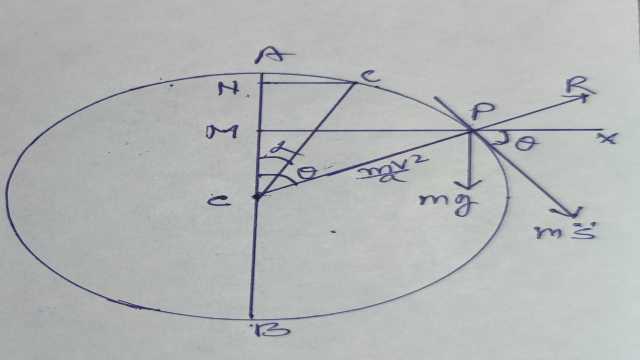
माना कि कण की संहति m है।इसे एक चिकने स्थिर गोले के पृष्ठ के उच्चत्तम बिन्दु पर रखकर विस्थापित किया जिससे वह गुरुत्वाकर्षण के अधीन फिसलने लग जाए।माना t समय पर कण बिन्दु P पर है तथा यदि वृत्त (या गोले) का केन्द्र O है तो त्रिज्या OP उर्ध्वाधर व्यास AB के साथ \theta कोण बनाती है।यह भी माना कि P पर कण का वेग v है तथा P पर वृत्त की प्रतिक्रिया R है।P से AB पर PN लम्ब डाला।

अब ऊर्जा समीकरण से हम जानते हैं कि
ऊर्जा का अन्तर=बलों द्वारा किया गया कार्य

\frac{1}{3} mv^{2}-\frac{1}{2} m u^{2}=mg(a-a \cos \theta) \\ \Rightarrow v^{2}=2 a g(1-\cos \theta)
अथवा
स्पर्श रेखा की ओर कण की गति का समीकरण होगा:

mv \frac{d v}{d s}=m g \sin \theta
[परन्तु वृत्त के लिए s=a \theta ]

\Rightarrow \frac{1}{2} v^{2}=-a g \cos \theta+c
प्रारम्भ में v=0 ,\theta=0 \\ \therefore 0=-a g+c
अतः v^{2}=2 a g(1-\cos \theta) \cdots(1)
तथा अभिलम्ब दिशा में कण की गति का समीकरण होगा:

\frac{m v^{2}}{a}=m r \cos \theta-R \\ \Rightarrow R=m[g \cos \theta-2 g(1-\cos \theta)] \\ \Rightarrow R=m g(3 \cos \theta-2) ...(2)
माना कि कण वृत्त P बिन्दु पर छोड़ देगा इसलिए P पर R=0

\therefore mg(3 \cos \theta-2)=0 \\ \Rightarrow \cos \theta=\frac{2}{3} चूंकि m g \neq 0
तथा P पर वेग v^{2} =2ga(1-\frac{2}{3}) \\ \Rightarrow v^{2} =\frac{2}{3} g a
जब कण वृत्त को छोड़ देगा तब वह गुरुत्वाकर्षण के अधीन गति करेगा तथा उसका गति पथ परवलय का अनुसरण करेगा।P को मूल बिन्दु लें तथा PX,PY क्षैतिज तथा उर्ध्वाधर रेखाओं को निर्देशांकाक्ष मानें तो कण के परवलय पथ का समीकरण होगा
\Rightarrow y=x \tan \alpha+\frac{1}{2} g \cdot \frac{x^{2}}{u^{2} \cos ^{2} \alpha} (कण की गति नीचे की ओर है)
यहां \alpha=a, u=v , \cos \theta=\frac{2}{3} तथा v^{2}(\frac{2ag}{3}) \\ y=\frac{\sqrt{5}}{2} x+\frac{27}{16 a} x^{2}...(3) \\ \text{परवलय का नाभिलम्ब=} \frac{2 \text {(P पर कण का क्षैतिज घटक)}^{2}}{g} \\ =\frac{2 v^{2} \cos ^{2} \theta}{g} \\ =2 \cdot\left(\frac{2 a g}{3}\right) \cdot\left(\frac{4}{g}\right) \cdot \frac{1}{g} \\ =\frac{16}{27} a
निम्नलिखित बिन्दु B से क्षैतिज BC का समीकरण होगा

y=NB=a+a \cos \theta=a+\frac{2 a}{3}=\frac{5 a}{3}....(4)
यदि कण BC को C पर मिलता है तो (3) तथा (4) को हल करने पर

\frac{5 a}{3}=\frac{\sqrt{5} x}{2}+\frac{27 x^{2}}{16a} \\ \Rightarrow x^{2}+\frac{8 \sqrt{5}}{27} a x-\frac{80}{81} a^{2}=0 \\ \Rightarrow x=-\frac{4 \sqrt{5}+20 \sqrt{2}}{27}=D C
BC= C की उर्ध्वाधर व्यास से दूरी

=BD+D C=P N+D C=a \sin \theta+x \\ =a\left[\frac{\sqrt{5}}{3}+\frac{-4 \sqrt{5}+20 \sqrt{2}}{27}\right] \\ =\frac{5(\sqrt{5}+4 \sqrt{2}) a}{27}
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:-Motion inside a smooth vertical circle

2.एक चिकने ऊर्ध्वाधर वृत्त के बाहर की ओर गति के उदाहरण (Motion Outside Soomth Vertical Circle Examples),एक चिकने ऊर्ध्वाधर वृत्त या गोले के बाहर की ओर कण की गति के उदाहरण (Motion of a Particle on Outside of a Smooth Vertical Circle or Sphere Examples)-

Example-1.एक कण को चिकने ऊर्ध्वाधर वृत्त के ऊपर रखा जाता है।यदि कण उस बिन्दु से चलना शुरू करे जिसकी वृत्त के सर्वोच्च बिन्दु से कोणीय दूरी हो तो सिद्ध करो कि जब \cos \theta=(\frac{2}{3}) \cos \alpha होगा तब कण वृत्त से सम्पर्क छोड़ देगा।
(A particle is placed on the outside of a smooth vertical circle.If the paricle starts from a point whose angular distance is from the highest point of the circle.Show that it will fly off when \cos \theta=(\frac{2}{3}) \cos \alpha.)
Solution-गति के समीकरण हैं-

m \frac{d^{2} s}{d t^{2}}=m g \sin \theta \cdots(1) \\ \frac{m v^{2}}{a}=m g \cos \theta-R \cdots (2) \\ v \frac{d v}{d s}=g \sin \theta \\ \Rightarrow v dv=g \sin \theta \frac{d s}{d \theta} \cdot d v \\ \Rightarrow v d v=ag \sin \theta d \theta
समाकलन करने पर-

v^{2}=-2 a g \cos \theta +A
जब \theta=\alpha , v^{2}=0 \quad \therefore A=2 a g \cos \alpha \\ \therefore v^{2}=2ag ( \cos \alpha-\cos \theta)
समीकरण (2) में v^{2} का मान रखने पर-

R =m g \cos \theta-m \frac{v^{2}}{a} \\ =m g \cos \theta-2 \operatorname{mg}(\cos \alpha-\cos \theta) \\ \Rightarrow R=m g(3 \cos \theta-2 \cos \alpha)
कण वृत्त से सम्पर्क छोड़ देगा जब R=0

\therefore m g \cos \theta-2 m g(\cos \alpha-\cos \theta)=0 \\ 3 \cos u=2 \cos \alpha \\ \Rightarrow \cos \theta=\frac{2}{3} \cos \alpha

Example-2.एक कण a त्रिज्या वाले स्थिर चिकने गोले के बाहरी तल के उच्चत्तम बिन्दु से \sqrt{\left(\frac{1}{2} a g\right)}  वेग से क्षैतिज दिशा में प्रक्षिप्त किया जाता है। सिद्ध करो कि वह गोले को ऐसे बिन्दु पर छोड़ेगा जिसकी प्रक्षेप बिन्दु से उर्ध्वाधर दूरी \frac{a}{6} है।
(A particle is projected horizontally with a velocity \sqrt{\left(\frac{1}{2} a g\right)} from the highest point of the outside of a fixed smooth sphere of radius a.Show that it will leave the sphere at the point whose vertical distance below the point of projection is \frac{a}{6}.)
Solution-

गति के समीकरण हैं-

v^{2}=u^{2}+2 a g-2 a g \cos \theta....(1) \\ R=\frac{m}{a} \cdot\left[3 a g \cos \theta-2 a g-u^{2}\right]...(2)
यहां u^{2}=\frac{1}{2}ag \\ \therefore R=\frac{m}{a}\left[3 a g \cos \theta-2 a g-\frac{1}{2} a g\right] \\ R=\frac{m}{a} [ 3 a g \cos \theta-\frac{5}{2} a g]
जब कण वृत्त को छोड़ेगा तो R=0

\frac{m}{a}[3 a g \cos \theta-\frac{5}{2} a g \cos \theta]=0 \\ \Rightarrow \quad\left(-3 ag \cos \theta-\frac{5}{2}\right)=0 \\ \Rightarrow \quad \cos \theta=\frac{5}{6}
केन्द्र से ऊपर P की ऊंचाई=ON=a \cos \theta \\ =a\left(\frac{5}{6}\right) =\frac{5a}{6}
सर्वोच्च ऊंचाई से उर्ध्वाधर दूरी=a-\cos \theta \\ =a-\frac{5}{6}a \\ =(\frac{a}{6})
Example-3.एक भारी कण 27a त्रिज्या के किसी चिकने ऊर्ध्वाधर वृत्त से नीचे की ओर विराम से उच्चत्तम बिन्दु से फिसलता है। सिद्ध करो कि वृत्त को छोड़ने पर वह 16a नाभिलम्ब वाले परवलय में चलने लगेगा।
(A heavy particle is allowed to slide down a smooth vertical circle of radius 27a from rest the highest point.Show that on leaving the circle it will move in a parabola of latus rectum 16a.)
Solution-

गति के समीकरण होंगे-

v^{2}=u^{2}+2ag=-2ag \cos \theta \\ R=\frac{m}{a} [3 a g \cos \theta-2 a g-u^{2}]
यदि त्रिज्या 27a हो तो गति के समीकरण होंगे-

v^{2}=u^{2}+54 a g-54 a g \cos \theta \\ u=0 \\ v^{2}=54 a g \cos \theta-54 a g \cos \theta \\ v^{2}=54ag (1-\cos \theta)....(1) \\ R=\frac{m}{27 a}\left[81ag \cos \theta-54 a g-u^{2}\right] \\ u=0 \\ \Rightarrow R=\frac{m}{27a}[81 a g \cos \theta-54 a g] \\ \Rightarrow R=m g(3 \cos \theta-2)....(2)
जब कण गोले को P बिन्दु पर छोड़ेगा तो R=0

\cos \theta=\frac{2}{3}\cdots(3) \\ v^{2}=54 a g-54ag(\frac{2}{3})=18 a g
उर्ध्वाधर दूरी गिर चुका है जब यह P बिन्दु पर पहुंचता है
=BN=BO-ON

=27a-27 a \cos \theta \\ =27a -27(\frac{2}{3}) a \\ =27 a-18 a \\ =9 a
वृत्त को छोड़ने पर यह परवलय पथ v वेग से क्षैतिज के साथ \theta कोण बनाते हुए तय करेगा
परवलय का नाभिलम्ब (L.R.)=\frac{2 v^{2} \cos ^{2} \theta}{g} \\ \frac{2}{g} \cdot 18 a g \cdot \frac{4}{9} \\ =16a

उपर्युक्त विवरण के द्वारा एक चिकने ऊर्ध्वाधर वृत्त के बाहर की ओर गति (Motion Outside Soomth Vertical Circle),एक चिकने ऊर्ध्वाधर वृत्त या गोले के बाहर की ओर कण की गति (Motion of a Particle on Outside of a Smooth Vertical Circle or Sphere) को समझ सकते हैं।
Example-4. एक कण किसी स्थिर चिकने गोले के बाहरी तल के बिन्दु A से विरामावस्था से नीचे की ओर फिसलता है। यदि बिन्दु A केन्द्र की सतह से h ऊंचाई पर हो तो सिद्ध करो कि कण गोले को इस सतह से ऊंचाई पर छोड़ देगा।
(A particle starts from rest from a point A of a fixed smooth sphere,If the height of A above the level of the centre be h,then show that the particle will leave the sphere at a height above the level.)
Solution- माना कि कण बिन्दु C से प्रारम्भ होता है जहां \theta=\alpha ताकि इसकी O से ऊपर ऊंचाई ON=a.इससे नीचे वह बिन्दु जिसकी ऊंचाई h है केन्द्र O से h-a \cos \alpha   ऊपर होगा। इसलिए प्रारम्भिक वेग जहां कण C से प्रारम्भ करता है,गिर चुका है h-a \cos \alpha \\ u=\sqrt{[2 g(h-a \cos \alpha)]}

गति के समीकरण हैं-

m \frac{d^{2} s}{d t^{2}}=mg \sin \theta
तथा \frac{m v^{2}}{a}=m g \cos \theta-R \\ v \frac{d v}{d s}=g \sin \theta \\ \Rightarrow v dv=g \sin \theta \frac{d s}{d \theta} \cdot d \theta
समाकलन करने पर-

v^{2}=-2 a g \cos \theta+A

\theta=\alpha, v^{2}=2g(h-a \cos \alpha) \\ 2g(h-a \cos \alpha)=-2a \cos \alpha+A \\ A=2gh \\ v=2gh-2ga \cos \theta...(1) \\ R=m g \cos \theta-m \frac{v^{2}}{a} \\=mgcos \theta-\frac{m}{a} (2gh-2 g a \cos \theta) \\ =\frac{m}{a}[2 a g \cos \theta-2 g h]
कण वृत्त को छोड़ेगा P पर तब R=0

\frac{m}{a}[2 a \cos \theta-2 g h]=0 \\ \Rightarrow a \cos \theta=\frac{2}{3} h \\ \Rightarrow OM=\frac{2}{3} h
अतः O से ऊपर ऊंचाई=OM=\frac{2}{3} h
Example-5. एक कण a त्रिज्या वाले चिकने गोले के उच्चत्तम बिन्दु से \frac{1}{2} \sqrt{(a g)} वेग से प्रक्षिप्त किया जाता है।ज्ञात कीजिए कि यह गोले के तल को कहां छोड़ेगा तथा यह सिद्ध कीजिए कि गोले के केन्द्र से गुजरने वाले क्षैतिज समतल को केन्द्र से \frac{9 \sqrt{39}+7 \sqrt{7} a}{64} दूरी पर टकराएगा।
(A body is projected along the surface of a smooth sphere of radius a from the highest point with velocity \frac{1}{2} \sqrt{(a g)}.Find where it will leave the surface and prove that it will strike a horizontal plane through the centre of the sphere at a distance \frac{9 \sqrt{39}+7 \sqrt{7} a}{64} from the centre.)
Solution-

गति के समीकरण होंगे-

v^{2}=u^{2}+2ag=-2ag \cos \theta....(1) \\ R=\frac{m}{a} [3 a g \cos \theta-2 a g-u^{2}]...(2)
कण वृत्तीय पथ को छोड़ेगा जब R=0

\cos \theta =\frac{u^{2}+2 a g}{3 a g} \\ =\frac{\frac{1}{4} a g+2 a g}{3 a g} \\ =\frac{3}{4} \\ \therefore u^{2}=\frac{1}{4} a g \\ v^{2} =\frac{1}{4} a g+2 a g-2 a g \cdot\left(\frac{3}{4}\right) \\ =\frac{3}{4} a g
यह कण जब वृत्तीय पथ को छोड़ेगा तब वेग होगा,वृत्तीय पथ को छोड़ने के बाद कण परवलय पथ तय करेगा जो क्षैतिज के साथ \theta कोण बनाता है। जहां \cos \theta=\frac{3}{4} \\ \sin \theta=\frac{\sqrt{7}}{4}, \tan \theta=\frac{\sqrt{7}}{3}
बिन्दु P(x,y) के निर्देशांक x=AN तथा y=PN=a \cos \theta=\frac{3}{4}a
A बिन्दु परवलय पथ पर है जिसकी समीकरण है

y=x \tan \theta-\frac{1}{2} \frac{(-g) x^{2}}{v^{2} \cos ^{2} \theta}
ऋणात्मक चिन्ह y-अक्ष से नीचे की ओर गति करने के कारण लिया गया है-

\frac{3}{4} a=x{\frac{\sqrt{7}}{3}}+\frac{1}{2} g-\frac{x^{2}}{\frac{3 a g}{4} \cdot \frac{9}{16}} \\ \Rightarrow 32 x^{2}+9 \sqrt{7} x-\frac{81}{4} a^{2}=0 \\ 32 x^{2}+9 \sqrt{7} x-\frac{81}{4} a^{2}=0 \\ \Rightarrow x=\frac{(-9 \sqrt{7}) a \pm a \sqrt{\left(81 \times 7+4 \times 32 \cdot \frac{81}{4}\right)}}{2 \times 32} \\ \Rightarrow x=\frac{-91 \sqrt{7}+9 \sqrt{39}}{64}a=NA \\ OA =ON+NA \\ =sin \theta+ x \\ =\frac{a\sqrt{7}}{4}+\frac{9 \sqrt{39}-9 \sqrt{7}}{64} a \\ \Rightarrow OA=\left(\frac {7 \sqrt{7}+9 \sqrt{39}) }{64}\right)a

उपर्युक्त विवरण के द्वारा एक चिकने ऊर्ध्वाधर वृत्त के बाहर की ओर गति (Motion Outside Soomth Vertical Circle),एक चिकने ऊर्ध्वाधर वृत्त या गोले के बाहर की ओर कण की गति (Motion of a Particle on Outside of a Smooth Vertical Circle or Sphere) को समझ सकते हैं।
Example-6. एक m द्रव्यमान वाला भारी कण चिकनी वृत्ताकार नली में,जो एक उर्ध्वाधर समतल में बद्ध है,पूरे चक्कर लगाता है उसका महत्तम वेग न्यूनतम वेग का n गुणा है। सिद्ध कीजिए कि नली में उस समय दाब जबकि कण ऊर्ध्वाधर दिशा में चल रहा है, 2mg \sqrt {(\frac{n^{2}+1}{n^{2}-1})} है तथा उस समय कण का वेग उच्चत्तम बिन्दु पर वेग का \sqrt {\frac{a}{2}\left(n^{2}+1\right)} गुणा है।
(A heavy particle of mass complete revolution in a smooth circular tube fixed in a vertical plane.Its greatest speed is n time its least speed.Prove that the pressure in the tube when the particle is moving vertically is 2mg \sqrt {(\frac{n^{2}+1}{n^{2}-1})} and that its speed then is \sqrt {\frac{a}{2}\left(n^{2}+1\right)} times its speed at the highest point.)
Solution- माना निम्नत्तम बिन्दु से प्रक्षेप वेग u है जो अधिकतम है तथा सर्वोच्च बिन्दु B पर इसका वेग V है तब
u=nV …..(1)

अतः गति के समीकरण होंगे

v^{2}=u^{2}-2 a g(1-\cos \theta).....(2) \\ R=\frac{m}{a} [3 a g \cos \theta-2 a g-u^{2}]....(3)
\theta=180 और v=V समीकरण (2) में रखने पर-

V^{2}=u^{2}-2 a g[1-(-1)] \\ \Rightarrow \frac{u^{2}}{n^{2}}=u^{2}-4 a g \quad[(1) से ] \\ \Rightarrow 4 a g=u^{2}\left(\frac{n^{2}-1}{n^{2}}\right) \cdots(4)
बिन्दु C पर कण की त्रिज्या उर्ध्वाधर व्यास के साथ \theta=90 कोण बनाता है

R =\frac{m}{a}\left[u^{2}-2 a g+3 a g \cos 90^{\circ}\right] \\ =\frac{m}{a}\left[u^{2}-2 a g \right] \\ =\frac{m u^{2}}{a}-2 m g \\=m\frac{4 g n^{2}}{n^{2}-1}-2 m g \\ R=2 m g \cdot \frac{\left(n^{2}+1\right)}{\left(n^{2} -1\right)}
पुनः समीकरण (2) में \theta=90 रखने पर-

v^{2}=u^{2}-2 a g\left(1-\cos 90\right) \\ u^{2}-2 a g=u^{2}-\frac{u^{2}(3 n^{2}-1)}{2 n^{2}} \quad[(4) से ]  \\ v^{2}=\frac{u^{2}}{2 n^{2}} \left(n^{2}+1\right) \\ v^{2}=\left(\frac{n^{2}+1}{2}\right) V^{2} \quad[(1) से] \\ u^{2}=\sqrt{\left(\frac{n^{2}+1}{2}\right)} V
उपर्युक्त विवरण के द्वारा एक चिकने ऊर्ध्वाधर वृत्त के बाहर की ओर गति (Motion Outside Soomth Vertical Circle),एक चिकने ऊर्ध्वाधर वृत्त या गोले के बाहर की ओर कण की गति (Motion of a Particle on Outside of a Smooth Vertical Circle or Sphere) को समझ सकते हैं।

3.एक चिकने ऊर्ध्वाधर वृत्त के बाहर की ओर गति की समस्याएं (Motion Outside Soomth Vertical Circle Problems),एक चिकने ऊर्ध्वाधर वृत्त या गोले के बाहर की ओर कण की गति की समस्याएं (Motion of a Particle on Outside of a Smooth Vertical Circle or Sphere Problems)-

(1.)एक कण एक चिकने ऊर्ध्वाधर वृत्त जिसकी त्रिज्या a है,के उच्चत्तम बिन्दु पर रखा गया है।यह कण उपेक्षणीय गति से चलना प्रारम्भ कर नीचे की ओर सरकता है। सिद्ध कीजिए कि जिस समय यह वृत्त को छोड़ता है,उस समय तक यह त्रिज्या की लम्बाई की एक-तिहाई उर्ध्वाधर दूरी तय कर चुकता है।
(A particle is placed at the highest point of a smooth vertical circle of radius a and is allowed slide down starting with a negligible velocity.Prove that it will leave the circle after describing vertically a distance equal to one-third of the radius.)
(2.)एक कण ऊर्ध्वाधर वृत्त की बाहरी सतह पर फिसल रहा है।इसका प्रारम्भिक वेग प्रारम्भिक बिन्दु पर केन्द्र के ऊपर h ऊंचाई से इस बिन्दु तक गिरने पर प्राप्त वेग के बराबर हो तो सिद्ध करो कि यह केन्द्र से (\frac{2}{3}h) ऊंचाई पर वृत्त से छोड़ देगा।
(A particle moves under gravity in a vertical circle,sliding down the convex side of smooth circular arc.If its initial velocity is that due to a fall to the starting point from a height h above the centre;Show that it will fly off the circle when a height (\frac{2}{3}h) above the centre.)
(3.) एक भारी कण ऊर्ध्वाधर तल में r त्रिज्या वाले एक चिकने वृत्तीय ट्यूब के अन्दर गुरुत्वाकर्षण के अधीन नीचे की ओर फिसलता है,यदि वह उच्चत्तम बिन्दु से \sqrt{2ga} वेग से रवाना होता है तो सिद्ध करो कि जहां त्वरण का उर्ध्वाधर घटक अधिकतम होता है, वहां वक्र की प्रतिक्रिया कण के भार की दो गुणा होती है।
(A particle slides under gravity down the inside of a smooth circular tube held in a vertical plane.It starts from the highest point with a velocity \sqrt{2ga}, where a is the radius of circle.Prove that when in the subsequent motion the vertical component of its acceleration is maximum,the pressure on the curve is equal to twice the weight of the particle.)
उपर्युक्त विवरण में एक चिकने ऊर्ध्वाधर वृत्त के बाहर की ओर गति (Motion Outside Soomth Vertical Circle),एक चिकने ऊर्ध्वाधर वृत्त या गोले के बाहर की ओर कण की गति (Motion of a Particle on Outside of a Smooth Vertical Circle or Sphere) के बारे में बताया गया है।

4.ऊर्ध्वाधर वृत्त में गति क्या है? (What is motion in vertical circle?)-

किसी ऊर्ध्वाधर वृत्त में किसी पिंड की गति का अध्ययन करते समय हमें गुरुत्वाकर्षण के प्रभाव पर विचार करना होगा।पृथ्वी के गुरुत्वाकर्षण क्षेत्र के प्रभाव के कारण, बाॅडी के वेग के परिमाण और स्ट्रिंग में तनाव लगातार बदलते रहते हैं।इसलिए ऊर्ध्वाधर सर्कल में गति एक समान वृत्तीय गति नहीं है।

5.कब एक कण ऊर्ध्वाधर सर्कल में घूमता है? (When a particle is moving in vertical circle?)-

असमान वृत्तीय गति में, वेग की दिशा में परिवर्तन के कारण केन्द्रीय त्वरण उत्पन्न होता है।

6.ऊर्ध्वाधर वृत्तीय गति के प्रकार क्या हैं? (What are the types of vertical circular motion?)-

लंबवत वृत्ताकार गति
रोलर कोस्टर।
पानी की बाल्टी।
पहाड़ी रास्तों पर यात्रा करती कारें।

7.वृत्तीय गति के 3 उदाहरण क्या हैं? (What are the 3 examples of circular motion?)-

वृत्तीय गति के उदाहरणों में शामिल हैं: एक कृत्रिम उपग्रह जो लगातार ऊंचाई पर पृथ्वी की परिक्रमा कर रहा है,एक हब के चारों ओर घूमता हुआ एक छत का पंखा,एक पत्थर जो एक रस्सी से बंधा है और हलकों में झुला जा रहा है, एक दौड़ में एक वक्र के माध्यम से मोड़ने वाली कार ट्रैक, एक इलेक्ट्रॉन एक समान चुंबकीय क्षेत्र के लिए लंबवत घूम रहा है।

8.ऊर्ध्वाधर सर्कल में सबसे निम्नत्तम बिंदु पर वेग (Velocity at lowest point in vertical circle)-

यदि बाॅडी का वेग 'v' ऐसा है,√2gr तो बाॅडी बिंदु L, ऊर्ध्वाधर वृत्त के निम्नतम बिंदु के पास में दोलन करता है। यदि बाॅडी का वेग 'v' ऐसा है जो √2gr <v <√5gr है,तो बाॅडी वृत्तीय मार्ग को छोड़ देता है और प्रक्षेप्य की तरह कार्य करता है।यह M और H के बीच वृत्तीय गति को छोड़ देगा। जहां M क्षैतिज व्यास पर तथा M उर्ध्वाधर व्यास पर उच्चत्तम बिन्दु है।

9.टाॅप पर लंबवत वृत्तीय गति (Vertical circular motion velocity at top),ऊर्ध्वाधर सर्कल में बाॅडी की गति (Motion of a body in vertical circle)-

बाॅडी के वेग की अभिव्यक्ति एक वर्टिकल सर्कल में चलती है।इसलिए बाॅडी की गति लगातार बदलती रहती है।यह निम्नत्तम बिन्दु की स्थिति में अधिकतम है और ऊर्ध्वाधर सर्कल के उच्चत्तम बिन्दु के स्थान पर न्यूनतम है।अतः बाॅडी की गति एकसमान वृत्तीय गति नहीं है।

10.ऊर्ध्वाधर वृत्तीय गति में न्यूनतम गति (Vertical circular motion minimum speed),ऊर्ध्वाधर सर्कल में गति (Motion in vertical circle)-

इसलिए बाॅडी की गति लगातार बदलती रहती है।यह निम्नत्तम बिन्दु की स्थिति में अधिकतम है और ऊर्ध्वाधर सर्कल के उच्चत्तम बिन्दु की स्थान पर न्यूनतम है।अतः बाॅडी की गति एकसमान वृत्तीय गति नहीं है।

11.ऊर्ध्वाधर वृत्तीय गति में अधिकतम तनाव (Maximum tension in vertical circular motion)-

निम्नत्तम बिन्दु पर पर स्ट्रिंग में तनाव अधिकतम है।सबसे ऊपरी बिंदु पर, केन्द्रापसारक बल ऊर्ध्वाधर रूप से ऊपर की ओर कार्य करता है और बाॅडी का वजन लंबवत रूप से नीचे की ओर कार्य करता है।इस प्रकार स्ट्रिंग में तनाव न्यूनतम है।
उपर्युक्त प्रश्नों के उत्तर, उदाहरणों तथा सवालों को हल करके एक चिकने ऊर्ध्वाधर वृत्त के बाहर की ओर गति (Motion Outside Soomth Vertical Circle),एक चिकने ऊर्ध्वाधर वृत्त या गोले के बाहर की ओर कण की गति (Motion of a Particle on Outside of a Smooth Vertical Circle or Sphere) को ठीक से समझ सकते हैं।

Also Read This Article:-Simple Harmonic Motion Formula

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Instagram	click here
4.	Linkedin	click here
5.	Facebook Page	click here