Moment of Inertia in Dynamics
1.गतिविज्ञान में जड़त्व आघूर्ण (Moment of Inertia in Dynamics),जड़त्व आघूर्ण (Moment of Inertia):
गतिविज्ञान में जड़त्व आघूर्ण (Moment of Inertia in Dynamics) के इस आर्टिकल में किसी कण अथवा ठोस पिण्ड का किसी रेखा के परितः जड़त्व आघूर्ण ज्ञात करना सीखेंगे।इस पर आधारित कुछ सवालों के हल निम्न हैं:
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Apse in Dynamics
2.गतिविज्ञान में जड़त्व आघूर्ण के साधित उदाहरण (Moment of Inertia in Dynamics Solved Examples):
Example:1.एक समबाहु त्रिभुज के आधार के परितः जड़त्व-आघूर्ण ज्ञात करिए।
(Find the M. I. of an equilateral triangle about its base.)
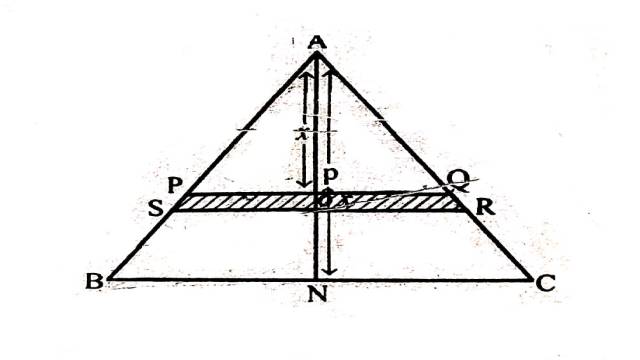
Solution:माना ABC दी हुई समबाहु त्रिभुज है और यह भी माना कि हमें का भुजा BC के परितः जड़त्व आघूर्ण ज्ञात करना है।इसके लिए पटल का BC के समान्तर पतली पट्टियों में विभाजित करते हैं।
माना PQRS पटल की एक ऐसी पतली पट्टी है जो A से x दूरी पर तथा \delta x चौड़ाई की है।माना BC=2a तथा A से BC पर लम्ब AN खींचा।
समबाहु त्रिभुज में BN=a
समकोण \triangle ANB में
AN^2=(A B)^2-(B N)^2 \\ =(2 a)^2-(a)^2 \\ =4 a^2-a^2 \\ =3 a^2 \\ \Rightarrow AN=\sqrt{3} a \\ \triangle APQ \sim \triangle ABC \\ \Rightarrow \frac{P Q}{B C}=\frac{AP}{AN} \quad[\because AP=x] \\ \Rightarrow \frac{P Q}{2 a}=\frac{x}{\sqrt{3} a} \\ \Rightarrow P Q=\frac{2 x}{\sqrt{3}} \\ \triangle ABC
के एकांक क्षेत्रफल की संहति =\frac{M}{\frac{1}{2} \times 2 a \times \sqrt{3}a} \\ =\frac{M}{\sqrt{3} a^2}
पतली पट्टी PQ की संहति=\frac{M}{\sqrt{3} a^2} \cdot PQ \cdot \delta x \\ =\frac{M}{\sqrt{3} a^2} \times \frac{2 x}{\sqrt{3}} \cdot \delta x
पतली पट्टी PQ का BC के परितः जड़त्व-आघूर्ण =\frac{2 M}{3 a^2} x \cdot \delta x (\sqrt{3} a-x)^2
अतः समबाहु \triangle ABC का BC के परितः जड़त्व आघूर्ण=\int_0^{\sqrt{3} a} \frac{2 M}{3 a^2}(\sqrt{3}a-x)^2 x dx \\ =\int_0^{\sqrt{3} a} \frac{2 M}{3 a^2}\left(3 a^2 x-2 \sqrt{3} a x^2+x^3\right) d x \\ =\frac{2 M}{3 a^2}\left[\frac{3 a^2 x^2}{2}-\frac{2 \sqrt{3} a x^3}{3}+\frac{x^4}{4}\right]_0^{\sqrt{3} a} \\ =\frac{2 M}{3 a^2}\left[\frac{3 a^2}{2} \times 3 a^2-\frac{2 \sqrt{3} a}{3}\left(3 \sqrt{3} a^3\right) +\frac{ 9 a^4}{4}\right] \\ =\frac{2 M}{3 a^2}\left[\frac{9 a^4}{2}-\frac{6 a^4}{1}+\frac{9 a^4}{4}\right] \\ =\frac{2 M}{3 a^2} \left[\frac{18 a^4-24 a^4+9 a^4}{4}\right] \\ =\frac{2 M}{3 a^2} \times \frac{3 a^4}{4} \\ =\frac{1}{2} M a^2
Example:2.ABC एक समान समबाहु त्रिभुजाकार पटल है जिसकी संहति M तथा भुजा की लम्बाई a है।कोण A के समद्विभाजक के परितः इसका जड़त्व आघूर्ण ज्ञात कीजिए।
Solution:माना ABC दी हुई समबाहु त्रिभुज है और यह भी माना कि हमें के समद्विभाजक के परितः जड़त्व आघूर्ण ज्ञात करना है।इसके लिए पटल को BC के समान्तर पतली पट्टीयों में विभाजित करते हैं।
माना PQRS पटल की एक ऐसी पतली पट्टी है जो A से x दूरी तथा \delta x चौड़ाई की है।AB=BC=CA=a है तथा A से BC पर लम्ब AN लम्ब है तो समबाहु त्रिभुज में BN=\frac{a}{2}
समकोण \triangle A N B में
A N^2=A B^2-B N^2 \\ =a^2-\left(\frac{a}{2}\right)^2 \\ =\frac{4 a^2-a^2}{4} \\ \Rightarrow A N =\frac{\sqrt{3}}{2} a \\ \triangle A P Q \sim \triangle A B C \\ \frac{P Q}{B C} =\frac{A P}{A N} \\ \Rightarrow \frac{P Q}{a} =\frac{x}{\frac{\sqrt{3}}{2} a} \\ \Rightarrow P Q =\frac{2 x}{\sqrt{3}} \\ \triangle ABC के एकांक क्षेत्रफल की संहति =\frac{M}{\frac{1}{2} \times a \times \frac{\sqrt{3}}{2} a} \\ \left[\because \operatorname{area}(\triangle ABC)=\frac{1}{2} \times B C \times A N\right] \\ =\frac{4 M}{\sqrt{3}a^2}
पतली पट्टी PQ की संहति=\frac{4 M}{\sqrt{3} a^2} \cdot P Q \cdot \delta x \\ =\frac{4 M}{\sqrt{3} a^2} \times \frac{2 x}{\sqrt{3}} \cdot \delta x \\ =\frac{8 M x}{3 a^2} \cdot \delta x
पतली पट्टी PQ का लम्ब AN (कोण A के समद्विभाजक) के परितः जड़त्व आघूर्ण=\frac{1}{3}\left(\frac{1}{2} PQ \right)^2 \cdot \frac{8 M x}{3 a^2} \delta x \\=\frac{1}{12} \times\left(\frac{2 x}{\sqrt{3}}\right)^2 \times \frac{8Mx}{3 a^2} \cdot \delta x \\ =\frac{2}{9 a^2} \times \frac{4}{3} M x^3 \cdot \delta x \\ =\frac{8}{27 a^2} M x^3 \delta x
अतः समबाहु \triangle ABC का कोण A के लम्ब समद्विभाजक के परितः जड़त्व आघूर्ण =\frac{8M}{27 a^2} \int_0^{\frac{\sqrt{3}}{2} a} x^3 d x \\ =\frac{8}{27 a^2} M\left[\frac{x^4}{4}\right]_0^{\frac{\sqrt{3}}{2} a} \\ =\frac{8}{27} a^2 M \times \frac{1}{4} \times \frac{9 a^4}{16} \\ =\frac{1}{24} M a^2
Example:3.सिद्ध करो कि M संहति के एक समद्विबाहु त्रिभुज ABC के शीर्ष A में होकर जानेवाली (i) a लम्बाई की सम्मुख भुजा के लम्ब किसी अक्ष के परितः जड़त्व आघूर्ण \left(\frac{Ma^2}{24} \right ) होता है।
(ii)उसके तल के लम्ब रेखा के परितः जड़त्व आघूर्ण \frac{M a^2}{8}\left(\frac{1}{3}+\cot ^2 \frac{A}{2}\right) होता है।
(Prove that the M. I. of an isosceles about an axis through the vertex A perpendicular to (i) the opposite side of length a is
(ii)the plane of triangle is
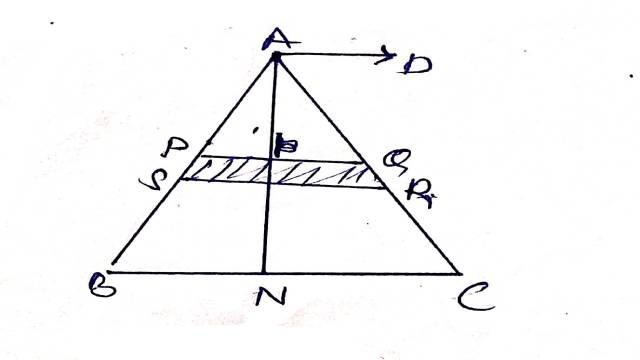
Solution:माना ABC दी हुई समद्विबाहु त्रिभुज है और यह भी माना कि हमें सम्मुख भुजा BC और उसके तल के लम्ब रेखा के परितः जड़त्व आघूर्ण ज्ञात करना है।इसके लिए पटल को BC के समान्तर पतली पट्टीयों में विभाजित करते हैं।
माना PQRS पटल की एक ऐसी पतली पट्टी है जो A से x दूरी तथा \delta x चौड़ाई की है।AB=BC=CA=a है तथा BC पर लम्ब AN खींचा।AN,का समद्विभाजक है तथा BN=\frac{a}{2}
समद्विबाहु त्रिभुज \triangle ABN में
\cot \frac{A}{2}=\frac{A N}{B N} \\ \Rightarrow A N=\frac{a}{2} \cot \frac{A}{2} \\ \triangle ABC के एकांक क्षेत्रफल की संहति
=\frac{M}{\frac{1}{2} \times B C \times A N} \\ =\frac{M}{\frac{1}{2} \times a \times \frac{a}{2} \cot \frac{A}{2}} \\ =\frac{4 M}{a^2 \cot \frac{A}{2}}
पतली पट्टी PQ की संहति=\frac{4 M}{a^2 \cot \frac{A}{2} } \cdot PQ \cdot \delta x \\ =\frac{4 M}{a^2 \cot \frac{A}{2}} \cdot PQ \cdot \delta x \\ \triangle APQ \sim \triangle ABC \\ \frac{PQ}{BC} =\frac{AP}{AN} \\ \Rightarrow P Q =\frac{a \times x}{\frac{a}{2} \cot \frac{A}{2}}=\frac{2 x}{\cot \frac{A}{2}}
पतली पट्टी PQ की संहति=\frac{4 M}{a^2 \cot \frac{A}{2}} \times \frac{2 x}{\cot \frac{A}{2}} \cdot \delta x \\ =\frac{8 M x}{a^2 \cot ^2 \frac{A}{2}} \cdot \delta x
(i) पतली पट्टी PQ का BC के लम्बवत AN के परितः जड़त्व आघूर्ण= \frac{8 Mx}{a^2 \cot ^2 \frac{A}{2}} \cdot \delta x \times \frac{1}{3} \left(\frac{PQ}{2}\right)^2
अतः समद्विबाहु \triangle ABC का BC के परितः जड़त्व आघूर्ण=\frac{8 M}{3 a^2 \cot ^2 \frac{A}{2}} \int_0^{\frac{a}{2} \cot \frac{A}{2}} x\left(\frac{x}{\cot \frac{A}{2}}\right)^2 dx \\ =\frac{8 M}{3 a^2 \cot ^2 \frac{A}{2}} \times \frac{1}{\cot ^2 \frac{A}{2}}\left[\frac{x^4}{4}\right]_0^{\frac{a}{2} \cot \frac{A}{2}} \\ =\frac{8M}{12 a^2 \cot \frac{A}{2}} \times \frac{a^4}{16} \cot^4 \frac{A}{2} \\ =\frac{1}{24} M a^2
(ii)समद्विबाहु \triangle ABC के तल के लम्ब रेखा AD के परितः जड़त्व आघूर्ण=PQ के मध्य बिन्दु के परितः जड़त्व आघूर्ण+पट्टी का द्रव्यमान× AP^2 \\ =\int_0^{\frac{a}{2} \cot \frac{A}{2}} \frac{8 M x \delta x}{a^2 \cos ^2 \frac{A}{2}}\left[\frac{1}{3} \cdot\left(\frac{P Q}{2}\right)^2+A P^2\right] \\ =\int_0^{\frac{a}{2} \cot \frac{A}{2}} \frac{8Mx}{a^2 \cot ^2 \frac{A}{2}}\left[\frac{x^3}{3 \cot ^2 \frac{A}{2}}+x^3\right] d x \\ =\frac{8 M}{a^2 \cot ^2 \frac{A}{2}} \int_0^{\frac{a}{2} \cot \frac{A}{2}}\left[\frac{x^3}{3 \cot ^2 \frac{A}{2}}+x^3\right] d x \\ =\frac{8 M}{a^2 \cot ^2 \frac{A}{2}} \left[\frac{x^4}{12 \cot ^2 \frac{A}{2}}+\frac{1}{4} \cdot x^4\right]_0^{\frac{a}{2} \cot \frac{A}{2}} \\=\frac{8 M}{4 a^2 \cot ^2 \frac{A}{2}}\left[\frac{1}{3 \cot ^2 \frac{A}{2}} \cdot \frac{a^4 \cot ^4 \frac{A}{2}}{16}+\frac{a^4 \cot^4 \frac{A}{2}}{16}\right] \\ = \frac{2 M}{a^2 \cot ^2 \frac{A}{2}} \times \frac{1}{16}\left[\frac{a^4 \cot ^2 \frac{A}{2}}{3}+a^4 \cot ^4 \frac{A}{2}\right] \\=\frac{M}{8 a^2} \times \frac{a^4}{\cot ^2 \frac{A}{2}}-\cot ^2 \frac{A}{2} \left[\frac{1}{3}+\cot ^2 \frac{A}{2}\right] \\=\frac{1}{8} M a^2\left(\frac{1}{3}+\cot ^2 \frac{A}{2}\right)
Example:4.सिद्ध करो कि एक परवलय-क्षेत्र जिसका नाभिलम्ब 4a है,के उस भाग का जड़त्व-आघूर्ण जो उसके शीर्ष से h दूरी पर किसी द्विकोटि द्वारा काटा जाता है,शीर्ष पर खींची गई स्पर्शी के सापेक्ष \left(\frac{3}{7}\right) Mh^2 तथा अपने अक्ष के सापेक्ष \frac{4}{5} Mah होता है।
(Show that the M. I. of a parabolic area of L. R. 4a cut off by a double ordinate at a distance h from the vertex is \left(\frac{3}{7}\right) Mh^2 about the tangent at the vertex and \frac{4}{5} Mah about the axis.)
Solution:माना परवलय का समीकरण
y^2=4a x \cdots(1)
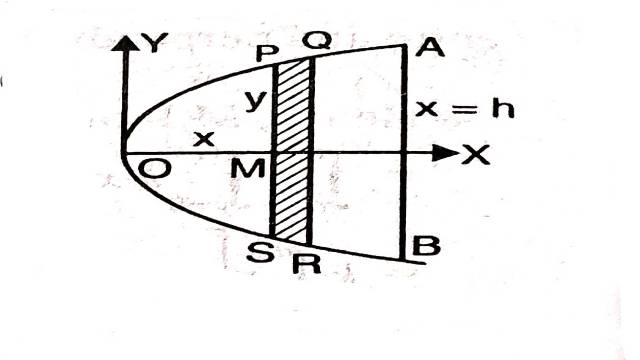
माना परवलय शीर्ष से h दूरी पर द्विकोटि AB द्वारा काटा गया भाग AOB है।प्रारम्भिक पतली पट्टी PQRS, OY के समान्तर है जो शीर्ष O से x दूरी है तथा \delta x चौड़ाई है और P के निर्देशांक (x,y) है।AOB भाग का द्रव्यमान M है
M=\int_0^h 2 y \rho d x \\ =2 \rho \int_0^h \sqrt{4 a x} d x\left[\because y^2=4ax\right] \\ =4 \rho \int_0^h a^{\frac{1}{2}} x^{\frac{1}{2}} d x \\ =4 \rho a^{\frac{1}{2}}\left[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right]_0^h \\ =\frac{8}{3} \rho a^{\frac{1}{2}} h^{\frac{3}{2}} \\ \Rightarrow \rho=\frac{3 M}{8 a^{\frac{1}{2}}h^{\frac{3}{2}}}
पतली पट्टी का स्पर्शी OY के सापेक्ष जड़त्व आघूर्ण=x^2 2 \rho y \delta x \\ =2 x^2 \cdot \frac{3 M}{8 a^{\frac{1}{2}} h^{\frac{3}{2}}} \times \sqrt{4ax} \delta x \\ =\frac{3 M x^{\frac{5}{2}}}{2 h^{\frac{3}{2}}} \delta x
AOB क्षेत्र का स्पर्शी OY के सापेक्ष जड़त्व आघूर्ण =\int_0^h \frac{3 M x^{\frac{5}{2}}}{2 h^{\frac{3}{2}}} d x \\ =\frac{3 M}{h^{\frac{3}{2}}}\left[x^{\frac{7}{2}}\right]_0^h \\ =\frac{3 M}{2 h^{\frac{3}{2}}} \cdot \frac{h^{\frac{7}{2}}}{\frac{7}{2}} \\ =\frac{3}{7} M h^2
PQRS पट्टी का OX के सापेक्ष जड़त्व आघूर्ण (जो पट्टिका के लम्बवत है तथा मध्य बिन्दु M से गुजरती है)
=\frac{1}{3} y^2 \rho y \delta x
अतः OAB क्षेत्र का OX अक्ष के सापेक्ष जड़त्व आघूर्ण =\int_0^h \frac{2}{3} \rho y^3 d x \\ =\frac{2}{3} \rho \int_0^h(4 a x)^{\frac{3}{2}} d x \\ =\frac{16}{3} \rho a^{\frac{3}{2}} \int_0^h x^{\frac{3}{2}} d x \\ =\frac{16}{3} \rho a^{\frac{3}{2}}\left[\frac{x^{\frac{5}{2}}}{\frac{5}{2}}\right]_0^h \\ =\frac{16}{3} \times \frac{2}{5} \rho a^{\frac{3}{2}} h^{\frac{5}{2}} \\ =\frac{32}{15} \rho a^{\frac{3}{2}} h^{\frac{5}{2}} \\ =\frac{32}{15} \times a^{\frac{3}{2}} h^{\frac{5}{2}} \cdot \frac{3M}{8 a^{\frac{1}{2}}h^{\frac{3}{2}}} \\ =\frac{4}{5} a^{(\frac{3}{2}-\frac{1}{2})} h^{\left(\frac{5}{2}-\frac{3}{2}\right)} M \\ =\frac{4}{5} a hM \\ =\frac{4}{5} Mah
Example:5.एक खोखले वृत्तीय बेलन का इसके अक्ष के परितः जड़त्व आघूर्ण ज्ञात करिए,जबकि बाह्य तथा अन्तः त्रिज्याएँ क्रमशः a तथा b है।
(Find the M. I. of a hollow circular cylinder about its axis,external and internal radii being a and b respectively.)
Solution:माना बेलन की ऊँचाई h तथा बाह्य और अन्तः त्रिज्याएँ a तथा b है तब
\rho=\frac{M}{\pi\left(a^2-b^2\right) h}
एक वृत्तीय चक्रिका पर विचार करें,जिसकी मोटाई \delta x तथा O से दूरी x है
चक्रिका की संहति=\pi\left(a^2-b^2\right) \cdot \frac{ M}{\pi\left(a^2-b^2\right) h} \delta x \\ =\frac{M}{h} \delta x
अतः चक्रिका का अक्ष के सापेक्ष जड़त्व आघूर्ण=\frac{M}{h} \cdot \delta x \cdot\left(\frac{a^2+b^2}{2}\right)
अतः खोखले बेलन का अक्ष के सापेक्ष जड़त्व आघूर्ण=\int_{\frac{h}{2}}^{\frac{h}{2}} \frac{M}{h}\left(\frac{a^2 +b^2}{2}\right) \delta x \\ = \frac{M}{h}\left(\frac{a^2+b^2}{2}\right)[x]_{-\frac{h}{2}}^{\frac{h}{2}} \\ = \frac{M}{h}\left(\frac{a^2+b^2}{2}\right) \times\left(\frac{h}{2}+\frac{h}{2}\right) \\ = \frac{M}{h} \left(\frac{a^2 +b^2}{2}\right) \times h \\ = \frac{1}{2} \cdot M\left(a^2+b^2\right)
Example:6.एक गोलाभ का परिक्रमण-अक्ष के परितः जड़त्व आघूर्ण ज्ञात करिए।
(Find the M. I. of a speroid about its axis of revolution.)
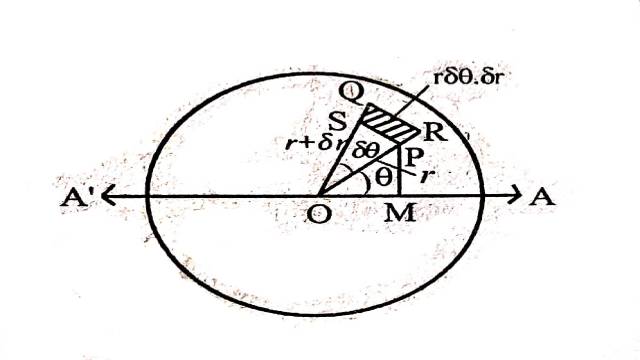
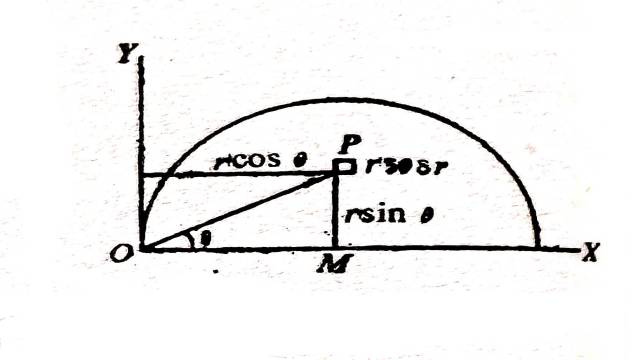
Solution:एक अल्प क्षेत्रफल (Elementary area) P(r,\theta) के परितः लें,जहाँ O वृत्त का केन्द्र तथा AOA’ इस वृत्त का व्यास है, तो OP=r तथा \angle POA=\theta
जब इस अवयव (PQRS क्षेत्रफल) को AA’ के परितः घुमाते हैं तो यह एक छल्ले (रिंग) को जनित करता है जिसका अनुप्रस्थ काट (cross section) r \delta \theta \delta r तथा इसकी त्रिज्या r \sin \theta होगी।
पुनः एकांक आयतन की संहति =\frac{M}{\frac{4}{3} \pi a^2}
अल्प छल्ले (रिंग) का आयतन=2 \pi r \sin \theta r \delta \theta \delta r
अल्प छल्ले (रिंग) का AOA’ के परितः जड़त्व आघूर्ण =\frac{3 M}{4 \pi r^3} \cdot (2 \pi r \sin \theta ) (r \sin \theta) r \delta \theta \delta r
ठोस गोले का अक्ष (व्यास AOA’) के परितः जड़त्व आघूर्ण=\int_0^\pi \int_0^a \frac{3 M}{4 \pi a^2}(2 \pi r \sin \theta)^2 (r \sin \theta)^2 r d \theta dr \\ =\frac{3 M}{2 a^2} \int_0^\pi\left[\frac{r^5}{5}\right]_0^a \sin ^3 \theta d \theta \\ =\frac{3}{10} M a^2 \cdot 2 \int_0^{\frac{\pi}{2}} \sin ^3 a d \theta \\ =\frac{3}{10} M a^2 \cdot 2 \cdot \frac{2}{3} \\ =\frac{2 M a^2}{5}
Example:7.एक अर्धवृत्तीय पटल का उसके सीमक व्यास तथा इसके सिरे पर स्पर्श रेखा के परितः जड़त्व गुणनफल ज्ञात करिए।
(Find the product of a semi-circular disc about the diameter and the tangent at its ends.)
Solution:O ध्रुव तथा OX प्रारम्भिक रेखा है तब r=2 a \cos \theta
एक कण पर विचार करें जिसका द्रव्यमान \rho है।इसकी अक्ष से दूरी अर्थात् व्यास और स्पर्शी इसके अन्त से r \sin \theta तथा r \cos \theta है अतः जड़त्व गुणन होगा=r \delta \theta \cdot \delta r \cdot \rho r \cos \theta \cdot r \sin \theta
सम्पूर्ण जड़त्व गुणन =\rho \int_0^{\frac{\pi}{2}} \int_0^{2 a \cos \theta} r^2 \sin \theta \cos a d \theta d r \\ =\rho \int_0^{\frac{\pi}{2}} \frac{(2 a \cos \theta)^4}{4} \cos \theta \sin \theta d \theta \\ =4 a^2 \rho \left[-\frac{\cos ^6 \theta}{6}\right]_0^{\frac{\pi}{2}} \\=\frac{2}{3} \rho a^4 \\ \therefore \text{P.I.}=\frac{2}{3} a^4 \cdot \frac{2 M}{\pi a^2}\left[\because M=\frac{1}{2} \pi a^2 \rho\right] \\ =\frac{4}{3 \pi} M a^2
उपर्युक्त उदाहरणों के द्वारा गतिविज्ञान में जड़त्व आघूर्ण (Moment of Inertia in Dynamics),जड़त्व आघूर्ण (Moment of Inertia) को समझ सकते हैं।
3.गतिविज्ञान में जड़त्व आघूर्ण की समस्याएँ (Moment of Inertia in Dynamics Problems):
(1.)एक आयताकार पटल का उसकी भुजा के परितः जड़त्व आघूर्ण ज्ञात कीजिए।
(Find the M. I. of a rectangular lamina about one of its sides.)
(2.) r^2=a^2 \cos^2 \theta से घिरे हुए क्षेत्रफल का जड़त्व-आघूर्ण इसके अक्ष के परितः ज्ञात कीजिए।
(Find the M. I. of the area bounded by r^2=a^2 \cos^2 \theta about its axis.)
Answer:-(1.) \frac{4}{3} M b^2
(2.) \frac{M a^2}{16}\left(\pi-\frac{8}{3}\right)
उपर्युक्त सवालों को हल करने पर गतिविज्ञान में जड़त्व आघूर्ण (Moment of Inertia in Dynamics),जड़त्व आघूर्ण (Moment of Inertia)को ठीक से समझ सकते हैं।
Also Read This Article:- Apsidal in Dynamics
4.गतिविज्ञान में जड़त्व आघूर्ण (Frequently Asked Questions Related to Moment of Inertia in Dynamics),जड़त्व आघूर्ण (Moment of Inertia) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.एक कण के एक रेखा के परितः जड़त्व आघूर्ण का सूत्र लिखो। (Write the Formula for the Moment of Inertia of a particle about a Line):
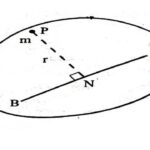
उत्तर:एक m संहति का कण तथा एक रेखा AB लो।माना कण की रेखा से लाम्बिक दूरी r, तब कण का रेखा AB के परितः जड़त्व आघूर्ण कहलाता है।अतः AB के परितः
जड़त्व आघूर्ण=(संहति) ×(लम्बवत दूरी)
M.I.=M r^2
प्रश्न:2.किसी पिण्ड की घूर्णन त्रिज्या कैसे ज्ञात करते हैं? (How is the Radius of Rotation of a Body Found?):

उत्तर:एक दृढ़ पिण्ड की संहति M है और एक K को इस प्रकार परिभाषित करते हैं कि
I=M K^2 \\ \Rightarrow K^2=\frac{1}{M}=\frac{\Sigma M r^2}{\Sigma M}
तब दृढ़ पिण्ड का रेखा AB के परितः परिभ्रमण अथवा घूर्णन त्रिज्या कहलाता है।
संतत संहति बंटन के लिए
K=\frac{\int r^2 d m}{\int d m}
प्रश्न:3.जड़त्व गुणन कैसे ज्ञात करते हैं? (How is Product of Inertia Calculated?):
उत्तर:माना OX तथा OY दो लम्ब निर्देशाक्ष हैं तथा यदि किसी पिण्ड के अवयव (Element) की संहति m तथा OX,OY के सापेक्ष निर्देशांक (x,y) हैं,पिण्ड OX,OY रेखाओं के परितः जड़त्व-गुणनफल कहलाता है।
उपर्युक्त प्रश्नों के उत्तर द्वारा गतिविज्ञान में जड़त्व आघूर्ण (Moment of Inertia in Dynamics),जड़त्व आघूर्ण (Moment of Inertia) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Moment of Inertia in Dynamics
गतिविज्ञान में जड़त्व आघूर्ण
(Moment of Inertia in Dynamics)
Moment of Inertia in Dynamics
गतिविज्ञान में जड़त्व आघूर्ण (Moment of Inertia in Dynamics) के इस आर्टिकल में किसी
कण अथवा ठोस पिण्ड का किसी रेखा के परितः जड़त्व आघूर्ण ज्ञात करना सीखेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.