Models in Mathematics
1.गणित में मॉडल (Models in Mathematics),गणित शिक्षा में गणितीय मॉडल (Mathematical Models in Mathematics Education):
- गणित में मॉडल्स (Models in Mathematics) छात्र-छात्राओं को वास्तविक व स्थाई ज्ञान प्रदान करने के लिए गणित में मॉडल और प्रत्यक्ष वस्तुओं (Articles) का प्रयोग करना आवश्यक है।प्रत्यक्ष वस्तुओं और मॉडल्स को देखकर छात्र-छात्राओं को उससे संबंधित ज्ञान तत्काल और ठीक से समझ में आ जाता है। उदाहरणार्थ गोले (Sphere),अर्धगोले (Hemisphere),शंकु (Cone),बेलन (Cylinder),घनाभ (Cuboid),घन (Cube) इत्यादि ठोस वस्तुओं अथवा उनके मॉडल्स को देखने पर इनका आयतन (Volume),पृष्ठीय क्षेत्रफल (Surface Area),वक्र पृष्ठ का क्षेत्रफल (Curved Surface Area),आधार का क्षेत्रफल (Area of Base) को छात्र-छात्राएं ठीक से समझ लेते हैं।छात्र छात्राओं को त्रिविमीय (Three Dimensional) वस्तुओं को काल्पनिक रूप से समझाना अर्थात् इनके आयतन,क्षेत्रफल इत्यादि को समझाना बहुत कठिन होता है।परंतु जब छात्र-छात्राएं प्रत्यक्ष रूप से इन वस्तुओं को देखकर सवालों को हल करते हैं तो शीघ्रता से उनके बारे में जान-समझ लेते हैं।एक प्रकार से प्रत्यक्ष वस्तुओं को दिखाकर सवालों को हल करना प्रायोगिक (प्रैक्टिकल) कार्य है।और जब प्रैक्टिकल कार्य अर्थात् क्रियात्मक रूप से किसी कार्य को हम करते हैं तो उसको बड़ी आसानी से समझ लेते हैं।
त्रिभुजों के विभिन्न प्रकार समबाहु त्रिभुज (Equilateral Triangle),समकोण त्रिभुज (Right Angled Triangle),समद्विबाहु त्रिभुज (Isosceles Triangle),विषमबाहु त्रिभुज (Scalene Triangle) के मॉडल्स दिखाकर पाइथागोरस प्रमेय तथा विभिन्न साध्यों,प्रमेयों एवं कोणों को समझाया जा सकता है। - हालांकि सभी वस्तुओं को प्रत्यक्ष दिखाना सदैव संभव नहीं होता है।जैसे मीनार की ऊंचाई ज्ञात करने के लिए छात्र-छात्राओं को मीनार तक ले जाना समय नष्ट करना है तथा इससे कई प्रकार की कठिनाइयां उपस्थित होती है।जिन वस्तुओं को प्रत्यक्ष दिखाना संभव नहीं है उनके मॉडल्स का प्रयोग करके उससे संबंधित प्रमेयों,सवालों तथा समस्याओं को समझाया जा सकता है।शिक्षा संस्थान से बाहर ले जाना तथा वस्तुओं को दिखाना न तो व्यावहारिक है और समय भी काफी लगता है। इसलिए शिक्षा संस्थान से बाहर ले जाना कभी-कभी ही संभव होता है।
- कई वस्तुएं तो ऐसी है या ऐसे कार्य हैं जिन्हें दिखाना भी असंभव है जैसे पृथ्वी के चारों ओर चंद्रमा के चक्कर लगाने को प्रत्यक्ष रुप से दिखाना असंभव है फिर भी इनके मॉडल्स का प्रयोग करके ऐसे टॉपिक को समझाया जा सकता है।
- गणित अमूर्त (Abstract) विषय है।संकेतों (Notations),प्रतीकों (Symbols) तथा चिन्हों (signs) का विषय है।ऐसे विषय को मॉडल्स का प्रयोग करके वास्तविकता तथा यथार्थता का पुट दिया जा सकता है।मॉडल्स मूलवस्तु से रूप,रचना,रंग आदि से पूर्णतः मिलते हैं।यदि ऐसे मॉडलों का निर्माण जिनके भागों को अलग कर फिर जोड़ा जा सके तो उनकी उपयोगिता ओर भी बढ़ जाती है।
- मॉडल्स के निर्माण में कागज,लकड़ी का गत्ता,लोहे की पतली छड़ें,मिट्टी,रबर,प्लास्टिक इत्यादि का प्रयोग होता है।यदि इनका निर्माण छात्र-छात्राओं की सहायता से किया जाए तो उनमें रचनात्मकता की प्रवृत्ति का भी विकास होगा।
- ज्यामिति के प्रेमियों को हम तर्क द्वारा सिद्ध करते हैं।यदि इन प्रेमियों की सत्यता मॉडलों द्वारा प्रदर्शित की जाए तो छात्र-छात्राएं ज्यामितीय तर्क को आसानी से समझ लेते हैं।उदाहरणार्थ पाइथागोरस के प्रमेय को एक मॉडल के द्वारा प्रभावी ढंग से समझाया जा सकता है।इसी प्रकार \left(a+b\right)^2,\left(a-b\right)^2 इत्यादि सूत्रों (सर्वसमिकाओं) को मॉडलों द्वारा समझाया जाए तो छात्र छात्राओं के मन में किसी भी प्रकार के संशय को दूर किया जा सकता है।लगभग सभी प्रकार के प्रमेयों के मॉडल्स तैयार किए जा सकते हैं।मॉडल्स का प्रयोग करने से वातावरण सजीव,सरस व आकर्षक बनता है।छात्र-छात्राओं की मॉडल्स के प्रयोग से गणित में रुचि बढ़ाई जा सकती है।लेकिन मॉडल्स का प्रयोग करना अध्यापक की कुशलता,अनुभव और योग्यता पर निर्भर करता है।इन मॉडल्स को गणित कक्ष,संग्रहालय,गणित प्रयोगशाला आदि में रखा जा सकता है।
- ज्यामिति में बोर्ड पर चित्र खींचने से वस्तुओं का समतलीय आकार दो आयामों (Two Dimensions) में ही प्रदर्शित किया जा सकता है।जबकि वास्तविक जीवन में हम वस्तुओं को तीन आयामों (Three Dimensions) में ही देखते हैं। मॉडल्स के उपयोग से छात्र-छात्राओं का ध्यान उनके तीन आयामों की ओर खींचा जा सकता है। वस्तुओं का त्रिविमीय स्वरूप मॉडल्स से दिखाया जाना संभव है।
- आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:Some Strange Numbers in Mathematics
(1.)मॉडल्स के प्रयोग में सावधानियां (Precautions in Using Models):
- (i)मॉडल्स की आकृति इतनी बड़ी होनी चाहिए कि कक्षा के सभी छात्र-छात्राओं को स्पष्ट दिखाई दे जाए।
- (ii)जिस कक्ष में मॉडल्स,प्रत्यक्ष वस्तुओं का प्रदर्शन किया जाए वहां उचित प्रकाश एवं छात्र-छात्राओं को बैठने की पर्याप्त व्यवस्था होनी चाहिए।जिससे छात्र-छात्राएं मॉडल्स व प्रत्यक्ष वस्तु को ठीक से देख सकें।
- (iii)मॉडल्स आकर्षक डिजाइन में तथा रुचिकर होने चाहिए।विभिन्न रंगों तथा सामग्री का प्रयोग करके रुचिकर बनाया जा सकता है।
- (iv)एक ही मॉडल्स में विभिन्न आकृतियों का निर्माण नहीं करना चाहिए।
- (v)मॉडल्स में अत्यधिक तथ्यों का प्रयोग नहीं करना चाहिए जिससे छात्र-छात्राएं समझ ही न सके।
- (vi)मॉडल्स के निर्माण में अच्छी क्वालिटी की वस्तुओं तथा पदार्थ का प्रयोग करना चाहिए इसके बिना मॉडल्स आकर्षणहीन तथा अर्थहीन हो जाएंगे।
- (vii)गणित का टाॅपिक पढ़ाते समय मॉडल्स गणित के टॉपिक से संबंधित ही प्रयोग किए जाने चाहिए।
- (viii)मॉडल्स इतने सरल तथा सुस्पष्ट होने चाहिए जिन्हें देखते ही छात्र-छात्राएं आसानी से समझ लें।
(is - (ix)मॉडल्स में विभिन्न रंगों,सामग्री तथा डिजाइन का प्रयोग करके आकर्षक व रुचिकर बनाया जा सकता है।
- (x)मॉडल्स का प्रदर्शन सही प्रकार तथा वैज्ञानिक ढंग से करना चाहिए।
- (xi)मॉडल्स तैयार किया जाए वे हर दृष्टिकोण से अच्छे होने चाहिए,केवल काम चलाऊ प्रकृति के न हो।
- (xii)मॉडल्स मूल वस्तु से स्वरूप,रचना,रंग आदि में पूर्णतः मिलते-जुलते होना चाहिए।
Also Read This Article:Mathematics is Gem of all Scriptures
(2.)गणित में मॉडल्स के उदाहरण (Examples of Models in Mathematics):
- एक लकड़ी का त्रिभुज लो जिसमें PQ,PS तथा MN पर इस प्रकार मोड़ने की संभावना हो कि A,B,C मोड़ने पर O बिंदु पर मिलते हों।O बिंदु पर तीनों कोणों का योग=180°आए।
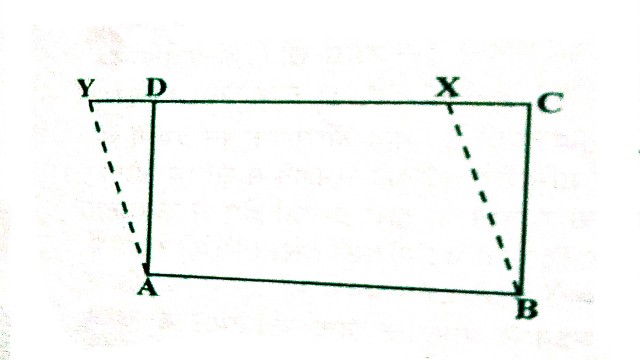
- (ii)आयतो तथा समांतर चतुर्भुज के क्षेत्रफलों संबंधी मॉडल्स जिसमें दोनों के आधार एवं ऊंचाई समान हो तथा जिसमें \triangle AYD,\triangle CXD को परस्पर बदलकर समान क्षेत्रफल को प्रदर्शित किया जा सके।
- (iii)त्रिभुज का मॉडल जिसमें दो रेखाओं के मध्य-बिंदुओं को मिलाने वाली रेखा को नापकर तीसरी की आधी के समान सिद्ध करते हैं।
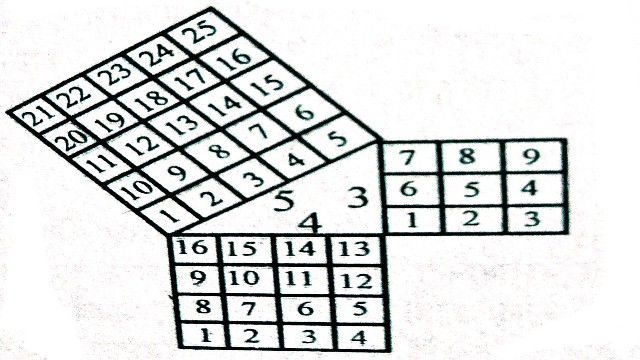
- (iv)पाइथागोरस प्रमेय का मॉडल जिसमें प्रत्यक्ष वर्ग प्रदर्शित किए गए हों तथा कर्ण पर बने वर्गों का योग दोनों भुजाओं पर बने वर्गों के योग के समान हो।
- (v)वृत्तों की स्पर्श रेखाओं को प्रदर्शित करने वाले मॉडल।
- (vi)\left(a+b\right)^3 का एक मॉडल जिसमें वर्ग की भुजा (a+b) इकाई हो तथा उसमें a^2,b^2,ab \text{ तथा }ab की आकृतियां दिखाई देती हों।यह मॉडल लोहे की पतली छड़ों से बनाया जाए।इसी प्रकार \left(a+b\right)^3 का मॉडल बनाया जा सकता है।
- (vii)प्रिज्म (Prism),सिलेंडर (Cylinder),पिरामिड (Pyramid),शंकु, ठोस,गोला आदि मॉडलों द्वारा मेंसुरेशन के सवालों को समझाया जाए।
(3.)सारांश (Conclusion of Models and Articles in Mathematics):
- गणित में रुचि,जिज्ञासा की वृद्धि करने के लिए केवल गणित में अभ्यास कार्य से प्रवीणता व दक्षता प्राप्त नहीं की जा सकती है।क्योंकि बिना जिज्ञासा तथा सद्बुद्धि के रेत में तेल निकालने के समान है। इसलिए गणित में अभ्यास कार्य के साथ-साथ विभिन्न मनोरंजक सामग्रियों,सहायक सामग्री,चित्र,चार्ट,मॉडल्स,प्रत्यक्ष वस्तुओं,गणित क्लब,गणित प्रयोगशाला,गणित लाइब्रेरी,गणित परिषद,पहेलियों,जादुई वर्ग,गणितीय खेल का प्रयोग किया जाए जिससे छात्र-छात्राओं की जिज्ञासा व रुचि में वृद्धि हो।
- उपर्युक्त विवरण में गणित में मॉडल (Models in Mathematics),गणित शिक्षा में गणितीय मॉडल (Mathematical Models in Mathematics Education) के बारे में बताया गया है।
2.गणित में मॉडल और प्रत्यक्ष वस्तुएँ (Models and Articles in Mathematics)
गणित में मॉडल (Models in Mathematics),गणित शिक्षा में गणितीय मॉडल (Mathematical Models in Mathematics Education) के सम्बन्ध में अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.गणित में मॉडल क्या है? (What is Models in Mathematics?):
उत्तर:एक गणितीय मॉडल गणितीय अवधारणाओं और भाषा का उपयोग कर एक प्रणाली का वर्णन है।गणितीय मॉडल विकसित करने की प्रक्रिया को गणितीय मॉडलिंग की संज्ञा दी जाती है।गणितीय मॉडल प्राकृतिक विज्ञान (natural sciences) और इंजीनियरिंग विषयों (engineering disciplines) में उपयोग किया जाता है,साथ ही सामाजिक विज्ञान (social sciences) जैसे गैर-भौतिक प्रणालियों में भी।
प्रश्न:2.गणितीय मॉडल के उदाहरण क्या हैं? (What are examples of mathematical models?):
उत्तर:हालांकि समीकरण और ग्राफ (Graph) गणितीय मॉडल के सबसे आम प्रकार हैं,अन्य प्रकार हैं जो इस श्रेणी में आते हैं।इनमें से कुछ पाई चार्ट (pie charts),टेबल (tables),लाइन ग्राफ (line graphs),रासायनिक सूत्र (chemical formulas) या आरेख (diagrams) शामिल हैं।
प्रश्न:3.क्या गणितीय मॉडल कहा जाता है? (What are called mathematical models?):
उत्तर:प्रतीकात्मक मॉडल (Symbolic Models) को गणितीय मॉडल कहा जाता है।
प्रश्न:4.एक अच्छा गणितीय मॉडल क्या है? (What is a good Mathematical Model?):
उत्तर:एक मॉडल में वस्तुओं या घटनाओं की आवश्यक संरचना होनी चाहिए।
(1.)यह जरूरी अधूरा होना चाहिए।
(2.)इसे सापेक्ष आसानी से बदला या हेरफेर किया जा सकता है (It may be changed or manipulated with relative ease)।
(3.)यह सरलीकरण/आदर्शीकरण है (It is simplification/Idealization)।
प्रश्न:5.गणितीय मॉडल के 5 घटक क्या हैं? (What are the 5 components of a Mathematical Model?):
उत्तर:गणितीय मॉडल के घटक चर (variables) या निर्णय पैरामीटर (decision parameters) हैं;स्थिरांक (constants) और अंशांकन पैरामीटर (calibration);इनपुट पैरामीटर (input parameters),डेटा (data);चरण मापदंड (phase parameters);आउटपुट पैरामीटर (output parameters);शोर और यादृच्छिक मापदंडों (noise and random parameters)।
प्रश्न:6.गणितीय मॉडल क्या है और इसका उद्देश्य क्या है? (What is a mathematical model and what is its purpose?):
उत्तर:गणितीय मॉडलिंग एक आवेदन क्षेत्र से समस्याओं को ट्रैक्ट योग्य गणितीय योगों में अनुवाद करने की कला है जिसका सैद्धांतिक और संख्यात्मक विश्लेषण प्रारंभिक आवेदन के लिए अंतर्दृष्टि (insight),उत्तर (answers) और मार्गदर्शन (guidance) उपयोगी प्रदान करता है।
प्रश्न:7.हम गणितीय मॉडल का उपयोग क्यों करते हैं? (Why do we use mathematical models?):
उत्तर:गणितीय मॉडल छात्रों को समझने और समीकरणों या फलनात्मक संबंधों (functional relationship) के अर्थ का पता लगाने में मदद कर सकते हैं।
एक भौतिक प्रणाली के एक वैचारिक मॉडल को विकसित करने के बाद एक गणितीय मॉडल विकसित करना स्वाभाविक है जो एक प्रणाली के मात्रात्मक व्यवहार का अनुमान लगाने की अनुमति देगा।
प्रश्न:8.गणितीय मॉडलिंग प्रक्रिया के 4 कदम क्या हैं? (What are the 4 steps of the mathematical modeling process?):
उत्तर:इसलिए गणितीय मॉडलिंग में शामिल सूत्रीकरण (formulation),समाधान (solution),व्याख्या (interpretation) और सत्यापन (validation) हैं।
प्रश्न:9.गणित की 7 किस्में क्या हैं? (What are the 7 strands of mathematics?):
उत्तर:गणितीय सामग्री किस्में
संख्या के सन्दर्भ (Number Sense),गुण (properties) और संचालन (operations)।
मापन (Measurement)।
ज्यामिति और स्थानिक सन्दर्भ (Geimetry and Spatial sense)।
डेटा विश्लेषण,आंकड़े और प्रायिकता (Data analysis, statistics and probability)।
बीजगणित और फलन (Algebra and functions)।
उपर्युक्त प्रश्नों के उत्तर द्वारा गणित में मॉडल (Models in Mathematics),गणित शिक्षा में गणितीय मॉडल (Mathematical Models in Mathematics Education) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
Models in Mathematics
गणित में मॉडल (Models in Mathematics)
Models in Mathematics
गणित में मॉडल्स (Models in Mathematics) छात्र-छात्राओं को वास्तविक व स्थाई ज्ञान प्रदान करने के लिए गणित में
मॉडल और प्रत्यक्ष वस्तुओं (Articles) का प्रयोग करना आवश्यक है।प्रत्यक्ष वस्तुओं और
मॉडल्स को देखकर छात्र-छात्राओं को उससे संबंधित ज्ञान तत्काल और ठीक से समझ में आ जाता है।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
