Minima and Maxima Class 12
1.निम्नतम और उच्चतम कक्षा 12 (Minima and Maxima Class 12),अवकलन गणित में उच्चिष्ठ और निम्निष्ठ (Maxima and Minima in Differential Calculus):
निम्नतम और उच्चतम कक्षा 12 (Minima and Maxima Class 12) के इस आर्टिकल की थ्योरी पढ़ने के लिए इससे पूर्व आर्टिकल को पढ़ना चाहिए।इस आर्टिकल में निम्नतम और उच्चतम को कुछ उदाहरणों के द्वारा समझेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Maxima and Minima Class 12
2.निम्नतम और उच्चतम कक्षा 12 पर आधारित उदाहरण (Examples Based on Minima and Maxima Class 12):
Example:4.सिद्ध कीजिए कि निम्नलिखित फलनों का उच्चतम तथा निम्नतम मान नहीं हैः
Example:4(i). f(x)=e^x
Solution: f(x)=e^x \\ f^{\prime}(x)=e^x>0, x \in R
अतः f(x) का मान x के किसी भी मान के लिए सदैव धनात्मक रहता है।
इसलिए फलन का न तो कोई उच्चतम मान है और न निम्नतम मान है।
Example:4(ii). g(x)=\log (x)
Solution: g(x)=\log x, x>0 \\ g^{\prime}(x)=\frac{1}{x}>0, x \in R
(चूँकि g(x)=\log x में x>0 ही रहेगा नहीं तो फलन परिभाषित नहीं होगा)
g'(x) का चिन्ह परिवर्तित नहीं होता है।
क्योंकि जैसे-जैसे x का मान बढ़ेगा g(x) का मान घटेगा तथा जैसे-जैसे x का मान घटेगा g(x) का मान बढ़ेगा।दोनों ही परिस्थितियों में g'(x)>0 रहेगा।
अतः फलन का कोई न तो उच्चतम मान है और न ही न्यूनतम मान है।
Example:4(iii). h(x)=x^3+x^2+x+1
Solution: h(x)=x^3+x^2+x+1 \\ h^{\prime}(x)=3 x^2+2 x+1
उच्चतम तथा निम्नतम मान के लिए
h^{\prime}(x)=0 \\ \Rightarrow 3 x^2+2 x+1=100 \\ \Rightarrow x =\frac{-2 \pm \sqrt{(2)^2-4 \times 3 \times 1}}{2 \times 3} \\ =-\frac{-2 \pm \sqrt{4-12}}{6} \\ =\frac{-2 \pm \sqrt{-8}}{6} \\ = \frac{-2 \pm 2 \sqrt{-2}}{6} \\ x=\frac{-1 \pm \sqrt{-2}}{3}
जो कि वास्तविक नहीं है।
\therefore x \in R के लिए h^{\prime}(x) \neq 0
अतः फलन का न तो उच्चतम मान है और न निम्नतम मान है।
Example:5.प्रदत्त अन्तरालों में निम्नलिखित फलनों के निरपेक्ष उच्चतम मान और निरपेक्ष निम्नतम मान ज्ञात कीजिए।
Example:5(i). f(x)=x^3, x \in [-2,2]
Solution: f(x)=x^{3} \\ f^{\prime}(x)=3 x^2 \\ f^{\prime}(x)=0 \text { से : } \quad 3 x^2=0 \Rightarrow x=0 \\ f(-2)=(-2)^3=-8 \\ f(0)=(0)^3=0 \\ f(2)=(2)^3=8
निरपेक्ष निम्नतम मान=-8
निरपेक्ष उच्चतम मान=8
Example:5(ii). f(x)=\sin x+\cos x, x \in[0, \pi ]
Solution: f(x)=\sin x+\cos x \\ f^{\prime}(x)= \cos x-\sin x \\ \Rightarrow f^{\prime}(x)=0 \text { से : } \\ \cos x-\sin x=0 \\ \tan x=1 \\ \Rightarrow \tan x=\tan \frac{\pi}{4} \Rightarrow x=\frac{\pi}{4} \\ f(0)= \sin 0+\cos 0=1 \\ \Rightarrow f\left( \frac{\pi}{4} \right)=\sin \left( \frac{\pi}{4} \right)+\cos \left( \frac{\pi}{4} \right) \\ =\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}} \\ \Rightarrow f\left(\frac{\pi}{4} \right) =\frac{2}{\sqrt{2}}=\sqrt{2} \\ \Rightarrow f(\pi) =\sin \pi+\cos \pi \\ =0-1 \\ \Rightarrow f(\pi)=-1
फलन का निरपेक्ष उच्चतम मान=\sqrt{2}
फलन का निरपेक्ष निम्नतम मान=-1
Example:5(iii). f(x)=4 x-\frac{1}{2} x^2, x \in\left[-2, \frac{9}{2}\right]
Solution: f(x)=4 x-\frac{1}{2} x^2 \\ f^{\prime}(x) =4-x \\ f^{\prime}(x) =0 \text { से : } \quad 4-x=0 \Rightarrow x=4 \\ f(-2)=4(-2)-\frac{1}{2}(-2)^2 \\ =-8-2 \\ \Rightarrow f(-2) =-10 \\ f(4) =4(4)-\frac{1}{2}(4)^2 \\ \Rightarrow f(4) =16-8=8 \\ f\left(\frac{9}{2}\right) =4 \times \frac{9}{2}-\frac{1}{2}\left(\frac{9}{2}\right)^2 \\ =18-\frac{81}{8} \\ =\frac{144-81}{8} \\ \Rightarrow f\left(\frac{9}{2}\right) =\frac{63}{8}
अतः फलन का निरपेक्ष उच्चतम मान=8
फलन का निरपेक्ष निम्नतम मान=-10
Example:5(iv). f(x)=(x-1)^2+3, x \in \left[-3,1\right]
Solution: f(x)=(x-1)^2+3 \\ f^{\prime}(x)=2(x-1) \\ f^{\prime}(x)=0 \text { से: } \quad 2(x-1)=0 \Rightarrow x=1 \\ f(-3)=(-3-1)^2+3=16+3=19 \\ f(1)=(1-1)^2+3=3
अतः फलन का निरपेक्ष उच्चतम मान=19
फलन का निरपेक्ष निम्नतम मान=3
Example:6.यदि लाभ फलन p(x)=41-72 x-18 x^2 से प्रदत्त है तो किसी कम्पनी द्वारा अर्जित उच्चतम लाभ ज्ञात कीजिए।
Solution: p(x)=41-72 x-18 x^2 \\ p^{\prime}(x)=-72-36 x \ldots(1) \\ p^{\prime}(x)=0 \text { से : } \\ -72-36 x=0 \Rightarrow x=-2
समीकरण (1) का पुनः अवकलन करने पर :
p^{\prime \prime}(x)=-36<0
अतः कम्पनी का लाभ उच्चतम है।
x=2 पर कम्पनी का उच्चतम लाभ
P(x)=41-72 x-18 x^2 \\ P(2)=41-72 \times-2-18(2)^2 \\ =41+144-72 \\ \Rightarrow P(2) =113 इकाई
Example:7.अन्तराल [0,3] पर 3 x^4-8 x^3+12 x^2-48 x+25 के उच्चतम और निम्नतम मान ज्ञात कीजिए।
Solution: y=3 x^4-8 x^3+12 x^2-48 x+25
x के सापेक्ष अवकलन करने परः
\frac{d y}{d x}=12 x^3-24 x^2+24 x-48 \\ \frac{d y}{d x}=0 \text { से : } \quad 12 x^3-24 x^2+24 x-48=0 \\ \Rightarrow 12\left(x^3-2 x^2+2 x-4\right)=0 \\ \Rightarrow x^3-2 x^2+2 x-4=0 \\ \Rightarrow x^2(x-2)+2(x-2)=0 \\ \Rightarrow(x-2)\left(x^2+2\right)=0 \\ \Rightarrow x=2, x=\pm \sqrt{-2} \\ x=\pm \sqrt{-2} सम्भव नहीं है क्योंकि यह वास्तविक संख्या नहीं है।
y(0)=3(0)^4-8(0)^3+12(0)^2-48(0)+25 \\ y(0)=25 \\ y(2)=3(2)^4-8(2)^3+12(2)^2-48 \times 2+25 \\ =48-64+48-96+25 \\ \Rightarrow y(2) =-39 \\ y(3) =3(3)^4-8(3)^3+12(3)^2-48(3)+25 \\ =3 \times 81-8 \times 27+12 \times 9-144+25 \\ =243-216+108-144+25 \\ \Rightarrow y(3) =16
अतः फलन का निरपेक्ष उच्चतम मान (x=0 पर)=25
फलन का निरपेक्ष निम्नतम मान (x=2 पर)=-39
Example:8.अन्तराल [0,2π] के किन बिन्दुओं पर फलन sin 2x अपना उच्चतम मान प्राप्त करता है?
Solution:y=sin 2x
x के सापेक्ष अवकलन करने परः
\frac{d y}{d x}=2 \cos 2 x \\ \frac{d y}{d x}=0 \text { से : } \quad 2 \cos 2 x=0 \\ \cos 2 x=\cos \frac{\pi}{2}, \cos \frac{3 \pi}{2}, \cos \frac{5 \pi}{2}, \cos \frac{7 \pi}{2} \\ \Rightarrow 2 x=\frac{\pi}{2}, \frac{3 \pi}{2}, \frac{5 \pi}{2}, \frac{7 \pi}{2} \\ \Rightarrow x=\frac{\pi}{4}, \frac{3 \pi}{4}, \frac{5 \pi}{4}, \frac{7 \pi}{4}
x=0 तो y(0)=\sin (2 \times 0)=0 \\ x=\frac{2 \pi}{4} तो y(\frac{\pi}{4})=\sin \frac{2 \pi}{4}=1 \\ x=\frac{3 \pi}{4} तो y\left(\frac{3 \pi}{4}\right)=\sin \left(\frac{2 \times 3 \pi}{4}\right)=\sin \left(\frac{3 \pi}{2}\right)=-1 \\ x=\frac{5 \pi}{4} तो y\left(\frac{5 \pi}{4}\right)=\sin \left(2 \times \frac{5 \pi}{4}\right)=\sin \left(\frac{5 \pi}{2}\right)=1 \\ x=\frac{7 \pi}{4} तो y\left(\frac{7 \pi}{4}\right)=\sin \left(\frac{2 \times 7 \pi}{4}\right)=\sin \left(\frac{7 \pi}{2}\right)=-1 \\ x=2 \pi तो y(2 \pi)=\sin (2 \times 2 \pi)=\sin 4 \pi=0
अतः फलन x=\frac{\pi}{4} व x=\frac{5 \pi}{4} पर उच्चतम मान प्राप्त करता है=1
Example:9.फलन sin x+cos x का उच्चतम मान क्या है?
Solution: y=\sin x + \cos x
x के सापेक्ष अवकलन करने परः
\frac{d y}{d x}=\cos x-\sin x \\ \frac{d y}{d x}=0 \text { से : }=\cos x-\sin x=0 \\ \Rightarrow \tan x=1 \\ \Rightarrow \tan x=\tan \frac{\pi}{4}, \tan \frac{5 \pi}{4} \\ \Rightarrow x=\frac{\pi}{4},\frac{5 \pi}{4}
x=0 तो y(0)=\sin 0+\cos 0=1 \\ x=\frac{\pi}{4} तो y(\frac{\pi}{4})=\sin \frac{\pi}{4}+\cos \frac{\pi}{4}=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=\sqrt{2} \\ x=\frac{5 \pi}{4} तो y\left(\frac{5 \pi}{4}\right)=\sin \left(\frac{5 \pi}{4}\right)+\cos \left(\frac{5 \pi}{4}\right) \\ \Rightarrow y\left(\frac{5 \pi}{4}\right)=-\cos \frac{\pi}{4}-\cos \frac{\pi}{4}=-\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}=-\sqrt{2} \\ x=2 \pi तो y(2 \pi)=\sin 2 \pi+\cos 2 \pi=1
अतः फलन का उच्चतम मान (x= \frac{\pi}{4} पर)=\sqrt{2}
Example:10.अन्तराल [1,3] में 2x^3-24 x+107 का महत्तम मान ज्ञात कीजिए।इसी फलन का अन्तराल [-3,-1] में भी महत्तम मान ज्ञात कीजिए।
Solution: y=2 x^3-24 x+107
x के सापेक्ष अवकलन करने परः
\frac{d y}{d x}=6 x^2-24 \\ \frac{d y}{d x}=0 \text { सेः } 6 x^2-24=0 \Rightarrow x=\pm 2 \\ -2 \notin [1,3] \\ \therefore x=2 क्योंकि 2 \in [1,3]
जब x=1 तो y(1)=2(1)^3-24(1)+107 \\ \Rightarrow y(1)=2-24+107=85
जब x=2 तो y(2)=2(2)^3-24 \times 2+107 \\ =16-48+107 \\ \Rightarrow y(2)=75
जब x=3 तो y(3)=2(3)^3-24 \times 3+107 \\ =54-72+107 \\ \Rightarrow y(3)=89
अतः अन्तराल [1,3] में x=2 पर फलन का उच्चतम मान=89
अब अन्तराल [-3,-1] के लिए
x=-1,-2,-3
x=-1 तो y(-1)=2(-1)^3-24 x-1+107 \\ =-2+24+107 \\ \Rightarrow y(1)=129
x=-2 तो y(-3)=2(-3)^3-24 x-3+107 \\ =-54+72+107 \\\Rightarrow y(-3)=125
अतः अन्तराल [-3,-1] में फलन का उच्चतम मान (x=-2 पर)=139
Example:11.यदि दिया हुआ है कि अन्तराल [0,2] में x=1 पर फलन x^4-62 x^2+a x+9 उच्चतम मान प्राप्त करता है,तो a का मान ज्ञात कीजिए।
Solution: y=x^4-62 x^2+a x+9
x के सापेक्ष अवकलन करने परः
\frac{d y}{d x}=4 x^3-124 x+a \ldots(1)
x=1 पर \frac{d y}{d x}=0 \\ 4(1)^3-124(-1)+a=0 \Rightarrow a=120
समीकरण (1) का पुनः x के सापेक्ष अवकलन करने परः
\frac{d^2 y}{d x^2}=12 x^2-124 \\ \left(\frac{d^2 y}{d x^2}\right)_{(x=1)}=12(1)^2-124=-112<0
अतः x=1 पर फलन उच्चतम है जब a=120
Example:12. [0,2π] पर x+sin 2x का उच्चतम और निम्नतम मान ज्ञात कीजिए।
Solution: y=x+\sin 2 x
x के सापेक्ष अवकलन करने परः
\frac{d y}{d x}=1+2 \cos 2 x \\ \frac{d y}{d x}=0 \text { से : } \\ 1+2 \cos 2 x=0 \Rightarrow \cos 2 x=-\frac{1}{2} \\ \Rightarrow \cos 2 x=\cos \frac{2 \pi}{3}, \cos \frac{4 \pi}{3}, \cos \frac{8 \pi}{3}, \cos \frac{10 \pi}{3} \\ \Rightarrow 2 x=\frac{2 \pi}{3}, \frac{4 \pi}{3}, \frac{8 \pi}{3}, \frac{10 \pi}{3} \\ \Rightarrow x=\frac{\pi}{3}, \frac{2 \pi}{3}, \frac{4 \pi}{3}, \frac{5 \pi}{3}
x=0 तो y(0)=0+\sin (2 \times 0)=0 \\ x=\frac{\pi}{3} तो y(\frac{\pi}{3})=\frac{\pi}{3}+\sin \frac{2 \pi}{3}=\frac{\pi}{3}+\frac{\sqrt{3}}{2} \\ x=\frac{2 \pi}{3} तो y\left(\frac{2 \pi}{3}\right)=\frac{2 \pi}{3}+\sin \frac{4 \pi}{3}=\frac{2 \pi}{3}-\frac{\sqrt{3}}{2} \\ x=\frac{4 \pi}{3} तो y\left(\frac{4 \pi}{3}\right)=\frac{4 \pi}{3}+\sin \left(\frac{8 \pi}{3}\right)=\frac{4 \pi}{3}+\frac{\sqrt{3}}{2} \\ x=\frac{5 \pi}{3} तो y\left(\frac{5 \pi}{3}\right)=\frac{5 \pi}{3}+\sin \left(\frac{5 \pi}{3}\right)=\frac{5 \pi}{3}-\frac{\sqrt{3}}{2} \\ x=2 \pi तो y(2 \pi)=2 \pi+\sin 2 \pi=2 \pi
इसलिए फलन का उच्चतम मान (x=2π पर)=2π
फलन का निम्नतम मान (x=0 पर)=0
Example:13.ऐसी दो संख्याएँ ज्ञात कीजिए जिनका योग 24 है और जिनका गुणनफल उच्चतम हो।
Solution:माना संख्याएँ=x,24-x
प्रश्नानुसारः y=x(24-x) \\ \Rightarrow y=24 x-x^2 \ldots(1)
x के सापेक्ष अवकलन करने परः
\frac{d y}{d x}=24-2 x \\ \frac{d y}{d x}=0 \text { से: } \quad 24-2 x=0 \Rightarrow x=12
समीकरण (1) का पुनः x के सापेक्ष अवकलन करने परः
\frac{d^2 y}{d x^2}=-2<0
अतः फलन उच्चतम है जब x=12
दूसरी संख्या=24-x=24-12=12
अतः दोनों संख्याएँ=12,12
Example:14.ऐसी दो धन संख्याएँ x और y ज्ञात कीजिए ताकि x+y=60 और उच्चतम हो।
Solution: x+y=60 \Rightarrow y=60-x
माना f(x)=x y^3 \\ \Rightarrow f(x)=x(60-x)^3
x के सापेक्ष अवकलन करने परः
f^{\prime}(x)=(60-x)^3+x \cdot 3(60-x)^2(-1) \\ \Rightarrow f^{\prime}(x)=(60-x)^2(60-x-3 x) \\ \Rightarrow f^{\prime}(x)=(60-x)^2(60-4 x) \ldots(1) \\ f^{\prime}(x)=0 \text { से: } \\ (60-x)^2(60-4 x)=0 \\ \Rightarrow x=60,15
x=60 (असम्भव है) अतः x=15
पुनः समीकरण (1) का x के सापेक्ष अवकलन करने परः
f^{\prime \prime}(x) =2(60-x)(-1)(60-4 x)+(60-x)(-4) \\ =2(60-x)(-60+4 x-120+2 x) \\ =2(60-x)(6 x-180) \\ \Rightarrow f^{\prime \prime}(x) =12(60-x)(x-30) \\ f^{\prime \prime}(15)=12(60-15)(15-30) \\ =12 \times 45 \times-15 \\ \Rightarrow f^{\prime \prime}(x)=-8100<0
अतः f(x) महत्तम है जब x=15
Example:15.ऐसी दो संख्याएँ x और y ज्ञात कीजिए जिनका योग 35 हो और गुणनफल x^2 y^5 उच्चतम हो।
Solution:प्रश्नानुसार x+y=35
\Rightarrow y=35-x
माना P(x)=x^2 y^5 \\ \Rightarrow P(x)=x^2(35-x)^5
x के सापेक्ष अवकलन करने परः
\frac{d p}{d x}=2 x(35-x)^5+x^2 \cdot 5(35-x)^4(-1) \\ =(35-x)^4\left[2 x(35-x)-5 x^2\right] \\ =x(35-x)^4(70-2 x-5 x) \\ \Rightarrow \frac{d p}{d x}=x(35-x)^4(70-7 x) \\ \Rightarrow \frac{d p}{d x}=7 x(35-x)^4(10-x) \ldots(1) \\ \frac{d p}{d x}=0 \text { से: } \\ 7 x(35-x)^4(10-x)=0 \\ \Rightarrow x=0,35,10
x=0,35,10
x=0,35 असम्भव हैं।अतः x=10
समीकरण (1) का पुनः x के सापेक्ष अवकलन करने परः
\frac{d^2 p}{d x^2}= 7(35-x)^4(10-x)+7 x \times 4(35-x)^3(-1)(10-x)+7 x(35-x)^4(-1) \\ =7(35-x)^3[(35-x)(10-x)-4 x(10-x)-x(35-x)] \\=7(35-x)^3\left[3 x^2-120 x+350\right] \\ \Rightarrow \frac{d^2 p}{d x^2} =14(35-x)^3\left(3 x^2-60 x+175\right) \\ \Rightarrow\left(\frac{d^2 p}{d x^2} \right)_{(x=10)} =14(35-10)^3\left[3 \times 10^2-60 \times 10+175\right] \\ =14 \times 25^3(300-600+175) \\ =14 \times 5625 \times(-125) \\ \Rightarrow \left(\frac{d^2 p}{d x^2}\right)_{(x=10)}=-27343750<0
अतः p(x) उच्चतम है जब x=10
y=35-x=35-10=25
x=10,y=25
Example:16.ऐसी दो धन संख्याएँ ज्ञात कीजिए जिनका योग 16 हो और जिनके घनों का योग न्यूनतम हो।
Solution:माना दो धन संख्याएँ=x,16-x
तथा y=x^3+(16-x)^3
x के सापेक्ष अवकलन करने परः
\frac{d y}{d x}=3 x^2+3(16-x)^2(-1) \\ \Rightarrow \frac{d y}{d x}=3\left(x^2-x^2+32 x-256\right) \\ \Rightarrow \frac{d y}{d x}=96(x-8) \ldots(1) \\ \frac{d y}{d x}=0 \text { से : } \\ 96(x-8)=0 \Rightarrow x=8
समीकरण (1) का पुनः x के सापेक्ष अवकलन करने परः
\frac{d^2 y}{d x^2}=96>0
अतः y निम्नतम होगा जब x=8
अतः संख्याएँ x=8,16-x=16-8=8
संख्याएँ=8,8
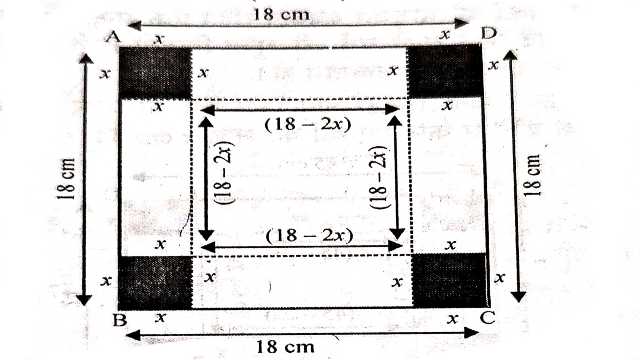
Example:17.18 cm भुजा के टिन के किसी वर्गाकार टुकड़े से प्रत्येक कोने पर एक वर्ग काटकर तथा इस प्रकार बनें टिन के फलकों को मोड़कर ढक्कन रहित एक बन्दूक बनाना है।काटे जाने वाले वर्ग की भुजा कितनी होगी जिससे सन्दूक का आयतन उच्चतम हो?
Solution:माना ABCD टिन का वर्गाकार टुकड़ा है जिसकी भुजा 18 cm है।
पुनः माना प्रत्येक कोने से x सेमी भुजा का वर्ग टिन से काटकर निकाला गया है।
अतः टिन से बने सन्दूक की लम्बाई (l)=18-2x सेमी
चौड़ाई (b)=18-2x सेमी
तथा ऊँचाई (h)=x सेमी
सन्दूक का आयतन V=l×b×h
\Rightarrow V=(18-2 x)(18-2 x) x \\ \Rightarrow V=x(18-2 x)^2
x के सापेक्ष अवकलन करने परः
\frac{d V}{d x} =1 \cdot(18-2 x)^2+2(18-2 x) \cdot(-2) x \\ =(18-2 x)(18-2 x-4 x) \\ =(18-2 x)(18-6 x) \\ \Rightarrow \frac{d V}{d x}=12(9-x)(3-x) \cdots(1) \\ \frac{d V}{d x} =0 \text { से : } \\ 12(9-x)(3-x)=0 \\ \Rightarrow x=9,3 \\ x \neq 9 अतः x=3
समीकरण (1) का पुनः x के सापेक्ष अवकलन करने परः
\frac{d^2 V}{d x^2} =12(9-x)(-1)+12(3-x)(-1) \\ =-12(9-x+3-x) \\ =-12(12-2 x) \\ \left(\frac{d^{2} V}{d x^2}\right) =-24(6-x)\\ \left(\frac{d^{2} V}{d x^2}\right)_{(x=3)}=-24(6-3)=-72<0
अतः x=3 पर आयतन उच्चतम है।
फलतः काटे जाने वाले वर्ग की भुजा 3 सेमी होगी।
उपर्युक्त उदाहरणों के द्वारा निम्नतम और उच्चतम कक्षा 12 (Minima and Maxima Class 12),अवकलन गणित में उच्चिष्ठ और निम्निष्ठ (Maxima and Minima in Differential Calculus) को समझ सकते हैं।
3.निम्नतम और उच्चतम कक्षा 12 पर आधारित सवाल (Questions Based on Minima and Maxima Class 12):
(1.)सिद्ध कीजिए कि किसी वृत्त में बड़े से बड़ा त्रिभुज जो खींचा जा सकता है,वह समबाहु होगा।
(2.)सिद्ध कीजिए की दी हुई तिर्यक ऊँचाई और अधिकतम आयतन वाले शंकु का अर्धशीर्ष कोण \tan^{-1}(\sqrt{2}) है।
उपर्युक्त सवालों को हल करने पर निम्नतम और उच्चतम कक्षा 12 (Minima and Maxima Class 12),अवकलन गणित में उच्चिष्ठ और निम्निष्ठ (Maxima and Minima in Differential Calculus) को समझ सकते हैं।
Also Read This Article:-Approximation in Class 12
4.निम्नतम और उच्चतम कक्षा 12 (Frequently Asked Questions Related to Minima and Maxima Class 12),अवकलन गणित में उच्चिष्ठ और निम्निष्ठ (Maxima and Minima in Differential Calculus) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्नः
प्रश्न:1.क्रान्तिक बिन्दु किसे कहते हैं?(What is Critical Point Called?):
उत्तरःफलन f के प्रान्त में यदि कोई बिन्दु इस प्रकार हो कि इसके लिए f'(c)=0 या बिन्दु c पर फलन अवकलनीय न हो तो बिन्दु c को फलन का क्रान्तिक बिन्दु या स्थिर बिन्दु (stationary point) कहते हैं।
पुनः यदि फलन f बिन्दु c पर सतत हो तथा f'(c)=0 तो h>0 का अस्तित्व इस प्रकार है कि अन्तराल (c-h,c+h) में फलन f अवकलनीय है।
प्रश्न:2.स्थानीय उच्चतम मान और स्थानीय निम्नतम मान से क्या तात्पर्य है? (What do You Mean by Local Maximum Value and Local Minimum Value?):
उत्तरःयदि c फलन f का एक स्थानीय उच्चतम बिन्दु है तो f(c) फलन f का स्थानीय उच्चतम मान है।इसी प्रकार यदि c फलन f का स्थानीय निम्नतम बिन्दु है तो f(c) फलन f का स्थानीय निम्नतम मान है।
प्रश्न:3.स्थानीय उच्चतम और स्थानीय निम्नतम बिन्दु कब नहीं होता है? (When is the Local Maximum and Local Minimum Point not There?):
उत्तरःयदि c के बायीं ओर से दायीं ओर जाने पर अर्थात् f'(x) का चिन्ह अन्तराल R में कभी भी नहीं बदलता है।अतः f के आलेख में कोई भी वर्तन बिन्दु (Turning Points) नहीं है और इसलिए स्थानीय उच्चतम या स्थानीय निम्नतम का कोई बिन्दु नहीं है।
प्रश्न:4.नति परिवर्तन बिन्दु किसे कहते हैं? (What is Point of Inflexion?):
उत्तरःयदि x=c पर फलन f(x) के लिए f'(c)=o,f”(c)=0 परन्तु f^{\prime \prime \prime}(c) \neq 0 तो यह बिन्दु नति परिवर्तन बिन्दु (point of inflexion) कहलाता है।
उपर्युक्त प्रश्नों के उत्तर द्वारा निम्नतम और उच्चतम कक्षा 12 (Minima and Maxima Class 12),अवकलन गणित में उच्चिष्ठ और निम्निष्ठ (Maxima and Minima in Differential Calculus) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Minima and Maxima Class 12
निम्नतम और उच्चतम कक्षा 12
(Minima and Maxima Class 12)
Minima and Maxima Class 12
निम्नतम और उच्चतम कक्षा 12 (Minima and Maxima Class 12) के इस आर्टिकल
की थ्योरी पढ़ने के लिए इससे पूर्व आर्टिकल को पढ़ना चाहिए।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.