Mid-Point Theorem Class 9
1.मध्य-बिन्दु प्रमेय कक्षा 9 (Mid-Point Theorem Class 9),मध्य-बिन्दु प्रमेय (Mid-Point Theorem):
मध्य-बिन्दु प्रमेय कक्षा 9 (Mid-Point Theorem Class 9) एक त्रिभुज की भुजाओं के मध्य बिन्दुओं से सम्बन्धित है।इस आर्टिकल में मध्य-बिन्दु प्रमेय और इस पर आधारित उदाहरणों का अध्ययन करेंगे।
प्रमेय (Theorem):8.9.किसी त्रिभुज की किन्हीं दो भुजाओं के मध्य-बिन्दुओं को मिलानेवाला रेखाखण्ड तीसरी भुजा के समान्तर होता है।
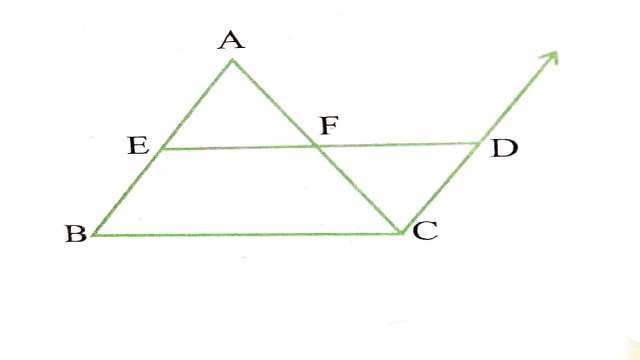
दिया है (Given): \triangle ABC में बिन्दु E और F क्रमशः भुजाओं AB और AC के मध्य-बिन्दु हैं।
सिद्ध करना है (To Prove):(i) EF \| B C (ii) E F=\frac{1}{2} B G
रचना (Construction): CD \| B A खींची तथा DF को D तक बढ़ाया।
उपपत्ति (Proof): \triangle AEF तथा \triangle CDF में
\angle EAF=\angle DCF (एकान्तर कोण)
AF=FC (दिया है)
\angle AFE=\angle CFD (शीर्षाभिमुख कोण)
ASA सर्वांगसमता गुणधर्म से
\triangle AEF \cong \triangle CDF
EF=DF तथा BE=AE=DC (CPCT से)
चतुर्भुज BCDE में
BC=DE तथा B E \| C D
अतः BCDE समान्तर चतुर्भुज है।
\therefore E F \| B C
परन्तु EF=\frac{1}{2} E D=\frac{1}{2} B C \\ \Rightarrow E F=\frac{1}{2} B C
प्रमेय (Theorem):8.10.किसी त्रिभुज की एक भुजा के मध्य-बिन्दु से दूसरी भुजा के समान्तर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है।
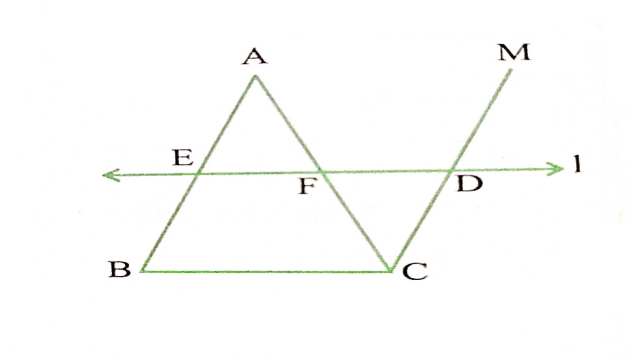
दिया है (Given): \triangle ABC में AE=EB तथा EF \| B C
सिद्ध करना है (To Prove):AF=FC
रचना (Construction): BA \| CM रेखा खींची।EF को D तक बढ़ाया।
उपपत्ति (Proof):चतुर्भुज BCDE में
BC \| ED (दिया है)
BE \| CD (रचना से)
अतः BCDE समान्तर चतुर्भुज है।
अतः BE=CD (CPCT से)
परन्तु AE=BE (दिया है)
अतः AE=CD=BE
\triangle AEF तथा \triangle CDF में
AE=CD (सिद्ध किया है)
\angle EAF=\angle DCF (एकान्तर कोण)
\angle AEF=\angle CDF (एकान्तर कोण)
ASA सर्वांगसमता गुणधर्म से
\triangle AEF \cong \triangle CDF
AF=FC (CPCT से)
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Quadrilaterals Class 9
2.मध्य-बिन्दु प्रमेय कक्षा 9 पर आधारित उदाहरण (Examples Based on Mid-Point Theorem Class 9):
Example:1.ABCD एक चतुर्भुज है जिसमें P,Q,R और S क्रमशः भुजाओं AB,BC,CD और DA के मध्य-बिन्दु हैं (देखिए आकृति)।AC उसका एक विकर्ण है।दर्शाइए कि
(i) SR \| AC और SR=\frac{1}{2} AC है।
(ii)PQ=SR है।
(iii) PQRS एक समान्तर चतुर्भुज है।
Solution:दिया है (Given):ABCD एक चतुर्भुज है जिसमें P,Q,R और S क्रमशः भुजाओं AB,BC,CD और DA के मध्य-बिन्दु हैं।AC उसका एक विकर्ण है।
सिद्ध करना है (To Prove):(i) SR \| AC और SR=\frac{1}{2} AC है।
(ii)PQ=SR है।
(iii) PQRS एक समान्तर चतुर्भुज है।
उपपत्ति (Proof):(i) \triangle DAC में S और R क्रमशः भुजाओं AD और CD के मध्य-बिन्दु हैं।
S R \| A C और SR=\frac{1}{2} AC (मध्य-बिन्दु प्रमेय से)…. (1)
(ii) \triangle BAC में P और Q क्रमशः भुजाओं AB और BC के मध्य-बिन्दु है।
PQ \| A C तथा PQ=\frac{1}{2} A C (मध्य-बिन्दु प्रमेय से)… (2)
(1) व (2) सेः
PQ=SR
तथा PQ \| SR ……(3)
(iii)चतुर्भुज PQRS में
PQ=SR तथा PQ \| SR
अतः PQRS एक समान्तर चतुर्भुज है।
Example:2.ABCD एक समचतुर्भुज है और P,Q,R और S क्रमशः भुजाओं AB,BC,CD और DA के मध्य-बिन्दु है।दर्शाइए कि चतुर्भुज PQRS एक आयत है।
Solution:दिया है (Given):ABCD एक समचतुर्भुज है।P,Q,R और S क्रमशः भुजाओं AB,BC,CD और DA के मध्य-बिन्दु हैं।
सिद्ध करना है (To Prove):चतुर्भुज PQRS एक आयत है।
रचना (Construction):A और C को मिलाया।
उपपत्ति (Proof): \triangle BAC में P और Q क्रमशः भुजाओं AB और PQ के मध्य-बिन्दु हैं।
अतः PQ=\frac{1}{2} A C और PQ \| A C …..(1)
(मध्य-बिन्दु प्रमेय से)
इसी प्रकार \triangle DAC में S व R क्रमशः भुजाओं AB और PQ के मध्य-बिन्दु हैं।
अतः SR \| A C तथा SR=\frac{1}{2} A C……(2)
(मध्य-बिन्दु प्रमेय से)
(1) व (2) सेः
PQ=SR और PQ \| SR
अतः PQRS एक समान्तर चतुर्भुज है।
SP \| BD और RQ \| BD
तथा AC \perp BD और PQ \perp PS
अतः PQRS एक आयत है।
Example:3.ABCD एक आयत है, जिसमें P,Q,R और S क्रमशः भुजाओं AB,BC,CD और DA के मध्य-बिन्दु हैं।दर्शाइए कि चतुर्भुज PQRS एक समचतुर्भुज है।
Solution:दिया है (Given):ABCD एक आयत है।P,Q,R और S क्रमशः भुजाओं AB,BC,CD और DA के मध्य-बिन्दु हैं।
सिद्ध करना है (To Prove):PQRS एक समचतुर्भुज है।
रचना (Construction):AC और BD को मिलाया।
उपपत्ति (Proof): \triangle ABC में P और Q क्रमशः भुजाओं AB और BC के मध्य-बिन्दु हैं।
PQ \| AC और PQ=\frac{1}{2} A C……(1)
(मध्य-बिन्दु प्रमेय से)
पुनः \triangle ACD में R और S क्रमशः भुजाओं CD और AD के मध्य-बिन्दु हैं।
\therefore SR \| AC और SR=\frac{1}{2} A C…..(2)
(मध्य-बिन्दु प्रमेय से)
(1) व (2) सेः
PQ=SR और PQ \| SR
\therefore PQRS एक समान्तर चतुर्भुज है।
\therefore ABCD एक आयत है।
\therefore AC=BD
\Rightarrow \frac{1}{2} A C=\frac{1}{2} B D
PQ=QR=RS=SP
अतः PQRS एक समचतुर्भुज है।
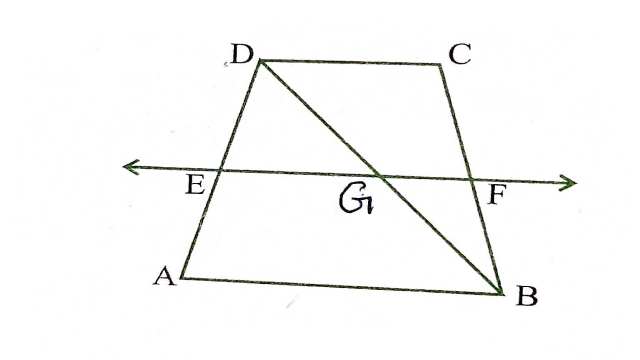
Example:4.ABCD एक समलम्ब है, जिसमें AB \| D C है।साथ ही,BD एक विकर्ण है और E भुजा AD का मध्य-बिन्दु है।E से होकर एक रेखा AB के समान्तर खींची गई है,जो BC को F पर प्रतिच्छेद करती है (देखिए आकृति)।दर्शाइए कि F भुजा BC का मध्य-बिन्दु है।
Solution:दिया है (Given):ABCD एक समलम्ब चतुर्भुज है जिसमें AB \| D C है।BD एक विकर्ण है तथा AD का मध्य-बिन्दु E है।E से होकर AB के समान्तर एक रेखा खींची जो BC को F पर प्रतिच्छेद करती है।
सिद्ध करना है (To Prove):F भुजा BC का मध्य-बिन्दु है।
रचना (Construction):EF, BD को G पर प्रतिच्छेद करती है।
उपपत्ति (Proof): \triangle ABD में
AE=ED तथा EG \| AB
\therefore G,BD का मध्य-बिन्दु है। (मध्य-बिन्दु प्रमेय के विलोम से)
\triangle BCD में
BG=GD (सिद्ध किया है)
तथा GF \| DC [ \because EF \| AB तथा AB \| CD ]
\therefore F,BC का मध्य-बिन्दु है।
Example:5.एक समान्तर चतुर्भुज ABCD में E और F क्रमशः भुजाओं AB और CD के मध्य-बिन्दु हैं (देखिए आकृति)।दर्शाइए कि रेखाखण्ड AF और EC विकर्ण BD को समत्रिभाजित करते हैं।
Solution:दिया है (Given):समान्तर चतुर्भुज ABCD में बिन्दु E और F क्रमशः भुजाओं AB और CD के मध्य-बिन्दु हैं।
सिद्ध करना है (To Prove):DP=PQ=BQ
उपपत्ति (Proof): AE=\frac{1}{2} AB तथा FC=\frac{1}{2} CD \cdots(1)
परन्तु AB \| CD और AB=CD …. (2)
(समान्तर चतुर्भुज की सम्मुख भुजाएँ समान्तर व बराबर होती हैं)
(1) व (2) सेः
AE = FC और AE \| FC
\therefore AECF एक समान्तर चतुर्भुज है।
\triangle DQC में
F, DC का मध्य-बिन्दु है तथा PF \| QC
अतः DP=PQ (मध्य-बिन्दु प्रमेय के विलोम से)… (3)
इसी प्रकार \triangle BAP में
BE=AE तथा EQ \| AP
BQ=PQ …. (4)
(3) व (4) सेः
DP=PQ=BQ
Example:6.दर्शाइए कि किसी चतुर्भुज की सम्मुख भुजाओं के मध्य बिन्दुओं को मिलाने वाले रेखाखण्ड परस्पर समद्विभाजित करते हैं।
Solution:दिया है (Given):एक चतुर्भुज ABCD में बिन्दु P,Q,R और S क्रमशः भुजाओं AB,BC,CD और DA के मध्य-बिन्दु हैं।
सिद्ध करना है (To Prove):SQ और PR एक-दूसरे को समद्विभाजित करते हैं।
उपपत्ति (Proof): \triangle BAC में
BP=AP तथा BQ=CQ
\therefore PQ \| AC और PQ=\frac{1}{2} AC
(मध्य-बिन्दु प्रमेय से)
इसी प्रकार \triangle DAC में
DS=SA तथा DR=RC
\therefore SR \| AC तथा SR=\frac{1}{2} A C ……(2)
(मध्य-बिन्दु प्रमेय से)
(1) व (2) सेः
PQ = SR तथा PQ \| SR
अतः PQRS समान्तर चतुर्भुज है।
परन्तु समान्तर चतुर्भुज के विकर्ण एक-दूसरे को समद्विभाजित करते हैं।अतः
SQ तथा PR एक-दूसरे को समद्विभाजित करते हैं।
Example:7.ABC एक त्रिभुज है जिसका कोण C समकोण है।कर्ण AB के मध्य-बिन्दु M से होकर BC के समान्तर खींची गई रेखा AC को D पर प्रतिच्छेद करती है।दर्शाइए कि
(i)D भुजा AC का मध्य-बिन्दु है।
(ii) MD \perp AC है
(iii) CM=MA=\frac{1}{2} AB है।
Solution:दिया है (Given): \triangle ABC में \angle C=90^{\circ} है।कर्ण AB के मध्य-बिन्दु M से BC के समान्तर रेखाखण्ड खींचा जो AC को D पर प्रतिच्छेद करता है।
सिद्ध करना है (To Prove):(i)D भुजा AC का मध्य-बिन्दु है।
(ii) MD \perp AC है
(iii) CM=MA=\frac{1}{2} AB है।
उपपत्ति (Proof):(i) \triangle ABC में
AM=MB तथा MD \| BC
\therefore D, AC का मध्य-बिन्दु है।(मध्य-बिन्दु प्रमेय के विलोम से)
(ii) BC \| MD तथा AC \perp BC
अतः MD \perp AC
(iii) \triangle ADM और \triangle CDM में
DM=DM (उभयनिष्ठ भुजा)
\angle ADM=\angle CDM=90^{\circ}
AD=DC (सिद्ध किया है)
SAS सर्वांगसमता गुणधर्म से
AM=CM (CPCT से)
परन्तु AM=MB=\frac{1}{2} AB (दिया है)
अतः CM=AM=\frac{1}{2} AB
उपर्युक्त उदाहरणों के द्वारा मध्य-बिन्दु प्रमेय कक्षा 9 (Mid-Point Theorem Class 9),मध्य-बिन्दु प्रमेय (Mid-Point Theorem) को समझ सकते हैं।
3.मध्य-बिन्दु प्रमेय कक्षा 9 पर आधारित सवाल (Questions Based on Mid-Point Theorem Class 9):
(1.)सिद्ध कीजिए कि एक समचतुर्भुज की आसन्न भुजाओं के मध्य बिन्दुओं से बना चतुर्भुज एक आयत होता है।
(2.)आकृति में, \triangle ABC में, AB=AC।बिन्दु D,E,F क्रमशः भुजाओं BC,CA और AB के मध्यबिन्दु हैं।सिद्ध कीजिए कि रेखाखण्ड AD रेखाखण्ड EF पर लम्ब है और इसके द्वारा समद्विभाजित होता है।
उपर्युक्त सवालों को हल करने पर मध्य-बिन्दु प्रमेय कक्षा 9 (Mid-Point Theorem Class 9),मध्य-बिन्दु प्रमेय (Mid-Point Theorem) को ठीक से समझ सकते हैं।
Also Read This Article:-Triangle in Class 9
4.मध्य-बिन्दु प्रमेय कक्षा 9 (Frequently Asked Questions Related to Mid-Point Theorem Class 9),मध्य-बिन्दु प्रमेय (Mid-Point Theorem) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.चतुर्भुज की सम्मुख भुजाओं को परिभाषित करो। (Define the Opposite Sides of the Quadrilateral):
उत्तर:चतुर्भुज की वे भुजाएँ,जिनका कोई उभयनिष्ठ (common) बिन्दु न हो,सम्मुख भुजाएँ कहलाती हैं।
प्रश्न:2.चतुर्भुज की क्रमागत भुजाओं को परिभाषित करो। (Define the Adjacent Sides of a Quadrilateral):
उत्तर:चतुर्भुज की वे भुजाएँ,जिनका एक उभयनिष्ठ अंत्य बिन्दु (end-point) हो,क्रमागत भुजाएँ कहलाती हैं।
प्रश्न:3.चतुर्भुज के क्रमागत कोणों को परिभाषित करो। (Define the Adjacent Angles of the Quadrilateral):
उत्तर:चतुर्भुज के वे दो कोण,जिनको अन्तरित करने वाली भुजाओं में एक भुजा सर्वनिष्ठ हो,क्रमागत (आसन्न) कोण कहलाते हैं।
प्रश्न:4.चतुर्भुज के सम्मुख कोणों की परिभाषा दीजिए।(Define the Opposite Angles of the Quadrilateral):
उत्तर:चतुर्भुज के वे दो कोण, जिनको अन्तरित करनेवाली भुजाओं में से कोई भुजा सर्वनिष्ठ न हो,सम्मुख कोण कहलाते हैं।
प्रश्न:5.चतुर्भुज की मुख्य बातें लिखिए।(Write Down HIGHLIGHTS of the Quadrilateral):
उत्तर:(1.)किसी चतुर्भुज के कोणों का योग 360° होता है।
(2.)समान्तर चतुर्भुज का एक विकर्ण उसे दो सर्वांगसम त्रिभुजों में विभाजित करता है।
(3.)एक समान्तर चतुर्भुज में
(i)सम्मुख भुजाएँ बराबर होती है।
(ii)सम्मुख कोण बराबर होते हैं।
(iii)विकर्ण परस्पर समद्विभाजित करते हैं।
(4.)एक चतुर्भुज समान्तर चतुर्भुज होता है यदि
(i)सम्मुख भुजाएँ बराबर हो; या (ii)सम्मुख कोण बराबर हों; या (iii)विकर्ण परस्पर समद्विभाजित करते हों; या (iv)सम्मुख भुजाओं का एक युग्म बराबर हो और समान्तर हो।
(5.)आयत के विकर्ण परस्पर समद्विभाजित करते हैं और बराबर होते हैं।इसका विलोम भी सत्य है।
(6.)समचतुर्भुज के विकर्ण परस्पर समकोण पर समद्विभाजित करते हैं।इसका विलोम भी सत्य है।
(7.)वर्ग के विकर्ण परस्पर समकोण पर समद्विभाजित करते हैं।इसका विलोम भी सत्य है।
(8.)किसी त्रिभुज की किन्हीं दो भुजाओं के मध्य-बिन्दुओं को मिलाने वाला रेखाखण्ड तीसरी भुजा के समान्तर होता है और उसका आधा होता है।
(9.)किसी त्रिभुज की एक भुजा के मध्य-बिन्दु से दूसरी भुजा के समान्तर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है।
(10.)किसी चतुर्भुज की भुजाओं के मध्य-बिन्दुओं को एक ही क्रम में मिलाने वाले रेखाखण्डों द्वारा बना चतुर्भुज एक समान्तर चतुर्भुज होता है।
उपर्युक्त प्रश्नों के उत्तर द्वारा मध्य-बिन्दु प्रमेय कक्षा 9 (Mid-Point Theorem Class 9),मध्य-बिन्दु प्रमेय (Mid-Point Theorem) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Mid-Point Theorem Class 9
मध्य-बिन्दु प्रमेय कक्षा 9
(Mid-Point Theorem Class 9)
Mid-Point Theorem Class 9
मध्य-बिन्दु प्रमेय कक्षा 9 (Mid-Point Theorem Class 9) एक त्रिभुज की भुजाओं के मध्य
बिन्दुओं से सम्बन्धित है।इस आर्टिकल में मध्य-बिन्दु प्रमेय और इस पर आधारित उदाहरणों का
अध्ययन करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.