Median and Average in Statistics

Mathematics Satyam December 17, 2023 Statistics No Comments

Contents hide

1 1.सांख्यिकी में मध्यका तथा औसत (Median and Average in Statistics),बहुलक तथा समान्तर माध्य (Mode and Arithmetic Mean):

1.1 2.सांख्यिकी में मध्यका तथा औसत के उदाहरण (Median and Average in Statistics Examples):

1.2 3.सांख्यिकी में मध्यका तथा औसत के सवाल (Median and Average in Statistics Questions):

1.2.1 4.सांख्यिकी में मध्यका तथा औसत (Frequently Asked Questions Related to Median and Average in Statistics),बहुलक तथा समान्तर माध्य (Mode and Arithmetic Mean) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:

1.2.2 प्रश्न:1.मध्यका ज्ञात करने के सूत्र लिखो। (Write the Formulas for Finding Median):

1.2.3 प्रश्न:2.समान्तर माध्य ज्ञात करने के सूत्र लिखो। (Write the Formulas for Finding Arithmetic Mean):

1.2.4 प्रश्न:3.माध्यों की परिसीमाएँ क्या हैं? (What are Limitations of Averages?):

1.2.4.1 Median and Average in Statistics

2 सांख्यिकी में मध्यका तथा औसत (Median and Average in Statistics)

2.1 Median and Average in Statistics

1.सांख्यिकी में मध्यका तथा औसत (Median and Average in Statistics),बहुलक तथा समान्तर माध्य (Mode and Arithmetic Mean):

Median and Average in Statistics

सांख्यिकी में मध्यका तथा औसत (Median and Average in Statistics) के इस आर्टिकल में बहुलक,मध्यका,समान्तर माध्य,चतुर्थकों तथा शतमक पर आधारित सवालों को हल करके समझने का प्रयास करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:- Arithmetic Mean and Mode in Statistics

2.सांख्यिकी में मध्यका तथा औसत के उदाहरण (Median and Average in Statistics Examples):

Example:61.निम्नलिखित सारणी से श्रमिकों की मध्यका आय,मध्य के 80% श्रमिकों की आय का विस्तार तथा बहुलक आय का निर्धारण कीजिए:
(From the following table ascertain Median income,Range of income of middle 80% workers and Modal income of the workers):

$\begin{array}{|cc|} \hline \text { Wages in Rs. } & \text {No. of Workers } \\ \hline \text { Below 10 } & 5 \\ \hline \text { Below 20 } & 8 \\ \hline \text { Below 30 } & 15 \\ \hline 30-40 & 20 \\ \hline 40-50 & 30 \\ \hline 50-60 & 33 \\ \hline 60-70 & 35 \\ \hline \end{array}$
Solution:Calculation Table of Median,Mode and Percentile etc.

$\begin{array}{|ccc|} \hline \text { Wages in Rs. } & \text {No. of Workers } & cf \\ \hline 0-10 & 5 & 5 \\ \hline 10-20 & 3 & 8\\ \hline 20-30 & 7 & 15 \\ \hline 30-40 & 20 & 35 \\ \hline 40-50 & 30 & 65\\ \hline 50-60 & 33 & 98 \\ \hline 60-70 & 35 & 133 \\ \hline Total & 133 & \\ \hline \end{array} \\ m=\frac{N}{2}=\frac{133}{2}=66.5$
It falls in 98cf,whose value is 50-60 group
$l_1=50, i=60-50=10,f=33, c=65$
मध्यका $(M)=l_1+\frac{i}{f}(m-c) \\ =50+\frac{10}{33}(66.5-65) \\ =50+\frac{10}{33} \times 1.5 \\ M=50+0.4545 \approx 50.45 \\ P_{90}=\frac{90 \mathrm{~N}}{100}=\frac{90 \times 133}{100}=119.7$
It falls in 60-70 group
$l_1=60, i=70-60=100, f=35, c=98 \\ P_{90} =l_1+\frac{i}{f}\left(p_{90}-c\right) \\ =60+\frac{10}{35}(119.7-98) \\ =60+\frac{2}{7} \times 21.7 \\ =60+62 \\ \Rightarrow P_{90}=66.20 \\ P_{10}=\frac{10 N}{100}=\frac{10 \times 133}{100}=13.3$
It falls in 20-30 group
$l_1=20, i=30-20=10, f=7, c=8 \\ P_{10} =l_1+\frac{i}{f}\left(p_{10}-c\right) \\ =20+\frac{10}{7}(13.3-8) \\ =20+\frac{10}{7} \times 5.3 \\=20+7.5714 \\ =27.5714 \\ \Rightarrow P_{10}=27.57$
Range of middle 80%=66.20-22.57=38.63
बहुलक (Mode)
निरीक्षण द्वारा बहुलक group 60-70
$l_1=60, i=70-60=10 \\ f_1=35, f_0=33, f_2=0 \\ \Delta_1=f_1-f_0=35-33=2 \\ \Delta_2=f_1-f_2=35-0=35$
बहुलक $(Z)=l_1+\frac{\Delta_1}{\Delta_1+\Delta_2} \times i \\ =60+\frac{2}{2+35} \times 10 \\ =60+\frac{20}{37} \\=60+0.5405 \\ \Rightarrow Z \approx 60.54$
समूहीकरण द्वारा

$\begin{array}{|p{2cm}|p{2cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|} \hline Wages & Frequency (f) & \multicolumn{2}{|c|}{\text{Grouping by two's}} & \multicolumn{3}{|c|}{\text{Grouping by Three's}} & \multicolumn{2}{|c|}{\text{Analysis No. of itmes}} \\ \hline & 1 & 2 & 3 & 4 & 5 & 6 & \multicolumn{2}{|c|} {7} \\ \hline 0-10 & 5 & 8 & & 15 & & & & \\ \cline{1-2} \cline{4-4} \cline{6-9} 10-20 & 3 & & 10 & & 30 & & & \\ \cline{1-3} \cline{7-9} 20-30 & 7 & 27 & & & & 57 & I & 1 \\ \cline{1-2} \cline{4-5} \cline{8-9} 30-40 & 20 & & 50 & 83 & & & II & 2 \\ \cline{1-3} \cline{6-6} \cline{8-9} 40-50 & 30 & 63 & & & 98 & & IIII & 4 \\ \cline{1-2} \cline{4-4} \cline{7-9} 50-60 & 33 & & 68 & & & & IIII & 4 \\ \cline{1-3} \cline{5-5} \cline{8-9} 60-70 & 35 & & & & & & III & 3 \\ \hline \end{array}$
उपर्युक्त विश्लेषण से स्पष्ट है कि बहुलक 40-50 तथा 50-60 दोनों ही वर्गों में आता है क्योंकि दोनों ही वर्ग चार-चार बार आवृत्त होते हैं।इस स्थिति में बहुलक वर्ग का निर्धारण करने में निम्नलिखित विधि अपनाएंगे:
$\begin{array}{|ccc|} \hline \text { वर्ग (class intervals) } & 40-50 & 50-60 \\ \hline \text { वर्ग की आवृत्ति } & 30 & 33 \\ \hline \text { उससे पहले वर्ग की आवृत्ति } & 20 & 30 \\ \hline \text { उसके बाद वाले वर्ग की आवृत्ति } & 33 & 35 \\ \hline \text{ योग } & 83 & 98 \\ \hline \end{array}$
अतः बहुलक वर्ग 50-60 है।
$l_1=50, i=60-50=10 \\ f_1=33, f_0-30, f_2=35 \\ \Delta_1=f_1-f_0 =33-30=3 \\ \Delta_2=f_1-f_2 =33-35=2$
बहुलक $(Z)=l_1+\frac{\Delta_1}{\Delta_1+\Delta_2} \times i \\ =50+\frac{3}{3+2} \times 10 \\ =50+\frac{30}{5} \\ =50+6 \\ \Rightarrow z=56$
Example:62.निम्नलिखित समंकों से समान्तर माध्य तथा मध्यका ज्ञात कीजिए और माध्यों के पारस्परिक सम्बन्ध के आधार पर बहुलक मूल्य का अनुमान लगाइए:
(From the following data calculate Mean and Median and on the basis of empirical relationship between averages,estimate the modal value):

$\begin{array}{|cc|} \hline \text { Marks } & \text {No. of students } \\ \hline \text { Less than 5 } & 7 \\ \hline \text { Less than 10 } & 20 \\ \hline 5-15 & 38 \\ \hline \text{15 and above } & 55 \\ \hline 20-25 & 20 \\ \hline \text{25 and above } & 5 \\ \hline \text{30 and above } & 1 \\ \hline \end{array}$
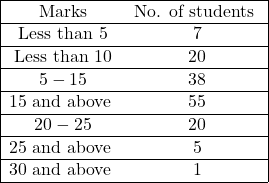
Solution:Calculation Table of Mean and Median

$\begin{array}{|cccccc|} \hline \text { Marks } & \text {No. of students } & \text{M.V.} & dx & fdx & cf \\ & (f) & (x) &A=17.5 & & \\ \hline 0-5 & 7 & 2.5 & -15 & -105 & 7 \\ \hline 5-10 & 13 & 7.5 & -10 & -130 & 20 \\ \hline 10-15 & 25 & 12.5 & -5 & -125 & 45 \\ \hline 15-20 & 30 & 17.5 & 0 & 0 & 75 \\ \hline 20-25 & 20 & 22.5 & 5 & 100 & 95 \\ \hline 25-30 & 4 & 27.5 & 10 & 40 & 99 \\ \hline 30-35 & 1 & 37.5 & 15 & 15 & 100 \\ \hline \text{Total} & 100 & & & -205 & \\ \hline \end{array}$
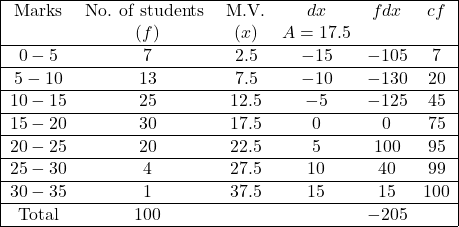
समान्तर माध्य $(\overline{X})=A+\frac{\Sigma f d x}{N} \\ =17.5+\frac{(-205)}{100} \\ =17.5-2.05 \\ \overline{X}=15.45 \\ m=\frac{N}{2}=\frac{100}{2}=50$
It falls in 75cf,whose value is 15-20 group
$l_1=15, i =20-15=5, f=30, c=45$
मध्यका $(M)=l_1+\frac{i}{f}(m-c) \\ =15+\frac{5}{30}(50-45) \\ =15+\frac{1}{6} \times 5 \\ =15+0.833 \\ \Rightarrow M \approx 15.83$
बहुलक का अनुमानित मान $Z=3 M-2 \overline{X} \\ =3 \times 15.83-2 \times 15.45 \\ =47.49-30.90 \\ \Rightarrow Z=16.59$
निरीक्षण द्वारा बहुलक
बहुलक समूह 15-20
$l_1=15, i=20-15=5 \\ f_0=25, f_1=30, f_2=20 \\ \Delta_1=f_1-f_0=30-25=5 \\ \Delta_2=f_1-f_2=30-20=10$
बहुलक $(Z)=l_1+\frac{\Delta_1}{\Delta_1+\Delta_2} \times i \\ =15+\frac{5}{5+10} \times 5 \\ =15+\frac{25}{15} \\ =15+1.666 \\ \Rightarrow Z \approx 16.67$
Example:63.निम्नलिखित समंकों के समान्तर माध्य,मध्यका तथा बहुलक ज्ञात कीजिए:
(Calculate Arithmetic Mean,Median and Mode of the following data):

$\begin{array}{|cc|} \hline \text { Class } & \text { Frequency } \\ \hline 75-80 & 5 \\ 70-75 & 7 \\ 60-70 & 15 \\ 53-60 & 18 \\ 50-53 & 7 \\ 46-50 & 12 \\ 40-46 & 18 \\ 37-40 & 5 \\ 34-37 & 7 \\ 30-34 & 7 \\ 25-30 & 8 \\ 20-25 & 4 \\ \hline \end{array}$
Solution:Calculation Table of Mean,Median and Mode

$\begin{array}{|cccccc|} \hline \text { Class } & \text { Frequency } & \text{M.V.} & dx & fdx & cf \\ & (f) & (x) & A=55 & & \\ \hline 20-30 & 12 & 25 & -30 & -360 & 12 \\ 30-40 & 19 & 35 & -20 & -380 & 31 \\ 40-50 & 30 & 45 & -10 & -300 & 61 \\ 50-60 & 25 & 55 & 0 & 0 & 86 \\ 60-70 & 15 & 65 & 10 & 150 & 101 \\ 70-80 & 12 & 75 & 20 & 240 & 113 \\ \hline \text{Total} & 113 & & & -650 & \\ \hline \end{array}$
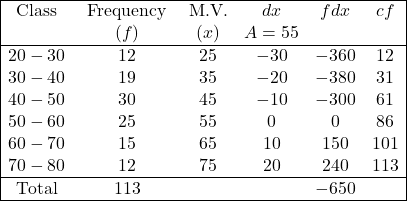
समान्तर माध्य

$(\overline{X})=A+\frac{\Sigma f d x}{N} \\ =55+\frac{(-650)}{113} \\ =55-5.752 \\ =49.248 \\ \Rightarrow \overline{X} =49.25 \\ m=\frac{N}{2}=\frac{113}{2}=56.5$
It falls in 62cf,whose value is 40-50 group
l_1=40, i=50-40=10, f=30, c=31
मध्यका $(M)=l_1+\frac{i}{f}(m-c) \\ =40+\frac{10}{30}(56.5-31) \\ =40+\frac{1}{3}(25.5) \\ =40+8.5 \\ \Rightarrow M=48.5$
बहुलक निरीक्षण द्वारा
बहुलक समूह 40-50 है
$l_1=40, i=50-40=10 \\ f_0=19, f_1=30, f_2=25 \\ \Delta_1=f_1-f_0=30-19=11 \\ \Delta_2=f_1-f_2=30-25=5$
बहुलक $(Z)=l_1+\frac{\Delta_1}{\Delta_1+\Delta_2} \times i \\ =40+\frac{11}{11+5} \times 10 \\ =40+\frac{110}{16} \\ =40+6.875 \\ \Rightarrow Z \approx 46.88$
समूहीकरण द्वारा

$\begin{array}{|p{2cm}|p{2cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|} \hline Class & Frequency (f) & \multicolumn{2}{|c|}{\text{Grouping by two's}} & \multicolumn{3}{|c|}{\text{Grouping by Three's}} & \multicolumn{2}{|c|}{\text{Analysis No. of itmes}} \\ \hline & 1 & 2 & 3 & 4 & 5 & 6 & \multicolumn{2}{|c|} {7} \\ \hline 20-30 & 12 & 31 & & 61 & & & I & 1 \\ \cline{1-2} \cline{4-4} \cline{6-9} 30-40 & 19 & & 49 & & 74 & & III & 3 \\ \cline{1-3} \cline{7-9} 40-50 & 30 & 55 & & & & 70 & IIIII & 6 \\ \cline{1-2} \cline{4-5} \cline{8-9} 50-60 & 25 & & 40 & 52 & & & III & 3 \\ \cline{1-3} \cline{6-6} \cline{8-9} 60-70 & 15 & 27 & & & & & I & 1 \\ \cline{1-2} \cline{4-4} \cline{7-9} 70-80 & 12 & & & & & & & \\ \hline \end{array}$
उपर्युक्त विश्लेषण से स्पष्ट है कि 40-50 वर्ग 6 बार (सबसे अधिक बार) आवृत्त हुआ है जो बहुलक वर्ग है।अतः निरीक्षण और समूहीकरण दोनों से बहुलक समान है।

z \approx 46.88

Median and Average in Statistics

Example:64.निम्न समंकों से मध्यका,चतुर्थक तथा बहुलक मूल्य का निर्धारण कीजिए:
(Determine the values of Median,Quartiles and the Mode from the following data):

$\begin{array}{|cc|} \hline \text { Central Value } & \text { Frequency } \\ \hline 5 & 15 \\ \hline 15 & 20 \\ \hline 25 & 25 \\ \hline 35 & 24 \\ \hline 45 & 12 \\ \hline 55 & 31 \\ \hline 65 & 71 \\ \hline 75 & 62 \\ \hline \end{array}$
Solution:Calculation Table of Median,Mode and Quartiles etc.

$\begin{array}{|ccc|} \hline \text { Class } & \text { Frequency } & cf \\ \hline 0-10 & 15 & 15 \\ \hline 10-20 & 20 & 35 \\ \hline 20-30 & 25 & 60 \\ \hline 30-40 & 24 & 84 \\ \hline 40-50 & 12 & 96 \\ \hline 50-60 & 31 & 127 \\ \hline 60-70 & 71 & 198 \\ \hline 70-80 & 52 & 250 \\ \hline \text{Total} & 250 & \\ \hline \end{array}$

$m=\frac{N}{2}=\frac{250}{2}=125$
It falls in 127cf,whose value is 50-60 group
l_1=50, i=60-50=10 , f=31, c=96

मध्यका $(M)=l_{1}+\frac{i}{f}(\mathrm{~m}-c) \\ =50+\frac{10}{31}(125-96) \\ =50+\frac{10 \times 29}{31} \\ =50+9.354 \\ M \approx 59.35$
Quartile 1st $(Q_1) \\ q_1=\frac{N}{4}=\frac{250}{4}=62.5$
It lies in 84cf whose size is 30-40
$l_1=30, i =40-30=10, f=24, c=60 \\ Q_1=l_1+\frac{i}{f}\left(q_1-c\right) \\ =30+\frac{10}{24}(62.5-60) \\ =30+\frac{5}{12} \times 2.5 \\ =30+1.0416 \\ =31.0416 \\ \Rightarrow Q_1 \approx 31.04$

Quartile 3rd $(Q_3) \\ q_3=\frac{3 N}{4}=\frac{3 \times 250}{4}=187.5$
It lies in 198cf whose size is 60-70
$l_1=66, i=70-60=10, f=71, c=127 \\ Q_3=l_1+\frac{i}{f}\left(q_3-c\right) \\ =60+\frac{10}{71}(187.5-127) \\ =60+\frac{10}{71} \times 60.5 \\ =60+8.521 \\ \Rightarrow Q_3 \approx 68.52$
बहुलक निरीक्षण द्वारा
बहुलक वर्ग 60-70 है क्योंकि इसी वर्ग की बारम्बारता सबसे अधिक है।
$l_1=60, i=70-60=10 \\ f_0=31, f_1=71, f_2=52 \\ \Delta_1=f_1-f_0=71-31=40 \\ \Delta_2=f_1-f_2=71-52=19$
बहुलक $(Z)=l_1+\frac{\Delta_1}{\Delta_1+\Delta_2} \times i \\ =60+\frac{40}{40+15} \times 10 \\ =60+\frac{400}{59} \\ =60+6.779 \\ =66.779 \\ \Rightarrow Z \approx 66.78$
समूहीकरण द्वारा

$\begin{array}{|p{2cm}|p{2cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|} \hline Wages & Frequency (f) & \multicolumn{2}{|c|}{\text{Grouping by two's}} & \multicolumn{3}{|c|}{\text{Grouping by Three's}} & \multicolumn{2}{|c|}{\text{Analysis No. of itmes}} \\ \hline & 1 & 2 & 3 & 4 & 5 & 6 & \multicolumn{2}{|c|} {7} \\ \hline 0-10 & 15 & 35 & & 60 & & & & \\ \cline{1-2} \cline{4-4} \cline{6-9} 10-20 & 20 & & 45 & & 69 & & & \\ \cline{1-3} \cline{7-9} 20-30 & 25 & 49 & & & & 61 & & \\ \cline{1-2} \cline{4-5} \cline{8-9} 30-40 & 24 & & 36 & 67 & & & I & 1 \\ \cline{1-3} \cline{6-6} \cline{8-9} 40-50 & 12 & 43 & & & 114 & & II & 2 \\ \cline{1-2} \cline{4-4} \cline{7-9} 50-60 & 31 & & 102 & & & 154 & IIII & 4 \\ \cline{1-3} \cline{5-5} \cline{8-9} 60-70 & 71 & 123 & & & & & IIIII & 5 \\ \cline{1-2} \cline{4-4} \cline{6-6} \cline{8-9} 70-80 & 52 & & & & & & II & 2 \\ \hline \end{array}$
उपर्युक्त विश्लेषण से स्पष्ट है कि 60-70 वर्ग 5 बार (सबसे अधिक बार) आवृत्त हुआ है जो बहुलक वर्ग है।अतः निरीक्षण और समूहीकरण दोनों से बहुलक समान है। $Z \approx 66.78$
Example:65.निम्न समंकों से माध्य,बहुलक तथा मध्यका परिकलित कीजिए-(i)बिना समान वर्ग-अन्तराल बनाये और (ii)समान वर्ग अन्तराल बनाने के पश्चात।
(Calculate mean,mode and median from the following data:(i)without making equal class-intervals and (ii)making equal class-intervals.)
$\begin{array}{|cc|} \hline \text { Class } & \text { Frequency } \\ \hline 2 & 1 \\ 3 & 2 \\ 4 & 2 \\ 5-7 & 3 \\ 7-10 & 5 \\ 10-15 & 10 \\ 15-20 & 8 \\ 20-25 & 4 \\ \hline \end{array}$
Solution:(i)Calculation Table of Mean,Median

$\begin{array}{|ccccc|} \hline \text { Class } & \text { Frequency } & M.V. & fx & cf \\ & (f) & (x) & & \\ \hline 2 & 1 & 2 & 2 & 1\\ 3 & 2 & 3 & 6 & 3 \\ 4 & 2 & 4 & 8 & 5 \\ 5-7 & 3 & 6 & 18 & 8 \\ 7-10 & 5 & 8.5 & 42.5 & 13 \\ 10-15 & 10 & 12.5 & 125 & 23 \\ 15-20 & 8 & 17.5 & 140 & 31 \\ 20-25 & 4 & 22.5 & 90 & 35 \\ \hline \text{Total} & 35 & & 431.5 & \\ \hline \end{array}$
समान्तर माध्य

$(\overline{X})=\frac{\Sigma f x}{N} \\ =\frac{431.5}{35} \\ =12.328 \\ \overline{X}=12.33 \\ m=\frac{N}{2}=\frac{35}{2}=17.5$
It falls in 23cf,whose value is 10-15 group
l_1=10, i=15-10=5 , f=10, c=13
मध्यका $(M)=l_1+\frac{i}{f}(m-c) \\ =10+\frac{5}{10}(17.5-13) \\ =10+\frac{1}{2} \times 4.5 \\ =10+2.25 \\ M \approx 12.25$
बहुलक $(Z)=3 M-2 \overline{X} \\ =3 \times 12.25-2 \times 12.33 \\ =36.75-24.66 \\ \Rightarrow Z =12.09$
(ii)Calculation Table of Mean,Median and Mode

$\begin{array}{|cccccc|} \hline \text { Class } & \text { Frequency } & M.V. & dx & fdx & cf \\ & (f) & (x) & A=12.5 & \\ \hline 0-5 & 5 & 2.5 & -10 & -50 & 5 \\ 5-10 & 8 & 7.5 & -5 & -40 & 13 \\ 10-15 & 10 & 12.5 & 0 & 0 & 23 \\ 15-20 & 8 & 17.5 & 5 & 40 & 31 \\ 20-25 & 4 & 22.5 & 10 & 40 & 35 \\ \hline \text{Total} & 35 & & & -10 & \\ \hline \end{array}$
समान्तर माध्य $(\overline{X})=A+\frac{\Sigma f d x}{N} \\ =12.5-\frac{10}{35} \\ =12.5-\frac{2}{7} \\ =12.5-0.285 \\ =12.215 \\ \overline{X} \approx 12.22 \\ m=\frac{N}{2}=\frac{35}{2}=17.5$
It falls in 23cf,whose value is 10-15 group
$l_1=10, i=15-10=5, f=10, c=13$
मध्यका $(M)=l_1+\frac{i}{f}(M-c) \\ =10+\frac{5}{10}(12 \cdot 5-13) \\ =10+\frac{1}{2} \times 4.5 \\ =10+2.25 \\ \Rightarrow M \approx 12.25$
बहुलक निरीक्षण द्वारा
बहुलक वर्ग 10-15 है क्योंकि इसी वर्ग की बारम्बारता सबसे अधिक है।
$l_1=10,i=15-10=5 \\ f_0 =8, f_1=10, f_2=8 \\ \Delta_1 =f_1-f_0=10-8=2 \\ \Delta_2=f_1-f_2 =10-8=2$
बहुलक $(Z)=l_1+\frac{\Delta_1}{\Delta_1+\Delta_2} \times i \\ =10+\frac{2}{2+2} \times 5 \\ =10+\frac{2}{4} \times 5 \\ =10+\frac{10}{4} \\ =10+2.5 \\ \Rightarrow Z=12.5$
समूहीकरण द्वारा

$\begin{array}{|p{2cm}|p{2cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|p{1cm}|} \hline Class & Frequency (f) & \multicolumn{2}{|c|}{\text{Grouping by two's}} & \multicolumn{3}{|c|}{\text{Grouping by Three's}} & \multicolumn{2}{|c|}{\text{Analysis No. of itmes}} \\ \hline & 1 & 2 & 3 & 4 & 5 & 6 & \multicolumn{2}{|c|} {7} \\ \hline 0-5 & 5 & 13 & & 23 & & & I & 1 \\ \cline{1-2} \cline{4-4} \cline{6-9} 5-10 & 8 & & 18 & & 26 & & III & 3 \\ \cline{1-3} \cline{7-9} 10-15 & 10 & 18 & & & & 22 & IIIII & 6 \\ \cline{1-2} \cline{4-5} \cline{8-9} 15-20 & 8 & & 12 & & & & III & 3 \\ \cline{1-3} \cline{6-6} \cline{8-9} 20-25 & 4 & & & & & & I & 1 \\ \hline \end{array}$
उपर्युक्त विश्लेषण से स्पष्ट है कि 10-15 वर्ग 6 बार (सबसे अधिक बार) आवृत्त हुआ है जो बहुलक वर्ग है।अतः निरीक्षण तथा समूहीकरण दोनों से बहुलक समान है।
उपर्युक्त उदाहरणों के द्वारा सांख्यिकी में मध्यका तथा औसत (Median and Average in Statistics),बहुलक तथा समान्तर माध्य (Mode and Arithmetic Mean) को समझ सकते हैं।

3.सांख्यिकी में मध्यका तथा औसत के सवाल (Median and Average in Statistics Questions):

Median and Average in Statistics

(1.)बच्चों के एक क्लब के सदस्यों का आयु-बंटन निम्न प्रकार है:
(The age-distribution of the members of a certain children’s club is as follows):

$\begin{array}{|cc|} \hline \text { Age last birthday } & \text { Frequency }\\ \text{(years)} & \\ \hline 4 & 5 \\ \hline 5 & 9 \\ \hline 6 & 18 \\ \hline 7 & 35 \\ \hline 8 & 42 \\ \hline 9 & 32 \\ \hline 10 & 15 \\ \hline 11 & 7 \\ \hline 12 & 3 \\ \hline \end{array}$
क्लब में एक सदस्य A ऐसा है कि उससे जितने सदस्य आयु में छोटे हैं उसके दो गुने सदस्य उससे आयु में बड़े हैं।A की आयु को दशमलव अंकों तक (वर्षों में) ज्ञात कीजिए।
(There is a member A such that there are twice as many members older than A as there are members younger than A.Estimate his age in years upto two decimal places.)
(2.)बनारस के साड़ी बुनकरों के एक निश्चित वर्ग के लिए मध्यका और चतुर्थक आय क्रमशः 44.3 रु.,43 रु. और 45.9 रु. प्रति सप्ताह है।मजदूरी का वर्ग विस्तार 40 और 50 रु. के बीच है।वर्ग के 10% बुनकर 42 रु. से कम कमाते हैं,13% 47रु. और उससे अधिक और 6% 48रु. और अधिक कमाते हैं।इन तथ्यों को एक आवृत्ति बंटन के रूप में प्रस्तुत कीजिए और माध्य मजदूरी ज्ञात कीजिए।
(For a certain group of ‘saree’ weavers of Banaras,the median and quartile earnings per week are Rs.44.3,Rs.43.0 and Rs.45.9 respectively.The earnings for the group range between Rs.40 and 50.Ten percent of the group earn under Rs.42 per week,13 percent Rs.47 and over and 6 percent Rs.48 and over.Put this data into the form of a frequency distribution and obtain estimate of the mean wage.)
उत्तर (Answers):(1.)आयु 7.69 वर्ष

(2.) $\begin{array}{|cc|} \hline \text { Wages(Rs.) } & \text { Frequency } \\ \hline 40-42 & 10 \\ \hline 42-43 & 15 \\ \hline 43-44.3 & 25 \\ \hline 44.3-45.9 & 25 \\ \hline 45.9-47 & 12 \\ \hline 47-48 & 7 \\ \hline 48-50 & 6 \\ \hline \end{array}$

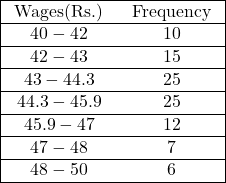
$\overline{X}=44.5$ Rs.
उपर्युक्त सवालों को हल करने पर सांख्यिकी में मध्यका तथा औसत (Median and Average in Statistics),बहुलक तथा समान्तर माध्य (Mode and Arithmetic Mean) को ठीक से समझ सकते हैं।

Also Read This Article:- Mode and Arithmetic Mean in Statistics

4.सांख्यिकी में मध्यका तथा औसत (Frequently Asked Questions Related to Median and Average in Statistics),बहुलक तथा समान्तर माध्य (Mode and Arithmetic Mean) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:

प्रश्न:1.मध्यका ज्ञात करने के सूत्र लिखो। (Write the Formulas for Finding Median):

उत्तर:(1.)व्यक्तिगत श्रेणी (Individual Observations)
M=size of $\left(\frac{N+1}{2}\right)$ item
(2.)खण्डित श्रेणी (Discrete Series)
M=size of $\left(\frac{N+1}{2}\right)$ item
(3.)सतत श्रेणी (Continuous Series)
M=size of $\left(\frac{N}{2}\right)$ item
मध्यका वर्ग में $M=l_1+\frac{i}{f}(m-c)$

प्रश्न:2.समान्तर माध्य ज्ञात करने के सूत्र लिखो। (Write the Formulas for Finding Arithmetic Mean):

उत्तर:(1.)व्यक्तिगत श्रेणी (Individual Observations)
प्रत्यक्ष रीति (Direct Method) $\overline{X}=\frac{ \Sigma X}{N}$
लघुरीति (Short-cut Method) $\overline{X}=A+\frac{ \Sigma d x}{N}$
(2.)खण्डित श्रेणी (Discrete Series)
प्रत्यक्ष रीति (Direct Method) $\overline{X}=\frac{ \Sigma fx}{N}$
लघुरीति (Short-cut Method) $\overline{X}=A+\frac{ \Sigma f dx}{N}$
(3.)सतत श्रेणी (Continuous Series)
प्रत्यक्ष रीति (Direct Method) $\overline{X}=\frac{ \Sigma fx}{N}$
लघुरीति (Short-cut Method) $\overline{X}=A+\frac{ \Sigma f dx}{N}$
पद-विचलन रीति (समान वर्गान्तर) (Step Deviation Method)
$\overline{X}=A+\frac{ \Sigma f dx'}{N} \times i$

प्रश्न:3.माध्यों की परिसीमाएँ क्या हैं? (What are Limitations of Averages?):

उत्तर:माध्य श्रेणी का मात्र एक अकेला समंक है जो श्रेणी के गुणों का प्रतिनिधित्व करता है,परंतु सभी मूल्यों के गुणों का वर्णन नहीं करता है।अतः यह आवश्यक है कि माध्य का निर्वचन उचित सावधानी के साथ किया जाए।अन्य शब्दों में माध्य की यह सीमा है कि वह श्रेणी की बनावट,व्यक्तिगत मूल्य का माध्यों से अंतर तथा उसकी विषमता के संबंध में पूरी जानकारी नहीं देता।अनेक बार माध्य मूल्य ऐसा मूल्य होता है जो श्रेणी में किसी भी मद का मूल्य नहीं होता है।कभी-कभी दो या अधिक फर्मों के लाभों का माध्य समान हो सकता है,किंतु उनकी उपार्जन शक्ति की स्थिति भिन्न हो सकती है।संभव है एक के लाभ निरंतर गिर रहे हों,एक के स्थिर हों और एक में लगातार वृद्धि हो रही हो जबकि तीनों का माध्य एकसमान है।श्रेणी की बनावट के बारे में ज्ञान प्राप्त करने के लिए ही अपकिरण का अध्ययन किया जाता है।
उपर्युक्त प्रश्नों के उत्तर द्वारा सांख्यिकी में मध्यका तथा औसत (Median and Average in Statistics),बहुलक तथा समान्तर माध्य (Mode and Arithmetic Mean) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Instagram	click here
4.	Linkedin	click here
5.	Facebook Page	click here
6.	Twitter	click here

Median and Average in Statistics

सांख्यिकी में मध्यका तथा औसत
(Median and Average in Statistics)

Median and Average in Statistics

About Author

Satyam

About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.