Mean in Statistics

Mathematics Satyam August 11, 2023 Statistics No Comments

Contents hide

1 1.सांख्यिकी में माध्य (Mean in Statistics),सांख्यिकीय माध्य (Statistical Mean):

1.1 2.सांख्यिकी में माध्य के उदाहरण (Mean in Statistics Examples):

1.2 3.सांख्यिकी में माध्य के सवाल (Mean in Statistics Questions):

1.2.1 4.सांख्यिकी में माध्य (Frequently Asked Questions Related to Mean in Statistics),सांख्यिकीय माध्य (Statistical Mean) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:

1.2.2 प्रश्न:1.केन्द्रीय प्रवृत्ति के माप से क्या आशय है? (What Do You Mean by Measures of Central Tendency?):

1.2.3 प्रश्न:2.समान्तर माध्य की परिभाषा दीजिए। (Define Arithmetic Mean):

1.2.4 प्रश्न:3.सांख्यिकी माध्य के दो उद्देश्य बताइए। (State Two Objects of Statistical Averages):

1.2.4.1 Mean in Statistics

2 सांख्यिकी में माध्य (Mean in Statistics)

2.1 Mean in Statistics

1.सांख्यिकी में माध्य (Mean in Statistics),सांख्यिकीय माध्य (Statistical Mean):

Mean in Statistics

सांख्यिकी में माध्य (Mean in Statistics) केन्द्रीय प्रवृत्ति का माप है।सांख्यिकीय विश्लेषण का मुख्य उद्देश्य विशाल समंकों को संक्षिप्त तथा उपयोगी एवं तुलनीय बनाना है और इस कार्य के लिए समंकमाला में निहित केन्द्रीय प्रवृत्ति का अध्ययन महत्त्वपूर्ण है।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:-Regression Equations in Statistics

2.सांख्यिकी में माध्य के उदाहरण (Mean in Statistics Examples):

Example:1.निम्नलिखित स्थितियों में समान्तर माध्य का निर्धारण कीजिए:
(Determine arithmetic mean in the following cases):
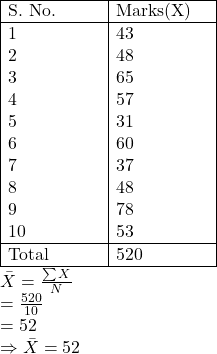
Example:1(i).दस विद्यार्थियों द्वारा एक परीक्षा में प्राप्त अंक:
43,48,65,57,31,60,37,48,78,53
Solution:Calculation of Arithmetic Mean by Direct Method

$\begin{array}{ |p{2cm}|p{2cm}|} \hline S. No. & \text{Marks(X)} \\ \hline 1 & 43 \\ 2 & 48 \\ 3 & 65 \\ 4 & 57 \\ 5 & 31\\ 6 & 60\\ 7 & 37\\ 8 & 48 \\ 9 & 78 \\ 10 & 53 \\ \hline \text{Total} & 520 \\ \hline \end{array} \\ \bar{X}=\frac{\sum X}{N} \\ =\frac{520}{10} \\ =52 \\ \Rightarrow \bar{X} =52$
Example:1(ii).एक वैज्ञानिक द्वारा एक सिलिण्डर (cylinder) के व्यास (diameter) के माप का आलेखन:
38.8,40.9,39.2,39.7,40.2,39.5,40.3,39.2,39.8,40.6 मिलीमीटर
Solution:Calculation of Arithmetic Mean by Direct Method

$\begin{array}{ |p{2cm}|p{2cm}|} \hline S. No. & \text{Diameter} \\ \hline 1 & 38.8 \\ 2 & 40.9 \\ 3 & 39.2 \\ 4 & 39.7 \\ 5 & 40.2 \\ 6 & 39.5 \\ 7 & 40.3 \\ 8 & 39.2 \\ 9 & 39.8 \\ 10 & 40.6 \\ \hline \text{Total} & 398.2 \\ \hline \end{array} \\ \bar{X} =\frac{\Sigma X}{N} \\ =\frac{398.2}{10} \\ =39.82 \\ \Rightarrow \overline{X} =39.82 \mathrm{~mm}$
Example:1(iii).एक फर्म में कार्य कर रहे 14 कर्मचारियों का वार्षिक वेतन:
5000,6000,6500,8300,30000,13000,10000,22500,17500,5200,8800,16000,20000,4800
Solution:Calculation of Arithmetic Mean by Direct Method

$\begin{array}{ |p{2cm}|p{2cm}|} \hline S. No. & \text{Marks(X)} \\ \hline 1 & 5000 \\ 2 & 6000 \\ 3 & 6500 \\ 4 & 8300 \\ 5 & 30000 \\ 6 & 13000 \\ 7 & 10000 \\ 8 & 22500 \\ 9 & 17500 \\ 10 & 5200 \\ 11 & 8800 \\ 12 & 16000 \\ 13 & 20000 \\ 14 & 4800 \\ \hline \text{Total} & 173600 \\ \hline \end{array} \\ \bar{X} =\frac{\sum X}{N} \\ =\frac{173600}{14} \\ =\text{Rs.} 12,400 \\ \Rightarrow \overline{X}=\text{Rs.} 12,400$
Example:2(a).एक सौ संख्याओं में 4 बीस बार,5 चालीस बार,6 तीस बार तथा शेष 7 हैं।इन संख्याओं का समान्तर माध्य ज्ञात कीजिए।
(Out of 100 numbers,20 were 4’s,40 were 5’s,30 were 6’s, and the remainder were 7’s.Find arithmetic mean of the numbers)
Solution: $\bar{X}=\frac{\Sigma X}{N} \\ \bar{X}= \frac{4 \times 20+5 \times 40+6 \times 30+7 \times 10}{100} \\ =\frac{80+200+180+70}{100} \\ \Rightarrow \bar{X} =5.3 \text { Numbers}$
Example:2(b).निम्न सारणियों में प्रस्तुत समंकों का समान्तर माध्य ज्ञात कीजिए:
Example:2(b)(i). $\begin{array}{ |p{3cm}|p{3cm}|} \hline Time(Seconds) & \text{No. of persons} \\ \hline 58 & 8 \\ 61 & 5 \\ 65 & 12 \\ 67 & 5\\ 68 & 4 \\ 70 & 3 \\ 72 & 3 \\ \hline \end{array}$
Solution:Calculation of Arithmetic Mean by Direct Method

$\begin{array}{ |p{3cm}|p{3cm}|p{3cm}|} \hline Time(Seconds) & \text{No. of persons} & fx \\ \hline 58 & 8 & 464 \\ 61 & 5 & 305\\ 65 & 12 & 780 \\ 67 & 5 & 335\\ 68 & 4 & 272 \\ 70 & 3 & 210\\ 72 & 3 & 216\\ \hline Total & 40 & 2582\\ \hline \end{array} \\ \overline{X} =\frac{\Sigma f x}{\Sigma f} \\ =\frac{2582}{40} \\ =64.55 \\ \Rightarrow \overline{X} =64.55 \text { seonds }$
Example:2(b)(ii). $\begin{array}{ |p{2cm}|p{2cm}|} \hline \text{length} & \text{Number} \\ \hline 5 & 10 \\ 5.5 & 33 \\ 6 & 70\\ 6.5 & 110\\ 7 & 176\\ 7.5 & 172\\ 8 & 124 \\ 8.5 & 61 \\ 9 & 32 \\ 9.5 & 12\\ \hline \end{array}$
Solution:Calculation of Arithmetic Mean by Direct Method

$\begin{array}{ |p{2cm}|p{2cm}|p{2cm}|} \hline \text{length} & \text{Number} \\ \hline 5 & 10 & 50 \\ 5.5 & 33 & 181.5 \\ 6 & 70 & 420 \\ 6.5 & 110 & 715 \\ 7 & 176 & 1232 \\ 7.5 & 172 & 1290 \\ 8 & 124 & 992 \\ 8.5 & 61 &518.2 \\ 9 & 32 & 288 \\ 9.5 & 12 & 114\\ \hline total & 800 & 5801 \\ \hline \end{array} \\ \overline{X}=\frac{\Sigma f x}{\Sigma f} \\ =\frac{5801}{800} \\ =7.25125 \\ \Rightarrow \overline{X} \approx 7.25 \text { (Appox.) }$
Example:3.विद्यालय के 100 विद्यार्थियों ने एक समारोह में निम्नलिखित चन्दा दिया
(100 students of Vidya Ashram school gave donations)
10 students donate (चन्दा देते हैं) Rs.5 each
10 students donate (चन्दा देते हैं) Rs.4 each
24 students donate (चन्दा देते हैं) Rs.3 each
30 students donate (चन्दा देते हैं) Rs.2 each
21 students donate (चन्दा देते हैं) Rs.1 each
चन्दे के समान्तर माध्य की गणना कीजिए:
(calculate arithmetic mean of donations)
Solution:Calculation of Arithmetic Mean by Direct Method

$\begin{array}{ |p{2cm}|p{2cm}|p{2cm}|} \hline Donations (X) & No of students (f) & fx \\ \hline 5 & 10 & 50 \\ 4 & 15 & 60 \\ 3 & 24 & 72 \\ 2 & 30 & 60 \\ 1 & 21 & 21 \\ \hline Total & 100 & 263 \\ \hline \end{array} \\ \overline{X}=\frac{\Sigma f x}{\Sigma f} \\ =\frac{263}{100} \\ =\text{Rs.} 2.63 \\ \Rightarrow \overline{X} =\text{Rs.} 2.63$
Example:4.एक क्लब ने एक समूह के समय में 50 मैच खेले और निम्नलिखित गोल किए:
(i)गोल करने का औसत (ii)एक दिन में खेले गए औसत मैचों की संख्या ज्ञात कीजिए।
(A club played 50 matches during a week’s time and scored the following number of goals.Calculate:
(i)The average goals scored,and
(ii)the average matches played per day

$\begin{array}{ |p{2cm}|p{3cm}|p{3cm}|} \hline Days & No of matches played & Total No. of goals scored \\ \hline Sunday & 10 & 20 \\ Monday & 15 & 45 \\ Tuesday & 10 & 25 \\ Wednesday & 8 & 10 \\ Thrusday & 4 & 0 \\ Friday & 0 & 0 \\ Saturday & 3 & 10 \\ \hline \end{array}$
Solution:Calculation of Arithmetic Mean by Direct Method

$\begin{array}{ |p{2cm}|p{3cm}|p{3cm}|} \hline Days & No of matches played(X) & Total No. of goals scored(Y) \\ \hline Sunday & 10 & 20 \\ Monday & 15 & 45 \\ Tuesday & 10 & 25 \\ Wednesday & 8 & 10 \\ Thrusday & 4 & 0 \\ Friday & 0 & 0 \\ Saturday & 3 & 10 \\ \hline Total & 50 & 110 \\ \hline \end{array}$

(i) $\overline{X}=\frac{\Sigma X}{N}=\frac{110}{50}=2.2 \text{ goals}$
(ii) $\overline{X}=\frac{\Sigma x}{N}=\frac{50}{7}=7.1428 \\ \overline{X} \approx 7.14 \text{ matches}$
Example:5.निम्नलिखित समंकों से समान्तर माध्य का मूल्य ज्ञात कीजिए:
(From the following data find out the value of mean):

$\begin{array}{ |p{2cm}|p{2cm}|} \hline Age in Years & No. of persons \\ \hline 10-20 & 2 \\ 20-30 & 4 \\ 30-40 & 4 \\ 40-50 & 8 \\ 50-60 & 6\\ 60-70 & 3\\ 70-80 & 2 \\ \hline \end{array}$
Solution:Calculation of Arithmetic Mean by Direct Method

$\begin{array}{ |p{2cm}|p{2cm}|p{2cm}|p{2cm}|} \hline Age in Years & No. of persons & Mid values & fx \\ \hline 10-20 & 2 & 15 & 30\\ 20-30 & 4 & 25 & 100\\ 30-40 & 4 & 35 & 140 \\ 40-50 & 8 & 45 & 360\\ 50-60 & 6 & 55 & 330 \\ 60-70 & 3& 65 & 195\\ 70-80 & 2 & 75 & 150\\ \hline total & 29 & & 1305 \\ \hline \end{array} \\ \overline{X}=\frac{\Sigma f x}{\Sigma f} \\ =\frac{1305}{29} \\ =45 \\ \Rightarrow \overline{X}=45$

Mean in Statistics

Example:6.एक कम्पनी अपने स्टाफ के सदस्यों को बोनस देना चाहती है।बोनस निम्नवत दिया जाता है:
(A company wants to pay bonus to the members of the staff.The bonus is to be paid as under):

$\begin{array}{ |p{7cm}|p{2cm}|} \hline Monthly Salary & Bonus(Rs.) \\ \hline Rs. 100 and not exceeding Rs. 120 & 50 \\ Rs. 120 and not exceeding Rs. 140 & 60 \\ Rs. 140 and not exceeding Rs. 160 & 70 \\ Rs. 160 and not exceeding Rs. 180 & 80 \\ Rs. 180 and not exceeding Rs. 200 & 90 \\ Rs. 200 and not exceeding Rs. 220 & 100 \\ Rs. 220 and over & 110 \\ \hline \end{array}$
Actual salary was (वास्तविक वेतन इस प्रकार था):
Rs.200,180,195,218,187,160,250,198,190,168,170,178,175,140,120,148,165,155,145,125,110,162,130,150,185
कुल बोनस क्या है? कर्मचारियों को दिया गया बोनस क्या है?
(What is the total bonus paid? What is the average bonus paid per employee?)
Solution:Calculation of Arithmetic Mean by Direct Method

$\begin{array}{ |p{3cm}|p{3cm}|p{3cm}|} \hline Salary & \text{No. of Employee} & Bonus(X) \\ \hline 110 & 1 & 50 \\ 120 & 1 & 60 \\ 125 & 1 & 60 \\ 130 & 1 & 60 \\ 140 & 1 & 70 \\ 145 & 1 & 70 \\ 148 & 1 &70 \\ 150 & 1 & 70 \\ 155 & 1 & 70 \\ 160 & 1 & 80\\ 162 & 1 & 80 \\ 165 & 1 & 80 \\ 168 & 1 & 80 \\ 170 & 1 & 80\\ 175 & 1 & 80 \\ 178 & 1 & 80 \\ 180 & 1 & 90 \\ 185 & 1 & 90 \\ 187 & 1 & 90 \\ 190 & 1 & 90 \\ 195 & 1 & 90 \\ 198& 1 & 90 \\ 200 & 1 & 100\\ 218 & 1 & 100 \\ 250 & 1 & 110 \\ \hline Total & 25 & 1990 \\ \hline \end{array}$

Total Bonus =1990 Rs.
$\overline{X} =\frac{\Sigma x}{10}=\frac{1990}{25} \\ \Rightarrow \overline{X} =79.60$
Example:7.निम्नलिखित सारणी एक माह के सप्ताहों के विभिन्न दिनों में हुई दुर्घटनाओं का विवरण प्रदर्शित करती है।औसत दुर्घटना प्रतिदिन का परिकलन कीजिए:
(The following table gives distribution of 100 accidents during seven days of the week of a month, calculate average accident per day):

$\begin{array}{ |p{2cm}|p{4cm}|} \hline Days & No of matches Accidents \\ \hline Sunday & 26 \\ Monday & 16 \\ Tuesday & 12 \\ Wednesday & 10 \\ Thrusday & 8\\ Friday & 10 \\ Saturday & 18 \\ \hline \end{array}$
इस माह में सोम,मंगल व बुधवार पाँच-पाँच तथा शेष चार दिवस चार-चार थे।
(During a particular month there were 5 Mondays,Tuesdays and Wednesdays and for each of the remaining four days.)
Solution:Calculation of Arithmetic Mean by Direct Method

$\begin{array}{ |p{2cm}|p{1cm}|p{3cm}|p{1cm}|} \hline Days & (f) & No of matches Accidents(X) & fx \\ \hline Sunday & 4 & 26 & 104 \\ Monday & 5 & 16 & 80 \\ Tuesday & 5 & 12 & 60 \\ Wednesday & 5 & 10 & 50 \\ Thrusday & 4 & 8 & 32 \\ Friday & 4 &10 & 40 \\ Saturday & 4 & 18 & 72 \\ \hline Total & 31 & & 438 \\ \hline \end{array} \\ \overline{X}=\frac{\Sigma f x}{\Sigma f} \\ =\frac{438}{31} \\ =14.129 \\ \overline{X} \approx \text{14.13 Accident per day}$
Example:8.निम्नलिखित समंक एक औद्योगिक संस्था द्वारा क्रय किये गये कोल से सम्बन्धित हैं।सरल एवं भारित समान्तर माध्य का परिकलन कीजिए:
(The following data relate to purchase of coal made by an industry calculate simple and weighted arithmetic means):

$\begin{array}{ |p{2cm}|p{3cm}|p{3cm}|} \hline Months & price per Qnt(Rs.) & Quintal purchased \\ \hline Jan. & 40.50 & 20 \\ Feb & 45.00 & 30 \\ March & 50.00 & 45 \\ April & 52.00 & 50 \\ May & 44.25 & 10 \\ June & 54.25 & 45 \\\hline Total & 31 & 438 \\ \hline \end{array}$
Solution:Calculation of Arithmetic Mean by Direct Method

$\begin{array}{ |p{2cm}|p{3cm}|p{2cm}|p{2cm}|} \hline Months & price per Qnt(Rs.) (X) & Quintal purchased & wx \\ \hline Jan. & 40.50 & 20 & 810 \\ Feb & 45.00 & 30 & 1350 \\ March & 50.00 & 45 & 2250 \\ April & 52.00 & 50 & 2600 \\ May & 44.25 & 10 & 442.5 \\ June & 54.25 & 45 & 2441.25 \\\hline Total & 286 & 200 & 9893.75 \\ \hline \end{array} \\ \overline{X}=\frac{\Sigma X}{N} \\ =\frac{286}{6} \\=47.666 \\ \Rightarrow \overline{X} \approx 47.67 \\ \overline{X}_{w}=\frac{\Sigma W X}{\Sigma W} \\ =\frac{9893.75}{200} \\=49.46875 \\ \overline{X}_{w} \approx 49.47$
Example:9.निम्नलिखित समंकों से समान्तर माध्य का परिकलन कीजिए:
(Calculate mean from the following data) :

$\begin{array}{ |p{2cm}|p{2cm}|} \hline S. No. & (f) \\ \hline 0-10 & 10 \\ 10-20 & 12 \\ 20-30 & 25 \\ 30-40 & 35 \\ 40-50 & 45 \\ 50-60 & 55 \\ 60-70 & 65 \\ \hline \text{Total} & 520 \\ \hline \end{array}$
Solution:Calculation of Arithmetic Mean by Short-cut Method

$\begin{array}{ |p{2cm}|p{2cm}|p{1cm}|p{3cm}|p{2cm}|} \hline S. No. & Mid value & (f) & Deviations from A=35(dx=X-A) & fdx \\ \hline 0-10 & 5 & 10 & -30 & -300 \\ 10-20 & 15 & 12 & -20 & -240 \\ 20-30 & 25 & 25 & -10 & -250 \\ 30-40& 35 & 35 &0 & 0\\ 40-50& 45 & 45 & 10 & 450 \\ 50-60& 55 & 55 & 20 & 1100 \\ 60-70 & 65 & 65 & 30 & 1950 \\ \hline \text{Total} &247 & & &2710\\ \hline \end{array} \\ \overline{X}=A+\frac{\Sigma f d x}{\Sigma f} \\ =35+\frac{2710}{247} \\ =35+10.9716 \\=45.9716 \\ \overline{X} \approx 45.97$
Example:10.निम्नलिखित समंकों से समान्तर माध्य का परिकलन कीजिए:
(Calculate mean of the following data):

$\begin{array}{ |p{3cm}|p{3cm}|} \hline Marks Below & No. of students \\ \hline 10 & 15 \\ 20 & 35 \\ 30 & 60 \\ 40 & 84 \\ 50 & 96 \\ 60 & 127 \\ 70 & 198 \\ 80 & 250 \\ \hline \end{array}$
Solution:Calculation of Arithmetic Mean by Short-cut Method

$\begin{array}{ |p{3cm}|p{3cm}|p{3cm}|p{3cm}|p{3cm}|} \hline Marks Below & Mid value & No. of students(f) & Deviations From A=35(dx=X-A) & fdx \\ \hline 0-10 & 5 & 15 & -30 & -450 \\ 10-20 & 15 & 20 & -20 & -400 \\ 20-30 & 25 & 25 &-10 & -250 \\ 30-40 & 35 & 24 & 0 & 0 \\ 40-50 & 45 & 12 & 10 & 120 \\ 50-60 & 55 & 31 & 20 & 620 \\ 60-70 & 65 & 71 & 30 & 2130 \\ 70-80 & 75 & 52 & 40 & 2080 \\ \hline \text{Total} & & 250 & & 3850 \\ \hline \end{array} \\ \overline{X}=A+\frac{\Sigma f dx}{\Sigma f} \\ =35+\frac{3850}{250}=35+154 \\ \Rightarrow \overline{X}=50.4 \text { Marks }$
उपर्युक्त उदाहरणों के द्वारा सांख्यिकी में माध्य (Mean in Statistics),सांख्यिकीय माध्य (Statistical Mean) को समझ सकते हैं।

3.सांख्यिकी में माध्य के सवाल (Mean in Statistics Questions):

Mean in Statistics

(1.)निम्न सूचना के आधार पर,श्रमिकों की औसत मजदूरी ज्ञात कीजिए:
(The following information relates to wage-groups of workers in a factory, their total working hours and the average working hours per worker.Calculate the wage per worker):

$\begin{array}{ |p{2cm}|p{2cm}|p{4cm}|} \hline Wages(Rs.) & Total Hours & Average Hours per Worker \\ \hline 35-45 & 88 & 8 \\ 45-55 & 185 & 7.4 \\ 55-65 & 273 & 7 \\ 65-75 & 162 & 9 \\ 75-85 & 70 & 10 \\ \hline \end{array}$
(2.)निम्न समंकों के समान्तर माध्य ज्ञात कीजिए:
(Calculate arithmetic mean from the following data):

$\begin{array}{ |p{2cm}|p{2cm}|} \hline Temperature & No. of Days \\ \hline -40 to -30 & 10 \\ -30 to -20 & 28 \\ -20 to -10 & 30 \\ -10 to 0 & 42 \\ 0-10 & 65 \\ 10-20 & 180 \\ 20-30 & 10 \\ \hline \end{array}$
उत्तर (Answers):(1.)58.50 (2.)4.29°c
उपर्युक्त सवालों को हल करने पर सांख्यिकी में माध्य (Mean in Statistics),सांख्यिकीय माध्य (Statistical Mean) को ठीक से समझ सकते हैं।

Also Read This Article:-Regression Equations by Least Squares

4.सांख्यिकी में माध्य (Frequently Asked Questions Related to Mean in Statistics),सांख्यिकीय माध्य (Statistical Mean) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:

प्रश्न:1.केन्द्रीय प्रवृत्ति के माप से क्या आशय है? (What Do You Mean by Measures of Central Tendency?):

उत्तर:एक समंक श्रेणी की केंद्रीय प्रवृत्ति का आशय उस समंक श्रेणी के अधिकांश मूल्यों की किसी एक मूल्य के आसपास केंद्रित होने की प्रवृत्ति से है जिसे मापा जा सके और इस प्रवृत्ति के माप को ही माध्य कहते हैं।माध्य को केंद्रीय प्रवृत्ति का माप इसलिए कहा जाता है क्योंकि व्यक्तिगत चर मूल्यों का जमाव अधिकतर उसी के आसपास होता है।इस प्रकार माध्य संपूर्ण समंक श्रेणी का एक प्रतिनिधि मूल्य होता है और इसलिए इसका स्थान सामान्यतः श्रेणी के मध्य में ही होता है।

प्रश्न:2.समान्तर माध्य की परिभाषा दीजिए। (Define Arithmetic Mean):

उत्तर:यूल व केण्डाल (Yule and Kendall) के शब्दों में, “किसी आवृत्ति वितरण की अवस्थिति या स्थिति के माप माध्य कहलाते हैं।”
काॅक्सटन एवं काउडेन (Croxten and Cowdon) के अनुसार, “माध्य समंकों के विस्तार के अन्तर्गत स्थित एक ऐसा मूल्य है जिसका प्रयोग श्रेणी का प्रतिनिधित्व करने के लिए किया जाता है।समंक श्रेणी के विस्तार के मध्य में स्थित होने के कारण ही माध्य को केन्द्रीय प्रवृत्ति का माप भी कहा जाता है।”
इसी प्रकार ए. ई. वाॅ (A. E. Waugh) के अनुसार” माध्य मूल्यों के एक समूह से चयन किया गया वह मूल्य है जो उनका किसी रूप में प्रतिनिधित्व करता है-एक ऐसा मूल्य जो पूर्ण समूह के लिए समूहों के मूल्यों के प्रतिरूप में है जिसका कि वह एक अंश है।”
सांख्यिकी के माध्य को महत्त्व देते हुए डाॅ. बाउले (Dr. Bowley) ने स्पष्ट किया है:”सांख्यिकी को वास्तव में माध्यों का विज्ञान कहा जा सकता है।”

प्रश्न:3.सांख्यिकी माध्य के दो उद्देश्य बताइए। (State Two Objects of Statistical Averages):

उत्तर:केन्द्रीय प्रवृत्ति के उद्देश्य एवं कार्य निम्न प्रकार हैं:
(1.)सामग्री को संक्षिप्त रूप में प्रस्तुत करना (To Present Collected Data in Brief):माध्य द्वारा हम संग्रहीत सामग्री को संक्षेप में प्रस्तुत करते हैं जिसे एक सामान्य व्यक्ति शीघ्रता व सरलता से समझकर स्मरण रख सकता है।उदाहरणार्थ,किसी देश के निवासियों में से प्रत्येक की आय पृथक-पृथक याद रखना असंभव है लेकिन उनकी प्रति व्यक्ति औसत आय का अंक याद रखा जा सकता है।
(2.)तुलनात्मक अध्ययन (Comparative Study):माध्यों का प्रयोग दो या दो से अधिक समूह के सम्बन्ध में सूचना देने के लिए किया जाता है।उस सूचना के आधार पर उन समूहों का पारस्परिक तुलनात्मक अध्ययन सरलता से कर सकते हैं।यदि उन दो समूहों से संबंधित समंक संग्रहीत किए जाएं तो कोई निश्चित परिणाम नहीं निकाल सकते।उदाहरणार्थ,हम दो कक्षाओं के छात्रों की आर्थिक स्थिति का पता केवल उन सभी की आय सम्बन्धी आँकड़ों के ज्ञात होने मात्र से ही नहीं कर सकते।यदि हम यह जानना चाहते हैं कि किस कक्षा के छात्रों की आर्थिक स्थिति अच्छी है तो उनकी औसत आय के आधार पर सरलता से उनका तुलनात्मक अध्ययन किया जा सकता है।
उपर्युक्त प्रश्नों के उत्तर द्वारा सांख्यिकी में माध्य (Mean in Statistics),सांख्यिकीय माध्य (Statistical Mean) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Instagram	click here
4.	Linkedin	click here
5.	Facebook Page	click here
6.	Twitter	click here

Mean in Statistics

सांख्यिकी में माध्य (Mean in Statistics)

Mean in Statistics

About Author

Satyam

About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.