Maxima and Minima in Class 12
1.कक्षा 12 में उच्चतम और निम्नतम (Maxima and Minima in Class 12),उच्चतम और निम्नतम कक्षा 12 (Maxima and Minima Class 12):
कक्षा 12 में उच्चतम और निम्नतम (Maxima and Minima in Class 12) के इस आर्टिकल में द्वितीय अवकलज परीक्षण द्वारा कुछ व्यावहारिक उदाहरणों के उच्चतम और निम्नतम ज्ञात करने का अध्ययन करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Maxima and Minima Class 12
2.कक्षा 12 में उच्चतम और निम्नतम पर आधारित उदाहरण (Examples Based on Maxima and Minima in Class 12):
Example:19.सिद्ध कीजिए कि एक दिए वृत्त के अन्तर्गत सभी आयतों में वर्ग का क्षेत्रफल उच्चतम होता है।
Solution:माना आयत ABCD एक वृत्त के अन्दर बना है जिसकी भुजाएँ x तथा y हैं।वृत्त का केन्द्र O तथा त्रिज्या a है।
समकोण त्रिभुज BCD में
x^2+y^2=4 a^2 \Rightarrow y=\sqrt{4 a^2-x^2} \ldots(1)
आयत का क्षेत्रफल=लम्बाई × चौड़ाई=xy
A=x \sqrt{4 a^2-x^2} \\ \Rightarrow A^2 =x^2\left(4 a^2-x^2\right)
माना S=A^2=4 a^2 x^2-x^4
x के सापेक्ष अवकलन करने परः
\frac{dS}{d x}=8 a^2 x-4 x^3 \ldots(2)
उच्चतम तथा निम्नतम के लिएः
\frac{dS}{dx} =0 \\ \Rightarrow 8 a^2 x-4 x^3=0 \\ \Rightarrow 4 x\left(2 a^2-x^2\right)=0 \\ \Rightarrow 2 a^2-x^2=0 \\ \Rightarrow x=\sqrt{2} a
समीकरण (2) का पुनः x के सापेक्ष अवकलन करने परः
\frac{d^2 S}{d x^2}=8 a^2-12 x^2 \\ x=\sqrt{2} a रखने परः
\frac{d^2S}{d x^2}=8 a^2-12(\sqrt{2} a)^2 \\ \Rightarrow 8 a^2-24 a^2 \\ \Rightarrow \frac{d^2 S}{d x^2}=-16 a^2<0
अतः x=\sqrt{2} a पर उच्चतम है।
x का मान समीकरण (1) में रखने परः
y=\sqrt{4 a^2-(\sqrt{2} a)^2} \\ \Rightarrow y=\sqrt{4 a^2-2 a^2} \\ \Rightarrow y=\sqrt{2} a
अतः x=y=\sqrt{2} a
उच्चतम क्षेत्रफल पर आयत एक वर्ग है।
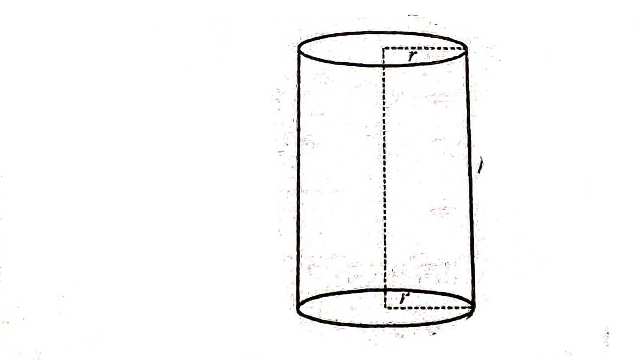
Example:20.सिद्ध कीजिए कि प्रदत्त पृष्ठ एवं महत्तम आयतन के बेलन की ऊँचाई,आधार के व्यास के बराबर होती है।
Solution:माना बेलन की त्रिज्या r तथा ऊँचाई h है।
अतः बेलन का सम्पूर्ण पृष्ठीय क्षेत्रफल
S=2 \pi r h+2 \pi r^2 \\ \Rightarrow \quad 2 \pi r h=S-2 \pi r^2 \\ \Rightarrow h =\frac{S}{2 \pi r}-r \ldots(1)
बेलन का आयतन V=\pi r^2 h \\ =\pi r^2\left(\frac{S}{2 \pi r}-r\right) \\ V=\frac{S r}{2}-\pi r^3 \ldots(2)
r के सापेक्ष अवकलन करने परः
\frac{d V}{d r}=\frac{S}{2}-3 \pi r^2 \ldots(3)
उच्चतम तथा निम्नतम के लिएः
\frac{d V}{d r}=0 \\ \Rightarrow \frac{S}{2}-3 \pi r^2=0 \Rightarrow 3 \pi r^2=\frac{S}{2} \\ \Rightarrow r =\sqrt{\frac{S}{6 \pi}} \ldots(4)
पुनः समीकरण (3) का r के सापेक्ष अवकलन करने परः
\frac{d^2 V}{dr^2}=-6 \pi r \\ r=\sqrt{\frac{S}{6 \pi}} रखने परः
\Rightarrow \frac{d^2 V}{d r^2}=-6 \pi \times \sqrt{\frac{S}{6 \pi}} \\ \Rightarrow \frac{d^2 V}{dr^2}=-\sqrt{6 \pi S}<0
अतः r=\sqrt{\frac{S}{6 \pi}} पर आयतन उच्चतम है।
S का मान समीकरण (1) में रखने परः
h=\frac{\left(6 \pi r^2\right)}{2 \pi r}-r \Rightarrow h=2 r
बेलन की ऊँचाई (h)=2r=आधार का व्यास
फलतः जब बेलन की ऊँचाई आधार के व्यास के बराबर होगी तो बेलन का आयतन महत्तम होगा।
Example:21.100 घनसेमी आयतन वाले डिब्बे सभी बन्द बेलनाकार (लम्ब वृत्तीय) डिब्बों में से न्यूनतम पृष्ठ क्षेत्रफल वाले डिब्बे की विमाएँ ज्ञात कीजिए।
Solution:माना बेलनाकार डिब्बों की त्रिज्या तथा ऊँचाई क्रमशः r तथा h है।
बेलन का आयतन V=\pi r^2 h=100 \\ \Rightarrow h=\frac{100}{\pi r^2} \ldots(1)
बेलनाकार डिब्बों का सम्पूर्ण पृष्ठीय क्षेत्रफल
S=2 \pi r h+2 \pi r^2
समीकरण (1) से h का मान रखने परः
S=2 \pi r \times \frac{100}{\pi r^2}+2 \pi r^2 \\ \Rightarrow S=\frac{200}{r}+2 \pi r^2
r के सापेक्ष अवकलन करने परः
\frac{dS}{dr}=-\frac{200}{r^2}+4 \pi r \ldots(2)
अधिकतम तथा न्यूनतम के लिए
\frac{dS}{dr}=0 \\ -\frac{200}{r^2}+4 \pi r=0 \\ \Rightarrow r^3=\frac{200}{4 \pi} \\ \Rightarrow r^3=\frac{50}{\pi} \\ \Rightarrow r=\left(\frac{50}{\pi}\right)^{\frac{1}{3}} \ldots(3)
समीकरण (2) का पुनः r के सापेक्ष अवकलन करने परः
\frac{d^{2}S}{d r^2}=\frac{400}{r^3}+4 \pi \\ r^3=\frac{50}{\pi} रखने परः
अतः r^3=\frac{50}{\pi} पर बेलनाकार डिब्बों के पृष्ठ क्षेत्रफल न्यूनतम होंगे।
समीकरण (1) में r का मान रखने परः
h=\frac{100}{\pi\left[\left(\frac{50}{\pi}\right)^{\frac{1}{3}}\right]^2} \times \left( \frac{\pi}{50} \right)^{\frac{2}{3}} \\ \Rightarrow h=2\left(\frac{50}{\pi}\right)^{\frac{1}{3}}
अतः बेलनाकार डिब्बों की विमाएँ r=\left(\frac{50}{\pi}\right)^{\frac{1}{3}}, h=2\left(\frac{50}{\pi} \right)^{\frac{1}{3}}
Example:22.एक 28cm लम्बे तार को दो टुकड़ों में विभक्त किया जाना है।एक टुकड़े से वर्ग तथा दूसरे से वृत्त बनाया जाना है।दोनों टुकड़ों की लम्बाई कितनी होनी चाहिए जिससे वर्ग एवं वृत्त का सम्मिलित क्षेत्रफल न्यूनतम हो?
Solution:माना तार के एक भाग की लम्बाई x है जिससे वर्ग बनाया जाना है तथा दूसरे भाग की लम्बाई 28-x है जिससे वृत्त बनाया जाना है।
वर्ग का परिमाप=x
वर्ग की भुजा=\frac{x}{4}
वर्ग का क्षेत्रफल \left(A_1\right)=\frac{x^2}{16}
वृत्त की परिधि 2 \pi r=28-x
वृत्त की त्रिज्या r=\frac{28-x}{2 \pi}
वृत्त का क्षेत्रफल A_2=\pi r^2 \\ \Rightarrow A_2=\pi \times\left(\frac{28-x}{2 \pi}\right)^2 \\ \Rightarrow A_2=\frac{(28-x)^2}{4 \pi}
वर्ग तथा वृत्त का सम्मिलित क्षेत्रफल
A =A_1+A_2 \\ A =\frac{x^2}{16}+\frac{(28-2)^2}{4 \pi} \cdots(1)
x के सापेक्ष अवकलन करने परः
\frac{d A}{d x}=\frac{x}{8}-\frac{(28-x)}{2 \pi} \quad \ldots(2)
उच्चतम तथा निम्नतम के लिएः
\frac{x}{8}-\frac{28-x}{2 \pi}=0 \\ \Rightarrow 2 \pi x=224-8 x \\ \Rightarrow 2 \pi x+8 x=224 \\ \Rightarrow x(2 \pi+8)=224 \\ \Rightarrow x=\frac{224}{2(\pi+4)} \\ \Rightarrow x=\frac{112}{\pi+4}
समीकरण (2) का पुनः x के सापेक्ष अवकलन करने परः
\frac{d^2 A}{d x^2}=\frac{1}{8}+\frac{1}{2 \pi}=\frac{\pi+4}{8 \pi}>0
अतः सम्मिलित क्षेत्रफल न्यूनतम होगा।
तार के एक भाग की लम्बाई=\frac{112}{\pi+4}
तार के दूसरे भाग की लम्बाई=28-x=28-\frac{112}{\pi+4}=\frac{28}{\pi+4}
Example:23.सिद्ध कीजिए कि R त्रिज्या के गोले के अन्तर्गत विशालतम शंकु का आयतन,गोले के आयतन का \frac{8}{27} होता है।
Solution:माना R त्रिज्या के गोले में ABC शंकु बना है।O गोले का केन्द्र है।
OA=OB=OQ=R (गोले की त्रिज्या)
माना BP=x
समकोण \triangle OBP में
OP^2=OB^2-BP^2 \\ =R^2-x^2 \\ \Rightarrow OP=\sqrt{R^2-x^2}
शंकु की ऊँचाई AP=AO+OP
\Rightarrow h=R+\sqrt{R^2-x^2}
शंकु की त्रिज्या r=BP=x
शंकु का आयतन V=\frac{1}{3} \pi r^2 h \\ =\frac{1}{3} \pi x^2\left(R+\sqrt{R^2-x^2}\right) \\ V=\frac{\pi}{3}\left(R x^2+x^2 \sqrt{R^2-x^2}\right)
x के सापेक्ष अवकलन करने परः
\frac{dV}{dx}=\frac{\pi}{3}\left(2 R x+2 x \sqrt{R^2-x^2}-\frac{x^3}{\sqrt{R^2-x^2}}\right) \ldots(1)
अधिकतम आयतन के लिएः
\frac{dV}{dx}=0 \\ \frac{\pi}{3}\left(2 R x+2 x \sqrt{R^2-x^2}-\frac{x^3}{\sqrt{R^2-x^2}}\right)=0 \\ \Rightarrow 2 R+2 \sqrt{R^2-x^2}=\frac{x^2}{\sqrt{R^2-x^2}} \\ \Rightarrow 2 R \sqrt{R^2-x^2}+ 2\left( R^2-x^2\right)=x^2 \\ \Rightarrow 2 R \sqrt{R^2-x^2}=x^2-2 R^2+2 x^2 \\ \Rightarrow 2 R \sqrt{R^2-x^2}=3 x^2-2 R^2 \\ \Rightarrow 4 R^2\left(R^2-x^2\right)=9 x^4-12 R^2 x^2+4 R^4 \\ \Rightarrow 9 x^4-8 R^2 x^2=0 \\ \Rightarrow 9 x^2-8 R^2=0 \\ \Rightarrow x=\frac{2 \sqrt{2}}{3} R
समीकरण (1) का पुनः x के सापेक्ष अवकलन करने परः
\frac{d^2 V}{d x^2}=\frac{\pi}{3}\left(2 R+2 \sqrt{R^2-2 x^2}-\frac{2 x^2}{\sqrt{R^2-x^2}}-\frac{\left(\sqrt{R^2-x^2} \cdot 3 x^2-\frac{x^3 \cdot(-x)}{\sqrt{R^2-x^2}}\right)}{R^{2}-x^{2}}\right) \\ =\frac{\pi}{3}\left[ 2R + 2 \sqrt { R^{2}-x^{2}} - \frac { 2 x^{2}} {\sqrt {R^{2}-x^{2}} } - \frac{(3x^{2} R ^{2}-2x^{4})}{\left( R^{2}-x^{2}\right)^{\frac{3}{2}} }\right] \\ x=\frac{2 \sqrt{2}}{3} R रखने परः
\frac{d^2 V}{d x^2}=\frac{\pi}{3}\left[2 R+2 \sqrt{R^2-\frac{8}{9} R^2}-\frac{2 \times \frac{8}{9} R^2}{\sqrt{R^2-\frac{8}{9} R^2}}\right. -\left(\frac{3 R^2 \times \frac{8}{9} R^2-2 \times \frac{64}{81} R^4}{\left(R^2-\frac{8}{9} R^2\right)^{\frac{3}{2}}}\right] \\ \frac{d^2 V}{d x^2}=\frac{\pi}{3}\left[2 R+\frac{2 R}{3}-\frac{16}{9} R^2 \times \frac{3}{R}-\frac{\left(\frac{8 R^4}{3}-\frac{128}{81} R^4\right)}{\frac{R^3}{27}} \right] \\ =\frac{\pi}{3}\left[\frac{8 R}{3}-\frac{16}{3} R-\frac{88 R^4}{81} \times \frac{27}{R^3}\right] \\ =\frac{\pi}{3}\left[-\frac{8 R}{3}-\frac{88}{3} R\right] \\ \Rightarrow \frac{d^2 V}{d x^2}=-\frac{96 \pi R}{9}<0
अतः शंकु का आयतन महत्तम होगा जब
x=\frac{2 \sqrt{2}}{3} R
शंकु की ऊँचाई =R+\sqrt{R^2-x^2} \\ =R+\sqrt{R^2-\frac{8 R^2}{9}}=R+\frac{R}{3} \\ \Rightarrow h=\frac{4 R}{3}
शंकु की त्रिज्या (r)=x=\frac{2 \sqrt{2}}{3} R
शंकु का आयतन V= \frac{\pi}{3} \times\left(\frac{2 \sqrt{2}}{3} R\right)^2 \times \frac{4 R}{3} \\ =\frac{\pi}{3} \times \frac{8}{9} R^2 \times \frac{4 R}{3} \\ \Rightarrow V =\frac{32}{81} R^2 \pi \\ \Rightarrow V =\frac{8}{27}\left(\frac{4}{3} \pi R^3\right)
शंकु का आयतन (V)=\frac{8}{27} \times (गोले का आयतन)
Example:24.सिद्ध कीजिए कि न्यूनतम पृष्ठ का दिए आयतन के लम्ब वृत्तीय शंकु की ऊँचाई, आधार की त्रिज्या की \sqrt{2} गुनी होती है।
Solution:माना शंकु की त्रिज्या,ऊँचाई तथा आयतन क्रमशः r, h तथा V है।
शंकु का आयतन V=\frac{1}{3} \pi r^2 h \\ \Rightarrow h=\frac{3 V}{\pi r^2}
शंकु का वक्र पृष्ठीय क्षेत्रफल S=\pi r l \\ \Rightarrow S^2=\pi^2 r^2 l^2 \\ =\pi^2 r^2\left(h^2+r^2 \right)\left[\because l^2=h^2+r^2\right] \\ =\pi^2 r^2\left[\frac{9 V^2}{\pi^2 r^4}+r^2\right]
माना A=S^2=\frac{9 V^2}{r^2}+\pi^2 r^4
r के सापेक्ष अवकलन करने परः
\frac{d A}{d r}=\frac{-18 V^2}{r^3}+4 \pi^2 r^3 \ldots(1)
न्यूनतम तथा अधिकतम पृष्ठ के लिएः
\frac{d A}{d r}=0 \\ -\frac{18 V^2}{r^3}+4 \pi^2 r^3=0 \\ \Rightarrow 4 \pi^2 r^3=\frac{18 V^2}{r^3} तथा r=\left(\frac{9 V^2}{2 \pi^2}\right)^{\frac{1}{6}}
V का मान रखने परः
\Rightarrow 4 \pi^2 r^3=\frac{18}{r^3}\left(\frac{1}{9} \pi^2 r^4 h^2\right) \\ \Rightarrow 4 \pi^2 r^3=2 \pi^2 r h^2 \\ \Rightarrow h^2=2 r^2 \\ \Rightarrow h=\sqrt{2} r
समीकरण (1) का पुनः r के सापेक्ष अवकलन करने परः
\frac{d^2 A}{d r^2} =\frac{54 V^2}{r^4}+12 \pi^2 r^2 \\ =\frac{54 V^2}{\left(\frac{9 V^2}{2 \pi^2} \right)^{\frac{4}{6}}}+12 \pi^2\left(\frac{9 v^2}{2 \pi^2}\right)^{\frac{2}{6}} \\ \Rightarrow \frac{d^2 A}{d r^2} =54 V^2\left(\frac{2 \pi}{9 V^2}\right)^{\frac{2}{3}}+12 \pi^2\left(\frac{9 V^2}{2 \pi^2} \right)^{\frac{1}{3}} >0
अतः h=\sqrt{2}r के लिए वक्र पृष्ठीय क्षेत्रफल न्यूनतम है।
Example:25.सिद्ध कीजिए कि दी हुई तिर्यक ऊँचाई और महत्तम आयतन वाले शंकु का अर्धशीर्ष कोण \tan ^{-1} \sqrt{2} होता है।
Solution:माना शंकु की त्रिज्या तथा ऊँचाई क्रमशः r तथा h है।
तिर्यक ऊँचाई=l, शंकु का आयतन=V
ऊँचाई h=\sqrt{l^2-r^2}
शंकु का आयतन V=\frac{1}{3} \pi r^2 h \\ \Rightarrow V=\frac{1}{3} \pi r^2 \sqrt{l^2-r^2} \\ \Rightarrow V^2=\frac{1}{9} \pi^2 r^4\left(l^2-r^2\right)
माना T=V^2=\frac{1}{9} \pi^2 r^2 r^4-\frac{1}{9} \pi^2 r^6
r के सापेक्ष अवकलन करने परः
\frac{d T}{d r}=\frac{4}{9} \pi^2 l^2 r^3-\frac{2}{3} \pi^2 r^5 \cdots \text { (1) }
महत्तम तथा न्यूनतम के लिएः \frac{dT}{dr}=0 \\ \frac{4}{9} \pi^2 l^2 r^3-\frac{2}{3} \pi^2 r^5=0 \\ \Rightarrow \frac{2}{3} \pi^2 r^3\left(\frac{2}{3} l^2-r^2\right)=0 \\ \Rightarrow \frac{2}{2} l^2-r^2=0 \\ \Rightarrow r=\sqrt{\frac{2}{3}} l
पुनः समीकरण (1) का r के सापेक्ष अवकलन करने परः
\frac{d^2 T}{d r^2}=\frac{4}{3} \pi^2 l^2 r^2-\frac{10}{3} \pi^2 r^4 \\ r=\sqrt{\frac{2}{3}} l रखने परः
\frac{d^2 T}{d r^2}=\frac{4}{3} \pi^2 l^2\left(\frac{2}{3} l^2\right)-\frac{10}{3} \pi^2 \times \frac{4}{9} l^4 \\ =\frac{8}{9} \pi^2 l^4-\frac{40}{27} \pi^2 l^4 \\ =\frac{24 \pi^2 l^4-40 \pi^2 l^4}{27} \\ \Rightarrow \frac{d^2 T}{d r^2}=-\frac{16}{27} \pi^2 l^4<0
अतः r=\sqrt{\frac{2}{3}} l पर आयतन महत्तम है।
h=\sqrt{l^2-r^2} \\ \Rightarrow h =\sqrt{l^2-\frac{2}{3} l^2}=\sqrt{\frac{1}{3}} l
अर्धशीर्ष कोण हो तो \tan \theta=\frac{\text{ लम्ब }}{\text{ आधार }} \\ \Rightarrow \tan \theta=\frac{O B}{A O}=\frac{\sqrt{\frac{2}{3}} l}{\sqrt{\frac{1}{3}} l} \\ \Rightarrow \tan \theta =\sqrt{2} \\ \Rightarrow \theta=\tan ^{-1}(\sqrt{2})
Example:26.सिद्ध कीजिए कि दिए हुए पृष्ठ और महत्तम आयतन वाले लम्ब वृत्तीय शंकु का अर्धशीर्ष कोण \sin^{-1} \left( \frac{1}{3} \right) होता है।
Solution:माना शंकु की त्रिज्या=r
उर्ध्वाधर ऊँचाई=h
तिर्यक ऊँचाई=l
पृष्ठीय क्षेत्रफल=S
आयतन=V तथा अर्द्धशीर्ष कोण=\theta
समकोण \triangle AOC में
\sin \theta=\frac{r}{l} \Rightarrow r=l \sin \theta \\ \cos \theta=\frac{h}{l} \Rightarrow h=l \cos \theta
शंकु का पृष्ठीय क्षेत्रफल S=\pi rl + \pi r^{2} \\ S=\pi l^2 \sin \theta+\pi l^2 \sin ^2 \theta \\ \Rightarrow l^2=\frac{S}{\pi \sin \theta(1+\sin \theta)} \\ \Rightarrow l=\frac{S^{\frac{1}{2}}}{\pi^{\frac{1}{2}} \sin ^{\frac{1}{2}} \theta(1+\sin \theta)^{\frac{1}{2}}}
शंकु का आयतन V=\frac{1}{3} \pi r^2 h \\ =\frac{1}{3} \pi l^2 \sin ^2 \theta l \cos \theta \\ V=\frac{1}{3} \pi l^3 \sin ^2 \theta \cos \theta \\ l^{3} का मान रखने परः
V=\frac{1}{3} \pi \frac{S^{\frac{3}{2}} \sin^{2} \theta \cos \theta}{\pi^{3} \sin ^{3} \theta(1+\sin \theta)^{3}}
वर्ग करने परः
V^2=\frac{1}{9} \pi^2 \frac{S^3 \cdot \sin ^4 \theta \cos ^2 \theta}{\pi^3 \sin ^3 \theta(1+\sin \theta)^3}
माना P=V^2=\frac{S^3}{9 \pi} \frac{\sin \theta \cos ^2 \theta}{(1+\sin \theta)^3} \\ \theta के सापेक्ष अवकलन करने परः
\frac{dP}{d \theta}=\frac{S^3}{9 \pi}\left[\frac{(1+\sin \theta)^3\left(\cos ^3 \theta-2 \sin ^2 \theta \cos \theta\right)-3(1+\sin \theta)^2 \cdot \sin \theta \cos ^3 \theta}{(1+\sin \theta)^6}\right] \\ =\frac{S^3}{9 \pi}\left[\frac{(1+\sin \theta)\left(\cos ^3 \theta-2 \sin^{2} \theta \cos \theta\right)-3 \sin \theta \cos ^3 \theta}{(1+\sin \theta)^{4}}\right] \\ =\frac{S^3}{9 \pi}\left[\frac{\cos ^3 \theta+\sin \theta \cos^{3} \theta-2 \sin^{2} \theta \cos \theta-2 \sin ^{3} \theta \cos \theta-3 \sin \theta \cos ^3 \theta}{(1+\sin \theta)^{4}}\right] \\ =\frac{S^3}{9 \pi} \left [ \frac{\cos ^3 \theta-2 \sin \theta \cos ^3 \theta-2 \sin ^2 \theta \cos \theta -2 \sin^{3} \theta \cos \theta-3 \sin \theta \cos^{3} \theta}{(1+\sin \theta)^{4}} \right] \\ \Rightarrow \frac{d P}{d \theta}=\frac{S^3}{9 \pi}\left[\frac{\cos ^3 \theta-2 \sin \theta \cos ^3 \theta-2 \sin ^2 \theta \cos \theta-2 \sin ^3 \theta \sin \theta}{(1+\sin \theta)^4}\right]
न्यूनतम तथा महत्तम के लिएः
\frac{S^3}{9 \pi}\left[\frac{\cos ^3 \theta-2 \sin \theta \cos ^3 \theta-2 \sin ^2 \theta \cos \theta-2 \sin ^3 \theta \sin \theta}{(1+\sin \theta)^4}\right]=0 \\ \Rightarrow \cos ^2 \theta-2 \sin \theta \cos ^2 \theta-2 \sin ^2 \theta-2 \sin ^3 \theta=0\\ \Rightarrow 1-\sin ^2 \theta-2 \sin \theta+2 \sin ^3 \theta-2 \sin ^2 \theta-2 \sin ^3 \theta=0 \\ \Rightarrow 1-2 \sin \theta-3 \sin ^2 \theta=0 \\ \Rightarrow 1-3 \sin \theta+\sin \theta-3 \sin ^2 \theta=0 \\ \Rightarrow 1(1-3 \sin \theta)+\sin \theta(1-3 \sin \theta)=0 \\ \Rightarrow(1+\sin \theta)(1-3 \sin \theta)=0 \\ \sin \theta=-1,\frac{1}{3} \\ \sin \theta=\sin \frac{3\pi}{2}, \theta=\sin ^{-1}\left(\frac{1}{3} \right) अर्थात् \sin \theta=\frac{1}{3} \\ \theta=\frac{3\pi}{2} (असंभव है) अतः \sin \theta=\frac{1}{3} \\ \cos \theta=\frac{\sqrt{8}}{3}
समीकरण (1) का पुनः \theta के सापेक्ष अवकलन करने परः
\frac{d^2 P}{d \theta^2}=\frac{S^3}{9 \pi} \frac{\left[\begin{matrix} (1+\sin \theta)^4-(3 \cos ^2 \theta \sin \theta-2 \cos ^4 \theta +6 \sin ^2 \theta \cos ^2 \theta\\-4 \sin \theta \cos ^2 \theta +2 \sin ^3 \theta-6 \sin ^2 \theta \cos ^2 \theta +2 \sin ^4 \theta) -(-2 \sin^{2} \theta \cos \theta\\+\cos^{3} \theta-2 \sin \theta \cos^{3} \theta -2 \sin^{3} \theta \cos \theta)4 (1+\sin \theta)^{3} \cos \theta \end{matrix}\right]}{(1+\sin \theta)^{8}} \\ =\frac{S^3}{9 \pi} \frac{\left[\begin{matrix}-7 \cos^2 \theta \sin \theta+2 \sin ^3 \theta-2 \cos ^4 \theta +2 \sin ^4 \theta-7 \cos ^2 \theta \sin ^2 \theta\\+ 2 \sin ^4 \theta-2 \cos ^4 \theta \sin \theta+2 \sin ^5 \theta -4 \cos ^4 \theta+8 \sin \theta \cos ^4 \theta \\+8 \sin ^2 \theta \cos ^2 \theta +8 \sin ^3 \theta \cos ^2 \theta\end{matrix}\right]}{(1+\sin \theta)^5}\\ =\frac{S^3}{9 \pi} \frac{-7 \cos ^2 \theta \sin \theta+2 \sin ^3 \theta-6 \cos ^4 \theta +4 \sin ^4 \theta+\sin ^2 \theta \cos ^2 \theta+6 \sin \theta \cos^{4} \theta +2 \sin ^5 \theta+8 \sin ^3 \theta \cos ^2 \theta}{(1+\sin \theta)^5} \\ \sin \theta व \cos \theta का मान रखने परः
\frac{d^2 P}{d \theta^2}=\frac{S^3}{9 \pi} \left[\frac{-7 \times \frac{8}{9} \times \frac{1}{3}+2 \times \frac{1}{27}-6 \times \frac{64}{81}+4 \times \frac{1}{81}+\frac{1}{9} \times \frac{8}{9} +6 \times \frac{1}{3} \times \frac{64}{81}+\frac{2}{243}+8 \times \frac{1}{27} \times \frac{8}{9} }{(1+\frac{1}{3})^5}\right] \\ = \frac{S^3}{9 \pi} \left[\frac{\frac{-56}{27}+\frac{2}{27}-\frac{128}{27}+\frac{4}{81}+\frac{8}{81}+\frac{128}{81}+\frac{2}{243}+\frac{64}{243}}{\left(\frac{1024}{243} \right)}\right] \\ =\frac{S^3}{9 \pi}\left[ \frac{(-504+18-1152+12+24+384+2+64)}{243}\right] \times \frac{243}{1024} \\ =\frac{S^3}{9 \pi}\left(-\frac{1152}{1024}\right) \\ \Rightarrow \frac{d^2 P}{d \theta^2}=-\frac{S^3}{8 \pi}<0
अतः अर्धशीर्ष कोण \theta=\sin ^{-1}\left(\frac{1}{3}\right) पर शंकु का आयतन महत्तम है।
प्रश्न संख्या 27 से 29 में सही उत्तर का चुनाव कीजिए।
Example:27.वक्र x^2=2 y पर (0,5) से न्यूनतम दूरी पर स्थित बिन्दु हैः
(A) (2 \sqrt{2},4) (B) (2 \sqrt{2},0) (C)(0,0) (D)(2,2)
Solution:माना बिन्दु A(x,y) वक्र x^2=2y पर है जो कि बिन्दु B(0,5) से न्यूनतम दूरी पर है।
AB=\sqrt{(x-0)^2+(y-5)^2} \\ \Rightarrow AB^2=x^2+(y-5)^2
माना D=A B^2=x^2+(y-5)^2 \ldots(1) \\ x^2=2 y \ldots(2)
(1) व (2) सेः
D=x^2+\left(\frac{x^2}{2}-5\right)^2 \\ \Rightarrow D=x^2+\frac{x^4}{4}-5 x^2+25 \\ D=\frac{x^4}{4}-4 x^2+25
x के सापेक्ष अवकलन करने परः
\frac{d D}{d x}=x^3-8 x \ldots(3)
न्यूनतम तथा अधिकतम के लिएः
\frac{dD}{dx}=0 \\ x^3-8 x=0 \\ \Rightarrow x\left(x^2-8\right)=0 \Rightarrow x=0,2 \sqrt{2}
समीकरण (3) का पुनः अवकलन करने परः
\frac{d^2 D}{d x^2}=3 x^2-8
x=0 पर \frac{d^2 D}{d x^2}=-8<0 महत्तम है।
x=2 \sqrt{2} पर \frac{d^2 D}{d x^2}=3(2 \sqrt{2})^2-8=16>0 \\ x=2 \sqrt{2} पर निम्नतम है।
समीकरण (2) में x=2 \sqrt{2} रखने परः (2 \sqrt{2})^2=2 y \\ \Rightarrow y=4
अतः वक्र से न्यूनतम दूरी पर बिन्दु हैः (2 \sqrt{2},4)
उत्तर (A) (2 \sqrt{2},4)
Example:28.x,के सभी वास्तविक मानों के लिए \frac{1-x+x^2}{1+x+x^2} न्यूनतम मान हैः
(A)0 (B) 1 (C)3 (D) \frac{1}{3}
Solution:माना y=\frac{1-x+x^2}{1+x+x^2}
x के सापेक्ष अवकलन करने परः
\frac{d y}{d x}=\frac{\left(-1+2 x\right) (1+x+x^{2})-(1+2 x)\left(1-x+x^2\right)}{\left(1+x+x^2\right)^2} \\ = \frac{-1-x+x^2+2 x+2 x^2+2 x^3-1+x-x^2-2 x+2 x^2-2 x^3}{\left(1+x+x^2\right)^{2}} \\ \frac{d y}{d x}=\frac{2 x^2-2}{\left(1+x+x^2\right)^2}
न्यूनतम के लिएः \frac{d y}{d x}=0 \\ \Rightarrow 2 x^2-2=0 \\ \Rightarrow x=\pm 1
x=1 पर y(1)=\frac{1-1+1^2}{1+1+1^2}=\frac{1}{3}
x=-1 पर y(-1)=\frac{1+1+(-1)^2}{1-1+(-1)^2}=3
अतः फलन का न्यूनतम मान=\frac{1}{3}
(D) \frac{1}{3}
Example:29. [x(x-1)+1]^{\frac{1}{3}}, 0 \leq x \leq 1 का उच्चतम मान हैः
(A)\left( \frac{1}{3} \right)^{\frac{1}{3}} (B) \frac{1}{2} (C)1 (D) 0
Solution:माना y=[x(x-1)+1]^{\frac{1}{3}} \\ y^3=\left(x^2-x+1\right)
माना P=x^2-x+1
x के सापेक्ष अवकलन करने परः
\frac{d P}{d x}=2 x-1
उच्चतम मान के लिएः \frac{d P}{d x}=0 \\ 2 x-1=0 \Rightarrow x=\frac{1}{2} \\ \because x \in [0,1] अथवा 0 \leq x \leq 1
x=0 के लिए y(0)=[0(0-1)+1]^{\frac{1}{3}}=1 \\ x=\frac{1}{2} के लिए y(1)=\left[\frac{1}{2}\left(\frac{1}{2}-1\right)+1\right]^{\frac{1}{3}}=\left(-\frac{1}{4}+1\right)^{\frac{1}{3}}=\left(\frac{3}{4}\right)^{\frac{1}{3}}
x=1 के लिए y(1)=[1(1-1)+1]^{\frac{1}{3}}=1
अतः फलन का उच्चतम मान 1 है।
(C)1 उत्तर
उपर्युक्त उदाहरणों के द्वारा कक्षा 12 में उच्चतम और निम्नतम (Maxima and Minima in Class 12),उच्चतम और निम्नतम कक्षा 12 (Maxima and Minima Class 12) को समझ सकते हैं।
3.कक्षा 12 में उच्चतम और निम्नतम के सवाल (Maxima and Minima in Class 12 Questions):
(1.)सिद्ध कीजिए कि त्रिज्या a के एक गोले से उत्कीर्ण अधिकतम आयतन वाले बेलन की ऊँचाई \left(\frac{2 a}{\sqrt{3}}\right) होगी।
(2.)एक नियत आयतन वाले खुले टैंक का आधार (पैंदा) वर्गाकार है।यदि अन्तःपृष्ठ न्यूनतम हो तो टैंक की गहराई तथा लम्बाई का अनुपात ज्ञात कीजिए।
उपर्युक्त सवालों को हल करने पर कक्षा 12 में उच्चतम और निम्नतम (Maxima and Minima in Class 12),उच्चतम और निम्नतम कक्षा 12 (Maxima and Minima Class 12) को ठीक से समझ सकते हैं।
Also Read This Article:-Minima and Maxima Class 12
4.कक्षा 12 में उच्चतम और निम्नतम (Frequently Asked Questions Related to Maxima and Minima in Class 12),उच्चतम और निम्नतम कक्षा 12 (Maxima and Minima Class 12) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्नः
प्रश्नः1.फलन के निरपेक्ष उच्चतम और निरपेक्ष निम्नतम मान किसे कहते हैं? (What are the Absolute Maximum and Absolute Minimum Values?):
उत्तरःस्थानीय उच्चतम या स्थानीय निम्नतम को क्रमशः निरपेक्ष उच्चतम या निरपेक्ष निम्नतम मान कहा जाता है।
प्रश्नः2.फलन के चरम मान किसे कहते हैं? (What is the Extreme Value of the Function?):
उत्तरःकिसी प्रान्त में फलन के उच्चिष्ठ एवं निम्निष्ठ मान एक से अधिक हो सकते हैं परन्तु प्रान्त में निरपेक्ष अधिकतम या निरपेक्ष न्यूनतम मान केवल एक ही होता है।एक उच्चिष्ठ मान,निम्निष्ठ मान से कम हो सकता है।इसी प्रकार एक निम्निष्ठ मान,उच्चिष्ठ मान से अधिक हो सकता है।फलन के उच्चिष्ठ एवं निम्निष्ठ मान को चरम मान भी कहते हैं।
प्रश्न:3.फलन के उच्चिष्ठ और निम्निष्ठ के गुणधर्म क्या हैं? (What are the Properties of the Maxima and Minima of the Function?):
उत्तरःयदि फलन f(x) संतत है तो फलन के उच्चिष्ठ और निम्निष्ठ में निम्न विशेषताएँ होती हैंः
(1.)फलन f(x) के दो समान मानों के मध्य कम से कम एक उच्चिष्ठ या निम्निष्ठ मान अवश्य होता है।
(2.)उच्चिष्ठ व निम्निष्ठ मान एकान्तर क्रम में विद्यमान होते हैं।
(3.)f'(x) का चिन्ह धन से ऋण होता है जब f(x) उच्चिष्ठ बिन्दु से गुजरता है तथा जब f'(x) का चिन्ह ऋण से धन होता है तो f(x) निम्निष्ठ बिन्दु से गुजरता है।
(4.)यदि किसी बिन्दु के दोनों तरफ f'(x) का चिन्ह नहीं बदलता है तो वह नति परिवर्तन बिन्दु होता है।
(5.)उच्चिष्ठ एवं निम्निष्ठ बिन्दु पर f'(x)=0 होने से उस बिन्दु पर स्पर्शरेखा x-अक्ष के समान्तर होती है।
(6.)यदि किसी बिन्दु पर f(x) का मान उच्चिष्ठ (निम्निष्ठ) हो तो उस बिन्दु \frac{1}{f(x)}[f(x) \neq 0] का मान निम्निष्ठ (उच्चिष्ठ) होता है।
उपर्युक्त प्रश्नों के उत्तर द्वारा कक्षा 12 में उच्चतम और निम्नतम (Maxima and Minima in Class 12),उच्चतम और निम्नतम कक्षा 12 (Maxima and Minima Class 12) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Maxima and Minima in Class 12
कक्षा 12 में उच्चतम और निम्नतम
(Maxima and Minima in Class 12)
Maxima and Minima in Class 12
कक्षा 12 में उच्चतम और निम्नतम (Maxima and Minima in Class 12) के इस आर्टिकल में द्वितीय
अवकलज परीक्षण द्वारा कुछ व्यावहारिक उदाहरणों के उच्चतम और निम्नतम ज्ञात करने का अध्ययन करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.