1.गणित:एक सुंदर बात बदसूरत बना दिया (Mathematics A Beautiful Thing Made Ugly),मैथमेटिक्स:ए ब्यूटीफुल थिंग मेड अग्ली (Mathematics: A Beautiful Thing Made Ugly):

• गणित:एक सुंदर बात बदसूरत बना दिया (Mathematics A Beautiful Thing Made Ugly) के द्वारा यह बताया गया है कि कैसे कुछ चीजों के कारण गणित को बदसूरत बना दिया गया है.सोशल मीडिया भी इससे अप्रभावित नहीं है। सोशल मीडिया गणित की सुन्दरता को भुला बैठा है। सोशल मीडिया पर अक्सर गणित की पहेलियाँ या कुछ इसी तरह की बातें पोस्ट की जाती हैं।सोशल मीडिया एवं इंटरनेट ने ऐसा करके गणित के लिए समस्या पैदा कर दी है क्योंकि अच्छी, सुन्दर और दिलचस्प गणित को बढ़ावा देने के लिए कई साइटें काम कर रही है परन्तु उनका अक्सर ही कहीं जिक् होता है।इस प्रकार का खिलवाड़ नहीं किया जाना चाहिए।
• गणित को आधुनिक युग में हर क्षेत्र में विस्तार हुआ है और यह स्वयंसिद्ध पर आधारित है परन्तु इसके प्रचार-प्रसार और जनमानस तक पहुंचाने की आवश्यकता है।
• इंटरनेट और सोशल मीडिया गणितीय पहेलियों और तार्किक समस्याओं को प्रकाशित करने और उनका हल करने के साथ ही समाप्त हो जाता है।
• कुछ लोग गणित में अज्ञानी की तरह बात करते हैं जैसे किसी वास्तविक संख्या को शून्य से विभाजित करने पर हमें अनन्त संख्या प्राप्त होती है। अव्वल तो वास्तविक संख्या से विभाजित नहीं किया जा सकता और दूसरी बात अनन्त कोई संख्या नहीं है यह केवल हमारी सीमा को प्रकट करता है कि यह असम्भव है। कई मनुष्य सोचते हैं कि वे गणित में खुद के नियम और स्वयंसिद्ध बना सकते हैं उनका ऐसा सोचना गलत नहीं है क्योंकि हर मनुष्य को ऐसा सोचने और करने का अधिकार है। परन्तु अव्वल तो ऐसा न तो स्वयं के नियम व स्वयंसिद्ध बना सकते हैं। यदि बना भी ले तो उनको सुसंगत तरीके से सिद्ध करना मुश्किल है।
• गणित किसी अभिजात्य तथा ऊँचे पढ़े-लिखे, एलिट वर्ग के लिए ही नहीं है यह सार्वभौमिक है सबके लिए उपलब्ध हैं इसमें योगदान दे सकते हैं और उपयोग में ले सकते हैं।आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें ।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।

2.गणित:एक सुंदर बात बदसूरत बना दिया (Mathematics A Beautiful Thing Made Ugly),मैथमेटिक्स: ए ब्यूटीफुल थिंग मेड अग्ली(Mathematics: A Beautiful Thing Made Ugly):

• क्या सोशल मीडिया ने गणित की गलतफहमी और मिस-एप्लिकेशन को एक नए स्तर पर ले लिया है?

3.एक सुंदर वस्तु (A Beautiful Thing):

• मेरे पिता,जिनकी स्कूली शिक्षा काफी बुनियादी थी,मुझे गणित की सराहना देने के लिए काफी हद तक जिम्मेदार थे।दुर्घटना से कुछ हद तक, विश्व युद्ध दो ने उसे संख्या में गहरा कर दिया।युद्ध पूर्व इंग्लैंड में वह एक कॉस्मेटिक कंपनी के लिए एक मुनीम था।हिटलर ने आक्रमण की धमकी देते हुए सेना में शामिल होने का फैसला किया।उनके सपाट पैरों ने उन्हें लड़ाकू कर्तव्यों के लिए अनुपयुक्त बना दिया,इसलिए भर्ती करने वाले ने कहा कि वह एक मुनीम था, ने कहा,”आप संख्याओं के बारे में जानते हैं,आप इंजीनियरों से जुड़ सकते हैं”।इस प्रकार वह कोर ऑफ रॉयल इलेक्ट्रिकल और मैकेनिकल इंजीनियर्स में शामिल हो गया और बीजगणित,कलन,त्रिकोणमिति और सम्मिश्र संख्याओं का अध्ययन करने के लिए बनाया गया था,जो सभी उसे मोहित कर रहे थे।उन्होंने काम के क्रम में ब्रिटेन के युद्ध-काल के रडार को बनाए रखने में मदद करने के लिए जो सीखा था उसे लागू किया।संघर्ष के बाद वह ऑस्ट्रेलिया चले गए,जहां उन्होंने गणित का उपयोग किया,जिसमें झाड़ी के लिए प्रौद्योगिकी डिजाइन करना और आपूर्ति करना था जो कि अन्य रिटर्निंग सर्विसमैन द्वारा कृषि के लिए खोला जा रहा था।टेलीविज़न अंततः उनके व्यवसाय का मुख्य केंद्र बन गया,लेकिन इसके आने से पहले उन्होंने फायरट्रैक और 32V-240V DC-AC इनवर्टर के लिए दो तरफ़ा रेडियो बनाए क्योंकि ग्रामीण बिजली ग्रिड अभी भी अपनी प्रारंभिक अवस्था में था।

 

                                            (द ब्यूटीफुल: एम सी एस्चेर मोबीस स्ट्रिप)                                      

• मेरे पिता के लिए,खुद और कई अन्य लोगों के लिए, गणित केवल उपयोगी ही नहीं,बल्कि एक पेचीदा और सुंदर चीज भी है। हर दिन के साधारण अंकगणित से परे,झूठ के पैटर्न,सोच के नए तरीके और कई अद्भुत और कभी-कभी बेतुका परिणाम समस्याओं के लिए होता है।बेतुका अक्सर एक उपन्यास विचार में खुद को हल करता है जो अभी तक अनसुना कर देता है।हम में से कुछ धन्य थे कि हमारी आँखें इनमें से कुछ के लिए खुली थीं:
  मोबियस पट्टी,केवल एक तरफ के साथ कागज का एक टुकड़ा,
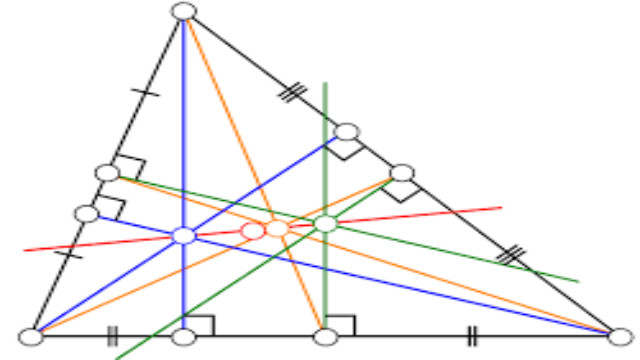
  काल्पनिक संख्याएँ,संख्याएँ जिनके पास कोई वास्तविक पदार्थ नहीं है लेकिन वास्तविक दुनिया में उपयोग के असंख्य हैं,
• त्रिभुज के साथ जुड़े लाइनों,अंक और हलकों के हजारों,
  अराजकता सिद्धांत और इसकी खूबसूरती से जंगली और रंगीन प्रतिनिधित्व,
  कुछ विचित्र और असामान्य संख्याओं के गुण जैसे 1089,सौहार्दपूर्ण संख्याएँ,मिलनसार संख्याएँ,हाइलस्टोन संख्याएँ,उत्तम संख्याएँ,पारलौकिक संख्याएँ और वास्तव में अजीब जैसे कि यूलर-मसोचोनी स्थिरांक।

• (यूलर की रेखा (लाल) सेंटीरोइड (नारंगी),ऑर्थोसेंटर (नीला),परिधि (हरा) और नौ-बिंदु सर्कल (लाल) के केंद्र के माध्यम से एक सीधी रेखा है।) 
• अफसोस की बात है,यह ऐसा प्रतीत होता है जो मैंने पिछले कुछ वर्षों में देखा है और अब मीडिया में और विशेष रूप से सोशल मीडिया में यह देखता हूं कि औपचारिक शिक्षा में लोगों ने गणित के बारे में जो सीखा है,वह काफी हद तक स्नातक स्तर पर पिघल जाता है।बहुतों ने गणित के चमत्कार नहीं देखे होंगे।वे परीक्षाओं को पास करने के लिए पर्याप्त जानते थे,लेकिन यह भी कि ज्ञान अल्पकालिक साबित हुआ।इसके अलावा, स्नातकों के रूप में,उन्होंने गलत विचारों को चुनना और उनके साथ चलना जारी रखा है।लक्षण संभावना और आंकड़ों के बारे में विचित्र विचारों के माध्यम से संख्याओं की नींव और भाषा के बारे में समझने की पूरी कमी से लेकर हैं।संख्याओं के बारे में किसी भी तरह की जिज्ञासा को खोने के लिए,गणितीय ज्ञान और समझ को बनाए रखने के लिए या इससे भी बदतर,एक स्थानापन्न विकल्प लेने के लिए,क्या, मेरा मानना ​​है,व्यक्तियों और पूरे समाज पर हानिकारक प्रभाव पड़ता है।सोशल मीडिया में,मैं न केवल इस गिरावट का निरीक्षण करता हूं,बल्कि मैं समाज के हर हिस्से में गणितीय अज्ञानता के लिए एक जालीदार नाली देखता हूं।
• खूबसूरती को भुला दिया जाता है।अच्छा अभ्यास छोड़ दिया जाता है।मन अब आंदोलित नहीं होता।हम खतरे में हैं।

• (बदसूरत: गणित के सटीक नियम अब नहीं हैं।)
• विषय के प्रश्नों पर विचार करने से पहले हम थोड़ा अलग प्रश्न पर विचार करें: औपचारिक शिक्षा के बाद गणित का क्या होता है? क्या डिग्री या डिप्लोमा हासिल करने का मतलब अचानक गणित के जमीनी नियम बदल जाना है? क्या इसकी भाषा कुछ कम सटीक है? (मुझे डर है कि यह शिक्षा प्रणाली के भीतर ही हो रहा है,लेकिन यह एक अन्य लेख का विषय है।) क्या स्नातक,अशुद्धता के साथ,अचानक या बर्दमास (उर्फ PEDMAS) नियम को खारिज कर सकते हैं और कोष्ठक और निर्देश के आदेश की अनदेखी कर सकते हैं? कई लोगों के लिए,यहां तक ​​कि बराबर चिह्न,”=”,सटीक समानता के बजाय अस्पष्ट निहितार्थ का प्रतीक बन गया लगता है।वे कभी-कभी मूर्खतापूर्ण बातें करना चाहते हैं जैसे कि वास्तविक संख्या को शून्य से विभाजित करना और उत्तर को ¹अनंतता ’कहना, और फिर इसे संख्या की तरह व्यवहार करना।कुछ… 0.333 की बराबरी करने वाली अवधारणाओं के साथ भ्रमित हो जाते हैं … (पुनरावर्ती दशमलव याद रखें? ‘…’ यहां का अर्थ है कि 3s हमेशा के लिए चलते हैं) और 0. = 0.666 … और जब आप उन्हें \frac{2}{3} \text{ को }\frac{2}{3} में जोड़ने के लिए कहते हैं और उन्हें 1 मिलता है, लेकिन 0.333 जोड़ते हैं। … 0.666 के लिए … वे आपको बताते हैं कि यह 0.999 है … और कोई तरीका नहीं है जो 1 के बराबर है। (ठीक है मुझे एक संख्या दें जो 0.999 के बीच मौजूद है … और 1. उम्म … अब इस समानता के लिए एक औपचारिक प्रमाण है,लेकिन इसके लिए नहीं इस बार या मंच।) यहां तक ​​कि मुझे भी नहीं मुझे pi( (π) =22/7  के बराबर होने की शुरुआत करने दें और “कानून के कानून” के बराबर होने दें।

4.गणित का आधार (The Basis of Mathematics):

• गणित तर्क का विस्तार है और यह स्वयंसिद्ध पर आधारित है।स्वयंसिद्ध सहमत हैं,अक्सर स्व-स्पष्ट,सत्य जो स्वयं सिद्ध नहीं हो सकते हैं।हम तर्क के नियमों (जो स्वयं स्वयंसिद्ध हैं) को लागू करते हैं,आगे की सच्चाइयों को प्राप्त करने के लिए गणित के मूल,सहमत सत्य।स्वयंसिद्धों की वैधता दर्शन का विषय है,तर्क का नहीं।जब तक हम दार्शनिक बहस में प्रवेश नहीं करना चाहते हैं,तब तक हमारे लिए सही और प्रभावी गणित का क्षेत्र निर्धारित किया गया है।गणित को उपयोगी बनाने और बनाए रखने के लिए,यदि मैं कहता हूं, सुंदर बनाने के लिए Axioms और उन्हें हेरफेर करने के लिए उपयोग किए जाने वाले नियम अपरिवर्तनीय हैं (हालांकि उन्हें नए क्षेत्रों में जोड़ा जा सकता है)।

5.भद्दापन (The Ugliness):

• विशेष रूप से इंटरनेट और सोशल मीडिया ने समस्या को बहुत बढ़ा दिया है।जबकि अच्छे और दिलचस्प गणित को बढ़ावा देने के लिए समर्पित साइटें हैं,माध्यम की प्रकृति “एक अच्छा पर्याप्त” रवैया है।विषय विषय से एक वाक्यांश उधार लेने के लिए “सबसे कम आम भाजक” मानक बन जाता है।अच्छे गणित साइट मंचों में टिप्पणियों को पढ़ें और यह जल्दी से स्पष्ट हो जाता है कि बहुत से ऐसे विचार हैं जो साइट साझा कर रहे हैं के सामने उड़ते हैं।एक बार इस तरह के प्रतिवादी ने एक मंच पर एक विचार रखा है,ऐसे अन्य लोग हैं जो स्पष्ट रूप से सीखना कोई इच्छा नहीं रखते हैं।वे केवल अज्ञान की आग में ईंधन जोड़ना चाहते हैं।
• मेट्रोपोलिस के श्रमिकों की तरह बहुत से लोग हैं जो अंधेरे (अज्ञानता) में अनजान हैं कि मानव मन के लिए दिन के उजाले (ज्ञान) में खिलाने के लिए और भी बहुत कुछ है।

6.अराजक तरीके (Anarchic Methods):

• आमतौर पर, ज्यादातर लोगों को स्नातक होने के बाद औपचारिक बीजगणित,कलन और त्रिकोणमिति पर लटकने का कोई औचित्य नहीं है। मेरा तर्क यह है कि अगर ऐसा है तो उन्हें इससे खिलवाड़ नहीं करना चाहिए।लेकिन अब गणितीय भूलने की बीमारी वाले लोगों के पास एक मंच है – इंटरनेट।यह गणितीय और तार्किक पहेलियों के साथ समाप्त हो जाता है जो खराब रूप से तैयार की जाती हैं और केवल समस्या को बढ़ाती हैं: जिस अनुक्रम के लिए आपको केवल एक सही उत्तर की अनुमति दी जाती है,विस्मयकारी एंटीकेडेंट्स,समान चिह्न का अवैध उपयोग,कोष्ठक के बिना थोड़ा जटिल अंकगणितीय समस्या।और इसलिए,चूंकि वे सही नियमों को भूल गए हैं और चूंकि किसी और ने समस्या को निर्धारित करने के लिए अपने स्वयं के नियम बनाए हैं,वे कहते हैं कि “मैं इसे हल करने के लिए अपना खुद का बनाऊंगा।”निश्चित रूप से,आप अपने स्वयं के स्वयंसिद्ध और नियमों का आविष्कार कर सकते हैं।कुछ गणितज्ञ हर समय करते हैं,लेकिन आपके नियमों और स्वयंसिद्धों के सुसंगत होने की संभावना नहीं है और जरूरी नहीं कि एक समस्या को सही ढंग से हल करें जिसे हम सामान्य,रोजमर्रा की दुनिया कह सकते हैं।यह अराजकता द्वारा समाधान है लेकिन एक और समान रूप से बुरा विचार है।

7.लोकतंत्र द्वारा समाधान (Solution by Democracy):

• सोशल मीडिया आम तौर पर इन समस्याओं को मनोरंजन के रूप में दुनिया के सामने पेश करता है।यह शिक्षाप्रद है क्योंकि “एम्यूज़” शब्द “ए” का अर्थ “बिना” और “म्यूज़” का अर्थ “विचार” से है।ये गणितीय tidbits अपने दर्शकों के एक हिस्से को मेमोरी लेन में एक समय के लिए यात्रा करने के लिए आमंत्रित करते हैं,जब, शायद,वे ऐसी चीजों को समझते थे।लेकिन,अफसोस कि यह जगह मातम के साथ बह गई,इसका रंग छलक रहा है और यह अंधेरे में डूबा हुआ है।यह उनके सामने समस्या के लिए बहुत कम रोशनी प्रदान करता है।जैसा कि सही उत्तर उनमें से कई को हटाता है,वे फिर से अपने स्वयं के नियमों का आविष्कार करते हैं,उन नियमों के अनुसार समस्या को हल करते हैं और अपनी पसंद का समाधान पोस्ट करते हैं।कई व्यक्ति इस तरह के समाधान पोस्ट करते हैं कि एक आम सहमति “सही” उत्तर का खुलासा करती है।इस तरह की सूचियों का मेरा पढ़ना यह है कि कई लोग,गलत ठिकानों का उपयोग करते हुए,किसी अन्य व्यक्ति की तरह एक समाधान ढूंढते हैं और इसे सूची में जोड़ते हैं, जैसा कि उन्हें सही मिला।बदले में,समाधानों को पढ़ते हुए,बस विभिन्न समाधानों और आंकड़ों की आवृत्ति पर देखें कि बहुमत का उत्तर सही होना चाहिए।
• समस्या का हिस्सा यह है कि सोशल मीडिया में गणित के लिए कोई अंपायर या मध्यस्थ नहीं है।ऑनलाइन गणितीय aficionados के एक समूह को छोड़कर,जो,मुझे लगता है,वास्तविक चीज़ के पक्ष में ऐसे अतीत-काल से बच जाएगा और वोल्फ्राम अल्फ़ा जैसी कई गणितीय उन्मुख वेबसाइटें,जो कुछ हद तक निष्क्रिय हैं,क्रम में मुड़ने के लिए कहीं नहीं है।गणितीय प्रसिद्धि के लिए किसी भी सामान्य व्यक्ति के दावे को सत्यापित करने के लिए।
  अराजकता या लोकतंत्र द्वारा गणितीय समस्या हल करने के वास्तविक परिणाम हैं।

8.परिणाम 1. एक उच्च बुद्धि और अन्य व्यक्तिगत घोंघे का झूठ (Consequence 1. The lie of a high IQ and other personal snares):

• सोशल मीडिया में अधिकांश पहेलियाँ खराब समझ दिखाने के लिए जाल हैं।वे बुद्धि को उत्तेजित नहीं करते हैं।वे मज़ेदार हो सकते हैं,लेकिन इसलिए वास्तविक और अच्छी तरह से समस्याओं को एक साथ रख सकते हैं।
  गणितीय क्षमता आवश्यक रूप से बुद्धि का मापक नहीं है।तार्किक रूप से सोचने की क्षमता हो सकती है।रचनात्मकता निश्चित रूप से है। सामाजिक बुद्धिमत्ता,सामाजिक रिश्तों और परिवेशों की पच्चीकारी के माध्यम से आगे बढ़ने और प्रबंधित करने की क्षमता,जीवन को हमारे ऊपर फेंकती है,निश्चित रूप से।सोशल मीडिया झूठ कहता है कि हम में से उस हिस्से को पैंडर है जो उज्ज्वल,मजाकिया,किसी के लिए पहचाना जाना चाहता है।यह अपने दर्शकों को स्वीकार किए जाने या दूसरों की तुलना में बेहतर बनाने के लिए तुच्छ और गलत समस्या हल करने वाले अभ्यासों को बढ़ावा देता है।यह गणितीय क्षमता को बढ़ाने,बढ़ाने या सही करने या बुद्धि बढ़ाने के लिए बहुत कम है।मूल रूप से,यह अज्ञानता को बढ़ावा देता है ।
• क्या गणित से बुद्धि में सुधार हो सकता है? गणित,गणित,पद्य,IQ के लिए बहुत कम करेगा,लेकिन इसके द्वारा उपयोग की जाने वाली प्रक्रियाएं, रचनात्मकता इसे संलग्न करती है और इसे भड़काने वाली चुनौतियां।जैसा कि एंड्रिया कुस्ज़वेस्की बताते हैं:
• इंटेलिजेंस केवल इस बात के बारे में नहीं है कि आपने कितने स्तर के गणित पाठ्यक्रम लिए हैं,आप कितनी तेजी से एक एल्गोरिथ्म को हल कर सकते हैं या आप कितने शब्दावली शब्दों को जानते हैं जो 6 वर्णों से अधिक हैं।यह एक नई समस्या का सामना करने में सक्षम होने,इसके महत्वपूर्ण घटकों को पहचानने और इसे हल करने में सक्षम है-फिर उस ज्ञान को प्राप्त करें और इसे अगली,अधिक जटिल समस्या को हल करने की दिशा में रखें।यह नवाचार और कल्पना के बारे में है और दुनिया को एक बेहतर जगह बनाने के लिए उपयोग करने में सक्षम होने के बारे में है।यह उस प्रकार की बुद्धिमत्ता है जो मूल्यवान है और यह उस प्रकार की बुद्धिमत्ता है जिसके लिए हमें प्रयास करना चाहिए और प्रोत्साहित करना चाहिए। (एंड्रिया कुज़ेव्स्की, 7 मार्च, 2011)
• गणितीय सिद्धांतों की खराब समझ रखने से भी इसे लिया जा सकता है।यहाँ पर गणित और सामाजिक बुद्धिमत्ता का मेल होता है।यह सौदेबाजी हो सकती है जो कोई सौदा नहीं है।उदाहरण के लिए,यह एक पिरामिड से समृद्ध योजना (पॉन्ज़ी) हो सकती है।यह केवल इस बात पर विचार हो सकता है कि उनके लॉटरी जीतने के पूर्वानुमान के तरीके हैं।
  इसके अलावा,यदि आप इसे इंटरनेट पर गलत पाते हैं,तो आपने अपनी पहचान (संभवतः आपके सबसे बेशकीमती सामाजिक कब्जे) को दागदार कर दिया है,जो पूर्ववत करना बहुत मुश्किल हो सकता है।इस समस्या पर विचार करें,जो लिंक्डइन पर अपने कई अवतारों में से एक में दिखाई देने पर,निम्नलिखित प्रतिक्रियाओं को उकसाया।

• एक व्यावसायिक सलाहकार से:”कोष्ठक के बिना एक समीकरण के लिए, बिना किसी विरोधाभासी निर्देशों के बिना बाएं से दाएं आगे बढ़ना, फिर 6 -1 = 5 x 0 = 0 + 2 = 2/2 = 1″।मुझे यकीन नहीं है कि मैं उसके साथ किसी भी चीज के बारे में परामर्श करूंगा,जिसमें पैसे भी शामिल हों।
• एक कंप्यूटर सिस्टम वास्तुकार,हालांकि उसे सही उत्तर मिला,एक सार्वजनिक मंच में,गणित को कैसे पढ़ाया जाता है,इस बारे में उसकी समझ में रास्ता: “यह अलग-अलग उत्तरों के साथ एक और है जहां आपको गणित और संचालन का क्रम सिखाया गया था ( आप कैलकुलेटर के बिना गणित कर सकते हैं या नहीं)। मेरे मामले में यह BODMAS है जहाँ गुणन और विभाजन को जोड़ और घटाव से पहले हल किया जाता है, इसलिए इसका उत्तर है 7. यह _not_ है जिसे अलग-थलग करने के लिए छोड़ दिया गया संचालन के अनुक्रम के रूप में किया जाता है। “मैं गलत हो सकता हूं, लेकिन मेरा मानना ​​है कि गणित।दुनिया-भर में इसी तरह सिखाया जाता है।इसे हल करने का केवल एक ही तरीका है।

9.नतीजा 2. हम सबके लिए डरावना सामान (Consequence 2. Scary stuff for us all):

• हम अपने जोखिम पर गणित की सटीकता के साथ खेलते हैं।यदि हम मान लें कि हम इस क्षेत्र में वास्तविक और परीक्षण किए गए कौशल के बिना कुछ जानते हैं तो हम अपने लिए,दूसरों के लिए और संभवतः दुनिया के लिए खतरे पैदा करते हैं।कुछ तिमाहियों में,विशेष रूप से सोशल मीडिया में, कि गणित किसी भी तरह एक सहज कौशल है,बुद्धि का एक उपाय है,कुछ लोगों को आगे बढ़ाता है-ऐसे लोग जो हमारे कल्याण पर नियंत्रण रखते हैं – यह सोचने के लिए कि वे उस गणित से या उसके बारे में निर्णय कर सकते हैं जो इसे नियंत्रित करता है कल्याण।

10.इंटरनेट सुरक्षा के लिए खतरा (Threats to Internet safety):

• हमने हाल ही में कानून प्रवर्तन अधिकारियों,राजनेताओं और यहां तक ​​कि मशहूर हस्तियों का एक समूह देखा है,जो एन्क्रिप्शन एल्गोरिदम में बैक-डोर होने के तर्क पर वजन कर रहे हैं जो इंटरनेट और अन्य जगहों पर हमारे डेटा की रक्षा करते हैं।
• सटीक और सुरुचिपूर्ण गणित आपकी व्यक्तिगत जानकारी की सुरक्षा करता है।क्या आप इस ग्राफ़िक में त्रुटि चुन सकते हैं?
• यह स्पष्ट है कि अधिकांश यह सुनिश्चित करने के लिए पर्याप्त गणित भूल गए हैं कि वे डेटा को एन्क्रिप्ट करने वाले अंतर्निहित एल्गोरिदम को अब समझ नहीं सकते हैं।इस तरह के एन्क्रिप्शन पर आधारित है और ध्वनि गणित द्वारा परीक्षण किया गया है।अपराधियों और आतंकवादियों को पकड़ने में मदद करने के लिए एन्क्रिप्शन को कमजोर करने का विचार सराहनीय हो सकता है लेकिन किस कीमत पर? क्रिप्टोग्राफी के सटीक गणित के साथ खिलाने से इसकी उपयोगिता कम हो जाती है।कानून प्रवर्तन के लिए एल्गोरिदम को कमजोर करने का मतलब है कि उन्हें किसी और हर किसी के लिए कमजोर करना।एन्क्रिप्शन में उपयोगिता की हानि का अर्थ है कि हम सभी अपनी दुनिया में दुर्भावनापूर्ण पात्रों और कारणों से हार जाते हैं।(आधुनिक समय के संचार में प्रदान की गई गोपनीयता के इस साधन को ध्वस्त नहीं करने के अच्छे, गैर-गणितीय कारण भी हैं)।

• गणित की एक बुनियादी समझ खोना और इसे कुछ टीडीपीड विकल्प के साथ बदलना,सोशल मीडिया के मानकों द्वारा समर्थित,किसी को भी क्रिप्टोग्राफी जैसे क्षेत्रों के बारे में मान्य राय तैयार करने से अयोग्य घोषित करता है।दो शताब्दियों से अधिक की अवधि में आज के एन्क्रिप्शन तरीकों को जन्म देने वाले दिमाग गणित में फंस गए थे।अगर मार्टिन हेलमैन,व्हिटफील्ड डिफी,नील कोब्लिट्ज,विक्टर मिलर,रॉन रिवरेस्ट आदि शमीर,लियोनार्ड एडलमैन,यूक्लिड, सन त्ज़ु, लियोनहार्ड यूलर,अल्वारीस्टिन गालोइस और एलन ट्यूरिंग के नाम का कोई सार्वजनिक आंकड़ा नहीं है, तो मैं (सम्मानपूर्वक) उन्हें सुझाव देता हूं।एन्क्रिप्शन के बारे में घोषणा करने से पहले गणित में उनके योगदान का अध्ययन करें।

11.न्याय के गर्भपात (Miscarriages of Justice):

• गणित, विशेष रूप से आंकड़े,आधुनिक अदालती कार्यवाही में एक महत्वपूर्ण प्रमाणिक भूमिका निभाते हैं।गणितीय ज्ञान के आधार पर अपराध या निर्दोषता का आकलन करने के लिए वकीलों,न्यायाधीशों और जजों को अपनी सीमाएं जानने की आवश्यकता होती है।गणित के प्रकाश में साक्ष्य की व्याख्या करते समय कई महान और निष्पक्ष कानूनी दिमाग पहले से ही पीछे की ओर होंगे,आखिरकार,वरिष्ठ शिक्षा में गणित के बारे में सबसे अधिक चुना गया कानून।गणितीय झूठ और तुच्छता के दायरे को जोड़ें,जो सोशल मीडिया में व्याप्त है और हम केवल एक नकारात्मक प्रवृत्ति देख सकते हैं-’फन’ के गणित पर लागू अराजकता और लोकतंत्र अन्यथा झूठ और तुच्छता में तथ्यात्मक साक्ष्य को बदल देगा।
• मैं निम्नलिखित तीन मामलों का हवाला देता हूं,इसलिए नहीं कि उनके पास महान सोशल मीडिया कवरेज था,बल्कि इसलिए कि वे दिखाते हैं कि ऐसी प्रणाली में क्या हो सकता है जहां गणित का व्यवहार बिना कठोरता के किया जाता है और कभी-कभी तिरस्कार के साथ।सोशल मीडिया एक ऐसी प्रणाली है।
• वास्तविकता का प्रतिनिधित्व करने का सांख्यिकी का अपना तरीका है। (Commons.wikimedia.org)
  2001 में हेग के एक अस्पताल में उसकी देखभाल में 6 महीने के बच्चे की स्पष्ट विषाक्तता के बाद एक नर्स लूसिया डी बर्क को 2001 में गिरफ्तार किया गया था।डे बर्क की शुरुआती गिरफ्तारी के बाद,उसकी देखभाल के तहत संदिग्ध मौतों और रोगियों की निकट मृत्यु के पैटर्न के बारे में सोचा गया था,इसे उजागर किया गया था।सांख्यिकी ने जांच और उसके बाद के परीक्षणों में एक महत्वपूर्ण भूमिका निभाई।एक अदालत ने सांख्यिकीविद नियुक्त किया,जो कुछ शौकिया था,उसने गणना की कि यह 342 मिलियन अवसरों में से एक होगा,यह शुद्ध संयोग था कि वह ड्यूटी पर था जब सभी घटनाएं हुई थीं।दो परीक्षणों के बाद उसे नौ हत्याओं का दोषी पाया गया और 3 में हत्या का प्रयास किया और बिना किसी पैरोल के साथ आजीवन की सजा सुनाई।गणितीय ज्ञान की कमी के कारण,इन मामलों में न्यायाधीश क्या नहीं देख सकते थे, यह था कि सांख्यिकीय प्रक्रियाओं का उपयोग त्रुटिपूर्ण था।2004 में आजीवन के लिए जेल में डाल दिया गया था आखिरकार उसे 2008 में अपील की अनुमति देने के लिए छोड़ दिया गया था और 2010 में उसे राज्य का मुआवजा दिया गया था।किसी के जीवन के नौ साल जो आसानी से खराब गणित ने ले लिए हैं? हाँ,ऐसा लगता है।
• 3 अक्टूबर 2011 को,ब्रिटिश एक्सचेंज के छात्र मेरेडिथ केचर की हत्या के दोषी अमांडा नोक्स और रैफेल सोलेसीटो को एक इतालवी अदालत में बरी कर दिया गया था।एक पूर्व अपील न्यायाधीश ने घटनास्थल पर एक चाकू पर पाए गए माइनसक्यूल डीएनए नमूने का पुन: परीक्षण करने का फैसला किया था,जिसमें कहा गया था,”दो परिणामों का योग,दोनों अविश्वसनीय … एक विश्वसनीय परिणाम नहीं दे सकते।”वह गलत था। जबकि सहज ज्ञान युक्त,यह गणितीय रूप से सटीक नहीं है।अपेक्षाकृत अविश्वसनीय परीक्षणों को दोहराना उन्हें अधिक सांख्यिकीय रूप से विश्वसनीय बना सकता है।जब सेवानिवृत्त मुलज़िम चला गया और अभियुक्त के पक्ष में पाया गया,तब रिट्रीटिंग हुई,लेकिन कुछ समय बाद तक सुप्रीम कोर्ट ऑफ कसेशन (इटली की सर्वोच्च अदालत) ने यह फैसला सुनाया कि नॉक्स और सोललेसीटो हत्या में शामिल थे।यदि मूल अपील न्यायाधीश के पास थोड़ा सा सांख्यिकीय ज्ञान होता,तो पहले के लिए कई परीक्षणों को बुलाया जा सकता था और आरोपी के दर्द को बख्शा जाता था।
• एक और मामला सैली क्लार्क का है।उसे 1999 में अपने दो बेटों की हत्या के मामले में ब्रिटेन में दोषी ठहराया गया था।क्लार्क के दोनों बच्चे खाट-मौत (एसआईडीएस) से मर चुके थे और उनकी हत्या के लिए गिरफ्तार होने के लंबे समय बाद भी नहीं।उसके खिलाफ मामला एक प्रतीत होता है निर्विवाद सांख्यिकीय पर आधारित था।एक प्रतिष्ठित बाल रोग विशेषज्ञ ने गवाही दी कि एक ही परिवार के दो बच्चों की खाट-मौत से मौत का मौका 73 मिलियन में से एक था।अपील की अनुमति मिलने तक उसे चार साल की सजा हुई और जेल में बंद कर दिया गया।मुख्य गवाह,अन्य बातों के अलावा,इस बात पर ध्यान देने में विफल रहा कि दोनों मौतें स्वतंत्र नहीं थीं।उन्होंने इस तरह की दो मौतों के स्वतंत्र अवसरों को कई गुना बढ़ा दिया था।यदि उन्होंने पर्याप्त गणित को बरकरार रखा होता, या एक निष्पक्ष सांख्यिकीविद् को उनकी गवाही का खंडन करने के लिए बुलाया जाता था,तो यह संदिग्ध है कि सैली क्लार्क ने उन वर्षों को जेल में बिताया होगा।
• इन मामलों में,और शायद कई अन्य जिन पर कभी भी सवाल नहीं उठाया जाएगा,शो यह है कि अपराध या निर्दोषता का निर्धारण करने में इसका सही उपयोग करने में सक्षम होने के लिए गणित का एक सही ज्ञान आवश्यक है।गणित के लिए सोशल मीडिया का दृष्टिकोण निर्देश की ओर जाता है,न कि समझने का,बल्कि अज्ञानता और तुच्छीकरण का।यह गणित के एक खराब उपयोग को बढ़ाता है जहां यह महत्वपूर्ण है।न्यायाधीशों को अपनी सीमाएं पता होनी चाहिए, और संभवत: जूरी के ज्ञान की सीमाएं, और, मैं न्याय की खोज में गणितीय विशेषज्ञों को नियुक्त करता हूं।
  अज्ञान = चतुरता पूर्ववत्

• या इसका विलोम (?) चतुरता=अज्ञानता का किया हुआ अंत! छद्म गणित का इस्तेमाल अक्सर किसी को चतुर दिखने के लिए किया जाता है। कभी-कभी यह बुरी तरह से विफल हो जाता है।विपरीत ग्राफिक को देखो।फिर से यह लिंक्डइन से था।यह उपमा का एक घटिया विकल्प था। मुझे लगता है कि क्या इरादा था.r ∝ nᵐ। लेखक ने फ़ंक्शन को परिभाषित नहीं किया।जिस बिंदु को वह बनाने की कोशिश कर रहा था वह इसके बिना हो सकता था।यह सब फंक्शन एफ की प्रकृति पर निर्भर करता है।यदि आप समझते हैं कि हम f (x) = 0 को परिभाषित कर सकते हैं,तो कोई भी बात नहीं है कि n और m,r हमेशा शून्य होंगे – कोई प्रतिरोध नहीं! मैं उचित समझ के बिना गणितीय उपमाओं का उपयोग नहीं करने का सुझाव दूंगा क्योंकि यह दर्शकों को प्रभावित कर सकती है।
  बुरा … इर्र … नहीं! – STUPID निरूपण
                        o%  Fail Answer

• सोशल मीडिया में देखे जाने वाले ट्रैप्स में आकर्षक रूप से गणितज्ञों को उन समस्याओं को हल करना शामिल है जो खराब रूप से तैयार की जाती हैं।कुछ,एक विपरीत की तरह,वहाँ तर्कों को उकसाने के लिए रखा जाना लगता है।मेरा सुझाव है कि इस तरह की समस्या को प्रस्तुत करना केवल गणित के बारे में बुरे विचारों के लाभ को जोड़ता है।यह सोचने वाले दिमाग के लिए कुछ नहीं करता है।
• समस्या को हल करने की क्षमता,बड़ी हद तक,सिखाया जा सकता है।
  शानदार जानकारी।
• कितने लोग यह पहचानेंगे कि इस पहेली की पहली पंक्ति बहुत ही शानदार डेटा है।उत्तर दूसरे दो का अंतर है।इस तरह की सोच दुनिया भर के ज्यादातर हाई स्कूलों में पढ़ाई जाती है।यह स्नातक होने के बाद खो जाता है।

12.निष्कर्ष के तौर पर (In Conclusion):

• गणित एक अभिजात वर्ग के लिए नहीं है।लेकिन यह प्रशिक्षित दिमागों के लिए है।अगर हम सही आधार पर निर्माण करते हैं तो इसकी सार्वभौमिक सत्यता,अगर सही ढंग से समझी जाए,तो हमारी बुद्धिमत्ता का मनोरंजन,शिक्षा और संवर्धन कर सकती है।सभी को लाभ।
• यदि हम सोशल मीडिया के माध्यम से,सामान्य लोगों को गणितीय आड़ में खिलाने के लिए आड़ में यह कहते हैं कि यह उनकी बुद्धि को खिलाएगा और उन्हें शिक्षित करेगा कि हम वास्तविक दुनिया की समस्याओं को समझें।उन समस्याओं को हल करने के लिए गणित का प्रभावी उपयोग न केवल कम है, बल्कि इसकी सुंदरता को कभी नहीं देखना

13.फुटनोट (Footnotes):

•                   2(1+2)=?
           9   or   1
  :BODMAS का खराब उपयोग
• गणितीय प्रणालियाँ हैं,उदाहरण के लिए, वास्तविक संख्याएँ,जहाँ अनंत को एक संख्या के रूप में माना जा सकता है,लेकिन वास्तविक संख्याओं के रूप में नहीं।
• गणितीय प्रणालियों में अक्सर विरोधाभास होता है।ये हमें यह सोचने के लिए प्रेरित कर सकते हैं कि प्रणाली में एक विसंगति है।हालांकि,क्या वे केवल व्यवस्था का हिस्सा नहीं बन सकते हैं या यहां तक ​​कि कुछ भी,जो समय के साथ कुछ उच्चतर सत्य में हल हो जाएंगे।इनमें से रसेल का विरोधाभास और हिल्बर्ट-बर्नसे_परडॉक्स प्रसिद्ध है
  कई अच्छी तरह से गणित की वेबसाइटों के साथ-साथ Youtube,Vimeo आदि में वीडियो डाले जाते हैं,लेकिन इस सामग्री से संबंधित टिप्पणियों को पढ़ने से मुझे अक्सर इस धारणा के साथ छोड़ दिया जाता है कि लोग इन साइटों को अज्ञानी के रूप में छोड़ देते हैं जैसे वे आए थे।
  बेशक, लॉटरी जीतने का एक तरीका है – बस सभी टिकट खरीदें।हालांकि, यह वित्तीय रूप से नासमझ है।
• उपर्युक्त आर्टिकल में गणित:एक सुंदर बात बदसूरत बना दिया (Mathematics A Beautiful Thing Made Ugly) तथा मैथमेटिक्स: ए ब्यूटीफुल थिंग मेड अग्ली(Mathematics A Beautiful Thing Made Ugly) के बारे में बताया गया है.

Mathematics A Beautiful Thing Made Ugly

गणित:एक सुंदर बात बदसूरत बना दिया
(Mathematics A Beautiful Thing Made Ugly)

Mathematics A Beautiful Thing Made Ugly

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Instagram	click here
4.	Linkedin	click here
5.	Facebook Page	click here