Mathematical problem solving in hindi
Contents
hide
1
गणितीय समस्या को हल करना का परिचय (Introduction to Mathematical problem solving),गणित में समस्या को हल करने के साथ समस्या (The Problem with Problem Solving in Mathematics):
गणितीय समस्या को हल करना का परिचय (Introduction to Mathematical problem solving),गणित में समस्या को हल करने के साथ समस्या (The Problem with Problem Solving in Mathematics):
- गणितीय समस्या को हल करना (Mathematical problem solving) के के द्वारा इस आर्टिकल में बताया गया है कि जब हम गणित में कोई समस्या हल करते हैं तो उसके साथ भी समस्या है। दरअसल समस्याएँ हमारे जीवन का हिस्सा है। हम समस्याओं को हल करते जाएं और आगे बढ़ते जाएं। समस्याओं का कोई अन्त नहीं होनेवाला है।
- आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:Problem solving
(1,)गणितीय समस्या को हल करना (Mathematical problem solving),गणित में समस्या को हल करने के साथ समस्या (The Problem with Problem Solving in Mathematics):):
Also Read This Article:Mathematician to be honored at csu pueblo president Gala
(2.)समस्या को हल करने, विचार है कि छात्रों को इन कौशल एक संदर्भ सीखने और उन्हें;एक और में लागू कर सकते है अनिवार्य रूप से गलत है(problem solving, the idea that students can learn these skills one context and apply them in another is essentially wrong):
- के रूप में Wiliam (२०१८) कहते हैं, ‘ के लिए.. । समस्या को हल करने, विचार है कि छात्रों को इन कौशल एक संदर्भ सीखने और उन्हें एक और में लागू कर सकते है अनिवार्य रूप से गलत है ।
- समस्या हल करने के लिए हमारी क्षमता एक विषय के बारे में बहुत कुछ जानने से आता है और समस्याओं को हल करने के लिए उस ज्ञान में हेरफेर करने में सक्षम किया जा रहा है । इसका मतलब है कि किसी भी समस्या को हल हम पूरा करना चाहते हैं, जैविक माध्यमिक ज्ञान और एक अच्छी तरह से जुड़े स्कीमा का एक मजबूत आधार से आना चाहिए, जबकि हमारी जन्मजात समस्याओं को हल करने की क्षमता बाकी का ख्याल रखना होगा, क्या संज्ञानात्मक वैज्ञानिकों को बुलाओ समस्या हल खोज,
- उस डोमेन के हमारे स्कीमा ड्राइंग और इसी तरह की समस्याओं है कि हम पहले से ही हल कर दिया है पहचानने । इस संबंध में, विषय डोमेन के भीतर समस्याओं को सुलझाने के प्राथमिक और माध्यमिक दोनों जैविक ज्ञान का एक अधिनियम है । शिक्षकों के रूप में हम सिर्फ ‘ अब ‘ में हमारे छात्रों के लिए उन में से एक पर नियंत्रण है । संज्ञानात्मक मनोवैज्ञानिक यह साल के लिए जाना जाता है और इस जानकारी के अंत में शिक्षकों के लिए नीचे धोखा दिया गया है । 21वीं सदी के इन कौशल को एकांत में नहीं सीखा जा सकता । वे एक विषय के विशाल ज्ञान पर निर्भर करते हैं ।
Also Read This Article:Learning progression for geometric transformation in mathematics
(3.)आँकड़ें वैज्ञानिक रूप से चुनौतीपूर्ण नहीं है के लिए नेतृत्व: सोच अच्छी तरह से तथ्यों को जानने की आवश्यकता है (Data is not scientifically challengeable: thinking well requires knowing facts):
- यहां क्या संज्ञानात्मक मनोवैज्ञानिक डैनियल Willingham (२०१०) को कहना है, ‘ पिछले तीस साल से डेटा एक निष्कर्ष है कि वैज्ञानिक रूप से चुनौतीपूर्ण नहीं है के लिए नेतृत्व: सोच अच्छी तरह से तथ्यों को जानने की आवश्यकता है, और यह सच नहीं है सिर्फ इसलिए कि तुम कुछ की जरूरत के बारे में सोचो । इस तरह के तर्क और समस्या को सुलझाने के रूप में सबसे अधिक महत्वपूर्ण सोच प्रक्रियाओं के बारे में शिक्षकों की परवाह है कि बहुत परिचित तथ्यात्मक ज्ञान के साथ intertwined रहे हैं कि दीर्घकालिक स्मृति में संग्रहीत किया जाता है (न सिर्फ पर्यावरण में पाया).
- संश्लेषण के लिए, आप केवल समस्याओं को हल कर सकते हैं जब आप तथ्यों को वास्तव में अच्छी तरह से जानते हैं, तो अच्छी तरह से, वे दीर्घकालिक स्मृति में स्थानांतरित कर दिया है ताकि आप एक समस्या को हल करने के लिए अपने काम स्मृति में उन तथ्यों में हेरफेर कर सकते हैं । और अगर आप समस्या एक क्षेत्र में हल कर सकते हैं, तो आप स्वचालित रूप से समस्या दूसरे में हल नहीं कर सकता ।
(4.)गणित छात्रों के साथ अभ्यास करने के लिए कुछ ज्ञान सिखाता है (Math teaches students some knowledge to practice with):
- मैं यहां थोड़ा मोड़ ले क्या एक प्राथमिक गणित सबक की तरह लग सकता है के रूप में करना चाहते हैं:
- श्री Barton राहेल Webster के साथ गणित podcast प्रकरण में: कैसे साल 7 है गणित सिखाया गया है, वह हमें एक संरचना है कि वह का उपयोग करता है कि मुझे लगता है कि कई प्राथमिक स्कूलों से परिचित है के माध्यम से लेता है । वह कुछ ज्ञान सिखाता है, छात्रों के साथ अभ्यास करने के लिए कुछ ‘ प्रवाह ‘ प्रकार के सवाल तैयार करता है और फिर तर्क और समस्या का एक बैंक है कि प्रवाह कौशल के आधार पर गतिविधियों को सुलझाने-यह निश्चित रूप से एक संरचना है कि मैं अपने शिक्षण से परिचित हूं । तो जब मैं कुछ मैं यहां सामान्यकरण पर हूं , वहां हम में से कुछ वहां से बाहर भी ऐसा ही होगा । यह ‘ त्वरित प्रगति ‘ के विचार से आया है । छात्रों को जल्दी से आगे ले जाएं, यदि उन्हें प्रवाह में 8 प्रश्न सही मिलते हैं, तो वे तर्क और समस्या समाधान के लिए तैयार हैं । यह मेरे लिए भावना बना दिया । जब तक मैं प्रदर्शन के बारे में सुना बनाम (Soderstrom, एन सी और Bjork, आर ए (२०१५))-तथ्य यह है कि इस विश्वविद्यालय में शिक्षण में आधारित मार्गों पर नहीं सिखाया जाता है, मेरी राय में, एक घोटाले के कुछ हद तक । आधार सरल है, क्योंकि छात्रों को अच्छा प्रदर्शन कर रहे हैं, इसका मतलब यह नहीं है कि वे इसे सीख रहे हैं, छात्रों को अच्छी तरह से प्रदर्शन के रूप में वे अपने काम में प्रक्रिया-स्मृति रखने में सक्षम है (या इसे पढ़ने के एक सफलता के मापदंड) और फिर तुरंत पर चले गए हैं ।
- जैसा कि हम जानते हैं, पता समस्याओं को हल करने के लिए इस जानकारी की आवश्यकता है हमारे दीर्घकालिक स्मृति में होने के लिए यह हमारे काम स्मृति है, जो, जब ज्ञान लागू करने का प्रयास केवल किसी एक समय में चार बातें पकड़ कर सकते है द्वारा हेरफेर करने के लिए । मुझे लगता है कि सफलता है कि छात्रों में से कुछ अनुभव हो सकता है जब जल्दी से दो बातों के लिए नीचे चला गया है । वे पहले से ही प्रवाह को जानता था और/या वे महसूस किया है कि समस्याओं को हम उन्हें दे प्रवाह के रूप में एक ही विषय पर वे पहले से ही प्रयास किया है । मदद करने के लिए छात्रों को बेहतर समस्या solvers हो, हम इस मॉडल से दूर ले जाने की जरूरत है और यह सुनिश्चित करें कि सभी आवश्यक प्रक्रियाओं और तथ्यों (जैविक माध्यमिक ज्ञान) अच्छी तरह से कर रहे है और वास्तव में उच्च पुनर्प्राप्ति शक्ति के साथ दीर्घकालिक स्मृति में एंबेडेड । सबसे अच्छा तरीका यह करने के लिए जानबूझकर अभ्यास, अधिक सीखने और महत्वपूर्ण तथ्यों और प्रक्रियाओं और भाषा की निरंतर स्थान पर समीक्षा के माध्यम से है ।
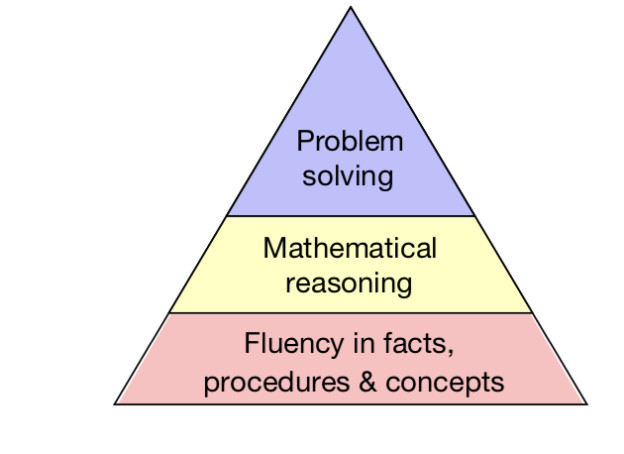
(5.)समस्या समाधान ,गणितीय तर्क तथा तथ्यों में प्रवाह ,प्रक्रिया और संकल्पना में सम्बन्ध (Relation between problem solving ,Mathematical reasoning and fluency in facts ,procedures & concepts):
- , Loughborough विश्वविद्यालय में गणित शिक्षा केंद्र में गणित शिक्षा में एक रीडर कॉलिन फोस्टर (२०१९) कहते हैं, ‘ मैं प्रवाह और गणितीय तर्क के बारे में सोचो, नहीं के रूप में अपने आप में समाप्त होता है, लेकिन के रूप में सभी का सबसे महत्वपूर्ण लक्ष्य में छात्रों का समर्थन करने का मतलब : समस्याओं को सुलझाना । उस कागज में वह इस पिरामिड का उत्पादन:
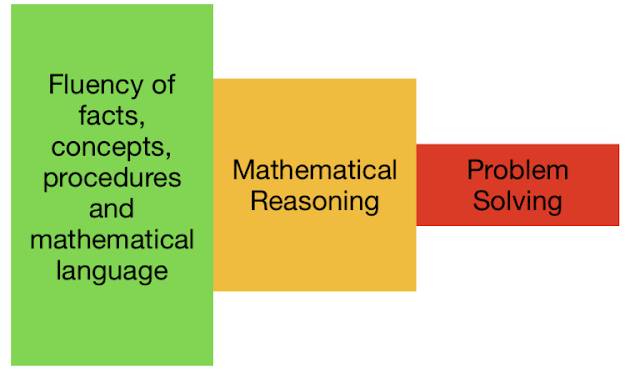
- लेकिन जैसा कि हम खिल के वर्गीकरण से जाना जाता है, जब पिरामिड और शिक्षा के मिश्रण, वे अक्सर गलत व्याख्या कर रहे हैं । इसके बजाय, मैं Clare है Sealy ब्लॉग से एक नोट ले और एक शंकु आकार के लिए जाना होगा ।
- फोस्टर से अनुकूलित (२०१९)
- इससे हमें यह देखने और समझने में मदद मिलती है कि शंकु के माध्यम से प्रगति करने के लिए, हमें मजबूत, डोमेन-विशिष्ट ज्ञान की आवश्यकता है, इस के साथ कारण करने में सक्षम हो और फिर गणितीय समस्याओं को हल करने के लिए सभी को एक साथ संयोजित करें । इसलिए यह समझना महत्वपूर्ण है कि तर्क और समस्या समाधान पहले एक साथ नहीं जाते हैं । वे अलग करने की जरूरत है और तर्क पहले सच समस्या को हल जगह ले जा सकते है पहले में महारत हासिल किया जाना चाहिए । सभी अनुसंधान मैं अभी तक उल्लेख किया है से निष्कर्ष स्पष्ट है-क्या आप एक छात्र समस्या को सुलझाने की क्षमता बस अभ्यास समाधान के द्वारा सुधार नहीं है ।
के रूप में Didau (२०१९) कहते हैं, ‘ जब novices के लिए एक समस्या है जिसके लिए वे एक सुविधा संग्रहीत समाधान नहीं है चेहरा, वे महंगा मतलब है अंत विश्लेषण पर निर्भर है । यह संज्ञानात्मक अधिभार के लिए नेतृत्व की संभावना है क्योंकि यह के माध्यम से काम करने की कोशिश कर रहा शामिल है और कई संभव समाधान मन में पकड़ । यह पिछले अभ्यास के बिना एक बार में पांच वस्तुओं हथकंडा की कोशिश की तरह एक सा है । समस्याओं को हल करने के लिए एक अकुशल तरीका समस्या को हल करने में बेहतर है । - जब आप अन्य उदाहरणों पर विचार करें, यह निस्संदेह समझ में आता है । तुम मैराथन के बहुत से चल रहा द्वारा मैराथन दौड़ में बेहतर नहीं मिलता है, तुम सिर्फ फुटबॉल के बहुत से खेलने के द्वारा फुटबॉल में बेहतर नहीं मिलता है और आप बार फिर से एक ही गीत खेलने के द्वारा संगीत रचनाओं का प्रदर्शन नहीं करते । आप पूरे के घटक भागों खोजने की जरूरत है, उन्हें अलगाव में अभ्यास और आप अपने अंतिम परिणाम प्राप्त जब तक उन्हें एक साथ रखा. जब एक मैराथन के लिए अभ्यास, आप कोर मांसपेशी विकास पर काम करने के लिए मदद से आप तेजी से चलाने के लिए, न सिर्फ कार्डियो कर सकते हैं; एक फुटबॉलर एक खेल के अलगाव में ड्रिब्लिंग अभ्यास अभ्यास और एक संगीतकार उनके trills अभ्यास एक जटिल संरचना का प्रयास करने से पहले अपनी उंगली गति और सहनशक्ति में वृद्धि हो सकती है । गणितीय समस्याओं को सफलतापूर्वक हल करने के लिए, हम deconstruct करने के लिए क्या यह समस्या ‘ हल ‘ उन्हें अलग है, और उंहें सिखाने की जरूरत है ।
- मुझे विश्वास है कि हम तर्क और समस्या एक ही है जहां वे अलग किया जाना चाहिए और गणितीय शब्दावली व्यवस्थित स्कूलों के माध्यम से नहीं पढ़ाया जाता है के रूप में हल देखते हैं । के रूप में ऊपर उल्लिखित, एक तरह से मुझे विश्वास है कि हम यह गलत है, प्रवाह से तर्क और समस्या को सुलझाने तक भी जल्दी से छात्रों को स्थानांतरित है । यह सब ज्ञान का निर्माण और यह दीर्घकालिक स्मृति में डाल समय लगता है ।
- चिंताजनक ढंग से और समान रूप से, यह अनुमान है कि यह दो साल लग सकते हैं, ‘ गणित एक छात्र के अनुकरणशील अभ्यास में उपयोग कर सकते है और कि वे पर्याप्त रूप से अवशोषित कर ली है और गैर में autonomously उपयोग के लिए दिनचर्या समस्या को सुलझाने के बीच । (बर्कहार्ट, २०१७) । यह शिक्षा में कई गणितज्ञों द्वारा समर्थित है । मैं इसे फिर से कहूंगा । यह एक व्यक्ति को वास्तव में नए गणितीय ज्ञान के साथ पर्याप्त धाराप्रवाह करने के लिए गैर नियमित समस्याओं को हल करने में सक्षम होने के लिए दो साल तक ले जा सकते हैं । देख के रूप में हम प्राथमिक छात्रों के साथ काम कर रहे हैं, मैं तर्क था कि कई समस्याओं वे गणित में मुठभेड़ कि जैविक माध्यमिक ज्ञान है ‘ गैर दिनचर्या है ।
- मार्क McCourt (२०१८) महारत श्रृंखला के लिए अपने शिक्षण में एक गणित शिक्षक लिखते हैं, ‘ कई शिक्षकों को यह एक असहज लगता है-शायद यह भी विसंगत-प्रक्रिया ‘ के रूप में एक है कि बहुत पहले सीखने से संबंधित है के रूप में ‘ व्यवहार चरण योजना के बजाय नए विचार है, लेकिन यह महत्वपूर्ण है ऐसा करने के लिए अगर हम सीखने, समझने और दीर्घकालिक याद में इष्टतम लाभ के बारे में लाना चाहते हैं । क्या इस बदतर आईडी कि Burkhadt इस बारे में लगभग 30 साल पहले १९८० (Treilibs, Burkhardt और कम, १९८०) में लिखा है बनाता है । और अभी तक प्राथमिक गणित सबक में और देश के नीचे, 20 मिनट के अंतरिक्ष में, हम एक बच्चे के माध्यम से सही प्रवाह से समस्या को हल करने के लिए स्थानांतरित कर सकते हैं ।
- गणित में समस्या हल करने की क्षमता के साथ हमारे छात्रों को सफलतापूर्वक लैस करने के लिए, हमें पता है और निम्नलिखित करने की जरूरत है:
- ‘ का एक पहलू समस्या हल ‘ एक सहज सदियों से विरासत में मिली क्षमता है-कुछ दूसरों की तुलना में अधिक होगा ।
- समस्या को सुलझाने के डोमेन भर में स्थानांतरण नहीं है-सिर्फ इसलिए कि मैं एक में समस्याओं का समाधान कर सकते है मतलब है कि तुम दूसरों में नहीं कर सकते हैं ।
- सिखाना और संदर्भों की एक सीमा में जैविक माध्यमिक अवधारणाओं के massed अभ्यास के लिए अवसर प्रदान-उंहें भी जल्दी पर कदम नहीं है ।
- सुनिश्चित करें कि गणितीय शब्दावली अच्छी तरह से sequenced है, स्पष्ट रूप से सिखाया और महारत हासिल
- समस्या के समाधान से अलग तर्क-वितर्क समस्या समाधान की अपेक्षा है ।
- जब समस्या को हल करने के लिए सामग्री का चयन, यह साल पहले की एक जोड़ी से चुनें (मैं जानता हूं कि यह पाठ्यक्रम की कमी के कारण मुश्किल है)
- मुझे आशा है कि यह आप सोचा के लिए कुछ खाना दिया है और शायद कर सकते है आप अपने अध्यापन पर विचार जब गणितीय समस्या को सुलझाने के बारे में सोच रही है । मैं एक भाग 3 गर्मियों में ऊपर की व्याख्या करने के लिए मैं क्या में समस्या के अपने शिक्षण के लिए संबंध को हल करने की उंमीद है ।
- ग्रंथसूची:
- तरीके मॉडलिंग सिखाने के लिए-एक ५० साल के अध्ययन, नॉटिंघम विश्वविद्यालय, पर पहुंचा । बच्चों की अनुभूति में विकास और संस्कृति का प्रतिबिंब: गणितीय विकास और अनुदेश के लिए निहितार्थ । अमेरिकी मनोवैज्ञानिक: स्कूलों हमारे बच्चों की जरूरत बनाना: क्यों हम सही कर रहे है अब काम नहीं है, और क्या हम Inst कर सकते हैं: सीखना विज्ञान इंटरनेशनल
- . गणितीय मॉडलिंग में निर्माण प्रक्रियाओं । नॉटिंघम [इंग्लैंड], मैथमेटिकल एजुकेशन के लिए शेल सेंटर ।
- Willingham, डैनियल टी (२०१०) । क्यों छात्रों को स्कूल की तरह नहीं है?: एक संज्ञानात्मक वैज्ञानिक मन कैसे काम करता है और क्या यह कक्षा के लिए इसका मतलब के बारे में सवालों के जवाब
- Ramble #7 मैं कैसे संरचना मेरे गणित सबक: अभ्यास में डाल अनुसंधान Ramble: (चेतावनी खेल सिंहासन विफल)
- “पर एक विचार Ramble समस्या के साथ समस्या (गणित में) को हल #8”
- यह एक उत्कृष्ट रिपोर्ट है । के दौरान ३५ प्राथमिक स्कूलों में अध्यापन वर्ष, मैं जानता हूं कि बच्चों के तर्क में एक अच्छा ग्राउंडिंग की जरूरत है (इसके संबद्ध सोच verbalise करने की क्षमता के साथ) में आदेश समस्या को गणित में हल । जब समस्या के शिक्षण पहलुओं को हल करने के साथ सामना, मैं नियमित रूप से बताया गया था कि गणित पाठ्यक्रम के ‘ कवरेज ‘ बहुत धीमी थी, जब वास्तव में बच्चों को कौशल है कि उन्हें तर्क लागू करने के लिए सक्षम होगा honing थे । महान काम करते हैं । आप इसे पढ़ने के लिए एक व्यापक शिक्षण दर्शकों की जरूरत है । शायद तब शिक्षक रोबोट के अभ्यास पर बच्चों का समय बर्बाद करना बंद कर सकते हैं, जहां वे ‘ दिन के लिए ‘ सीखते है और वास्तव में कभी समझ नहीं पाते । हम भी गणित के बजाय यह डर के साथ एक प्यार के साथ गणितज्ञों और/
- उपर्युक्त आर्टिकल में गणितीय समस्या को हल करना (Mathematical problem solving) के बारे में बताया गया है।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.
