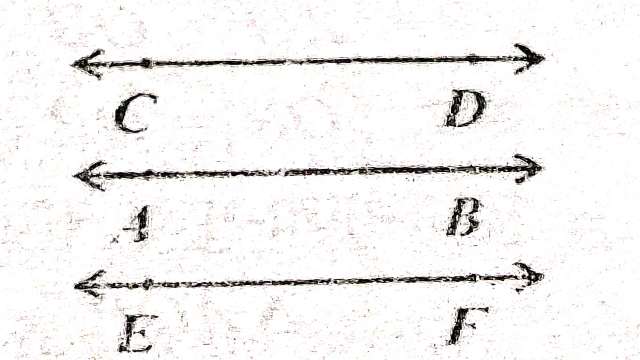1.बिन्दुपथ और संगामी रेखाएं (Loci And Concurrent Lines)-

बिन्दुपथ और संगामी रेखाएं (Loci And Concurrent Lines) में बिन्दुपथ का अर्थ होता है बिन्दुओं का मार्ग। जिसका अर्थ है कि गतिमान बिन्दु का बिन्दुपथ वह वक्र है,जो दिए गए प्रतिबन्धों के अधीन अनुरेखित हो।फिर भी ज्यामितीय दृष्टिकोण से उपर्युक्त कथन से विस्तृत है।हम बिन्दुपथ को अधिक यथार्थत: निम्नलिखित उदाहरणों के द्वारा समझ सकते हैं।

(1.)यदि समतल में एक बिन्दु इस प्रकार गतिमान है कि वह एक निश्चित बिन्दु से सदैव अचर दूरी पर हो तो इस बिन्दु का बिन्दुपथ एक वृत्त होगा जिसका केन्द्र निश्चित बिन्दु O तथा त्रिज्या निश्चित दूरी a होगी।
(2.)यदि किसी समतल में एक बिन्दु इस प्रकार गतिमान है कि इसकी दूरी एक दी गई रेखा AB से सदैव समान रहे तो इस बिन्दु का बिन्दुपथ रेखा AB के दोनों ओर दो समान्तर रेखाएं CD और EF होगी।

(3.)गोला (sphere) समष्टि में एक बिन्दु का बिन्दुपथ है जो इस प्रकार गमन करता है कि इसकी दूरी (त्रिज्या) निश्चित बिन्दु (केन्द्र) से सदैव समान रहती है।
उपर्युक्त उदाहरणों से हम इस निष्कर्ष पर पहुंचते हैं कि जब कोई बिन्दु कुछ प्रतिबन्धों के अन्तर्गत गतिमान होता है,तो वह ज्यामितीय आकृति को अनुरेखित करता है।यह ज्यामितीय आकृति ही बिन्दु का बिन्दुपथ कहलाती है।
ज्यामिति में बिन्दु भौतिक वस्तु नहीं है।यदि हम बिन्दु को एक अतिसूक्ष्म परिमाण के रूप में निरूपित करें तो हम कह सकते हैं कि किन्हीं प्रतिबन्धों के अन्तर्गत किसी बिन्दु का बिन्दुपथ वह ज्यामितीय आकृति है जो उसको निरूपित करने वाले कण के द्वारा आनुरेखित होता है।
अतः किन्हीं प्रतिबन्धों के अन्तर्गत एक बिन्दु का बिन्दुपथ वह ज्यामितीय आकृति है जिसका प्रत्येक बिन्दु दिए गए प्रतिबन्धों को सन्तुष्ट करता है।
किसी भी बिन्दुपथ में निम्नलिखित निष्कर्षो का समावेश होता है-
(a) दिए गए प्रतिबन्धों को सन्तुष्ट करने वाला प्रत्येक बिन्दु बिन्दुपथ पर स्थित है और
(b) बिन्दुपथ का प्रत्येक बिन्दु दिए गए प्रतिबन्धों को सन्तुष्ट करता है।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:-Height and Distance in Trigonometry

2.दिए गए दो बिन्दुओं से समदूरस्थ बिन्दु (Points Equidistant From Two Given Points)-

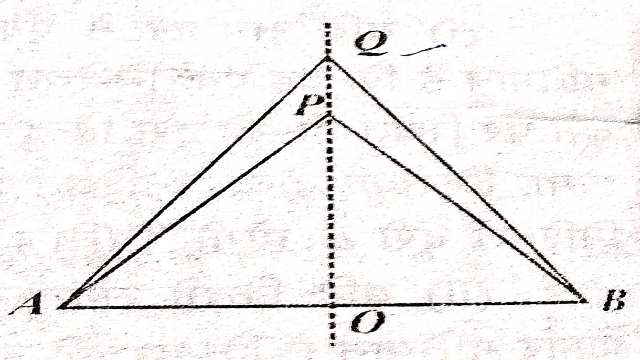
प्रमेय (Theorem):1.किन्हीं दो बिन्दुओं से समान दूरी पर स्थित बिन्दुओं का बिन्दुपथ दिए हुए बिन्दुओं को मिलाने वाली रेखा का लम्ब समद्विभाजक होता है।

चित्र में P एक ऐसा बिन्दु है जो A और B से समान दूरी पर है।P को AB के मध्य-बिन्दु O से मिलाया।
$\triangle AOP$ एवं $\triangle BOP$ में
AP=BP (दिया है)
AO=OB (रचना से)
और OP=OP (उभयनिष्ठ भुजा)
भुजा-भुजा-भुजा सर्वांगसमता गुणधर्म से (SSS Property)

$\triangle AOP \cong \triangle BOP$
अतः $\angle AOP = \angle BOP$ (CPCT से)……(1)
$\angle AOP + \angle BOP=180°$(रैखिक कोण युग्म)
(1) व (2) से-

$\angle AOP = \angle BOP=90°$
अर्थात् OP रेखा AB का लम्ब-समद्विभाजक है।
अब इसी प्रकार लम्ब समद्विभाजक पर कोई बिन्दु Q लेकर QA और QB को मिलाने पर हम देखते हैं कि QA=QB है और यह लम्ब समद्विभाजक OQ पर स्थित प्रत्येक बिन्दु के लिए सत्य होगा।

3.दो प्रतिच्छेदी रेखाओं से समदूरस्थ बिन्दु (Point Equidistant From Two Intersecting Lines),दो प्रतिच्छेदी रेखाओं से समदूरस्थ बिन्दुओं का बिन्दुपथ (Locus of points equidistant from two intersecting lines),दो रेखाओं से समदूरस्थ बिन्दुओं का बिन्दुपथ (Locus of points equidistant from two lines)-

प्रमेय(Theorem):2.दो प्रतिच्छेदी रेखाओं से समान दूरी पर स्थित बिन्दुओं का बिन्दुपथ उन दोनों रेखाओं से बने कोणों का समद्विभाजक होता है।

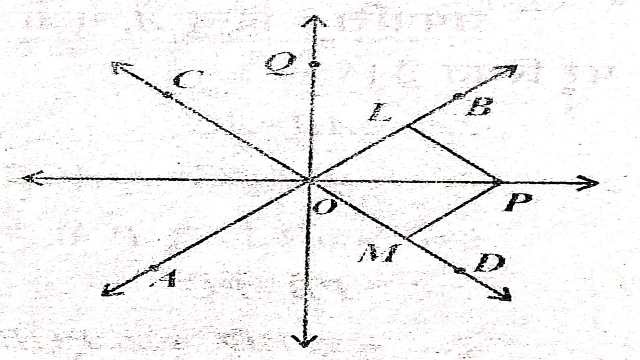
चित्र में दो रेखाएं AB और CD हैं जो परस्पर O पर प्रतिच्छेद करती हैं। हमें बिन्दु P का बिन्दुपथ ज्ञात करना है,जब यह बिन्दु रेखाओं AB और CD से समान दूरी पर हो।
माना कि रेखा AB और CD से बिन्दु P की दूरी d है, अतः PL=PM=d।यदि d=0 हो तो बिन्दु P दोनों रेखाओं AB और CD पर स्थित होगा,P और O सम्पाती होंगे अर्थात् O भी बिन्दु P के बिन्दुपथ का एक बिन्दु होगा।
यदि $d \neq 0$ हो तो 

$\triangle PLO$ एवं $\triangle PMO$ में
PL=PM (दिया है)
OP=OP (उभयनिष्ठ भुजा)

$\angle PLO = \angle PMO=90°$
समकोण-कर्ण-भुजा सर्वांगसमता गुणधर्म से (RHS Congruence Property)

$\triangle PLO \cong \triangle PMO$
अतः $\angle POL = \angle POM$
(सर्वांगसम त्रिभुजों के संगत कोण बराबर होते हैं)
अतः OP ,$\angle MOL$ का समद्विभाजक है। इसलिए $\angle MOL$ का कोण समद्विभाजक OP बिन्दुपथ का एक भाग है।इसी प्रकार $\angle BOC$ का कोण समद्विभाजक OQ भी बिन्दुपथ का एक भाग है।बिन्दु P रेखा AB और CD दोनों से समान दूरी पर है।

4.बिन्दुपथ और संगामी रेखाएं के उदाहरण (Loci And Concurrent Lines Examples), गणित में बिन्दुपथ के उदाहरण (Locus maths examples)-

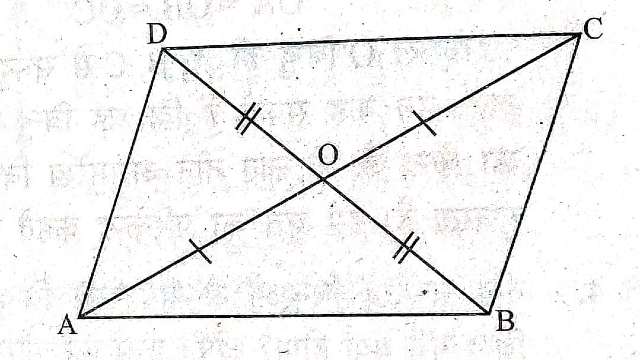
Example-1.एक चतुर्भुज के विकर्ण एक-दूसरे को समद्विभाजित करते हैं।सिद्ध कीजिए कि वह चतुर्भुज समांतर चतुर्भुज है।

Solution-दिया है (Given): ABCD एक चतुर्भुज है जिसमें विकर्ण O बिन्दु पर प्रतिच्छेद करते हैं।तथा OA=OC एवं OB=OD ।
सिद्ध करना है (To Prove):ABCD एक समान्तर चतुर्भुज है।
उपपत्ति (Proof): $\triangle AOB$ तथा $\triangle COD$ में
OA=OC (दिया है)
$\angle AOB = \angle COD$(शीर्षाभिमुख कोण)
OB=OD (दिया है)
भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से (SAS Congruence Property)

$\triangle AOB \cong \triangle COD$
$\angle OAB = \angle OCD$(CPCT से)
ये दोनों एकान्तर कोण हैं $\because  AB \parallel CD$
इसी प्रकार $AD \parallel BC$ होगी।
अतः ABCD एक समान्तर चतुर्भुज है।
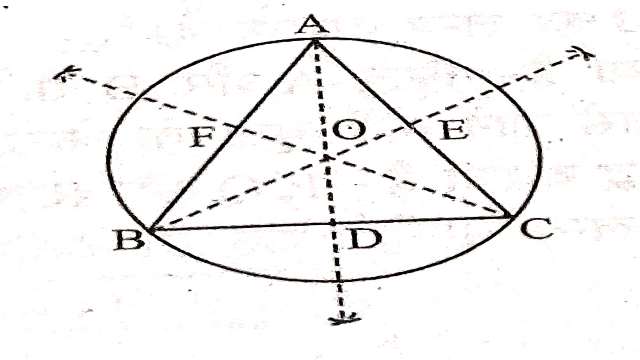
Example-2.तीन असमरेख बिन्दुओं A,B और C से समदूरस्थ बिन्दुओं का बिन्दुपथ क्या होगा? अपने उत्तर का कारण स्पष्ट कीजिए।

Solution– दिया है (Given): तीन असमरेख बिन्दु A,B तथा C हैं।
सिद्ध करना है (To Prove): A,B तथा C से समदूरस्थ बिन्दुओं का बिन्दुपथ ज्ञात करना है।
रचना (Construction):AB,BC तथा CA को मिलाया तथा AB,BC,CA के लम्ब समद्विभाजक OF,OD,OE खींचे जो O पर प्रतिच्छेद करते हैं।
उपपत्ति (Proof): $\because$ O,BC के लम्ब समद्विभाजक पर स्थित है।
$\therefore$  OB=OC ……..(1)
इसी प्रकार OA=OB …….(2)
समीकरण (1) व (2) से-
OA=OB=OC
$\therefore$ केवल O बिन्दु ही A,B,C से समदूरस्थ है।
अतः हम कह सकते हैं कि वह बिन्दु उस वृत्त का केन्द्र है जो ज्ञात तीन असमरेख बिन्दुओं से गुजरता है।इसे वृत्त का परिकेन्द्र कहते हैं।
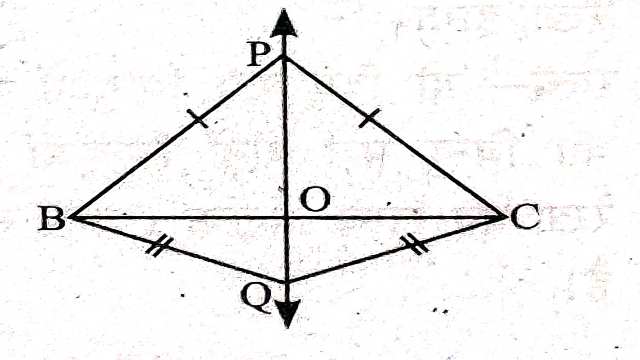
Example-3.दी गई आकृति में उभयनिष्ठ आधार BC पर रेखा BC के विपरीत ओर दो समद्विबाहु त्रिभुज $\triangle PBC$ और $\triangle QBC$ स्थित हैं। सिद्ध कीजिए कि P और Q को मिलाने वाली रेखा BC को समकोण पर समद्विभाजित करती है।

Solution-दिया है (Given): आधार BC के विपरीत दोनो ओर बने दो समद्विबाहु त्रिभुज दिए हैं जिनमें PB=PC तथा OQ=QC है तथा PQ तथा BC बिन्दु O पर प्रतिच्छेद करती हैं।
सिद्ध करना है (To Prove):BO=CO तथा $\angle BOP=90°$
उपपत्ति (Proof): $\triangle PBQ$ तथा $\triangle PCQ$ में
PB=PC (दिया है)
BQ=CQ (दिया है)
PQ=PQ (उभयनिष्ठ भुजा)
भुजा-भुजा-भुजा सर्वांगसमता गुणधर्म से (SSS Congruence Property)

$\triangle PBQ \cong \triangle PCQ$
$\therefore  \angle BPQ= \angle CPQ$(CPCT से)

$\angle BPO= \angle CPO$…(1)
अब $\triangle BPO$ तथा $\triangle CPO$ में
BP=CP (दिया है)
$\angle BPO= \angle CPO$[(1) से]
PO=PO (उभयनिष्ठ भुजा)
भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से (By SAS Congruence Property)

$\triangle BPO \cong \triangle CPO$
$\Rightarrow  BO=CO$ (CPCT से)
तथा $\angle BOP= \angle COP$
परन्तु $\angle BOP+ \angle COP=180°$(रैखिक कोण युग्म)

अतः $\angle BOP=90°$
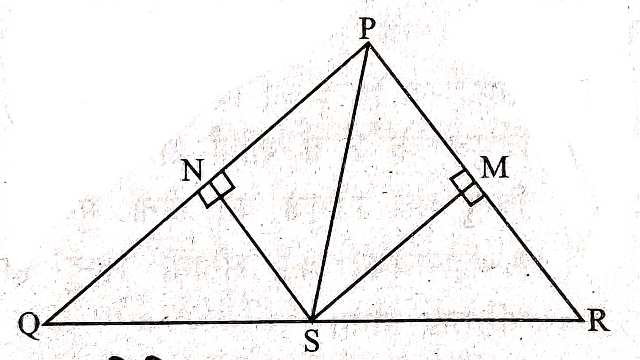
Example-4.दी गई आकृति में, उभयनिष्ठ आधार QR पर एक ही ओर दो समद्विबाहु त्रिभुज $\triangle PQR$ और $\triangle SQR$ स्थित हैं। सिद्ध कीजिए कि SP रेखा,QR की लम्ब अर्द्धक है।

Solution-दिया है (Given): आधार QR एक ही ओर दो समद्विबाहु $\triangle PQR$ और $\triangle SQR$ हैं।
सिद्ध करना है (To Prove):SP रेखा QR की लम्ब अर्द्धक है।
उपपत्ति (Proof): $\triangle QPS$ तथा $\triangle RPS$ में
QP=RP (दिया है)
QS=RS (दिया है)
PS=PS (उभयनिष्ठ भुजा)
भुजा-भुजा-भुजा सर्वांगसमता गुणधर्म से (By SSS Congruence Property)

$\triangle QPS \cong \triangle RPS$
$\Rightarrow  \angle QSP = \angle RSP$ (CPCT से)…..(1)
अब $\triangle QOS$ तथा $\triangle ROS$ में
QS=RS (दिया है)
$\angle QSO = \angle RSO$[(1) से]
SO=SO (उभयनिष्ठ भुजा)
भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से (By SAS Congruence Property)

$\triangle QOS \cong \triangle ROS$
$\Rightarrow QO=RO$(CPCT से)
एवं $\angle QOS = \angle ROS$(CPCT से)
परन्तु $\angle QOS + \angle ROS=180°$(रैखिक कोण युग्म)
अतः $\angle QOS=90°$
अतः SP रेखा QR की लम्ब अर्द्धक है।
Example-5.दी गई आकृति में, $\angle P$ अर्द्धक PS,भुजा QR को S बिन्दु पर प्रतिच्छेद करता है। $SN \perp PQ$ एवं $SM \perp PR$ खींचे गए हैं। सिद्ध कीजिए कि SN=SM

Solution-दिया है (Given):का अर्द्धक PS है तथा $SN \perp PQ$ एवं $SM \perp PR$
सिद्ध करना है (To Prove):SN=SM
उपपत्ति (Proof): $\triangle SNP$ तथा $\triangle SMP$ में

$\angle SNP=\angle SMP=90°$
$\angle SPN=\angle SPM$(दिया है)
PS=SP (उभयनिष्ठ भुजा)
भुजा-कोण-भुजा सर्वांगसमता गुणधर्म से (By SAS Congruence Property)

$\triangle SNP \cong \triangle SMP$
अतः SN=SM (CPCT से)
उपर्युक्त उदाहरणों के द्वारा बिन्दुपथ और संगामी रेखाएं (Loci And Concurrent Lines) को समझ सकते हैं।

5.संगामी रेखाएं (Concurrent Lines):-

तीन या तीन से अधिक रेखाएं संगामी कहलाती है यदि वे सभी किसी एक सर्वनिष्ठ बिंदु से गुजरती हों। सर्वनिष्ठ बिंदु को रेखाओं का संगमी बिन्दु कहते हैं।
त्रिभुज के किसी शीर्ष और सम्मुख भुजा के मध्य बिंदु को मिलाने वाले रेखाखंड को त्रिभुज की माध्यिका कहते हैं। त्रिभुज के किसी शीर्ष से सम्मुख भुजा पर डाले गए लंब को शीर्षलंब कहते हैं।इस प्रकार किसी त्रिभुज में तीन माध्यिकाएं और तीन शीर्षलंब होते हैं।किसी भी त्रिभुज में कोणों के समद्विभाजक,शीर्षलंब,भुजाओं के लम्ब-समद्विभाजक एवं माध्यिकाएं संगामी होती है।
प्रमेय (Theorem):3.त्रिभुज की भुजाओं के लम्ब समद्विभाजक संगामी होते हैं।

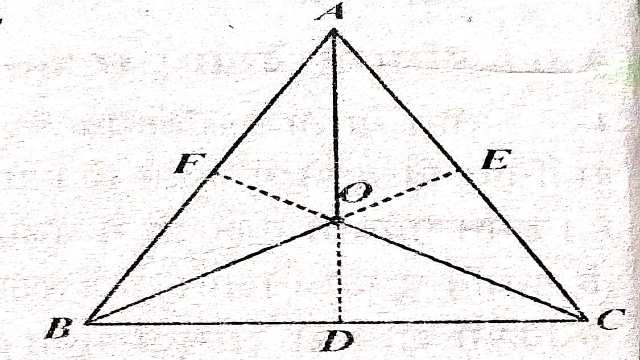
दिया है (Given): $\triangle ABC$ में भुजा AB एवं AC के लम्ब-समद्विभाजक बिंदु O पर मिलते हैं और OD भुजा BC पर लम्ब हो।
सिद्ध करना है (To Prove):OD भुजा BC का लम्ब समद्विभाजक है।
रचना (Construction):OA,OB और OC को मिलाया।
उपपत्ति (Proof):OE एवं OF क्रमशः AC एवं AB के लम्ब-समद्विभाजक हैं अतः OA=OB=OC
OD,भुजा BC पर लम्बवत है अतः OB=OC
OD,भुजा BC का लम्ब समद्विभाजक है।
प्रमेय(Theorem):4.त्रिभुज के कोणों के समद्विभाजक संगामी होते हैं।

दिया है (Given): $\triangle ABC$ में $\angle B$ एवं $\angle C$ के समद्विभाजक बिन्दु O पर मिलते हैं।
सिद्ध करना है (To Prove):OA, $\angle A$ को समद्विभाजित करता है।
रचना (Construction): चित्र में,O से लम्ब OD,OE और OF खींचे।
उपपत्ति (Proof):OB एवं OC क्रमशः $\angle B$ एवं $\angle C$ के समद्विभाजक हैं अतः
OD=OF …….(1)
OD=OE ……..(2)
(1) और (2) से-
OE=OF
अतः O,AB और AC से समान दूरी पर स्थित हैं।
अर्थात् OA,$\angle A$ को समद्विभाजित करता है।
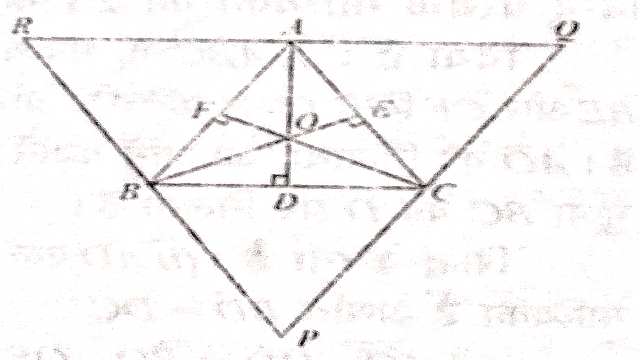
प्रमेय (Theorem):5.त्रिभुज के तीनों शीर्षलम्ब संगामी होते हैं।

दिया है (Given):$\triangle ABC$ के AD एवं CF शीर्षलम्ब है।
सिद्ध करना है (To Prove):AD,BE एवं CF एक ही बिन्दु से होकर जाते हैं।
रचना (Construction):चित्र के अनुसार समान्तर रेखाएं खींचकर $\triangle PQR$ बनाया।
उपपत्ति (Proof): चतुर्भुज BACR में,
$AC \parallel RB$(रचना से)
और $BC \parallel RA$(रचना से)
$\therefore$ BCAR एक समान्तर चतुर्भुज है।
अतः RA=BC ……..(1)
इसी प्रकार ABCQ भी एक समान्तर चतुर्भुज है।
अतः AQ=BC ……(2)
(1) और (2) से-
AR=AQ …………..(3)
एवं $AD \perp BC$ और $BC \parallel QR$
अतः$AD \perp QR$…..(4)
समीकरण (3) और (4) से,AD भुजा QR का लम्ब समद्विभाजक है।इसी प्रकार BE एवं CF क्रमशःPR एवं PQ के लम्ब-समद्विभाजक हैं।इस प्रकार AD,BE और CF,$\triangle PQR$ की भुजाओं के लम्ब समद्विभाजक हैं। अतः AD,BE और CF एक ही बिन्दु से होकर जाते हैं।
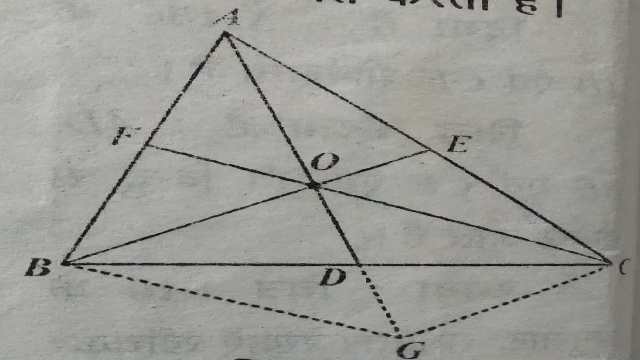
प्रमेय (Theorem):6.त्रिभुज की माध्यिकाएं एक ही बिन्दु से होकर जाती हैं और यह बिन्दु प्रत्येक माध्यिका को 2:1 के अनुपात में विभाजित करता है।

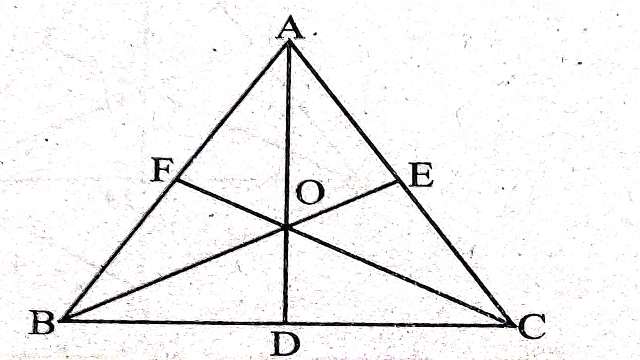
दिया है (Given): $\triangle ABC$ में माध्यिकाएं BE और CF बिन्दु O पर प्रतिच्छेद करती हैं।AO को मिलाया जो आगे बढ़ाने पर भुजा BC को D पर मिलता है।
सिद्ध करना है (To Prove):(1) AD एक माध्यिका है अर्थात् BD=DC
(2) AO:OD=BO:OE=CO:OF=2:1
रचना (Construction):AD को G तक इस प्रकार आगे बढ़ाया कि AO=OG हो।BG और CG को मिलाया।
उपपत्ति (Proof):(1.)हम जानते हैं कि किसी त्रिभुज की दो भुजाओं के मध्य बिन्दुओं को मिलाने वाला रेखाखण्ड तीसरी भुजा के समान्तर और उसका आधा होता है।
$\triangle ABG$ में,F एवं O क्रमशः AB और AG के मध्यबिन्दु हैं।
अतः $OF \parallel GB.....(1) \\ OF=\frac{1}{2} GB$….(2)

इसी प्रकार $\triangle ACG$ में,E एवं O क्रमशः AC और AG के मध्यबिन्दु हैं।

अतः $OE \parallel GC.....(3) \\ OE=\frac{1}{2} GC$….(4)
समीकरण (1) और (3) से,BOCG एक समान्तर चतुर्भुज है जिसकी भुजाएं $BG \parallel OC$ और $GC \parallel BO$ हैं।समान्तर चतुर्भुज के विकर्ण BC एवं OG परस्पर D पर समद्विभाजित करते हैं।
अतः BD=DC
अर्थात् AD, शीर्ष A से खींची गई माध्यिका है।
(2.)D,समान्तर चतुर्भुज BOCG के विकर्णों का प्रतिच्छेद बिन्दु है, अतः
OD=DG

$\Rightarrow  OD=\frac{1}{2} OG$…..(5)
परन्तु रचना से AO=OG ……(5)
समीकरण (5) और (6) से- $OD=\frac{1}{2} AO \\ \Rightarrow \frac{AO}{OD}=\frac{2}{1} \\ \Rightarrow AO:OD=2:1$
इसी प्रकार BO:OE=2:1 और CO:OF=2:1
अर्थात् AO:OD=BO:OE=CO:OF=2:1
विशेष:(1.)त्रिभुज की भुजाओं के लक्ष्म-समद्विभाजकों का संगामी बिंदु त्रिभुज का परिकेंद्र (Circumcentre) कहलाता है। परिकेंद्र की त्रिभुज के तीनों शीर्षों से दूरी समान होती है।इस समान दूरी को त्रिभुज की परित्रिज्या (Circumradius) और वृत्त को परिवृत्त (Circumcircle) कहते हैं।
(2.)त्रिभुज के कोणों समद्विभाजकों के संगामी बिंदु को त्रिभुज का अंतः केंद्र (Incentre) कहते हैं।अन्त:केन्द्र की त्रिभुज की भुजाओं से दूरी समान होती है।अन्त:केंद्र से किसी भुजा पर खींचे गए लम्ब को त्रिज्या मानकर खींचा गया वृत्त,त्रिभुज की तीनो भुजाओं को स्पर्श करता है।इस वृत्त को अन्त: वृत्त (Incircle) कहते हैं और इसकी त्रिज्या को अन्त: त्रिज्या (Inradius) कहते हैं।
(3.) त्रिभुज के तीनों शीर्षलम्बों के संगामी बिन्दु को त्रिभुज का लम्बकेन्द्र (Orthocentre) कहते हैं।
(4.) त्रिभुज की माध्यिकाओं के संगामी बिन्दु को त्रिभुज का केन्द्रक (Centroid) कहते हैं।

6.बिन्दुपथ और संगामी रेखाएं के उदाहरण (Loci And Concurrent Lines Examples),बिन्दुपथ की समस्याएं हल सहित (Locus problems with solutions)-

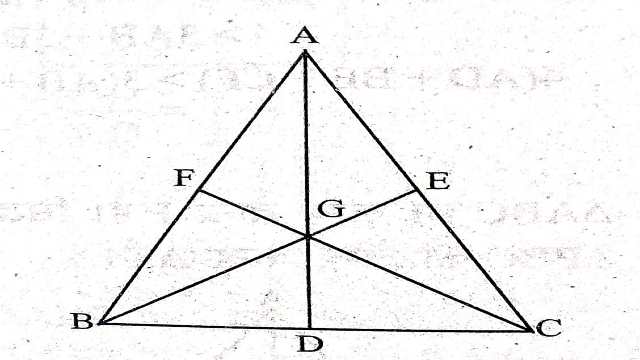
Example-6.एक त्रिभुज ABC में,माध्यिकाएं AD,BE और CF बिन्दु G पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि

$AD+BE>\frac{3}{2} AB$

Solution-दिया है (Given):AD,BE और CF,की तीन माध्यिकाएं हैं जो बिन्दु G पर प्रतिच्छेद करती हैं।
सिद्ध करना है (To Prove):$AD+BE>\frac{3}{2} AB$
उपपत्ति (Proof):BG+GE=BE

$\frac{BG}{BG}+\frac{GE}{BG}=\frac{BE}{BG} \\ \Rightarrow 1+\frac{GE}{BG}=\frac{BE}{BG} (GE:BG=1:2) \\ \Rightarrow 1+\frac{1}{2}=\frac{BG}{BG} (\therefore \frac{3}{2}=\frac{BE}{BG}) \\ \Rightarrow BE=\frac{3}{2}BG$…(1)
इसी प्रकार AG+GD=AD

$\frac{AG}{AG}+\frac{GD}{AG}=\frac{AD}{AG} (AG:GD=2:1) \\ \Rightarrow 1+\frac{1}{2}=\frac{AD}{AG} (\therefore \frac{3}{2}=\frac{AD}{AG}) \\ \Rightarrow AD=\frac{3}{2}AG$…(2)
समीकरण (1) व (2) को जोड़ने पर-

$AD+BE=\frac{3}{2}AG+\frac{3}{2}BG \\ \Rightarrow AD+BE=\frac{3}{2} (AG+BG)$….(3)
किन्तु $\triangle AGB$ में
AG+BG>AB

$\frac{3}{2} (AG+BG)>\frac{3}{2}AB$…..(4)
समीकरण (3) व (4) से-

$AD+BE>\frac{3}{2}AB$
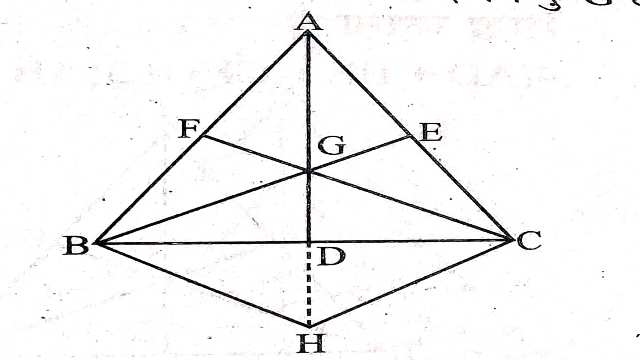
Example-7.सिद्ध कीजिए कि त्रिभुज की दो माध्यिकाओं का योग तीसरी माध्यिका से अधिक होता है।

दिया है (Given):AD,BE और CF,$\triangle ABC$ की तीन माध्यिकाएं हैं जिनका प्रतिच्छेद बिन्दु G है।
सिद्ध करना है (To Prove):दो माध्यिकाओं का योग>तीसरी माध्यिका अर्थात्
AD+BE>CF
BE+CF>AD
AD+CF>BE
रचना (Construction):GD को H तक इस प्रकार बढ़ाया कि GD=DH तथा H को B व C से मिलाया।
उपपत्ति (Proof):GD=DH
अतः D,GH तथा BC का मध्यबिन्दु है।
BC तथा GH परस्पर समद्विभाजित करते हैं।
BGCH एक समान्तर चतुर्भुज है।
CH=BG तथा BH=GC
$\triangle GHC$ में,CH+GH>GC
BG+GH>GC …….(1)
CH=BG
$\because GF\parallel BH$ (समान्तर चतुर्भुज की सम्मुख भुजाएं)
$\therefore  \triangle ABH$ में $FG \parallel BH$ (F,AB का मध्यबिन्दु है)
G,AH का मध्यबिन्दु होगा।
AG=GH …..(2)
समीकरण (1) और (2) से-
BG+AG>GC

$\Rightarrow \frac{3}{2} BE+\frac{3}{2} AD>\frac{3}{2} CF \\ \Rightarrow \frac{3}{2} (BE+AD)>\frac{3}{2} CF$
BE+AD>CF
इसी प्रकार BE+CF>AD और AD+CF>BE
Example-8.एक में,माध्यिकाएं AD,BE और CF बिन्दु G पर प्रतिच्छेद करती है। सिद्ध कीजिए कि 4(AD+BE+CF)>3(AB+BC+CA)

Solution-दिया है (Given):की माध्यिकाएं AD,BE और CF का प्रतिच्छेद बिन्दु O है।
सिद्ध करना है (To Prove):4(AD+BE+CF)>3(AB+BC+CA)
उपपत्ति (Proof):माध्यिकाओं का प्रतिच्छेद बिन्दु O है।
AO:OD=2:1 

$\frac{OD}{AO}=\frac{1}{2} \\ \Rightarrow 1+\frac{OD}{AO}=\frac{1}{2}+1 \\ \Rightarrow \frac{OA+OD}{AO}=\frac{3}{2} \Rightarrow \frac{AD}{AO}=\frac{3}{2} \\ \Rightarrow AD=\frac{3}{2}AO...(1)$
इसी प्रकार $BE=\frac{3}{2}BO.....(2)$
और $CF=\frac{3}{2}CO......(3)$
समीकरण (1) और (2) से-

$AD+BE=\frac{3}{2}(AO+BO)$
किन्तु $\triangle AOB$ में
AO+BO>AB

$\Rightarrow AD+BE>\frac{3}{2}AB$
2(AD+BE)>3AB …..(4)
समीकरण (2) और (3) को जोड़ने पर-

$BE+CF=\frac{3}{2}(BO+CO) \\ \Rightarrow BE+CF>\frac{3}{2}BC(\because BO+CO>BC) \\ \Rightarrow 2(BE+CF)>\frac{3}{2}BC.....(5)$
समीकरण (1) व (3) को जोड़ने पर-
2(AD+BE)+2(BE+CF)+2(CF+AD)>3AB+3BC+3CA
4(AD+BE+CF)>3(AB+BC+CA)
Example-9. $\triangle ABC$ समद्विबाहु त्रिभुज है जिसमें AB=BC,BC का मध्यबिन्दु है। सिद्ध कीजिए कि परिकेन्द्र,अंत:केन्द्र,लम्बकेन्द्र तथा केन्द्रक सभी AD रेखा पर स्थित हैं।

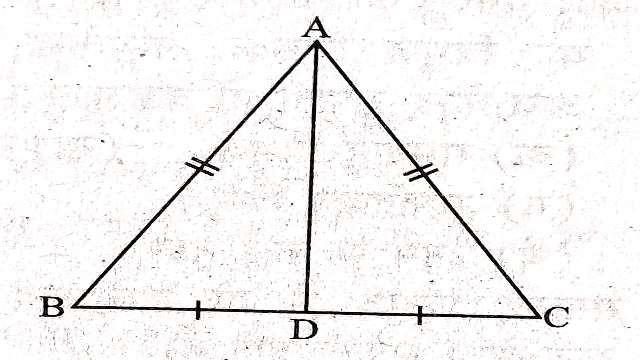
दिया है (Given):$\triangle ABC$ एक समद्विबाहु त्रिभुज है जिसमें AB=AC तथा BC का मध्यबिन्दु D है।
सिद्ध करना है (To Prove):परिकेन्द्र,अन्त:केन्द्र लम्बकेन्द्र तथा केन्द्रक सभी AD रेखा पर स्थित हैं।
उपपत्ति (Proof): $\triangle ADB$ तथा $\triangle ADC$ में
AB=AC (दिया है)
BD=CD (बिन्दु D,BC का मध्यबिन्दु है)
तथा AD=AD (उभयनिष्ठ भुजा)
भुजा-भुजा-भुजा सर्वांगसमता गुणधर्म से (By SSS Congruence Property)

$\triangle ADB \cong \triangle ADC$
$\Rightarrow \angle BDA=\angle CDA$ (CPCT से)
परन्तु $\angle BDA+\angle CDA=180°$(रैखिक कोण युग्म)

$\therefore  \angle BDA=90°$
अब AD,BC का लम्ब अर्द्धक है इसलिए परिकेन्द्र AD पर होगा।
$\angle BAD=\angle CAD$(CPCT से)

[ $\because  \triangle ADB \cong \triangle ADC$]
$\therefore AD,\angle BAC$ का अर्द्धक है अतः अन्त:केन्द्र भी AD पर होगा।
$\because AD \perp BC$ है अतः लम्बकेन्द्र भी AD पर होगा।
अब अन्त में AD,माध्यिका है अतः केन्द्रक भी AD रेखा पर स्थित होगा।
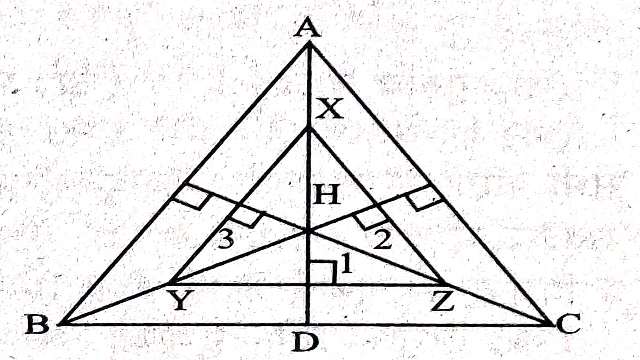
Example-10.का लम्बकेन्द्र H है।AH,BH और CH में मध्यबिन्दु क्रमशः X,Y और Z हैं। सिद्ध कीजिए कि $\triangle XYZ$ का लम्बकेन्द्र भी H है।

Solution-दिया है (Given): $\triangle ABC$ का लम्बकेन्द्र भी H है।AH,BH और CH में मध्यबिन्दु क्रमशः X,Y और Z हैं।
सिद्ध करना है (To Prove): $\triangle XYZ$ का लम्बकेन्द्र भी H है।
उपपत्ति (Proof): $\triangle ABC$ का लम्बकेन्द्र H है (दिया है)
$\triangle ABH$ में X,AH का मध्यबिन्दु है तथा Y,BH का मध्यबिन्दु है।
$XY \parallel AB$ होगी।(मध्यबिन्दु प्रमेय से)
इसी प्रकार $YZ \parallel BC$ एवं $ZX \parallel AC$ होगी।
अब संगतकोण बराबर होने से $\angle 1=\angle 2=\angle 3$
(प्रत्येक 90°)
अतः $\triangle XYZ$ का लम्बकेन्द्र भी H है।
Example-11.एक $\triangle ABC$ में माध्यिकाएं AD,BE और CF बिन्दु G पर प्रतिच्छेद करती है।यदि AG=6cm,BE=9cm और GF=4.5cm हो,तो GD,BG और CF ज्ञात कीजिए।

Solution-$\triangle ABC$ में AD,BC की माध्यिका है और माध्यिकाओं का प्रतिच्छेद बिन्दु G है।

$\frac{AG}{GD}=\frac{2}{1}$
किन्तु AG=6cm

$\frac{6}{GD}=\frac{2}{1} \\ GD=\frac{6}{2}$
GD=3cm
$\triangle ABC$ में BE,AC की माध्यिका है।

$\frac{BG}{GE}=\frac{2}{1}$
किन्तु BE=9cm

$\frac{BG}{BE-BG}=\frac{2}{1} \\ \Rightarrow \frac{BG}{9-BG}=\frac{2}{1} \\ \Rightarrow BG=18-2 BG \\ \Rightarrow 3 BG =18 \\ \Rightarrow BG=\frac{18}{3} \\ \Rightarrow$ BG=6cm
इसी प्रकार से $\triangle ABC$ में CF भुजा AB की माध्यिका है।

$\frac{GC}{GF}=\frac{2}{1} \\ \Rightarrow \frac{GC}{4.5}=\frac{2}{1} \\ \Rightarrow$ GC=4.5×2=9cm
अतः CF=9+4.5
CF=13.5cm सेमी
उपर्युक्त उदाहरणों के द्वारा बिन्दुपथ और संगामी रेखाएं (Loci And Concurrent Lines) को समझ सकते हैं।

7.बिन्दुपथ और संगामी रेखाओं की समस्याएं (Loci And Concurrent Lines Problems)-

(1.)$\triangle ABC$ का लम्बकेन्द्र P है। सिद्ध कीजिए कि $\triangle PBC$ का लम्बकेन्द्र है।
(2.) $\triangle ABC$ में माध्यिकाएं AD, BE और CF बिन्दु G से गुजरती है।
(a)यदि GF=4 सेमी हो तो GC का मान ज्ञात कीजिए।
(b) यदि AD=7.5 cm हो तो GD का मान ज्ञात कीजिए।
(3.)एक त्रिभुज ABC की भुजाओं BC,CA और AB के मध्यबिन्दु क्रमशःD,E और F हों तो सिद्ध कीजिए कि EF,AD को समद्विभाजित करती है।
(4.)यदि एक त्रिभुज की सभी माध्यिकाएं समान हो तो वह समबाहु त्रिभुज होगा।
(5.)एक में,$\triangle ABC$ माध्यिकाएं AD, BE और CF एक बिन्दु G से गुजरती है।यदि AG=6cm,BE=12.6cm और FG=3 सेमी हो तो AD,GE और GC ज्ञात कीजिए।
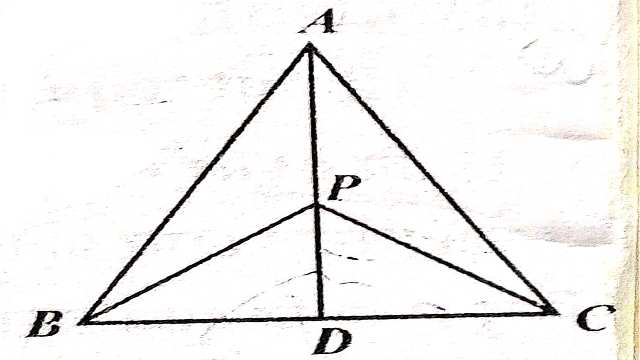
(6.)चित्र में बिन्दु P भुजा BC के लम्ब-समद्विभाजक AD पर हो तो सिद्ध कीजिए कि $\angle ABP=\angle ACP$

उत्तर (Answers):(2.)(a)GC=8cn,(b)GD=2.5cm
(5.)AD=9cm,GE=4.2cm,GC=6cm
उपर्युक्त सवालों को हल करने पर बिन्दुपथ और संगामी रेखाएं (Loci And Concurrent Lines) को ठीक से समझ सकते हैं।

8.लोकस लाइन क्या है? (What is locus line?)-

ज्यामिति में, एक बिन्दुपथ (बहुवचन: लोकी) ("स्थान" के लिए लैटिन शब्द,"स्थान") सभी बिंदुओं का एक सेट है (आमतौर पर, एक रेखा, एक रेखाखंड, एक वक्र या एक सतह), जिसका स्थान संतुष्ट है या एक या अधिक निर्दिष्ट शर्तों द्वारा निर्धारित किया जाता है।

9.यदि लाइनें संगामी हैं, तो इसका क्या मतलब है? (What does it mean if lines are concurrent?)-

यदि वे एक बिंदु पर प्रतिच्छेद करते हैं, तो समतल या उच्च-आयामी स्थान में रेखाएँ संगामी कहलाती हैं।
2-डी ज्यामिति में संगामी रेखाएं होती हैं, जो एक बिंदु पर एक-दूसरे को बिल्कुल काटती हैं। … इसलिए, हम कह सकते हैं कि सभी अप्रतिच्छेदी रेखाएं एक दूसरे के संगामी हैं।

10.मैथ्स में बिन्दुपथ क्या हैं? (What are loci in maths?)-

Loci समान गुणधर्मों वाले बिन्दुओं का एक समूह है। Loci का उपयोग लाइनों और आकृतियों के सटीक निर्माण के लिए किया जा सकता है।बियरिंग्स तीन आकृति कोण हैं जो उत्तर से दक्षिणावर्त मापा जाता है।

11.सभी बिंदुओं का बिन्दुपथ क्या है? (What is the locus of all points?)-

एक बिन्दुपथ सभी बिंदुओं का सेट है (आमतौर पर एक वक्र या सतह का निर्माण) कुछ शर्तो को संतुष्ट करता है। उदाहरण के लिए, दिए गए बिंदु से समदूऊ समतल में बिंदुओं का स्थान एक वृत्त है, और दिए गए बिंदु से त्रिविमीय निर्देशांक में समदूरस्थ बिंदुओं का समूह एक गोला है।
उपर्युक्त उदाहरणों, सवालों को हल करके तथा प्रश्नों के उत्तर द्वारा बिन्दुपथ और संगामी रेखाएं (Loci And Concurrent Lines) को भली-भांति समझ सकते हैं।

Also Read This Article:-Circumference and Area of the Circle

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Instagram	click here
4.	Linkedin	click here
5.	Facebook Page	click here