Lines and Angles Class 9
1.रेखाएँ और कोण कक्षा 9 (Lines and Angles Class 9),गणित में रेखाएँ और कोण (Lines and Angles in Mathematics):
रेखाएँ और कोण कक्षा 9 (Lines and Angles Class 9) के इस आर्टिकल में कोणों के विभिन्न प्रकार जो दो प्रतिच्छेदी रेखाओं तथा दो समान्तर रेखाओं पर एक प्रतिच्छेदी रेखा द्वारा बनाएं जाते हैं,का अध्ययन करेंगे।
कोण की परिभाषाएँ (Definitions of Angles):
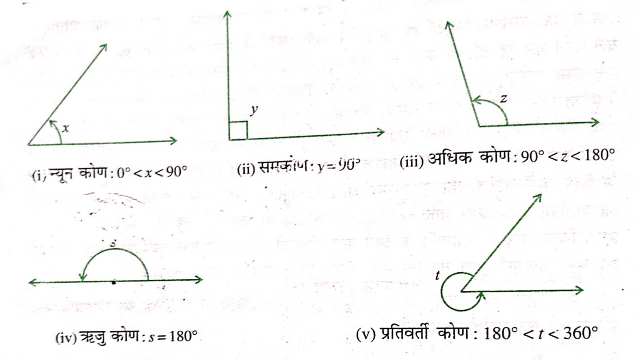
समकोण (Right Angle):एक समकोण का माप ठीक 90° होता है।
अधिक कोण (Obtuse Angle):90° से अधिक परन्तु 180° से कम वाला कोण अधिक कोण कहलाता है।
ऋजु कोण या सरल कोण (Straight Angle):ऋजु कोण 180° के बराबर होता है।
प्रतिवर्ती कोण (Reflex Angle):वह कोण जो 180° से अधिक परन्तु 360° से कम माप का होता है एक प्रतिवर्ती कोण कहलाता है।
पूरक कोण (Complementary Angles):यदि दो कोणों का योग एक समकोण के बराबर हो तो ऐसे कोण पूरक कोण कहलाते हैं।
संपूरक कोण (Supplementary Angles):वे दो कोण जिनका योग 180° हो सम्पूरक कोण कहलाते हैं।
आसन्न कोण (Adjacent Angles):दो कोण आसन्न कोण कहलाते हैं यदि उनमें एक उभयनिष्ठ शीर्ष हो,एक उभयनिष्ठ भुजा हो और उनकी वे भुजाएँ जो उभयनिष्ठ नहीं हैं,उभयनिष्ठ भुजा के विपरीत ओर स्थित हों।
कोणों का एक रैखिक युग्म (Linear Pair of Angles):अउभयनिष्ठ भुजाएँ BA और BC एक रेखा बनाएं तो इस स्थिति में \angle ABD और \angle DBC कोणों का एक रैखिक युग्म बनाते हैं।
शीर्षाभिमुख कोण (Vertically Opposite Angles):जो दो रेखाओं मान लीजिए AB और CD को परस्पर O बिन्दु पर प्रतिच्छेद से बनते हैं।यहाँ शीर्षाभिमुख कोणों के दो युग्म हैं।इनमें से एक युग्म \angle AOD और \angle BOC का है।
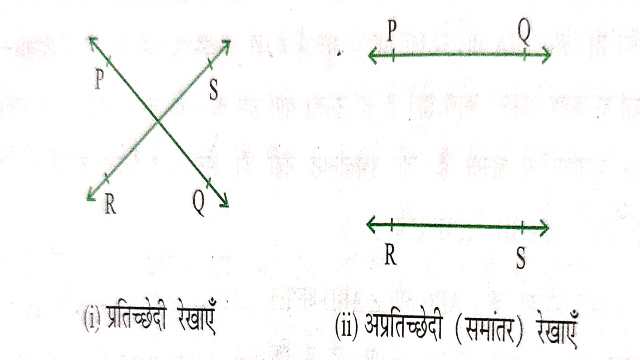
प्रतिच्छेदी रेखाएँ और अप्रतिच्छेदी रेखाएँ (Transversal Lines and Paralle Lines):रेखा की इस अवधारणा को भी याद कीजिए कि वह दोनों दिशाओं में अनिश्चित रूप से विस्तृत होती है।रेखाएँ PQ और RS आकृति (i) में प्रतिच्छेदी रेखाएँ हैं और आकृति (ii) में ये समान्तर रेखाएँ हैं।
इन दोनों समान्तर रेखाओं के विभिन्न बिन्दुओं पर उनके उभयनिष्ठ लम्बों की लम्बाईयाँ समान रहेंगी।यह लम्बाई दोनों समान्तर रेखाओं के बीच की दूरी कहलाती है।
अभिगृहीत 6.1:यदि एक किरण एक रेखा पर खड़ी हो तो इस प्रकार बने दोनों आसन्न कोणों का योग 180° होता है।
याद कीजिए कि जब दो आसन्न कोणों का योग 180° हो तो वे कोणों का एक रैखिक युग्म बनाते हैं।
अभिगृहीत में यह दिया गया है कि ‘एक किरण एक रेखा पर खड़ी हो’।इस दिए हुए से,हमने यह निष्कर्ष निकाला कि इस प्रकार बने दोनों कोणों का योग 180° होता है।इस अभिगृहीत का विलोम होगाः
(A) यदि दो आसन्न कोणों का योग 180° है तो एक किरण एक रेखा पर खड़ी होती है (अर्थात् अउभयनिष्ठ भुजाएँ एक ही रेखा में हैं)।
अभिगृहीत 6.1 और कथन (A) एक दूसरे के विपरीत हैं इनमें से प्रत्येक को एक दूसरे का विलोम (Converse) कहते हैं।
अभिगृहीत 6.2:यदि दो आसन्न कोणों का योग 180° है तो उनकी अउभयनिष्ठ भुजाएँ एक रेखा बनाती हैं।
स्पष्ट कारणों से उपर्युक्त दोनों अभिगृहीतों को मिलाकर रैखिक युग्म अभिगृहीत (Linear Pair Axiom) कहते हैं।
प्रमेय (Theorem):1.यदि दो रेखाएँ परस्पर प्रतिच्छेद करती हैं तो शीर्षाभिमुख कोण बराबर होते हैं।
उपपत्ति (Proof):उपर्युक्त कथन में यह दिया है कि दो रेखाएँ परस्पर प्रतिच्छेद करती हैं।अतः मान लीजिए कि AB और CD दो रेखाएँ हैं जो परस्पर बिन्दु O पर प्रतिच्छेद करती हैं।जैसा कि आकृति में दर्शाया गया है।इससे हमें शीर्षाभिमुख कोणों के निम्न दो युग्म प्राप्त होते हैं
(1.) \angle AOC और \angle BOD
(2.)\angle AOD और \angle BOC
हमें सिद्ध करना है किः \angle AOC=\angle BOD और \angle A O D=\angle B O C है।
अब किरण OA रेखा CD पर खड़ी है।
अतः \angle A O C+\angle A O D=180^{\circ} (रैखिक युग्म अभिगृहीत से)……(1)
इसी प्रकार \angle A O D+\angle B O D=180^{\circ} \cdots(2)
(1) और (2) से हम लिख सकते हैं कि
\angle A O C+\angle A O D=\angle A O D+\angle B O D \\ \Rightarrow \angle AOC=\angle BOD \\ \angle AOD=\angle BOC
इसी प्रकार सिद्ध किया जा सकता है कि है।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Versions to Euclid 5th Postulate
2.रेखाएँ और कोण कक्षा 9 के साधित उदाहरण (Lines and Angles Class 9 Solved Examples):
Example:1.आकृति में रेखाएँ AB और CD बिन्दु O पर प्रतिच्छेद करती हैं।यदि \angle AOC+\angle BOE=70^{\circ} है और \angle BOD=40^{\circ} है तो \angle BOE और प्रतिवर्ती \angle COE ज्ञात कीजिए।
Solution: \angle BOD=\angle AOC (शीर्षाभिमुख कोण)… (1)
\angle A O C=40^{\circ} \cdots \cdots \text { (2) } \\ \angle A O C+\angle B O E=70^{\circ} \cdots(3)
(2) व (3) सेः
40^{\circ}+\angle BOE=70^{\circ} \\ \Rightarrow \angle BOE=70^{\circ}-40^{\circ} \\ \Rightarrow \angle B O E=30^{\circ} \\ \angle AOC+\angle C O E+\angle BOE=180^{\circ} (रैखिक कोण युग्म से)
\Rightarrow 70^{\circ}+\angle C O E=180^{\circ} \text { [(3)से] } \\ \Rightarrow \angle COE= 180^{\circ}-70^{\circ} \\ \Rightarrow \angle COE=110^{\circ}
प्रतिवर्ती \angle C O E=360^{\circ}-110^{\circ}=250^{\circ} \\ \angle BOE=30^{\circ}
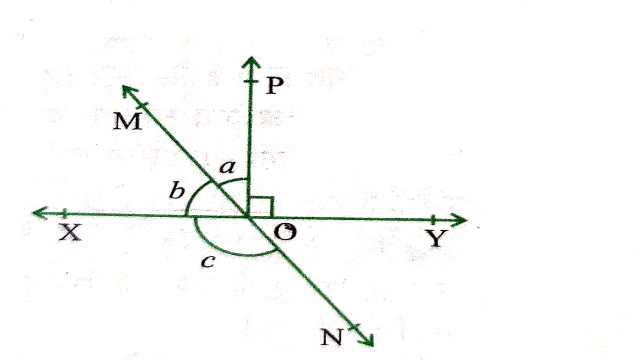
Example:2.आकृति में रेखाएँ XY और MN बिन्दु O पर प्रतिच्छेद करती हैं।यदि \angle POY=90^{\circ} और a:b=2:3 है तो c ज्ञात कीजिए।
Solution: a: b=2: 3 \\ 2 x+3 x=90^{\circ} \\ \Rightarrow 5 x=90^{\circ} \Rightarrow x=\frac{90}{5}=18^{\circ} \\ b=3 x=3 \times 18^{\circ}=54^{\circ} \\ \angle XON+\angle XOM=180^{\circ} (रैखिक युग्म अभिगृहीत से)
\Rightarrow c+b=180^{\circ} \\ \Rightarrow c+54^{\circ}=180^{\circ} \\ \Rightarrow c=180^{\circ}-54^{\circ} \\ \Rightarrow c=126^{\circ}
Example:3.आकृति में यदि \angle PQR=\angle PRQ है तो सिद्ध कीजिए कि \angle PQS=\angle PRT है।
Solution:दिया है (Given): \angle PQR=\angle PRQ
सिद्ध करना है (To Prove): \angle PQS=\angle PRT
उपपत्ति (Proof): \angle PQS+\angle PQR=180^{\circ} (रैखिक युग्म अभिगृहीत से)
\angle PRT+\angle PRQ=180^{\circ} (रैखिक युग्म अभिगृहीत से)……(2)
(1) व (2) सेः
\angle PQS+\angle PQR=\angle P R T+\angle P R Q \cdots(3) \\ \angle PQR=\angle PRQ \cdots(4)
(3) व (4) सेः
\angle PQS=\angle PRT
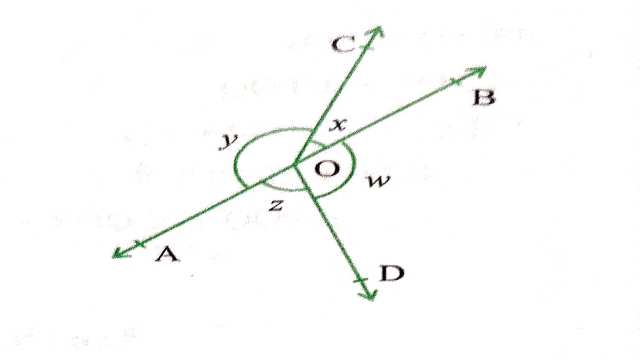
Example:4.आकृति में यदि x+y=w+z है तो सिद्ध कीजिए कि AOB एक रेखा है।
Solution:\angle AOC+\angle BOC+\angle A O D+\angle B O D=360^{\circ} (एक बिन्दु पर बने कोण)
\Rightarrow x+y+w+z=360^{\circ} \cdots(1) \\ x+y=w+z (दिया है)…..(2)
\Rightarrow x+y+x+y=360^{\circ} \\ \Rightarrow 2 x+2 y=360^{\circ} \\ \Rightarrow 2(x+y)=360^{\circ} \\ \Rightarrow x+y=\frac{360}{2} \\ \Rightarrow x+y=180^{\circ}
अतः रैखिक युग्म अभिगृहीत के विलोम से AOB एक सरल रेखा है।
Example:5.आकृति में POQ एक रेखा है।किरण OR रेखा PQ पर लम्ब है।किरणों OP और OR के बीच में OS एक अन्य किरण है।सिद्ध कीजिएः \angle ROS=\frac{1}{2}(\angle QOS-\angle POS)
Solution:दिया है (Given): PQ \perp O R
सिद्ध करना है (To Prove): \angle R O S=\frac{1}{2}(\angle Q O S-\angle P O S)
उपपत्ति (Proof): \angle P O S=\angle Q O R=90^{\circ}(P Q \perp O R) \\ \Rightarrow \angle POS+\angle ROS=\angle QOR \cdots(1) \\ \angle QOS=\angle QOR+\angle ROS \\ \Rightarrow \angle QOR=\angle QOS-\angle ROS \cdots(2)
(1) व (2) सेः
\angle POS+\angle ROS=\angle QOS-\angle ROS \\ \Rightarrow \angle ROS+\angle ROS=\angle QOS-\angle PQS \\ \Rightarrow 2 \angle ROS=\angle QOS-\angle POS \\ \Rightarrow \angle ROS=\frac{1}{2}(\angle QOS-\angle POS)
Example:6.यह दिया गया है कि है \angle XYZ=64^{\circ} और XY को बिन्दु P तक बढ़ाया गया है।दी गई सूचना से एक आकृति खींचिए।यदि किरण YQ, \angle ZYP को समद्विभाजित करती है तो \angle XYQ और प्रतिवर्ती \angle QYP के मान ज्ञात कीजिए।
Solution:\angle XYZ=64^{\circ}(दिया है)
\angle XYZ+\angle ZYP=180^{\circ} (रैखिक युग्म अभिगृहीत से)
64^{\circ}+\angle ZY P=180^{\circ} \\ \Rightarrow \angle ZYP=180^{\circ}-64^{\circ} \\ \Rightarrow \angle ZYP=116^{\circ}
परन्तु \angle ZYP का अर्धक YQ है।
\therefore \angle ZYQ=\angle Q Y P=\frac{116^{\circ}}{2}=58^{\circ} \\ \therefore \angle XYQ= \angle X Y Z+\angle ZYQ \\=64^{\circ}+58^{\circ} \\ \Rightarrow \angle X Y Q=122^{\circ}
अब प्रतिवर्ती \angle Q Y P=360^{\circ}-\angle QYP \\ =360^{\circ}-58^{\circ}
प्रतिवर्ती \angle QYP=302^{\circ}
तथा \angle XYQ=122^{\circ}
उपर्युक्त उदाहरणों के द्वारा रेखाएँ और कोण कक्षा 9 (Lines and Angles Class 9),गणित में रेखाएँ और कोण (Lines and Angles in Mathematics) को समझ सकते हैं।
3.रेखाएँ और कोण कक्षा 9 पर आधारित सवाल (Questions Based on Lines and Angles Class 9):
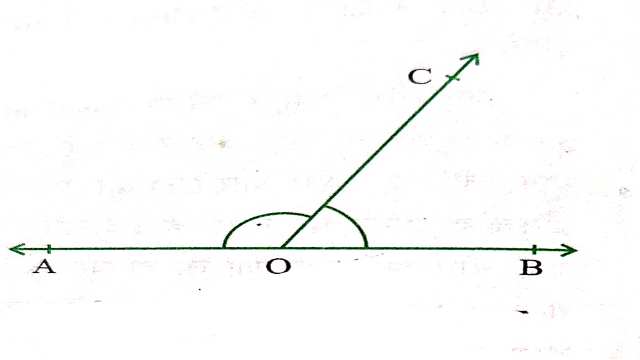
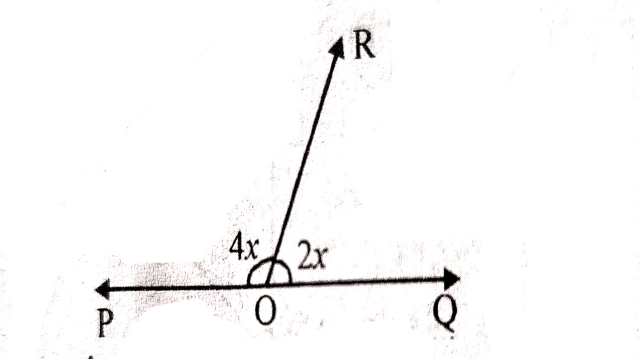
(1.)आकृति में POQ एक सरल रेखा है, \angle POR=4x और \angle QOR=2 x तो x का मान ज्ञात करो।
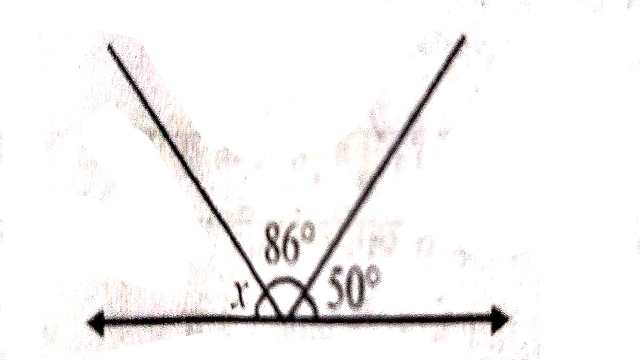
(2.)दी गई आकृति से \angle x का मान ज्ञात कीजिए।
उपर्युक्त सवालों को हल करने पर रेखाएँ और कोण कक्षा 9 (Lines and Angles Class 9),गणित में रेखाएँ और कोण (Lines and Angles in Mathematics) को ठीक से समझ सकते हैं।
Also Read This Article:-Euclid Geometry Class 9
4.रेखाएँ और कोण कक्षा 9 (Frequently Asked Questions Related to Lines and Angles Class 9),गणित में रेखाएँ और कोण (Lines and Angles in Mathematics) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्नः
प्रश्नः1.संरेख और असंरेख बिन्दु किसे कहते हैं? (What is Collinear and Non-Collinear Points?):
उत्तरःयदि तीन या अधिक बिन्दु एक ही रेखा पर स्थित हों तो वे संरेख बिन्दु (Collinear Points) कहलाते हैं अन्यथा वे असंरेख बिन्दु (Non-Collinear) कहलाते हैं।
प्रश्नः2.कोण की भुजाएँ और कोण का शीर्ष किसे कहते हैं? (What is Sides of Angle and Vertex of Angle Called?):
उत्तरःजब दो किरणें एक ही अंत बिन्दु से प्रारम्भ होती हैं तो एक कोण (angle) बनता है।कोण को बनाने वाली दोनों किरणें कोण की भुजाएँ (arms या sides) कहलाती हैं और वह उभयनिष्ठ अंत बिन्दु कोण का शीर्ष (Vertex) कहलाता है।
प्रश्न:3.न्यून कोण किसे कहते हैं? (What is Acute Angle?):
उत्तरःन्यून कोण (Acute Angle):वह कोण जिसका माप 0° से अधिक एवं 90° से कम हो अर्थात् 0° और 90° के बीच का कोण न्यून कोण कहलाता है।
उपर्युक्त प्रश्नों के उत्तर द्वारा रेखाएँ और कोण कक्षा 9 (Lines and Angles Class 9),गणित में रेखाएँ और कोण (Lines and Angles in Mathematics) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Lines and Angles Class 9
रेखाएँ और कोण कक्षा 9 (Lines and Angles Class 9)
Lines and Angles Class 9
रेखाएँ और कोण कक्षा 9 (Lines and Angles Class 9) के इस आर्टिकल में कोणों के विभिन्न प्रकार
जो दो प्रतिच्छेदी रेखाओं तथा दो समान्तर रेखाओं पर एक प्रतिच्छेदी रेखा द्वारा बनाएं जाते हैं
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.