Linear Inequality in Two Variables
1.दो चर राशियों की रैखिक असमिकाएँ (Linear Inequality in Two Variables),दो चर राशियों की रैखिक असमिका निकाय का हल कक्षा 11 (Solution of System of Linear Inequalities in Two Variables Class 11):
दो चर राशियों की रैखिक असमिकाएँ (Linear Inequality in Two Variables) के इस आर्टिकल में दो चर राशियों की असमिका निकाय पर आधारित सवालों को लेखाचित्र विधि से हल ज्ञात करना सीखेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Linear Inequalities Class 11
2.दो चर राशियों की रैखिक असमिकाओं के उदाहरण (Linear Inequality in Two Variables in Two Variables Illustrations):
प्रश्न 1 से 15 तक निम्नलिखित असमिका निकाय को आलेखीय विधि से हल कीजिए:
(graphically):
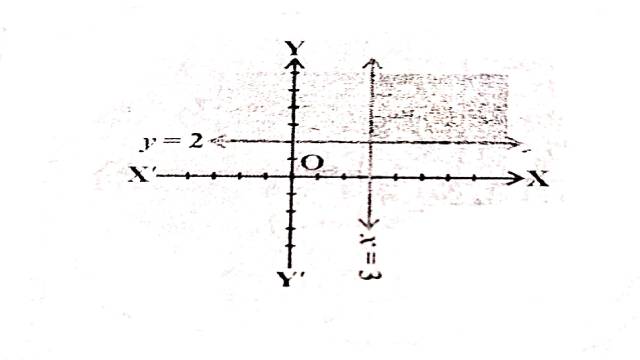
Illustration:1. x \geq 3, y \geq 2
Solution: x \geq 3, y \geq 2
दी गई असमिकाओं के संगत समीकरण हैं:
x=3,y=2
x=3 मूलबिन्दु से दायीं ओर 3 इकाई दूरी पर y-अक्ष के समान्तर एक रेखा है।मूलबिन्दु असमिका x \geq 3, 0 \geq 3 को सन्तुष्ट नहीं करता है अतः मूलबिन्दु हल क्षेत्र में समाविष्ट नहीं है।अतः हल क्षेत्र रेखा x=3 पर स्थित बिन्दुओं सहित दायीं ओर है।
y=2 मूलबिन्दु से ऊपर की ओर 2 इकाई दूरी पर x-अक्ष के समान्तर एक रेखा है।मूलबिन्दु असमिका y \geq 2 \Rightarrow 0 \geq 2 को सन्तुष्ट नहीं करता है अतः मूलबिन्दु हल क्षेत्र में समाविष्ट नहीं है। अतः हल क्षेत्र रेखा y=2 पर स्थित बिन्दुओं सहित ऊपर की ओर है।
अतः दी गई असमिकाओं का उभयनिष्ठ हल क्षेत्र चित्र में छायांकित भाग द्वारा दर्शाया गया है।
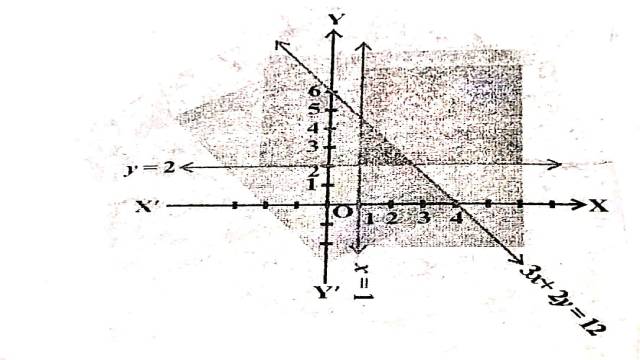
Illustration:2. 3 x+2 y \leq 12, x \geq 1, y \geq 2
Solution: 3 x+2 y \leq 12, x \geq 1, y \geq 2
दी गई असमिकाओं के संगत समीकरण हैं:
3x+2y=12,x=1,y=2
3x+2y=12 अक्षों को (4,0) तथा (0,6) पर मिलती हैं।बिन्दुओं को गहरी रेखा द्वारा मिलाते हैं।मूलबिन्दु असमिका 3 x+2 y \leq 12 \Rightarrow 3(0)+2(0) \leq 12 \Rightarrow 0 \leq 12 को सन्तुष्ट करता है।इसलिए रेखा पर स्थित बिन्दुओं सहित मूलबिन्दु हल क्षेत्र में समाविष्ट है।
x=1 मूलबिन्दु से दायीं ओर 1 इकाई दूरी पर y-अक्ष के समान्तर एक रेखा है।मूलबिन्दु असमिका x \geq 1 \Rightarrow 0 \geq 1 को सन्तुष्ट नहीं करता है अतः मूलबिन्दु हल क्षेत्र में समाविष्ट नहीं है।अतः हल क्षेत्र रेखा x=1 पर स्थित बिन्दुओं सहित दायीं ओर है।
y=2 मूलबिन्दु से ऊपर की ओर 2 इकाई दूरी पर x-अक्ष के समान्तर एक रेखा है।मूलबिन्दु असमिका y \geq 2 \Rightarrow 0 \geq 2 को सन्तुष्ट नहीं करता है अतः मूलबिन्दु हल क्षेत्र में समाविष्ट नहीं है।अतः हल क्षेत्र रेखा y=2 पर स्थित बिन्दुओं सहित ऊपर की ओर है।
अतः दी गई असमिकाओं का उभयनिष्ठ हल क्षेत्र चित्र में छायांकित भाग द्वारा दर्शाया गया है।
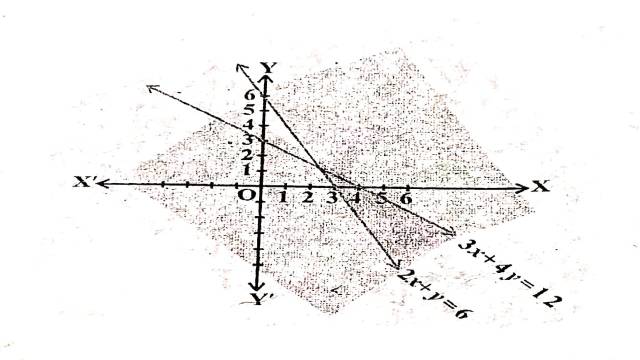
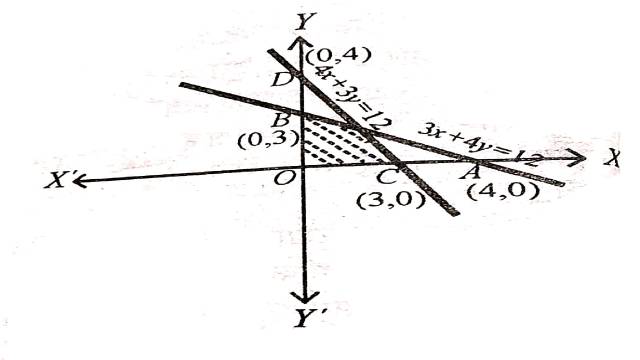
Illustration:3. 2 x+y \geq 6,3 x+4 y \leq 12
Solution: 2 x+y \geq 6,3 x+4 y \leq 12
दी गई असमिकाओं के संगत समीकरण हैं:
2x+y=6,3x+4y=12
2x+y=6 अक्षों को (3,0) तथा (0,6) पर मिलती है।बिन्दुओं को गहरी रेखा द्वारा मिलाते हैं।मूलबिन्दु असमिका 2 x+y \geq 6 \Rightarrow 2(0)+0 \geq 6 \Rightarrow 0 \geq 6 को सन्तुष्ट नहीं करता है।इसलिए मूलबिन्दु हल क्षेत्र में समाविष्ट नहीं है।अतः हल क्षेत्र रेखा 2x+y=6 पर स्थित बिन्दुओं सहित मूलबिन्दु से विपरीत ओर स्थित है।
3x+4y=12 अक्षों को (4,0) तथा (0,3) पर मिलती है।बिन्दुओं को गहरी रेखा द्वारा मिलाते हैं।मूलबिन्दु असमिका 3 x+4 y \leq 12 \Rightarrow 3(0)+4(0) \leq 12 \Rightarrow 0 \leq 12 को सन्तुष्ट करता है।इसलिए रेखा पर स्थित बिन्दुओं सहित मूलबिन्दु हल क्षेत्र में समाविष्ट है।
अतः दी गई असमिकाओं का उभयनिष्ठ हल क्षेत्र चित्र में छायांकित भाग द्वारा दर्शाया गया है।
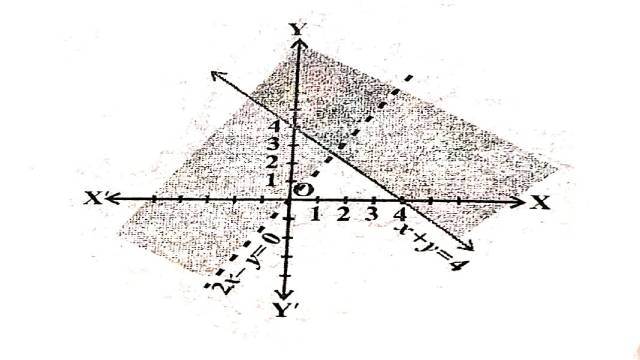
Illustration:4. x+y \geq 4,2 x-y>0
Solution: x+y \geq 4,2 x-y>0
दी गई असमिकाओं के संगत समीकरण हैं:
x+y=4,2x-y=0
x+y=4 अक्षों को (4,0) तथा (0,4) पर मिलती है।बिन्दुओं को गहरी रेखा द्वारा मिलाते हैं।मूलबिन्दु असमिका x+y \geq 6 \Rightarrow 0+0 \geq 6 \Rightarrow 0 \geq 6 को सन्तुष्ट नहीं करता है।इसलिए मूलबिन्दु हल क्षेत्र में समाविष्ट नहीं है।अतः हल क्षेत्र रेखा x+y=4 पर स्थित बिन्दुओं सहित मूलबिन्दु से विपरीत ओर स्थित है।
2x-y=0 मूलबिन्दु,प्रथम पाद व तृतीय पाद से होकर गुजरती है।मूलबिन्दु असमिका 2 x-y>0 \Rightarrow 2(0)-0>0 \Rightarrow 0>0 को सन्तुष्ट नहीं करता है।इसलिए हल क्षेत्र मूलबिन्दु से रेखा के ऊपर की ओर स्थित है।
अतः दी गई असमिकाओं का उभयनिष्ठ हल क्षेत्र चित्र में छायांकित भाग द्वारा दर्शाया गया है।
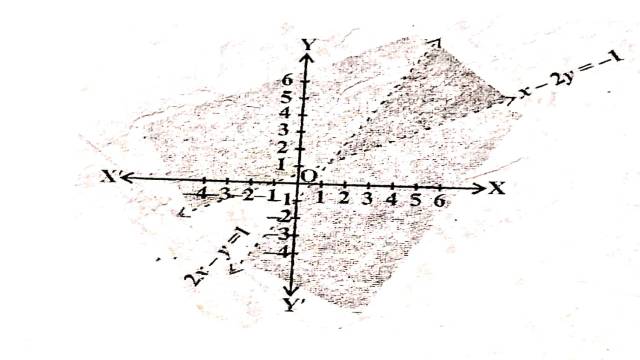
Illustration:5.2x-y>1,x-2y<-1
Solution: 2x-y>1,x-2y<-1
दी गई असमिकाओं के संगत समीकरण हैं:
2x-y=1,x-2y=-1
2x-y=1 अक्षों को \left(\frac{1}{2}, 0\right) तथा (0,-1) पर मिलती है।बिन्दुओं को खण्डित रेखा द्वारा मिलाते हैं।मूलबिन्दु असमिका 2 x-y>1 \Rightarrow 2(0)-0>1 \Rightarrow 0>1 को सन्तुष्ट नहीं करता है।इसलिए मूलबिन्दु हल क्षेत्र में समाविष्ट नहीं है।अतः हल क्षेत्र रेखा 2x-y=1 से मूलबिन्दु के विपरीत ओर स्थित है। x-2y=-1 अक्षों को (-1,0) तथा \left(0, \frac{1}{2}\right) पर मिलती है।बिन्दुओं को खण्डित रेखा द्वारा मिलाते हैं।मूलबिन्दु असमिका x-2y <-1 \Rightarrow 0-2(0)<-1 \Rightarrow 0<-1 को सन्तुष्ट नहीं करता है।इसलिए मूलबिन्दु हल क्षेत्र में समाविष्ट नहीं है।अतः हल क्षेत्र रेखा x-2y=-1 से मूलबिन्दु के विपरीत ओर स्थित है।
अतः दी गई असमिकाओं का उभयनिष्ठ हल क्षेत्र चित्र में छायांकित भाग द्वारा दर्शाया गया है।
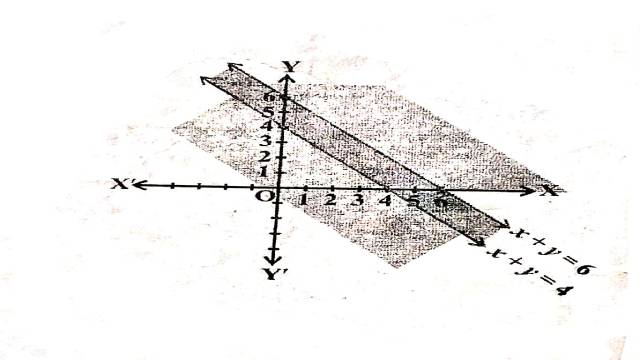
Illustration:6. x+y \leq 6, x+y \geq 4
Solution: x+y \leq 6, x+y \geq 4
दी गई असमिकाओं के संगत समीकरण हैं:
x+y=6,x+y=4
x+y=6 अक्षों को (6,0) तथा (0,6) पर मिलती हैं।बिन्दुओं को गहरी रेखा द्वारा मिलाते हैं।मूलबिन्दु असमिका x+y \leq 6 \Rightarrow 0+0 \leq 6 \Rightarrow 0 \leq 6 को सन्तुष्ट करता है।इसलिए रेखा पर स्थित बिन्दुओं सहित मूलबिन्दु हल क्षेत्र में समाविष्ट है। x+y=4 अक्षों को (4,0) तथा (0,4) पर मिलती है।बिन्दुओं को गहरी रेखा द्वारा मिलाते हैं।मूलबिन्दु असमिका x+y \geq 4 \Rightarrow 0+0 \geq 4 \Rightarrow 0 \geq 4 को सन्तुष्ट नहीं करता है।इसलिए मूलबिन्दु हल क्षेत्र में समाविष्ट नहीं है।अतः हल क्षेत्र रेखा x+y=4 पर स्थित बिन्दुओं सहित मूलबिन्दु से विपरीत ओर स्थित है।
अतः दी गई असमिकाओं का उभयनिष्ठ हल क्षेत्र चित्र में छायांकित भाग द्वारा दर्शाया गया है।
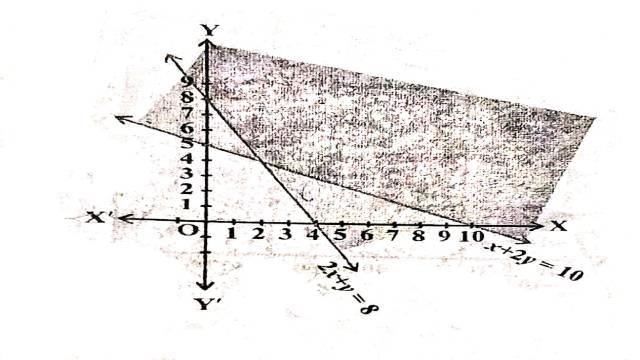
Illustration:7. 2 x+y \geq 8, x+2 y \geq 10
Solution: 2 x+y \geq 8, x+2 y \geq 10
दी गई असमिकाओं के संगत समीकरण हैं:
2x+y=8,x+2y=10
2x+y=8 अक्षों को (4,0) तथा (0,8) पर मिलती है।बिन्दुओं को गहरी रेखा द्वारा मिलाते हैं।मूलबिन्दु असमिका 2 x+y \geq 8 \Rightarrow 2(0)+0 \geq 8 \Rightarrow 0 \geq 8 को सन्तुष्ट नहीं करता है।इसलिए मूलबिन्दु हल क्षेत्र में समाविष्ट नहीं है।अतः हल क्षेत्र रेखा 2x+y=8 पर स्थित बिन्दुओं सहित मूलबिन्दु से विपरीत ओर स्थित है। x+2y=10 अक्षों को (10,0) तथा (0,5) पर मिलती है।बिन्दुओं को गहरी रेखा द्वारा मिलाते हैं।मूलबिन्दु असमिका x+2 y \geq 10 \Rightarrow 0+2(0) \geq 10 \Rightarrow 0 \geq 10 को सन्तुष्ट नहीं करता है।इसलिए मूलबिन्दु हल क्षेत्र में समाविष्ट नहीं है।अतः हल क्षेत्र रेखा x+2y=10 पर स्थित बिन्दुओं सहित मूलबिन्दु से विपरीत ओर स्थित है। अतः दी गई असमिकाओं का उभयनिष्ठ हल क्षेत्र चित्र में छायांकित भाग द्वारा दर्शाया गया है।
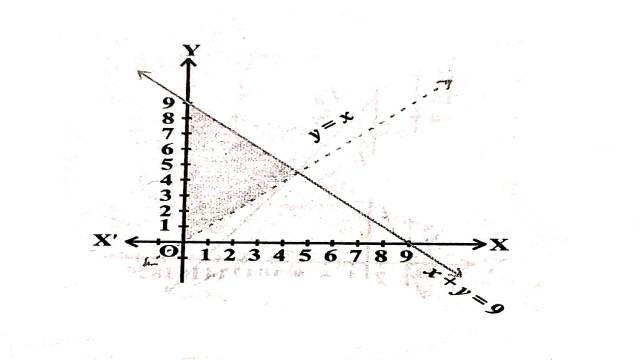
Illustration:8. x+y \leq 9, y>x, x \geq 0
Solution: x+y \leq 9, y>x, x \geq 0
दी गई असमिकाओं के संगत समीकरण हैं:
x+y=9,y=x,x=0
x+y=9 अक्षों को (9,0) तथा (0,9) पर मिलती हैं।बिन्दुओं को गहरी रेखा द्वारा मिलाते हैं।मूलबिन्दु असमिका x+y \leq 9 \Rightarrow 0+0 \leq 9 \Rightarrow 0 \leq 9 को सन्तुष्ट करता है।इसलिए रेखा पर स्थित बिन्दुओं सहित मूलबिन्दु हल क्षेत्र में समाविष्ट है। y=x मूलबिन्दु,प्रथम पाद व तृतीय पाद से होकर गुजरती है।मूलबिन्दु असमिका y>x \Rightarrow 0>0 को सन्तुष्ट नहीं करता है।इसलिए हल क्षेत्र मूलबिन्दु से रेखा के ऊपर की ओर स्थित है।
x=0 प्रथम पाद को प्रदर्शित करता है।
अतः दी गई असमिकाओं का उभयनिष्ठ हल क्षेत्र चित्र में छायांकित भाग द्वारा दर्शाया गया है।
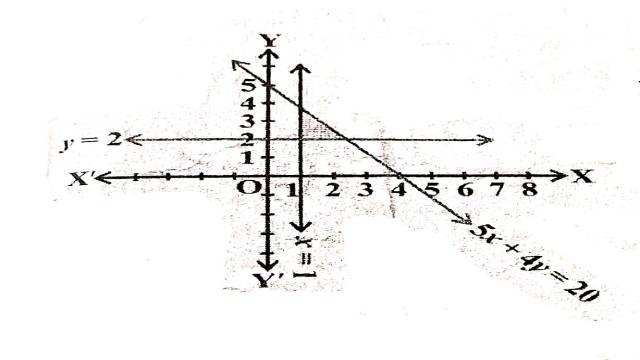
Illustration:9. 5 x+4 y \leq 20, x \geq 1, y \geq 2
Solution: 5 x+4 y \leq 20, x \geq 1, y \geq 2
दी गई असमिकाओं के संगत समीकरण हैं:
5x+4y=20,x=1,y=2
5x+4y=20 अक्षों को (4,0) तथा (0,5) पर मिलती हैं।बिन्दुओं को गहरी रेखा द्वारा मिलाते हैं।मूलबिन्दु असमिका 5 x+4 y \leq 20 \Rightarrow 5(0)+4(0) \leq 20 \Rightarrow 0 \leq 20 को सन्तुष्ट करता है।इसलिए रेखा पर स्थित बिन्दुओं सहित मूलबिन्दु हल क्षेत्र में समाविष्ट है।
x=1 यह मूलबिन्दु से दायीं ओर 1 इकाई दूरी पर y-अक्ष के समान्तर एक रेखा है।मूलबिन्दु असमिका x \geq 1 \Rightarrow 0 \geq 1 को सन्तुष्ट नहीं करता है।इसलिए मूलबिन्दु हल क्षेत्र में समाविष्ट नहीं है।अतः हल क्षेत्र रेखा x=1 पर स्थित बिन्दुओं सहित मूलबिन्दु दायीं ओर स्थित है।
y=2 यह मूलबिन्दु से ऊपर 2 इकाई दूरी पर x-अक्ष के समान्तर एक रेखा है।असमिका y \geq 2 \Rightarrow 0 \geq 2 को मूलबिन्दु सन्तुष्ट नहीं करता है इसलिए मूलबिन्दु हल क्षेत्र में समाविष्ट नहीं है।अतः हल क्षेत्र रेखा y=2 पर स्थित बिन्दुओं सहित मूलबिन्दु के विपरीत ओर स्थित है।
अतः दी गई असमिकाओं का उभयनिष्ठ हल क्षेत्र चित्र में छायांकित भाग द्वारा दर्शाया गया है।
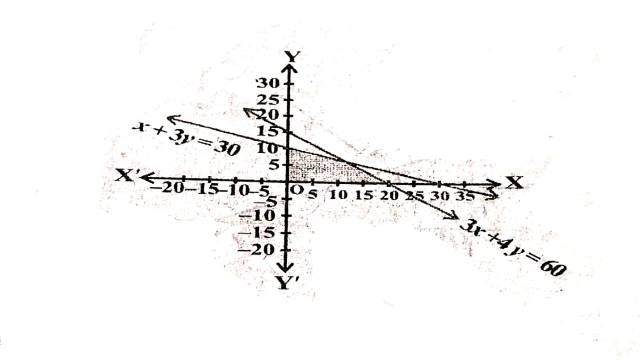
Illustration:10. 3 x+4 y \leq 60, x+3 y \leq 30,x \geq, y \geq 0
Solution: 3 x+4 y \leq 60, x+3 y \leq 30,x \geq, y \geq 0
दी गई असमिकाओं के संगत समीकरण हैं:
3x+4y=60,x+3y=30,x=0,y=0
3x+4y=20 अक्षों को \left(\frac{20}{3}, 0\right) तथा (0,5) पर मिलती हैं।बिन्दुओं को गहरी रेखा द्वारा मिलाते हैं।मूलबिन्दु असमिका 3 x+4 y \leq 60 \Rightarrow 3(0)+4(0) \leq 60 \Rightarrow 0 \leq 60 को सन्तुष्ट करता है।इसलिए रेखा पर स्थित बिन्दुओं सहित मूलबिन्दु हल क्षेत्र में समाविष्ट है।
x+3y=30 अक्षों को (30,0) तथा (0,10) पर मिलती हैं।बिन्दुओं को गहरी रेखा द्वारा मिलाते हैं।मूलबिन्दु असमिका x+34 \leq 30 \Rightarrow 0+3(0) \leq 30 \Rightarrow 0 \leq 30 को सन्तुष्ट करता है।इसलिए रेखा पर स्थित बिन्दुओं सहित मूलबिन्दु हल क्षेत्र में समाविष्ट है।
स्पष्टतः x \geq 0 तथा y \geq 0 प्रथम पाद को प्रदर्शित करते हैं।
अतः दी गई असमिकाओं का उभयनिष्ठ हल क्षेत्र चित्र में छायांकित भाग द्वारा दर्शाया गया है।
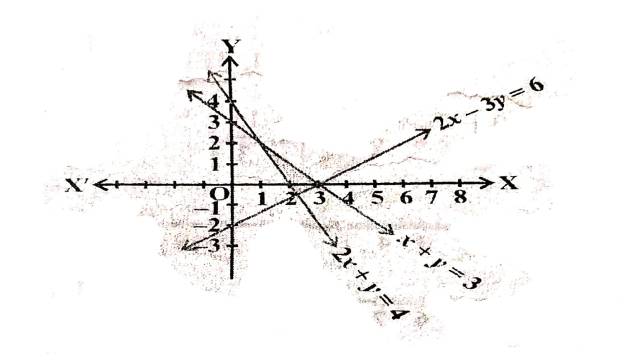
Illustration:11. 2 x+y \geq 4, x+y \leq 3,2 x-3 y \leq 6
Solution: 2 x+y \geq 4, x+y \leq 3,2 x-3 y \leq 6
दी गई असमिकाओं के संगत समीकरण हैं:
2x+y=4,x+y=3,2x-3y=6
2x+y=4 अक्षों को (2,0) तथा (0,4) पर मिलती है।बिन्दुओं को गहरी रेखा द्वारा मिलाते हैं।मूलबिन्दु असमिका 2 x+y=4 \Rightarrow 2(0)+0 \geq 4 \Rightarrow 0 \geq 4 को सन्तुष्ट नहीं करता है।इसलिए मूलबिन्दु हल क्षेत्र में समाविष्ट नहीं है।अतः हल क्षेत्र रेखा 2x+y=4 पर स्थित बिन्दुओं सहित मूलबिन्दु से विपरीत ओर स्थित है।
x+y=3 अक्षों को (3,0) तथा (0,3) पर मिलती है।बिन्दुओं को गहरी रेखा द्वारा मिलाते हैं।मूलबिन्दु असमिका x+y \leq 3 \Rightarrow 0+0 \leq 3 \Rightarrow 0 \leq 3 को सन्तुष्ट करता है।इसलिए रेखा पर स्थित बिन्दुओं सहित मूलबिन्दु हल क्षेत्र में समाविष्ट है।
2x-3y=6 अक्षों को (3,0) तथा (0,-2) पर मिलती है।बिन्दुओं को गहरी रेखा द्वारा मिलाते हैं।मूलबिन्दु असमिका 2x-3 y \leq 6 \Rightarrow 2(0)-3(0) \leq 6 \Rightarrow 0 \leq 6 को सन्तुष्ट करता है।इसलिए रेखा पर स्थित बिन्दुओं सहित मूलबिन्दु हल क्षेत्र में समाविष्ट है।
अतः दी गई असमिकाओं का उभयनिष्ठ हल क्षेत्र चित्र में छायांकित भाग द्वारा दर्शाया गया है।
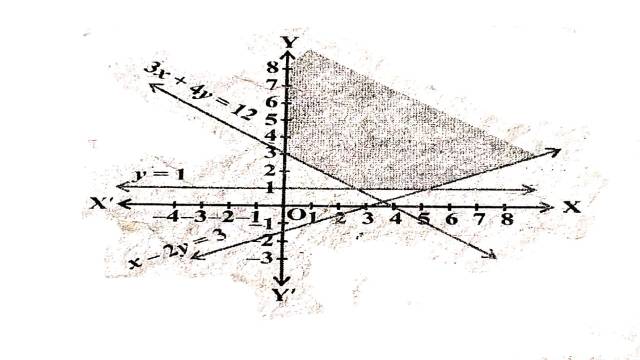
Illustration:12. x-2 y \leq 3,3 x+4 y \geq 12, x \geq 0, y \geq 1
Solution: x-2 y \leq 3,3 x+4 y \geq 12, x \geq 0, y \geq 1
दी गई असमिकाओं के संगत समीकरण हैं:
x-2y=3,3x+4y=12,x=0,y=1
x-2y=3 अक्षों को (3,0) तथा \left(0,-\frac{3}{2}\right) पर मिलती है।बिन्दुओं को गहरी रेखा द्वारा मिलाते हैं।मूलबिन्दु असमिका x-2 y \leq 3 \Rightarrow 0-2(0) \leq 3 \Rightarrow 0 \leq 3 को सन्तुष्ट करता है।इसलिए रेखा पर स्थित बिन्दुओं सहित मूलबिन्दु हल क्षेत्र में समाविष्ट है।
3x+4y=12 अक्षों को (4,0) तथा (0,3) पर मिलती है।बिन्दुओं को गहरी रेखा द्वारा मिलाते हैं।मूलबिन्दु असमिका 3 x+4 y \geq 12 \Rightarrow 3(0)+4(0) \leq 12 \Rightarrow 0 \geq 12को सन्तुष्ट नहीं करता है।इसलिए मूलबिन्दु हल क्षेत्र में समाविष्ट नहीं है।अतः हल क्षेत्र रेखा 3x+4y=12 पर स्थित बिन्दुओं सहित मूलबिन्दु से विपरीत ओर स्थित है।
स्पष्टतः x \geq 0 प्रथम पाद को प्रदर्शित करता है।
y=1 यह मूलबिन्दु से ऊपर 1 इकाई दूरी पर x-अक्ष के समान्तर एक रेखा है।असमिका को मूलबिन्दु y \geq 1 \Rightarrow 0 \geq 1 सन्तुष्ट नहीं करता है इसलिए मूलबिन्दु हल क्षेत्र में समाविष्ट नहीं है।अतः हल क्षेत्र रेखा y=1 पर स्थित बिन्दुओं सहित मूलबिन्दु के विपरित ओर स्थित है।
अतः दी गई असमिकाओं का उभयनिष्ठ हल क्षेत्र चित्र में छायांकित भाग द्वारा दर्शाया गया है।
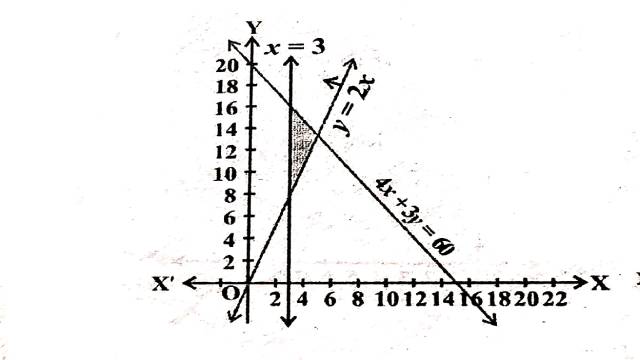
Illustration:13. 4 x+3 y \leq 60, y \geq 2 x, x \geq 3, x, y \geq 0
Solution: 4 x+3 y \leq 60, y \geq 2 x, x \geq 3, x, y \geq 0
दी गई असमिकाओं के संगत समीकरण हैं:
4x+3y=60,y=2x,x=3,x=0,y=0
4x+3y=60 अक्षों को (15,0) तथा (0,20) पर मिलती है।बिन्दुओं को गहरी रेखा द्वारा मिलाते हैं।मूलबिन्दु असमिका 4 x+3 y \leq 60 \Rightarrow 4(0)+3(0) \leq 60 \Rightarrow 0 \leq 60 को सन्तुष्ट करता है।इसलिए रेखा पर स्थित बिन्दुओं सहित मूलबिन्दु हल क्षेत्र में समाविष्ट है।
y=2x स्पष्टतः मूलबिन्दु,प्रथमपाद व तृतीय पाद से गुजरती है।मूलबिन्दु असमिका y \geq 2 x \Rightarrow 0 \geq 0 को सन्तुष्ट करती है इसलिए हल क्षेत्र रेखा के ऊपर की ओर स्थित है।
x=3 यह मूलबिन्दु से दायीं ओर 3 इकाई दूरी पर y-अक्ष के समान्तर एक रेखा है।असमिका x \geq 3 \Rightarrow 0 \geq 3 को मूलबिन्दु सन्तुष्ट नहीं करता है इसलिए मूलबिन्दु हल क्षेत्र में समाविष्ट नहीं है।अतः हल क्षेत्र रेखा x=3 पर स्थित बिन्दुओं सहित मूलबिन्दु से विपरीत ओर स्थित है।
स्पष्टतः x \geq 0 तथा y \geq 0 प्रथम पाद को प्रदर्शित करते हैं।
अतः दी गई असमिकाओं का उभयनिष्ठ हल क्षेत्र चित्र में छायांकित भाग द्वारा दर्शाया गया है।
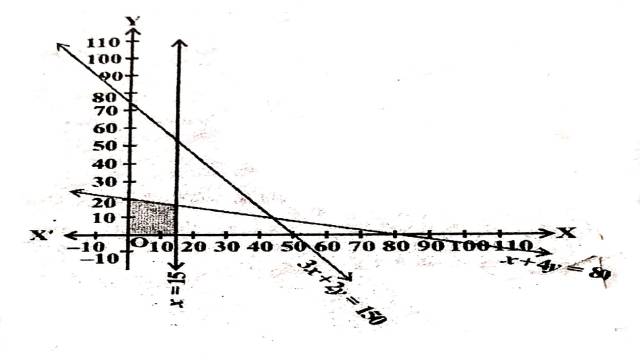
Illustration:14. 3 x+2 y \leq 150, x+4 y \leq 80, x \leq 15, y \geq 0,x \geq 0
Solution: 3 x+2 y \leq 150, x+4 y \leq 80, x \leq 15, y \geq 0,x \geq 0
दी गई असमिकाओं के संगत समीकरण हैं:
3x+2y=150,x+4y=80,x=15,y=0,x=0
3x+2y=150 अक्षों को (50,0) तथा \left(0, \frac{75}{2}\right) पर मिलती है।बिन्दुओं को गहरी रेखा द्वारा मिलाते हैं।मूलबिन्दु असमिका 3 x+2 y \leq 150 \Rightarrow 3(0)+2(0) \leq 150 \Rightarrow 0 \leq 150 को सन्तुष्ट करता है।इसलिए रेखा पर स्थित बिन्दुओं सहित मूलबिन्दु हल क्षेत्र में समाविष्ट है।
x+4y=80 अक्षों को (80,0) तथा (0,20) पर मिलती है।बिन्दुओं को गहरी रेखा द्वारा मिलाते हैं।मूलबिन्दु असमिका x+4 y \leq 80 \\ \Rightarrow 0+4(0) \leq 80 \Rightarrow 0 \leq 80 को सन्तुष्ट करता है।इसलिए रेखा पर स्थित बिन्दुओं सहित मूलबिन्दु हल क्षेत्र में समाविष्ट है।
x=15 यह मूलबिन्दु से दायीं ओर 15 इकाई दूरी पर y-अक्ष के समान्तर एक रेखा है।असमिका को मूलबिन्दु x \leq 15 \Rightarrow 0 \leq 15 सन्तुष्ट करता है इसलिए मूलबिन्दु हल क्षेत्र में समाविष्ट है।
स्पष्टतः x \geq 0 तथा y \geq 0 प्रथम पाद को प्रदर्शित करते हैं।
अतः दी गई असमिकाओं का उभयनिष्ठ हल क्षेत्र चित्र में छायांकित भाग द्वारा दर्शाया गया है।
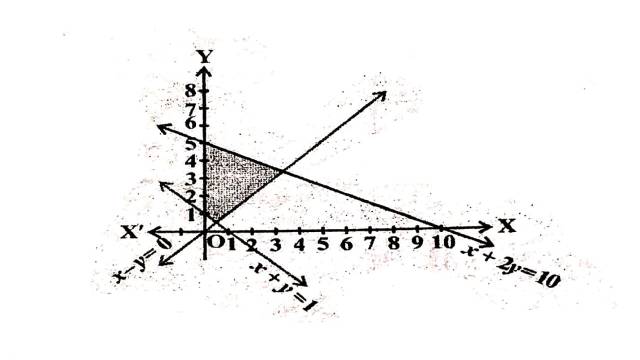
Illustration:15. x+2 y \leq 10, x+y \geq 1,x-y \leq 0,x \geq 0,y \geq 0
Solution: x+2 y \leq 10, x+y \geq 1,x-y \leq 0,x \geq 0,y \geq 0
दी गई असमिकाओं के संगत समीकरण हैं:
x+2y=10,x+y=1,x-y=0,y=0,x=0
x+2y=10 अक्षों को (10,0) तथा (0,5) पर मिलती है।बिन्दुओं को गहरी रेखा द्वारा मिलाते हैं।मूलबिन्दु असमिका x+2 y \leq 10 \Rightarrow 0+2(0) \leq 10 \Rightarrow 0 \leq 10 को सन्तुष्ट करता है।इसलिए रेखा पर स्थित बिन्दुओं सहित मूलबिन्दु हल क्षेत्र में समाविष्ट है।
x+y=1 अक्षों को (1,0) तथा (0,1) पर मिलती है।बिन्दुओं को गहरी रेखा द्वारा मिलाते हैं।मूलबिन्दु असमिका x+y \geq 1 \Rightarrow 0+0 \geq 1 \Rightarrow 0 \geq 1 को सन्तुष्ट नहीं करता है।इसलिए मूलबिन्दु हल क्षेत्र में समाविष्ट नहीं है।अतः हल क्षेत्र रेखा x+y=1 पर स्थित बिन्दुओं सहित मूलबिन्दु से विपरीत ओर स्थित है।
x-y=0 मूलबिन्दु,प्रथमपाद व तृतीय पाद से होकर गुजरती है।मूलबिन्दु असमिका x-y \leq 0 \Rightarrow 0-0 \leq 0 \Rightarrow 0 \leq 0 को सन्तुष्ट करती है।इसलिए हल क्षेत्र मूलबिन्दु से रेखा के ऊपर की ओर स्थित है।
स्पष्टतः x \geq 0 तथा y \geq 0 प्रथम पाद को प्रदर्शित करते हैं।
अतः दी गई असमिकाओं का उभयनिष्ठ हल क्षेत्र चित्र में छायांकित भाग द्वारा दर्शाया गया है।
उपर्युक्त उदाहरणों के द्वारा दो चर राशियों की रैखिक असमिकाएँ (Linear Inequality in Two Variables in Two Variables),दो चर राशियों की रैखिक असमिका निकाय का हल कक्षा 11 (Solution of System of Linear Inequalities in Two Variables Class 11) को समझ सकते हैं।
3.दो चर राशियों की रैखिक असमिकाओं के सवाल (Linear Inequality in Two Variables in Two Variables Questions):
निम्नलिखित असमिकाओं का लेखाचित्र विधि से हल क्षेत्र ज्ञात कीजिए:
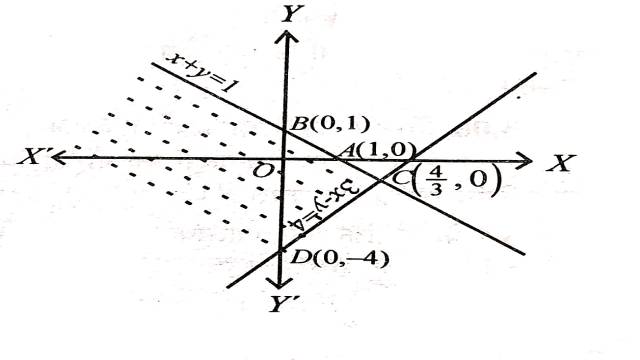
(1.) x+y तथा 3 x-y<4
(2.) 3 x+4 y \leq 12,4 x+3 y \leq 12, x \geq 0, y \geq 0
उत्तर (Answers): (1) असमिकाओं का उभयनिष्ठ हल क्षेत्र चित्र में छायांकित भाग द्वारा दर्शाया गया है।
(2)असमिकाओं का उभयनिष्ठ हल क्षेत्र चित्र में छायांकित भाग द्वारा दर्शाया गया है।
उपर्युक्त सवालों को हल करने पर दो चर राशियों की रैखिक असमिकाएँ (Linear Inequality in Two Variables in Two Variables),दो चर राशियों की रैखिक असमिका निकाय का हल कक्षा 11 (Solution of System of Linear Inequalities in Two Variables Class 11) को ठीक से समझ सकते हैं।
Also Read This Article:- Linear Inequalities in Two Variables
4.दो चर राशियों की रैखिक असमिकाएँ (Frequently Asked Questions Related to Linear Inequality in Two Variables in Two Variables),दो चर राशियों की रैखिक असमिका निकाय का हल कक्षा 11 (Solution of System of Linear Inequalities in Two Variables Class 11) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.असमिका के सामान्य गुणधर्म बताइए। (Describe the General Properties of Inequalities):
उत्तर:(1.)असमिका के दोनों पक्षों में समान संख्या जोड़ने अथवा घटाने पर असमिका का चिन्ह अपरिवर्तित रहता है। (2.)किसी असमिका के दोनों पक्षों को किसी समान धनात्मक संख्या से गुणा करने अथवा भाग देने पर असमिका का चिन्ह अपरिवर्तित रहता है। (3.)किसी असमिका के दोनों पक्षों को किसी ऋणात्मक संख्या से गुणा करने अथवा भाग देने पर असमिका का चिन्ह बदल जाता है। उदाहरण: x+y<5 \Rightarrow -3(x+y)>-15
(4.)किसी असमिका में कोई पद एक पक्ष से दूसरे पक्ष में ले जाते हैं,तब पद का चिन्ह बदल देते हैं।
प्रश्न:2.रैखिक असमिकाओं को हल करने की क्रियाविधि लिखिए। (Explain the Working Rule of Solving Linear Inequalities):
उत्तर:(1.)दी गई असमिका में प्रयुक्त चिन्ह >,<, \geq, \leq को हटाकर बराबर का चिन्ह लगाकर संगत समीकरण में बदलते हैं,जो कि xy-समतल में एक सरल रेखा को निरूपित करती है।
(2.) पद (1.) से प्राप्त समीकरण में y=0 रखकर एक बिन्दु ज्ञात करते हैं,जहाँ रेखा x-अक्ष को मिलती है,इसी प्रकार x=0 रखकर एक बिन्दु ज्ञात करते हैं,जहाँ रेखा y-अक्ष को मिलती है।
(3.)पद (2.) से प्राप्त बिन्दुओं को मिलाने पर एक सरल रेखा प्राप्त होती है,जो दी गई असमिका से प्राप्त सरल रेखा को निरूपित करती है।यदि असमिका में \geq अथवा \leq हो तब गहरी काली रेखा खींचते है,अन्यथा हल्की रेखा खींचते हैं।
(4.)सरल रेखा ग्राफ पेपर को दो भागों में विभक्त करती है।अब दी गई असमिका में x=0 तथा y=0 रखते हैं,यदि यह मान असमिका को सन्तुष्ट करता है,तब मूलबिन्दु की ओर का भाग असमिका का हल क्षेत्र होगा अर्थात् हल क्षेत्र में मूलबिन्दु समाविष्ट होगा।यदि यह मान असमिका को सन्तुष्ट नहीं करता है तब मूलबिन्दु के विपरीत ओर का भाग हल क्षेत्र होगा,अर्थात् हल क्षेत्र में मूलबिन्दु समाविष्ट नहीं होगा।हल क्षेत्र को छायांकित नहीं करते हैं।
(5.)यदि असमिका में \geq अथवा \leq हो तब रेखा पर स्थित बिन्दु भी हल क्षेत्र में समाविष्ट होते हैं,अन्यथा हल क्षेत्र में समाविष्ट न माने जाएं।
(6.)यदि एक से अधिक असमिकाएँ हों,तब उभयनिष्ठ हल क्षेत्र ज्ञात किया जाता है।यह उभयनिष्ठ हल क्षेत्र सभी असमिकाओं को सन्तुष्ट करता है।इस क्षेत्र का प्रत्येक बिन्दु असमिकाओं को सन्तुष्ट करता है।उभयनिष्ठ हल क्षेत्र को छायांकित करते हैं।यदि ऐसा कोई उभयनिष्ठ भाग प्राप्त नहीं हो जो सभी असमिकाओं को सन्तुष्ट करता हो,तब इन असमिकाओं का कोई वास्तविक हल सम्भव नहीं है।
प्रश्न:3.क्रान्तिक बिन्दु कैसे ज्ञात करते हैं? (How to Find Critical Points?):
उत्तर:सभी गुणनखण्डों की शून्य से तुलना करने पर x या y के जो मान प्राप्त होते हैं उन्हें क्रान्तिक बिन्दु कहते हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा दो चर राशियों की रैखिक असमिकाएँ (Linear Inequality in Two Variables in Two Variables),दो चर राशियों की रैखिक असमिका निकाय का हल कक्षा 11 (Solution of System of Linear Inequalities in Two Variables Class 11) के बारे में और अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Linear Inequality in Two Variables
दो चर राशियों की रैखिक असमिकाएँ
(Linear Inequality in Two Variables)
Linear Inequality in Two Variables
दो चर राशियों की रैखिक असमिकाएँ (Linear Inequality in Two Variables) के इस
आर्टिकल में दो चर राशियों की असमिका निकाय पर आधारित सवालों को लेखाचित्र विधि
से हल ज्ञात करना सीखेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.