1.कलन में समतल वक्रों की लम्बाई (Length of Plane Curves Calculus),समतल वक्रों की लम्बाई (Length of Plane Curves):

• कलन में समतल वक्रों की लम्बाई (Length of Plane Curves Calculus) ज्ञात करने का अध्ययन हम पूर्व आर्टिकल में कर चुके हैं।समतल वक्र के दो बिन्दुओं के बीच चाप (arc) की लम्बाई ज्ञात करने की विधि को चापकलन (Rectification) भी कहते हैं।इस आर्टिकल में कुछ ओर उदाहरणों के द्वारा चाप की लम्बाई ज्ञात करने का अध्ययन करेंगे।
  
• आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
  

Also Read This Article:Rectification in Integral Calculus

2.कलन में समतल वक्रों की लम्बाई पर आधारित उदाहरण (Examples Based on Length of Plane Curves Calculus):

Example:1.प्रदर्शित कीजिए कि वक्र x^{2}=a^{2}\left(1-e^{\frac{y}{a}}\right) के बिन्दु (0,0) से (x,y) तक नापे गए चाप की लम्बाई a{\log{\left(\frac{a+x}{a-x}\right)}}-x है।
(Show that the length of the arc of the curve x^{2}=a^{2}\left(1-e^{\frac{y}{a}}\right) measured from a{\log{\left(\frac{a+x}{a-x}\right)}}-x is.)
Solution:x^{2}=a^{2}\left(1-e^{\frac{y}{a}}\right)
\Rightarrow{e^{\frac{y}{a}}}=1-\frac{x^{2}}{a^{2}}
x के सापेक्ष अवकलन करने पर:
\frac{1}{a}{e{\frac{y}{a}}}{\frac{dy}{dx}}=\frac{-2a}{a^{2}}
\Rightarrow{\frac{dy}{dx}}=\frac{-2x}{a{\left(1-{\frac{x^{2}}{a^{2}}}\right)}}    [(1) से]
\Rightarrow{\frac{dy}{dx}}=\frac{-2ax}{a^{2}-x^{2}}
अभीष्ट चाप की लम्बाई s=\int_{0}^{x} { \sqrt { 1+{ \left( \frac { dy }{ dx } \right) }^{ 2 } } } dx
=\int_{0}^{x}{\sqrt{1+\frac{4a^{2}x^{2}}{{\left(a^{2}-x^{2}\right)}^{2}}}}dx
=\int_{0}^{x}{\sqrt{\frac{a^{4}+x^{4}-2a^{2}x^{2}+4a^{2}x^{2}}{{\left(a^{2}-x^{2}\right)}^{2}}}}dx
=\int_{0}^{x}{\sqrt{\frac{a^{4}+x^{4}+2a^{2}x^{2}}{{\left(a^{2}-x^{2}\right)}^{2}}}}dx
=\int_{0}^{x}{\frac{\sqrt{{\left(a^{2}+x^{2}\right)}^{2}}}{a^{2}-x^{2}}}dx
=\int_{0}^{x}{\frac{a^{2}+x^{2}}{a^{2}-x^{2}}}dx
=\int_{0}^{x}{\left(\frac{2a^{2}}{a^{2}-x^{2}}-1\right)}dx
=\int_{0}^{x}{\frac{2a^{2}}{a^{2}-x^{2}}}dx-{\int_{0}^{x}{1}dx}
=\left[a{\log{\left(\frac{a+x}{a-x}\right)}}\right]_{0}^{x}-\left[x\right]_{0}^{x}

=a{\log{\left(\frac{a+x}{a-x}\right)}}-x
Example:2.प्रदर्शित कीजिए कि (0,a) से (x,y) तक नापी गई वक्र x^{\frac{2}{3}}+y^{\frac{2}{3}}=a^{\frac{2}{3}} की लम्बाई \frac{3}{2}{\left(ax^{2}\right)}^{\frac{1}{3}} है।
(Show that the length of the curve x^{\frac{2}{3}}+y^{\frac{2}{3}}=a^{\frac{2}{3}} measured from (0,a) to the point (x,y) is \frac{3}{2}{\left(ax^{2}\right)}^{\frac{1}{3}})

Solution:x^{\frac{2}{3}}+y^{\frac{2}{3}}=a^{\frac{2}{3}}
\Rightarrow{y^{\frac{2}{3}}}=a^{\frac{2}{3}}-x^{\frac{2}{3}}
x के सापेक्ष अवकलन करने पर:
\frac{2}{3}{y^{\frac{-1}{3}}}{\frac{dy}{dx}}=-\frac{2}{3}{x^{\frac{-1}{3}}}
\Rightarrow{\frac{dy}{dx}}=-{\frac{x^{\frac{-1}{3}}}{y^{\frac{-1}{3}}}}
\Rightarrow{\frac{dy}{dx}}=-{\frac{y^{\frac{1}{3}}}{x^{\frac{1}{3}}}}
\Rightarrow{1+{\left(\frac{dy}{dx}\right)}^{2}}=1+{\frac{y^{\frac{2}{3}}}{x^{\frac{2}{3}}}}
\Rightarrow{1+{\left(\frac{dy}{dx}\right)}^{2}}=\frac{x^{\frac{2}{3}}+{y^{\frac{2}{3}}}}{x^{\frac{2}{3}}}
\Rightarrow{1+{\left(\frac{dy}{dx}\right)}^{2}}=\frac{a^{\frac{2}{3}}}{x^{\frac{2}{3}}}
अभीष्ट चाप की लम्बाई s=\int_{0}^{x} { \sqrt { 1+{ \left( \frac { dy }{ dx } \right) }^{ 2 } } } dx

=\int_{0}^{x}\sqrt{\frac{a^{\frac{2}{3}}}{x^{\frac{2}{3}}}}dx
=\int_{0}^{x}{\frac{1}{x^{\frac{1}{3}}}}dx
=\int_{0}^{x}{x^{\frac{-1}{3}}}dx
=a^{\frac{1}{3}}{\frac{3}{2}}{\left[x^{\frac{2}{3}}\right]}_{0}^{x}

=\frac{3}{2}{\left(ax^{2}\right)}^{\frac{1}{3}}

Example:3.प्रदर्शित कीजिए कि वक्र के एक चाप की लम्बाई Show that the length of an arc of the curve

x\sin{\theta}+y\cos{\theta}=f'{\left(\theta\right)},x\cos{\theta}-y\sin{\theta}=f''{\left(\theta\right)}

निम्नलिखित प्रतिबन्ध द्वारा दी जाती है is given by the following relation

s=f\left(\theta\right)+f''{\left(\theta\right)}+C

Solution:x\sin{\theta}+y\cos{\theta}=f'{\left(\theta\right)}  ….(1) x\cos{\theta}-y\sin{\theta}=f''{\left(\theta\right)}    …(2)

समीकरण (1) का \theta{} के सापेक्ष अवकलन करने पर:

\frac{dx}{d\theta}{\sin{\theta}}+x\cos{\theta}+\frac{dy}{d\theta}{\cos{\theta}}-y\sin{\theta}=f"{\left(\theta\right)}

(2) से मान रखने पर:

\Rightarrow{\frac{dx}{d\theta}}\sin{\theta}+\frac{dy}{d\theta}{\cos{\theta}}+f"{\left(\theta\right)}=f"{\left(\theta\right)}
\Rightarrow{\frac{dx}{d\theta}}+\frac{dy}{d\theta}{\cos{\theta}}=0

समीकरण (2) का \theta{} के सापेक्ष अवकलन करने पर:

\frac{dx}{d\theta}{\cos{\theta}}-x\sin{\theta}-\frac{dy}{d\theta}{\sin{\theta}}-y\cos{\theta}=f"'{\left(\theta\right)}

समीकरण (1) से मान रखने पर:

\frac{dx}{d\theta}{\cos{\theta}}-\frac{dy}{d\theta}{\sin{\theta}}-f'{\left(\theta)\right)}=f"'{\left(\theta\right)}
\frac{dx}{d\theta}{\cos{\theta}}-\frac{dy}{d\theta}{\sin{\theta}}=f'{\left(\theta)\right)}+f"'{\left(\theta\right)}

समीकरण (3) व (4) का वर्ग करके जोड़ने पर:

\left(\frac{dx}{d\theta}{\sin{\theta}}+\frac{dy}{d\theta}{\cos{\theta}}\right)^{2}+\left(\frac{dx}{d\theta}{\cos{\theta}}-\frac{dy}{d\theta}{\sin{\theta}}\right)^{2}=\left[f'{\left(\theta\right)}+f"'{\left(\theta\right)}\right]^{2}
\Rightarrow{\left(\frac{dx}{d\theta}\right)}^{2}{\sin^{2}{\theta}}+\left(\frac{dy}{d\theta}\right)^{2}{\cos^{2}{\theta}}+2\left(\frac{dx}{d\theta}\right){\left(\frac{dy}{d\theta}\right)\sin{\theta}\cos{\theta}+\left(\frac{dx}{d\theta}\right)}^{2}{\cos^{2}{\theta}}+\left(\frac{dy}{d\theta}\right)^{2}{\sin^{2}{\theta}}-2\left(\frac{dx}{d\theta}\right){\left(\frac{dy}{d\theta}\right)\sin{\theta}\cos{\theta}}=\left[f'{\left(\theta\right)}+f"{\left(\theta\right)}\right]^{2}
\Rightarrow{\left(\frac{dx}{d\theta}\right)}^{2}{\left(\sin^{2}{\theta}+\cos^{2}{\theta}\right)}+\left(\frac{dy}{d\theta}\right)^{2}{\cos^{2}{\theta}+\sin^{2}{\theta}}=\left[f'{\left(\theta\right)}+f"{\left(\theta\right)}\right]^{2}
\Rightarrow{\left(\frac{dx}{d\theta}\right)^{2}+\left(\frac{dy}{d\theta}\right)^{2}}=\left[f'{\left(\theta\right)}+f"{\left(\theta\right)}\right]^{2}

अतः अभीष्ट चाप की लम्बाई s=\int{\sqrt{\left[f'{\left(\theta\right)}+f"{\left(\theta\right)}\right]}^{2}}

s=\int{\left[f'{\left(\theta\right)}+f"{\left(\theta\right)}\right]}d\theta

=f\left(\theta\right)+f"{\left(\theta\right)}+C

Example:4.सिद्ध कीजिए कि वक्र के चाप की लम्बाई (Prove that the length of the arc of the curve) x=a\sin{2\theta}{\left(1+cos{2\theta}\right)},y=a\cos{2\theta}{\left(1-\cos{2\theta}\right)} जो कि (0,0) से किसी बिन्दु (x,y) तक नापा गया है,{\frac{4}{3}}a\sin{3\theta} के बराबर है। (Which is measured from (0,0) to any point (x,y) is equal to {\frac{4}{3}}a\sin{3\theta}.)

Solution:x=a\sin{2\theta}{\left(1+cos{2\theta}\right)}  …(1)

y=a\cos{2\theta}{\left(1-\cos{2\theta}\right)} …(2)

समीकरण (1) का \theta{} के सापेक्ष अवकलन करने पर:

\frac{dx}{d\theta}=2a\cos{2\theta}\left(1+\cos{2\theta}\right)-2a\sin^{2}{2\theta}

=2a\cos{2\theta}+2a^{2}{\cos^{2}{2\theta}}  ….(3} समीकरण (2) के \theta{} सापेक्ष अवकलन करने पर:

\frac{dy}{d\theta}=-2a\sin{2\theta}{\left(1-\cos{2\theta}\right)}+2a\cos{2\theta}\sin{2\theta}

=-2a\sin{2\theta}+2a\sin{2\theta}\cos{2\theta}+2a\cos{2\theta}\sin{2\theta}

\frac{dy}{d\theta}=-2a\sin{2\theta}+4a\sin{2\theta}\cos{2\theta}

समीकरण (3) व (4) का वर्ग करके जोड़ने पर:

\left(\frac{dx}{d\theta}\right)^{2}+\left(\frac{dy}{d\theta}\right)=\left[2a\cos{2\theta}+2a\cos^{2}{2\theta}-2a\sin^{2}{2\theta}\right]^{2}+\left[-2\sin{2\theta}+4a\sin{2\theta}\cos{2\theta}\right]^{2}

=4a^{2}\cos^{2}{2\theta}+4a^{2}\cos^{4}{2\theta}+4a^{2}\sin^{4}{2\theta}+8a^{2}\cos^{3}{2\theta}-8a^{2}\cos^{2}{2\theta}sin^{2}{2\theta}-8a^{2}\cos{2\theta}sin^{2}{2\theta}+4a^{2}\sin^{2\theta}+16a^{2}\sin^{2}{2\theta}\cos^{2}{2\theta}-16a^{2}\sin^{2}{2\theta}\cos{2\theta} =4a^{2}\left(\sin^{2}{2\theta}+\cos^{2}{2\theta}\right)+4a^{2}\left(\cos^{4}{2\theta}+\sin^{4}{2\theta}+2\sin^{2}{2\theta}\cos^{2}{2\theta}\right)+8a^{2}\cos^{3}{2\theta}-24a^{2}\sin^{2}{2\theta}\cos{2\theta}

=4a^{2}+4a^{2}\left(\sin^{2}{2\theta}+\cos^{2}{2\theta}\right)^{2}+8a^{2}\cos^{3}{2\theta}-24a^{2}\sin^{2}{2\theta}\cos{2\theta}

=4a^{2}+4a^{2}+8a^{2}\cos^{3}{2\theta}-24a^{2}\sin^{2}{2\theta}\cos{2\theta}

=8a^{2}+8a^{2}\cos^{3}{2\theta}-24a^{2}\left(1-\cos^{2}{2\theta}\right)\cos{2\theta}

=8a^{2}+8a^{2}\cos^{3}{2\theta}-24a^{2}\cos{2\theta}+24a^{2}\cos^{3}{2\theta}

=8a^{2}+32a^{2}\cos^{3}{2\theta}-24a^{2}\cos{2\theta}

=8a^{2}+32a^{2}\cos^{3}{2\theta}-24a^{2}\cos{2\theta}

=8a^{2}+32a^{2}\left(2\cos^{2}{\theta}-1\right)^{3}-24a^{2}\left(2cos^{2}{\theta}-1\right) =8a^{2}+256a^{2}\cos^{6}{\theta}-384a^{2}cos^{4}{\theta}+192a^{2}\cos^{2}{\theta}-32a^{2}-48a^{2}\cos^{2}{\theta}+24a^{2}

=256a^{2}\cos^{6}{\theta}-384a^{2}\cos^{4}{\theta}+144a^{2}\cos^{2}{\theta}

=16a^{2}\left(16cos^{6}{\theta}-24\cos^{4}{\theta}+9\cos^{2}{\theta}\right)

=16a^{2}\left(4\cos^{3}{\theta}-3\cos{\theta}\right)^{2}

=16a^{2}\cos^{2}{3\theta}

\Rightarrow{\left(\frac{dx}{d\theta}\right)^{2}+\left(\frac{dy}{d\theta}\right)}^{2}=16a^{2}\cos^{2}{3\theta}

अभीष्ट चाप की लम्बाई s=s=\int { \sqrt { { \left( \frac { dx }{ dt } \right) }^{ 2 }+{ \left( \frac { dy }{ dt } \right) }^{ 2 } } } dt

\int_{0}^{\theta}{\sqrt{16a^{2}\cos^{2}{3\theta}}}{d\theta}

4a\int_{0}^{\theta}{\cos{3\theta}}{d\theta}
=\frac{4a}{3}\sin{3\theta}
Example:5.यदि छोटा हो तो सिद्ध कीजिए कि लिमेकन r=a+b\cos{\theta} की परिमाप का सन्निकटन मान 2{\pi}{a}\left(1+{\frac{1}{4}}{\frac{b^{2}}{a^{2}}}\right) होगा।
(Prove that the perimeter of the limacon r=a+b\cos{\theta},if be small,is approximately 2{\pi}{a}\left(1+{\frac{1}{4}}{\frac{b^{2}}{a^{2}}}\right).)

Solution:\frac{b}{a}छोटा है अतः a>b
r=a+b\cos{\theta}   …(1)
(1) का \theta{} के सापेक्ष अवकलन करने पर:
\frac{dr}{d\theta}=-b\sin{\theta}
=r^{2}+\left(\frac{dr}{d\theta}\right)^{2}=\left(a+b\cos{\theta}\right)^{2}+\left(-b\sin{\theta}\right)^{2}
=a^{2}+b^{2}\cos^{2}{\theta}+2ab\cos{\theta}+b^{2}\sin^{2}{\theta}
=a^{2}+2ab\cos{\theta}+b^{2}\left(cos^{\theta}+sin^{2}{\theta}\right)^{2}
=a^{2}+2ab\cos{\theta}+b^{2}
=a^{2}\left(1+\frac{2b}{a}\cos{\theta}+\frac{b^{2}}{a^{2}}\right)
अभीष्ट चाप की लम्बाई s=\int_{0}^{\pi} { \sqrt { { r }^{ 2 }+{ \left( \frac { dr }{ d\theta } \right) }^{ 2 } } } d\theta
=2\int_{0}^{\pi}{\left(1+\frac{2b}{a}+\frac{b^{2}}{a^{2}}\right)}^{\frac{1}{2}}
=2\int_{0}^{\pi}\left[1+\frac{b}{a}\cos{\theta}+\frac{1}{2}\frac{b^{2}}{a^{2}}+\frac{{\frac{1}{2}}{\left(\frac{-1}{2}\right)}}{2!}{\left(\frac{4b^{2}}{a^{2}}\cos^{2}{\theta}\right)}\right]{d\theta}
\frac{b}{a} की उच्चतम घातों को छोड़ने पर]
=2a\int_{0}^{\pi}{\left[1+\frac{b}{a}\cos{\theta}+{\frac{1}{2}}{\frac{b^{2}}{a^{2}}}{\left(1-\cos^{2}{\theta}\right)}\right]}{d\theta}
=2a\int_{0}^{\pi}{\left[1+\frac{b}{a}\cos{\theta}+{\frac{1}{2}}{\frac{b^{2}}{a^{2}}}{\sin^{2}{\theta}}\right]}{d\theta}
=2a\int_{0}^{\pi}{\left[1+\frac{b}{a}\cos{\theta}+{\frac{b^{2}}{4a^{2}}}{\left(1-\cos{2\theta}\right)}\right]}{d\theta}
=2a\left[{\theta}+\frac{b}{a}\sin{\theta}+\frac{b^{2}}{4a^{2}}{\theta}-{\frac{b^{2}}{8a^{2}}}{\sin{2\theta}}\right]_{0}^{\pi}

=2a{\pi}{\left[1+\frac{b^{2}}{4a^{2}}\right]}

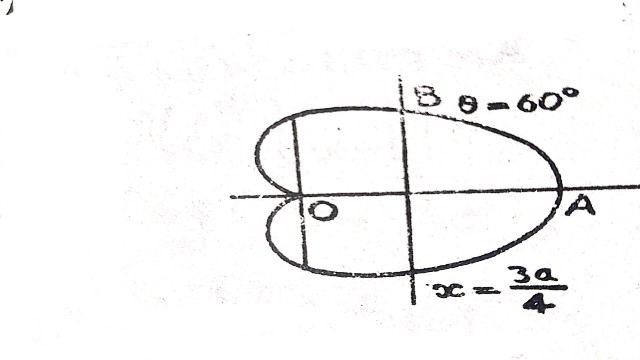
Example:6.सिद्ध कीजिए कि कार्डिआइड r=a\left(1+\cos{\theta}\right) रेखा 4r\cos{\theta}=3a द्वारा ऐसे दो भागों में विभाजित होता है कि लम्बाईयाँ बराबर हैं। (Prove that cardiod r=a\left(1+\cos{\theta}\right) is divided by the line 4r\cos{\theta}=3a into two parts such that the lengths of arcs on either way of that line are equal.)

Solution:r=a\left(1+\cos{\theta}\right) …(1) \theta{} के सापेक्ष अवकलन करने पर:

\frac{dr}{d\theta}=-a\sin{\theta}

=r^{2}+\left(\frac{dr}{d\theta}\right)^{2}=a^{2}{\left(1+\cos{\theta}\right)}^{2}+\left(-a\sin{\theta}\right)^{2} =a^{2}{\left(1+\cos^{2}{\theta}+2\cos{\theta}+\sin^{2}{\theta}\right)} =a^{2}{\left(1+2\cos{\theta}+1\right)} =a^{2}{\left(2+2\cos{\theta}\right)} =2a^{2}{\left(1+\cos{\theta}\right)} =2a^{2} × 2\cos^{2}{\frac{\theta}{2}} =4a^{2} {\cos^{2}{\frac{\theta}{2}}}

अभीष्ट चाप की लम्बाई =s=\int_{0}^{\pi} { \sqrt { { r }^{ 2 }+{ \left( \frac { dr }{ d\theta } \right) }^{ 2 } } } d\theta

2\int_{0}^{\pi}{sqrt{4a^{2} {\cos^{2}{\frac{\theta}{2}}}}}{d\theta}

4a\int_{0}^{\pi}{\cos{\frac{\theta}{2}}}{d\theta}

4a ×2 \left[\sin{\frac{\theta}{2}}\right]_{0}^{\pi}

=8a

4r\cos{\theta}=3a या x=\frac{3a}{2}

प्रारंभिक रेखा पर लम्बवत् है जो ध्रुव (मूलबिन्दु) से x=\frac{3a}{2} दूरी पर है। समीकरण (1) व (2) से r का विलोपन करने पर:

a\left(1+\cos{\theta}\right)=\frac{3a}{4\cos{\theta}}
\Rightarrow{4\cos{\theta}+4\cos^{2}{\theta}-3=0}
\Rightarrow{4\cos^{2}{\theta}+4\cos{\theta}-3=0}
\Rightarrow{4\cos^{2}{\theta}+6\cos{\theta}-2\cos{\theta}-3=0}
\Rightarrow{2\cos{\theta}\left(2\cos{\theta}+3\right)-1\left(2\cos{\theta}+3\right)=0}
\Rightarrow{\left(2\cos{\theta}-1\right)\left(2\cos{\theta}+3\right)=0}
\Rightarrow{\cos{\theta}=\frac{1}{2}}
\Rightarrow{\theta}=\frac{\pi}{3}

अतः सीमा 0 से \frac{\pi}{3} लेने पर: =

\Rightarrow {8a\left[\sin{\frac{\theta}{2}}\right]_{0}^{\pi}}

\Rightarrow{8a\sin{\frac{\pi}{6}}}
=8a × \frac{1}{2}
=4a
अतः दो भागों में विभाजित होता है।
उपर्युक्त उदाहरणों के द्वारा कलन में समतल वक्रों की लम्बाई (Length of Plane Curves Calculus),समतल वक्रों की लम्बाई (Length of Plane Curves) को समझ सकते हैं।

Also Read This Article:Lengths of Plane Curves

3.कलन में समतल वक्रों की लम्बाई (Length of Plane Curves Calculus),समतल वक्रों की लम्बाई (Length of Plane Curves) के सम्बन्ध में अक्सर पूछे जाने पर प्रश्न:

• उपर्युक्त प्रश्नों के उत्तर द्वारा कलन में समतल वक्रों की लम्बाई (Length of Plane Curves Calculus),समतल वक्रों की लम्बाई (Length of Plane Curves) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।

Length of Plane Curves Calculus

कलन में समतल वक्रों की लम्बाई
(Length of Plane Curves Calculus)

Length of Plane Curves Calculus

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Instagram	click here
4.	Linkedin	click here
5.	Facebook Page	click here
6.	Twitter	click here