Inequalities of Triangle in Class 9
1.त्रिभुज में असमिकाएं कक्षा 9 (Inequalities of Triangle in Class 9),त्रिभुज की असमिका का प्रमाण (Proof of Triangle Inequality):
त्रिभुज में असमिकाएं कक्षा 9 (Inequalities of Triangle in Class 9) के इस आर्टिकल में किसी त्रिभुज में असमान भुजाओं और असमान कोणों में सम्बन्ध का अध्ययन करेंगे।सर्वप्रथम त्रिभुज में असमिकाओं की प्रमेय का अध्ययन करेंगे।
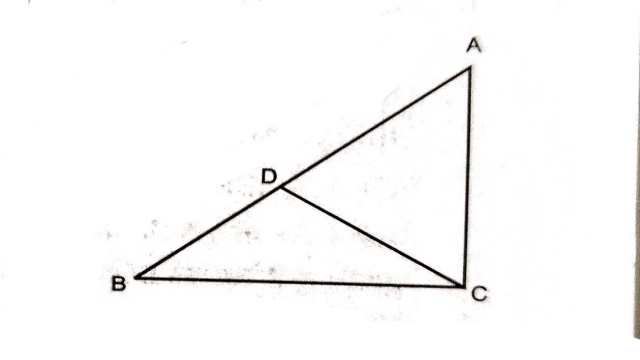
प्रमेय (Theorem):7.6.यदि किसी त्रिभुज की दो भुजाएँ असमान हों तो लम्बी भुजा के सामने का सम्मुख कोण बड़ा होता है।
दिया है (Given):त्रिभुज ABC में AB>AC
सिद्ध करना है (To Prove): \angle C > \angle B
रचना (Construction):शीर्ष C से CD रेखा इस प्रकार खींची कि AC=AD हो।
उपपत्ति (Proof):रचना से में भुजा AC=AD समान है अतः इनके सम्मुख कोण भी समान होंगे।
\angle ACD=\angle ADC \cdots(1) \\ \because \angle ADC त्रिभुज BDC का बहिष्कोण है
अतः \angle ADC>\angle B \cdots(2)
(1) व (2) सेः
\angle ACD>\angle B \cdots(3)
चित्र सेः \angle ACB> \angle ACB \cdots(4)
(3) व (4) सेः
\angle ACB>\angle ACB>\angle B \\ \Rightarrow \angle A C B>\angle B \\ \Rightarrow \angle C>\angle B
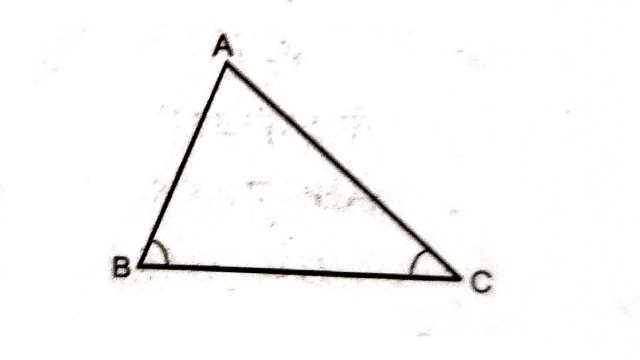
प्रमेय (Theorem):7.7.(प्रमेय 7.6) का विलोम) किसी त्रिभुज में बड़े कोण की सम्मुख भुजा बड़ी (लम्बी) होती है।
दिया है (Given):त्रिभुज ABC में \angle B>\angle C
सिद्ध करना है (To Prove):AC>AB
उपपत्ति (Proof): \triangle ABC की भुजा AC एवं AB के लिए निम्नलिखित तीन सम्भावनाएं हो सकती हैं जिनमें से केवल एक ही सत्य हो सकती है।
(i)AC=AB (ii)AC < AB (iii)AC > AB
स्थिति (i):जब AC=AB हो
यदि AC=AB हो तो \triangle ABC में समान भुजाओं के सम्मुख कोण समान होंगे अर्थात् \angle B =\angle C जो कि असंभव है क्योंकि दिया हुआ है कि \angle B>\angle C
अतः AC \neq AB
स्थिति (ii):जब AC < AB हो
हम जानते है कि बड़ी भुजा के सामने का कोण बड़ा होता है अतः AC < AB \Rightarrow \angle C < \angle B
जो दिए गए तथ्य का विरोधाभासी है अतः AC \not < AB
स्थिति (iii):जब AC > AB हो
अब हमारे पास केवल तीसरी संभावना शेष है जो अवश्य सत्य होगी अर्थात्
AC>AB
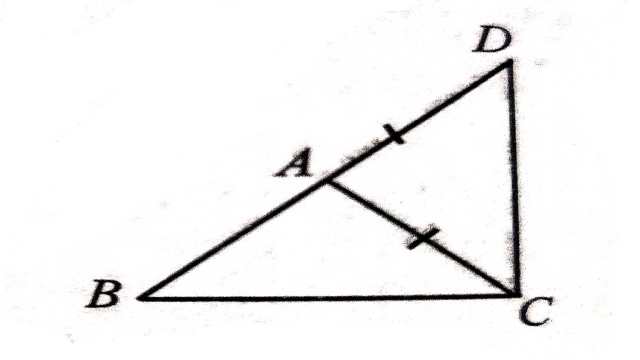
प्रमेय (Theorem):7.8.त्रिभुज की किन्हीं दो भुजाओं का योग तीसरी भुजा से बड़ा होता है।
दिया है (Given):एक \triangle ABC है।
सिद्ध करना है (To Prove):(i)AB+BC>AC
(ii)BC+AC>AB
(iii)AC+AB>BC
रचना (Construction):भुजा BA को D तक इस प्रकार आगे बढ़ाया कि AD=AC हो।
उपपत्ति (Proof): \triangle ADC में रचना से AD=AC है अतः इनके सम्मुख कोण बराबर होंगे।
अतः \angle ACD=\angle ADC \cdots(1)
एवं \angle BCD>\angle ACD \cdots(2)
(1) व (2) सेः
\angle BCD>\angle ADC=\angle BDC
अतः BD>BC [क्योंकि बड़े कोण की सम्मुख भुजा बड़ी होती है]
अतः BD>BC
BA+AD>BC [BD=BA+BD]
BA+AC>BC [AD=AC (रचना से)]
इसी प्रकार सिद्ध कर सकते हैं कि
AB+BC>AC
BC+AC>AB
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:-Congruence of Triangles Class 9
2.त्रिभुज में असमिकाएं कक्षा 9 के साधित उदाहरण (Inequalities of Triangle in Class 9 Solved Examples):
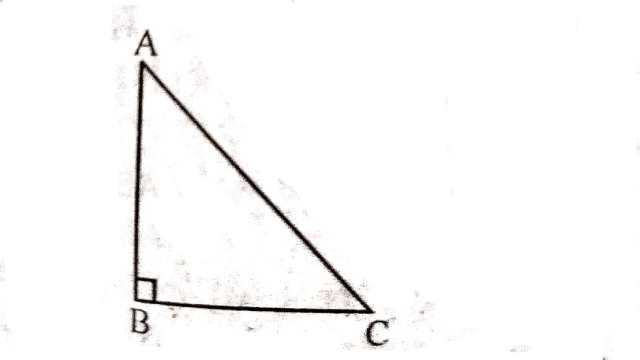
Example:1.दर्शाइए कि समकोण त्रिभुज में कर्ण सबसे लम्बी भुजा होती है।
Solution:दिया है (Given): \triangle ABC में \angle B=90^{\circ}
सिद्ध करना है (To Prove):(i)AC>BC (ii)AC>AB
उपपत्ति (Proof): \angle A+\angle C=90^{\circ}
(समकोण त्रिभुज के दोनों न्यूनकोणों का योग 90° होता है)
\therefore \angle B=\angle A+\angle C \\ \therefore \angle B>\angle A
और \angle B>\angle C \\ \therefore AC>AB (बड़े कोण की सम्मुख भुजा बड़ी होती है)
और AC>BC (बड़े कोण की सम्मुख भुजा बड़ी होती है)
AC सबसे लम्बी भुजा है अर्थात् कर्ण सबसे लम्बी भुजा है।
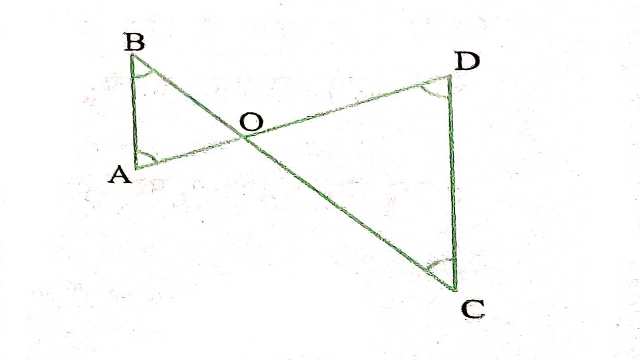
Example:2.आकृति में \angle B < \angle A और \angle C < \angle D है।दर्शाइए कि AD < BC
Solution:दिया है (Given): \angle B < \angle A तथा \angle C < \angle D
सिद्ध करना है (To Prove): AD > BC
उपपत्ति (Proof): \angle B < \angle A(दिया है)
\angle A>\angle B
O B>O A ….(1)
(बड़े कोण की सम्मुख भुजा बड़ी होती है)
\angle C < \angle D \\ \angle D > \angle C
O C>O D …..(2)
(बड़े कोण की सम्मुख भुजा बड़ी होती है)
समीकरण (1) व (2) सेः
OB+OC>OA+OD
\Rightarrow BC>AD
\Rightarrow AD<BC है।
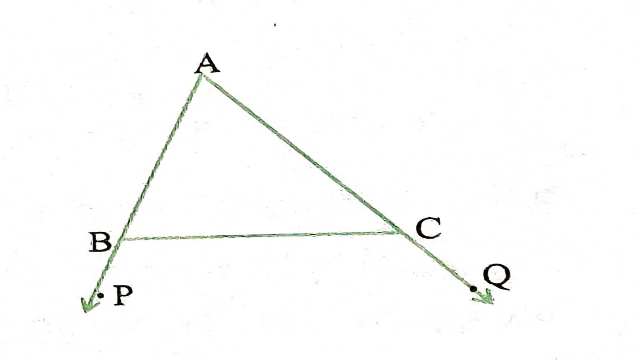
Example:3 आकृति मे \triangle ABC की भुजाओं AB और AC को क्रमशः बिंदुओ P और Q तक बढ़ाया गया है| साथ, ही \angle PBC<\angle QCB है| दर्शाइए कि AC>AB है|
Solution:दिया है (Given): \triangle ABC की भुजाओं AB और AC को क्रमशः बिन्दुओं P और Q तक बढ़ाया गया है।तथा \angle PBC<\angle QCB
सिद्ध करना है (To Prove):AC>AB
उपपत्ति (Proof):\angle PBC=\angle QCB \\ \Rightarrow-\angle PBC>\angle QCB \\ \Rightarrow 180^{\circ}-\angle P B C>180-\angle Q C B \\ \Rightarrow \angle ABC>\angle ACB \\ \therefore AC>A B
(बड़े कोण की सम्मुख भुजा बड़ी होती है)
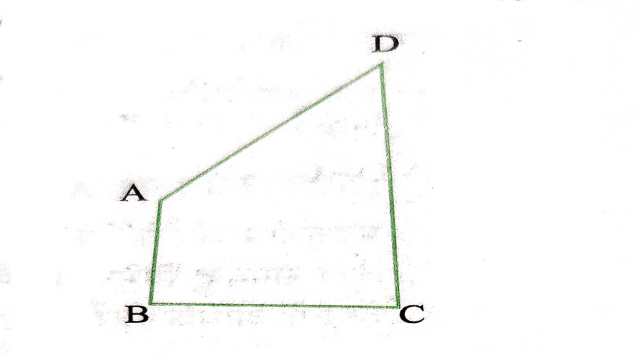
Example:4.AB और CD क्रमशः एक चतुर्भुज ABCD की सबसे छोटी और सबसे बड़ी भुजाएँ हैं (देखिए आकृति)।दर्शाइए कि \angle A>\angle C और \angle B>\angle D हैं।
Solution:दिया है (Given):AB और CD एक चतुर्भुज ABCD की क्रमशः सबसे छोटी और सबसे बड़ी भुजाएँ हैं।
सिद्ध करना है (To Prove): \angle A > \angle C और \angle B > \angle D
रचना (Construction):शीर्ष A से शीर्ष C को मिलाया।
उपपत्ति (Proof): \triangle ABC में
AB <BC
(AB भुजा चतुर्भुज ABCD की सबसे बड़ी भुजा है)
अतः BC > AB
\therefore \angle BAC>\angle BCA \cdots(1)
(बड़ी भुजा के सम्मुख कोण बड़ा होता है)
\triangle ACD में
CD>AD
(\therefore CD भुजा चतुर्भुज ABCD की सबसे लम्बी भुजा है)
\therefore \angle CAD>\angle ACD \cdots(2)
(बड़ी भुजा के सम्मुख कोण बड़ा होता है)
समीकरण (1) व (2) सेः
\angle BAC+\angle CAD>\angle BCA+\angle ACD
अतः \angle A >\angle C
इसी प्रकार B को D से मिलाकर हम सिद्ध कर सकते हैं कि
\angle B>\angle D
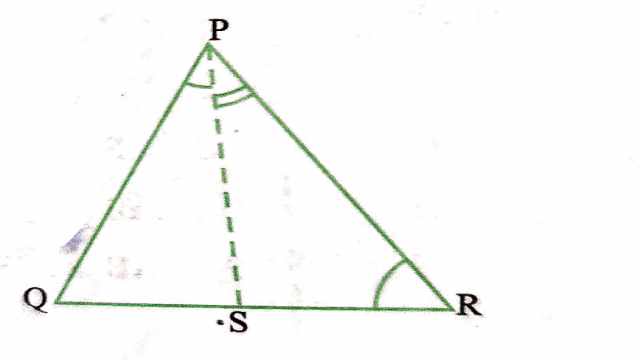
Example:5.आकृति में PR>PQ है और PS कोण QPR को समद्विभाजित करता है।सिद्ध कीजिए कि \angle PSR>\angle PSQ है।
Solution: दिया है (Given): \triangle PQR में PR>PQ और \angle QPR को PS समद्विभाजित करता है।
सिद्ध करना है (To Prove): \angle PSR>\angle PSQ
उपपत्ति (Proof):PR>PQ
\angle Q< \angle R
[\because त्रिभुज में बड़ी भुजा का सम्मुख कोण बड़ा होता है]
अब \angle Q+\angle Q P S>\angle R+\angle R+\angle RPQ
[चूँकि \angle P को PS समद्विभाजित करता है]
इसलिए 180^{\circ}-\angle PSQ>180^{\circ}-\angle PSR
अतः \angle PSR>\angle PSQ
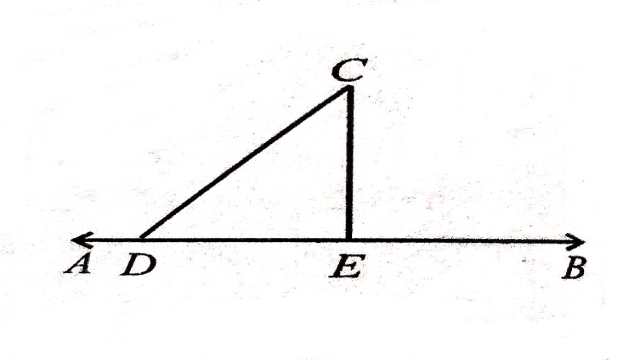
Example:6.दर्शाइए कि एक रेखा पर एक दिए हुए बिन्दु से, जो उस रेखा पर स्थित नहीं है,जितने रेखाखण्ड खींचे जा सकते हैं उनमें लम्ब रेखाखण्ड सबसे छोटा होता है।
Solution:दिया है (Given):रेखाखण्ड AB पर बिन्दु C से रेखाखण्ड CD एवं लम्ब CE को मिलाया।
सिद्ध करना है (To Prove):CE <CD
उपपत्ति (Proof): \triangle CED में
\angle CED=90^{\circ}
अतः \angle CDE < \angle CED
हम जानते है कि बड़े कोण कि सम्मुख भुजा सदैव बड़ी होती है अतः CD>CE
अर्थात् बाह्य बिन्दु से खींचे गए सभी रेखाखण्डों में से लम्बवत रेखाखण्ड ही सबसे छोटा होता है।
उपर्युक्त उदाहरणों के द्वारा त्रिभुज में असमिकाएं कक्षा 9 (Inequalities of Triangle in Class 9),त्रिभुज की असमिका का प्रमाण (Proof of Triangle Inequality) को समझ सकते हैं।
3.त्रिभुज में असमिकाएं कक्षा 9 के सवाल (Inequalities of Triangle in Class 9 Questions):
(1.)\triangle PQR में भुजा QR पर S कोई बिन्दु है।दिखाइए कि PQ+QR+RP>2PS
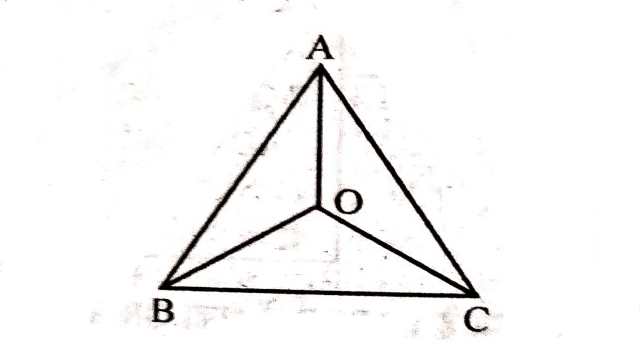
(2.)चित्र में त्रिभुज में कोई अन्तः बिन्दु O हो तो सिद्ध कीजिए कि
(BC+AB+AC)<(OA+OB+OC)
उपर्युक्त सवालों को हल करने पर त्रिभुज में असमिकाएं कक्षा 9 (Inequalities of Triangle in Class 9),त्रिभुज की असमिका का प्रमाण (Proof of Triangle Inequality) को ठीक से समझ सकते हैं।
Also Read This Article:-Some Properties of Triangle Class 9
4.त्रिभुज में असमिकाएं कक्षा 9 (Frequently Asked Questions Related to Inequalities of Triangle in Class 9),त्रिभुज की असमिका का प्रमाण (Proof of Triangle Inequality) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्नः
प्रश्न:1.एक त्रिभुज में असमिकाओं की मुख्य बातें लिखिए। (Write HIGHLIGHTS of Inequalities in a Triangle):
उत्तरः(1.)किसी त्रिभुज में लम्बी (बड़ी) भुजा का सम्मुख कोण बड़ा होता है। (2.)किसी त्रिभुज में बड़े कोण की सम्मुख भुजा लम्बी (बड़ी) होती है। (3.)किसी त्रिभुज में दो भुजाओं का योग तीसरी भुजा से बड़ा होता है। (4.)त्रिभुज का परिमाप उसकी माध्यिकाओं के योग से बड़ा होता है। (5.)त्रिभुज के तीन शीर्षलम्बों का योग उसके परिमाप से कम होता है। (6.)त्रिभुज की किन्हीं दो भुजाओं का अन्तर तीसरी भुजा से कम होता है।
प्रश्न:2.असमिका से क्या तात्पर्य है? (What Do You Mean by Inequations?):
उत्तरःसमीकरण के दोनों पक्ष बराबर होते हैं।यदि दोनों पक्ष बराबर नहीं हों तब मध्य में > (बड़ा), < (छोटा), \geq (बड़ा या बराबर), \leq (छोटा या बराबर) में से कोई चिन्ह लगाते हैं।इन्हें असमिकाएं कहते हैं।
प्रश्नः3.उत्तल बहुभुज किसे कहते हैं? (What is a Convex Polygon?):
उत्तरःवह बहुभुज जिसमें प्रत्येक कोण का माप दो समकोण से छोटा होता है,उत्तल बहुभुज कहलाता हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा त्रिभुज में असमिकाएं कक्षा 9 (Inequalities of Triangle in Class 9),त्रिभुज की असमिका का प्रमाण (Proof of Triangle Inequality) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Inequalities of Triangle in Class 9
त्रिभुज में असमिकाएं कक्षा 9
(Inequalities of Triangle in Class 9)
Inequalities of Triangle in Class 9
त्रिभुज में असमिकाएं कक्षा 9 (Inequalities of Triangle in Class 9) के इस आर्टिकल में किसी
त्रिभुज में असमान भुजाओं और असमान कोणों में सम्बन्ध का अध्ययन करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.