1.त्रिभुज की असमिकाएं कक्षा 9 (Inequalities of triangle class 9)-

त्रिभुज की असमिकाएं कक्षा 9 (Inequalities of triangle class 9) में हम अध्ययन करेंगे कि त्रिभुज की भुजाओं के माप बदलने पर उसके कोणों के माप भी बदल जाते हैं और यदि त्रिभुज के कोणों के माप बदलें तो भुजाओं के माप भी बदल जाते हैं।
(1.)त्रिभुज असमिका प्रमाण (Triangle inequality proof)-
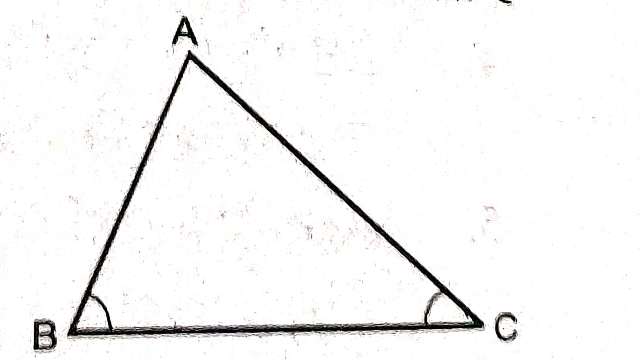
प्रमेय (Theorem):1.यदि किसी त्रिभुज की दो भुजाएं असमान हों तो बड़ी भुजा के सामने का कोण छोटी भुजा के सामने के कोण से बड़ा होता है।
दिया है (Given):त्रिभुज ABC में AB>AC
सिद्ध करना है (To Prove):\angle C> \angle B
रचना (Construction): शीर्ष C से CD इस प्रकार खींची कि AC=AD हो।

उपपत्ति (Proof):रचना से \triangle ACDमें भुजा AC=AD समान है। अतः इनके सम्मुख कोण भी समान होंगे।
अतः \angle ACD= \angle ADC……..(1)
\because  \angle ADC त्रिभुज BDC का बहिष्कोण है
अतः \angle ADC>\angle B………(2)
(1) व (2) से-

\angle ACD>\angle B…….(3)
चित्र से \angle ACB>\angle ACD…..(4)
(3) व (4) से-

\angle ACB>\angle ACD>\angle B \\ \Rightarrow  \angle ACB> \angle B
अर्थात् \angle C> \angle B
प्रमेय (Theorem):2.किसी त्रिभुज में बड़े कोण की सम्मुख भुजा छोटे कोण की सम्मुख भुजा से बड़ी होती है।
दिया है (Given):त्रिभुज ABC में \angle B> \angle C
सिद्ध करना है (TO Prove):AC>AB

उपपत्ति (Proof): \triangle ABC की भुजा AC एवं AB के लिए निम्नलिखित तीन संभावनाएं हो सकती हैं जिनमें से केवल एक ही संभव है:
(i)AC=AB
(ii)AC>AB
स्थिति (i) :जब AC=AB हो
यदि AC=AB हो तो में समान भुजाओं के सम्मुख कोण समान होंगे अर्थात् \angle B=\angle C जो कि असंभव है क्योंकि दिया हुआ है कि

\angle B >\angle C
अतः AC\neq AB

स्थिति (ii) :जब AC<AB हो
बड़ी भुजा के सामने का कोण बड़ा होता है।
अतः AC<AB \Rightarrow \angle C<\angle B

AC \nless AB
स्थिति (iii) :जब AC>AB हो
अब हमारे पास तीसरी संभावना शेष है जो अवश्य सत्य होगी
अर्थात् AC>AB 
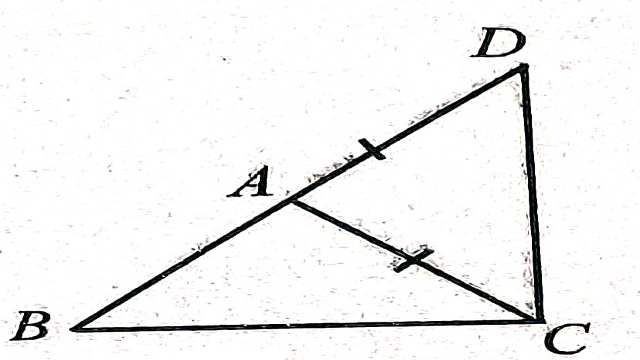
प्रमेय (Theorem):3. किसी त्रिभुज की दो भुजाओं का योग उसकी तीसरी भुजा से बड़ा होता है।
दिया है (Given):एक त्रिभुज ABC है।

सिद्ध करना है (To Prove):
(i)AB+BC>AC
(ii)BC+AC>AB
(iii)AC+AB>BC
रचना (Construction):भुजा BA को D तक इस प्रकार आगे बढ़ाया कि AD=AC हो।
उपपत्ति (Proof): \triangle ADC में रचना से AD=AC है अतः इनके सम्मुख कोण बराबर होंगे।
अतः \angle ACD=\angle ADC……(1)
एवं \angle BCD>\angle ACD…….(2)
(1) व (2) से-

\angle BCD>\angle ADC=\angle BDC
अतः BD>BC [क्योंकि बड़े कोण की सम्मुख भुजा बड़ी होती है।]
अतः BD>BC
BD+AD>BC [BD=BA+AD]
BA+AC>BC [AD=AC (रचना से)]
इसी प्रकार हम सिद्ध कर सकते हैं कि
AB+BC>AC
BC+AC>AB
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके ।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए ।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।

Also Read This Article:-Lines and Angles for Class 9

2.रेखा एवं बाह्य बिन्दु से लम्बवत दूरी (Vertical distance from line and outer point)-

किसी रेखा एवं उसके बाहर स्थित किसी बिन्दु के मध्य दूरी,उस बिन्दु से उस रेखा पर डाले गए लम्ब की लम्बाई के बराबर होती है।
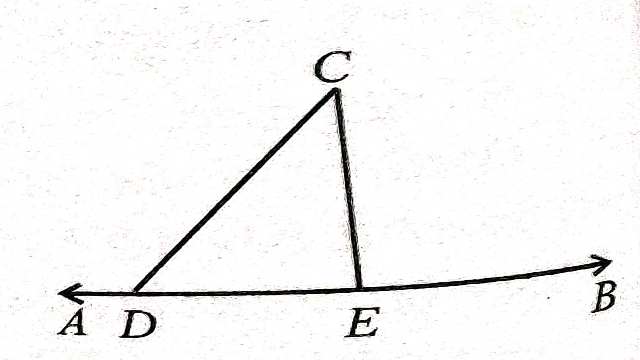
प्रमेय (Theorem):4.किसी बाह्य बिन्दु से सरल रेखा (रेखा खण्ड) पर खींचे गए सभी रेखाखण्डों में लम्बवत् रेखाखण्ड ही सबसे छोटा होता है।
दिया है (Given):रेखा AB पर बिन्दु C से रेखाखण्ड CD एवं लम्ब CE मिलाया।
सिद्ध करना है (To Prove):CE<AD

उपपत्ति (Proof): \triangle CED में

\angle CED=90°

अतः \angle CDE<\angle CED होगा,हम जानते हैं कि बड़े कोण की सम्मुख भुजा सदैव बड़ी होती है।अतः CD<CE 

अर्थात् बाह्य बिन्दु से खींचे गए रेखाखण्डों में से लम्बवत् रेखाखण्ड ही सबसे छोटा होता है।

3.त्रिभुज की असमिकाएं कक्षा 9 के उदाहरण (Inequalities of triangle class 9 Examples), त्रिभुज असमिका प्रमेय उदाहरण (Triangle inequality theorem examples)-

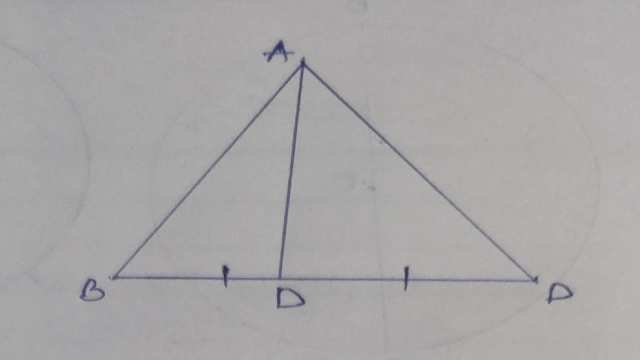
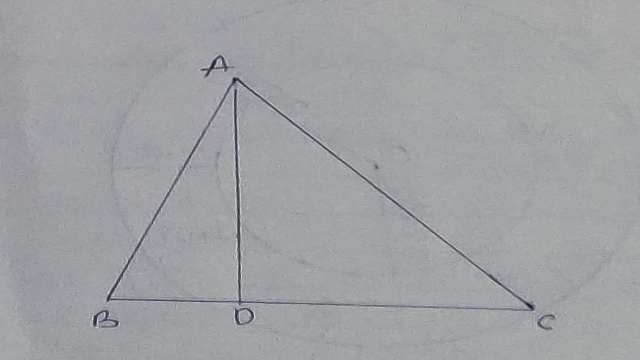
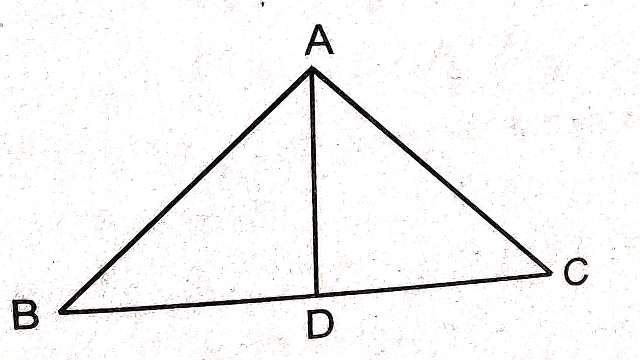
Example-1.सिद्ध कीजिए कि एक त्रिभुज की किन्हीं दो भुजाओं का योग तीसरी भुजा की संगत माध्यिका के दोगुने से बड़ा होता है।

Solution-दिया है (Given): \triangle ABC में AD माध्यिका है।

सिद्ध करना है (To Prove):AB+AC>2AD

उपपत्ति (Proof): \triangle ABD में

\triangle ADB>\triangle ABD

अतः AB>AD …..(1)

(बड़े कोण के सामने की भुजा बड़ी होती है।)

इसी प्रकार \triangle ACD में

AC>AD   ………..(2)
(बड़े कोण के सामने की भुजा बड़ी होती है।)
समीकरण (1) व (2) को जोड़ने पर-
AB+AC>2AD
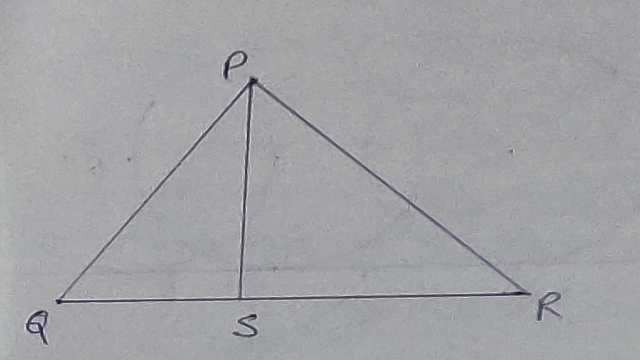
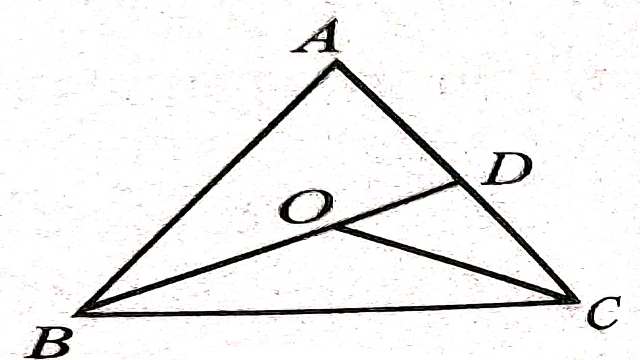
Example-2.\triangle PQR की भुजा QR पर कोई बिन्दु S स्थित है।दर्शाइए कि PQ+QR+RP>2 PS है।
Solution- दिया है (Given): \triangle PQR में QR पर S कोई बिन्दु है।
सिद्ध करना है (To Prove):PQ+QR+RP>2PS

उपपत्ति (Proof): \triangle PQS में
PQ+QS>PS …….(1)
(त्रिभुज की दो भुजाओं का योग तीसरी भुजा से अधिक होता है।)
इसी प्रकार \triangle PRS में
PR+RS>PS ……….(2)
(त्रिभुज की दो भुजाओं का योग तीसरी भुजा से बड़ा होता है।)
(1) व (2) का योग करने पर-
PQ+QS+PR+RS>PS+PS
\Rightarrow  PQ+(QS+PR)+RS>2 PS \\ \Rightarrow  PQ+QR+RS>2PS
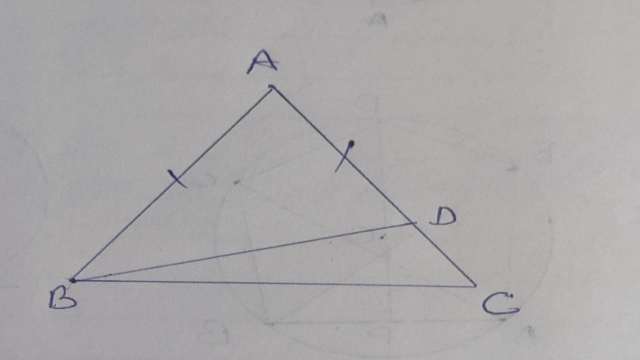
Example-3.AB=AC वाले एक \triangle ABC की भुजा ,AC पर D कोई बिन्दु स्थित है।दर्शाइए कि CD<BD

Solution- दिया हुआ है (Given):\triangle ABC में AB=AC तथा भुजा AC पर D कोई बिन्दु है।

सिद्ध करना है (To Prove):CD<BD 

उपपत्ति (Proof): \triangle ABC में AB=AC 

\angle ABC=\angle ACB(बराबर भुजा के अभिमुख कोण बराबर होते हैं।)……(1)

\angle ABC>\angle DBC….(2)

(1) व (2) से-

\angle ACB>\angle DBC

अतः BD>CD 

(बड़े कोण के सामने की भुजा बड़ी होती है।)

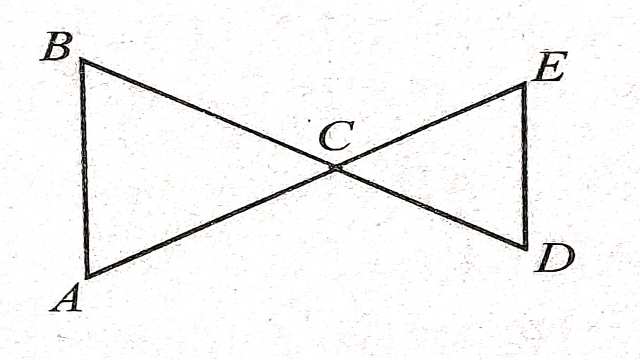
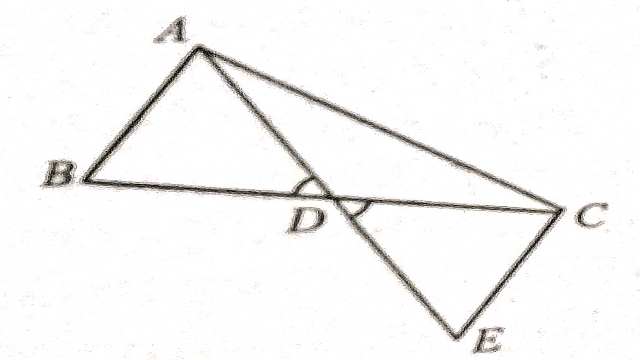
Example-4.चित्र में \angle B>\angle A एवं \angle D>\angle E हो तो सिद्ध कीजिए कि AE>BD
Solution- दिया है (Given):\angle B>\angle A एवं \angle D>\angle E
सिद्ध करना है (To Prove):AE>BD

उपपत्ति (Proof): \triangle ABC में

\angle B>\angle A
अतः AC>BC ……….(1)(बड़े कोण के सामने की भुजा बड़ी होती है।)
\triangle DCE में

\angle D>\angle E
अतः CE>CD…….(2) (बड़े कोण के सामने की भुजा बड़ी होती है।)
(1) व (2) को जोड़ने पर-
AC+CE>BC+CD
\Rightarrow  AE>BD
Example-5.किसी त्रिभुज ABC में AB>AC एवं भुजा BC पर कोई बिन्दु D हो तो सिद्ध कीजिए AB>AD.
Solution-दिया है (Given): \triangle ABC में AB>AC तथा BC पर कोई बिन्दु D है।
सिद्ध करना है (To Prove):AB>AD

उपपत्ति (Proof): \triangle ABC में
AB>AC ……(1)
अतः \angle ACD>\angle ABC (बड़ी भुजा के सामने का कोण बड़ा होता है।)…..(2)
\angle ADC>\angle ACD (AD,भुजा BC पर स्थित है।)……(3)
(2) व (3) से-

\angle ADB>\angle ABC
अतः AB>AD (बड़े कोण के सामने की भुजा बड़ी होती है।)
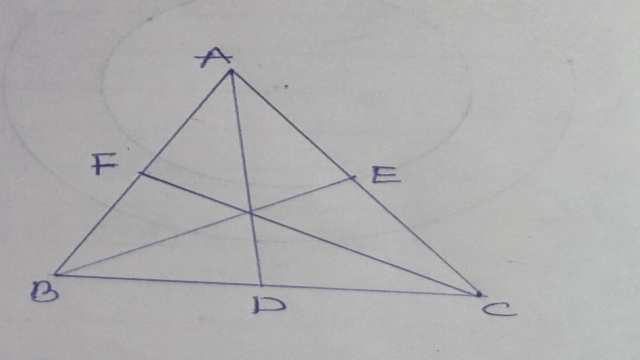
Example-6.सिद्ध कीजिए कि त्रिभुज की तीनों भुजाओं का योग उसकी तीनों माध्यिकाओं के योग से अधिक होता है।
Solution-दिया है (Given): \triangle ABC में AD,BE व CF माध्यिकाएं हैं।
सिद्ध करना है (To Prove):AB+BC+AC>AD+SE+CF

उपपत्ति (Proof): \triangle ABD में
चित्र से \angle ADB>\angle ABD
AB>AD ……..(1)
(बड़े कोण की सम्मुख भुजा बड़ी होती है।)
\triangle BCE में
चित्र से-\angle BEC>\angle ACB
BC>BE ……(2)
(बड़े कोण की सम्मुख भुजा बड़ी होती है।)
इसी प्रकार \triangle ACF में

\angle AFC>\angle CAF
AC>CF ……..(3)
(बड़े कोण की सम्मुख भुजा बड़ी होती है।)
(1),(2),(3) को जोड़ने पर-
AB+BC+AC>AD+BE-CF
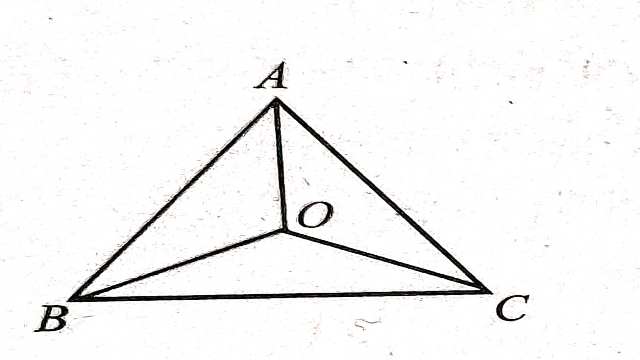
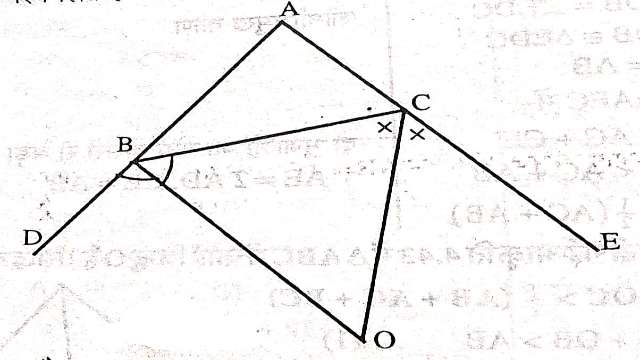
Example-7.चित्र में O कोई अन्त: बिन्दु है। सिद्ध कीजिए कि 

(BC+AB+AC)<2(OA+OB+OC)

Solution:-दिया है (Given): \triangle ABC में O कोई अन्त: बिन्दु है।
सिद्ध करना है (To Prove):(BC+AB+AC)<2(OA+OB+OC)

उपपत्ति (Proof): \triangle AOB में AO+OB>AB …….(1)
(त्रिभुज की दो भुजाओं का योग तीसरी भुजा से अधिक होता है।)
\triangle BOC में
BO+OC>BC …..(2)
(त्रिभुज की दो भुजाओं का योग तीसरी भुजा से अधिक होता है।)
इसी प्रकार \triangle AOC में
AO+OC>AC ……(3)
(त्रिभुज की दो भुजाओं का योग तीसरी भुजा से अधिक होता है।)
(1),(2),(3) का योग करने पर-
AO+OB+OB+OC+AO+OC>AB+BC+AC
\Rightarrow  2(AO+OB+OC)>AB+BC+AC
Example-8.चित्र में AD कोण BAC का समद्विभाजक है। सिद्ध कीजिए कि AB>BD है।
Solution-दिया है (Given):\triangle ABC में AD,\angle BAC का समद्विभाजक है।
सिद्ध करना है (To Prove):AB>BD

उपपत्ति (Poof):\angle ADB=\angle C+\angle DAC
(त्रिभुज का बहिष्कोण अन्तराभिमुख कोणों के योग के बराबर होता है।)……(1)
\angle BAD=\angle DAC(दिया है)……..(2)
(1) व (2) से-

\angle ADB=\angle C+\angle BAD \\ \Rightarrow \angle ADB>\angle BAD
AB>BD
(बड़े कोण की सम्मुख भुजा बड़ी होती है।)
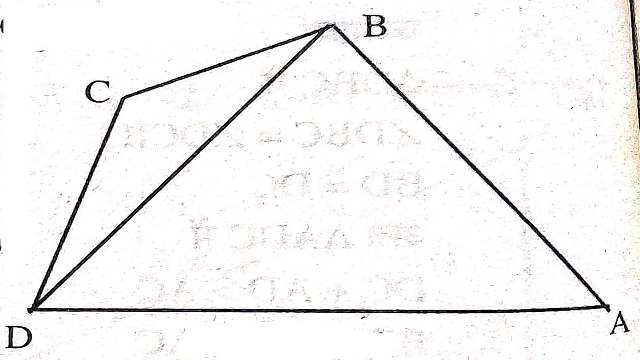
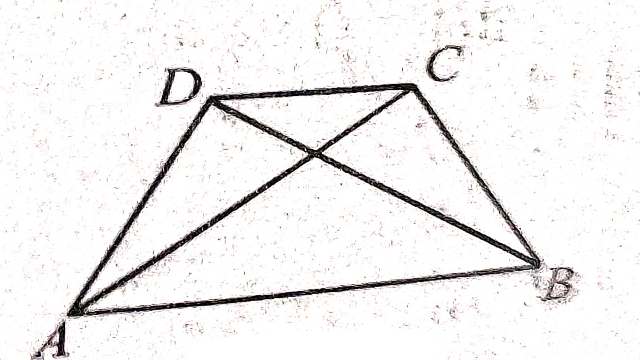
Example-9.ABCD एक चतुर्भुज है जिसमें भुजा AD सबसे बड़ी भुजा है तथा BC सबसे छोटी है। \angle ABC>\angle ADC

Solution:-दिया है (Given):ABCD एक चतुर्भुज है जिसमें भुजा AD सबसे बड़ी भुजा है तथा BC सबसे छोटी है।

सिद्ध करना है (To Prove):\angle ABC>\angle ADC
रचना (Construction):B,D को मिलाइए।

उपपत्ति (Proof): \triangle ABD में
AD>AB (दिया है)

\angle ABD>\angle ADB…..(1)
(बड़ी भुजा के सामने का कोण बड़ा होता है।)
\triangle BCD में
CD>BC
(BC सबसे छोटी भुजा है।)

\angle DBC>\angle CDB…..(2)
(बड़ी भुजा के सामने का कोण बड़ा होता है।
(1) व (2) को जोड़ने पर-

\angle ABD+\angle DBC>\angle ADB+\angle CDB \\ \Rightarrow \angle ABC> \angle ADC
Example-10.चित्र में \triangle ABC की भुजाएं AB व AC को क्रमशः D तथा E बिन्दु तक बढ़ाया गया है। \angle DBC तथा  \angle ECB के समद्विभाजक BO तथा CO बिन्दु O पर मिलते हैं।यदि AB>AC तो सिद्ध कीजिए कि OC>OB.
Solution-दिया है (Given): \angle DBC तथा \angle ECB  के समद्विभाजक BO तथा CO बिन्दु O पर मिलते हैं।AB>AC

सिद्ध करना है (To Prove):OC>OB

उपपत्ति (Proof):AB>AC (दिया है)

\angle ACB>\angle ABC……(1)
(बड़े कोण की सम्मुख भुजा बड़ी होती है।)
\angle ABC+\angle DBC=180 (रैखिक कोण-युग्म से)……(2)
\angle ACB+\angle ECB=180 (रैखिक कोण-युग्म से)……(3)
(2) व (3) से-

\angle ABC+\angle DBC=\angle ACB+\angle ECB
(1) व (4) से-

\angle DBC>\angle ECB \\ \frac{1}{2} \angle DBC>\frac{1}{2}  \angle ECB......(5) \\ \angle CBO=\angle OBD=\frac{1}{2} \angle DBC (दिया है)…….(6)
\angle ECO=\angle BCO =\frac{1}{2}  \angle BCE (दिया है)
(5),(6) व (7) से-

\angle CBO>\angle OCB
OC>BO
(बड़े कोण की सम्मुख भुजा बड़ी होती है।)
Example-11.सिद्ध कीजिए कि त्रिभुज के तीनों शीर्ष लम्बों का योग त्रिभुज के परिमाप से कम होता है।
Solution:-दिया है (Given):\triangle ABC में AD \perp BC ,BE \perp AC,CF \perp AB   
सिद्ध करना है (To Prove): मेंAB+BC+CA>AD+BE+CF

उपपत्ति (Proof): \triangle ABD में

\angle ADB>\angle ABC 
(त्रिभुज में समकोण अन्य कोण से बड़ा होता है।)
AB>AD ……….(1)
(बड़े कोण की सम्मुख भुजा बड़ी होती है।)
\triangle BEC में

\angle BEC>\angle BCE 
(त्रिभुज में समकोण अन्य कोण से बड़ा होता है।)
BC>BE ………..(2)
(बड़े कोण की सम्मुख भुजा बड़ी होती है।)

\triangle ACF में

\angle AFC>\angle CAF 
(त्रिभुज में समकोण अन्य कोण से बड़ा होता है।)
AC>CF ………..(3)
(बड़े कोण की सम्मुख भुजा बड़ी होती है।)
(1),(2) ,(3) को जोड़ने पर-
AB+BC+AC>AD+BE+CF
उपर्युक्त उदाहरणों के द्वारा त्रिभुज की असमिकाएं कक्षा 9 (Inequalities of triangle class 9) को समझ सकते हैं।

4.त्रिभुज की असमिकाएं कक्षा 9 समस्याएं (Inequalities of triangle class 9 Problems)-

(1.)चित्र में AD,त्रिभुज ABC की माध्यिका है तो सिद्ध कीजिए कि AB+AC>2AD

(2.) यदि ABCD एक चतुर्भुज है तो सिद्ध कीजिए कि
(i)AB+BC+CD+DA>2AC
(ii)AB+BC+CD+DA>AC+BD

(3.)चित्र में \triangle ABC के अन्दर कोई बिन्दु O हो तो सिद्ध कीजिए कि AB+AC>OB+OC

(4.)सिद्ध कीजिए कि किसी त्रिभुज की दो भुजाओं का अन्तर तीसरी भुजा से छोटा होता है।
उपर्युक्त सवालों को हल करने पर त्रिभुज की असमिकाएं कक्षा 9 (Inequalities of triangle class 9) को ठीक से समझ सकते हैं।

5.त्रिभुज असमिका प्रमेय प्रमाण (Triangle Inequality Theorem Proof)-

इसलिए,आइए देखें कि क्या दो भुजाओं का योग तीसरी भुजा से अधिक है।यदि नहीं तो इसलिए, त्रिभुज की भुजा असमानता के सिद्धांत को संतुष्ट नहीं करते हैं।

6.आप एक त्रिभुज की असमानता को कैसे ज्ञात करते हैं? (How do you find the inequality of a triangle?)-

त्रिभुज की असमिकाएँ
यदि एक त्रिभुज के दो भुजाएं असमान हैं,तो सबसे बड़ी भुजा का सम्मुख कोण दूसरों की कोणों की तुलना में अधिक होता है।इस बिंदु को साबित करने के लिए हमें एक गतिविधि करने की आवश्यकता है।
बड़े कोण की सम्मुख भुजा किसी भी त्रिभुज में सबसे बड़ी होती है।
त्रिभुज की किन्हीं दो भुजाओं का योग हमेशा तीसरी भुजा से अधिक होता है।

7.एक त्रिभुज में असमिकाएँ क्या हैं? (What are the inequalities in one triangle?)-

बड़ा कोण और बड़ी साइड प्रमेय बताता है कि एक त्रिभुज के भीतर, बड़ी भुजा बड़े कोण के विपरीत ओर स्थित होते हैं, और त्रिभुज असमानता प्रमेय में कहा गया है कि त्रिभुज के किसी भी दो भुजाओं का योग तीसरी भुजा से अधिक होना चाहिए।

8.कब त्रिभुज असमिका एक समानता है? (When triangle inequality is an equality?)-

यूक्लिडियन मामले में, समानता केवल तब होती है जब त्रिभुज में 180° कोण और दो 0° कोण होते हैं, जिससे तीन शीर्ष संरेख हैं, जैसा कि नीचे उदाहरण में दिखाया गया है।इस प्रकार, यूक्लिडियन ज्यामिति में, दो बिंदुओं के बीच सबसे छोटी दूरी एक सीधी रेखा है।
उपर्युक्त प्रश्नों के उत्तर द्वारा,उदाहरणों तथा सवालों को हल करके त्रिभुज की असमिकाएं कक्षा 9 (Inequalities of triangle class 9) को भली-भांति समझ सकते हैं।

Also Read This Article:-Congruence of Triangles

No.	Social Media	Url
1.	Facebook	click here
2.	you tube	click here
3.	Instagram	click here
4.	Linkedin	click here
5.	Facebook Page	click here