Important Examples on Lines and Angles
1.रेखाओं और कोण पर महत्त्वपूर्ण उदाहरण का परिचय (Introduction to Important Examples on Lines and Angles),रेखाओं और कोण पर आधारित महत्त्वपूर्ण उदाहरण (Important Examples Based on Lines and Angles):
रेखाओं और कोण पर महत्त्वपूर्ण उदाहरण (Important Examples on Lines and Angles) के इस आर्टिकल में समान्तर रेखाओं को काटने वाली तिर्यक रेखाओं और उनके द्वारा बनाए गए कोण पर आधारित सवाल हल करके समझने का प्रयास करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके । यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए । आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Questions of Algebraic Identity
2.रेखाओं और कोण पर महत्त्वपूर्ण उदाहरण (Important Examples on Lines and Angles):
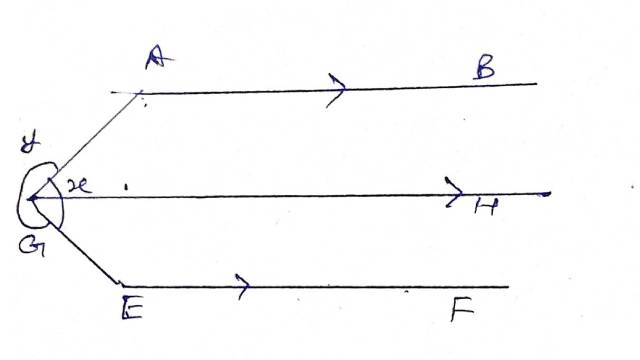
Example:1.चित्र में रेखाएँ AB,CD और EF परस्पर समान्तर हैं तो \angle x , \angle y , \angle z और \angle p ज्ञात कीजिए।
Solution: CD \| EF तथा FD तिर्यक रेखा इनको काटती है अतः \angle DFE+\angle CDF=180 (तिर्यक रेखा के एक ही ओर के अन्त:कोण)
\Rightarrow 58^{\circ}+\angle p=180^{\circ} \\ \Rightarrow \angle p=180^{\circ}-58^{\circ} \\ \Rightarrow \angle p=122^{\circ} \\ \angle D F E=\angle Z (संगत कोण)
\Rightarrow \angle Z=58^{\circ} \\ AB \| CD तथा तिर्यक रेखा FD इनको काटती है
\angle z+\angle y=180 (तिर्यक रेखा के एक ही ओर के अन्तःकोण)
\Rightarrow 58^{\circ}+\angle y=180^{\circ} \\ \Rightarrow \angle y=180^{\circ}-58^{\circ} \\ \angle y=122^{\circ} \\ \angle z=\angle x (एकान्तर कोण)
\Rightarrow \angle x=58^{\circ} \\ \Rightarrow \angle x=58^{\circ}, \angle y=122^{\circ}, \angle z=58^{\circ}, \angle p=122^{\circ}
Example:2.चित्र में AB \| EF हैं। \angle x एवं \angle y ज्ञात कीजिए।
Solution: AB \|EF \| GH रेखा खींची।
AB \| GH तथा तिर्यक रेखा AG इनको काटती है
\angle BAG+\angle AGH=180^{\circ} (तिर्यक रेखा के एक ही ओर के अन्तःकोण)
125^{\circ}+\angle A G H=80^{\circ} \\ \Rightarrow \angle A G H=180^{\circ}-125^{\circ} \\ \Rightarrow \angle A G H=55^{\circ}
इसी प्रकार AB \| EF तथा GE तिर्यक रेखा इनको काटती है।
\angle HGE+ \angle GEF=180^{\circ} (तिर्यक रेखा के एक ही ओर के अन्तःकोण)
\Rightarrow \angle HGE+141^{\circ}=180^{\circ} \\ \Rightarrow \angle HGE=180^{\circ} -141^{\circ} \\ \Rightarrow \angle HGE=39^{\circ} \\ \angle AGH+\angle HGE= 55^{\circ}+39^{\circ} \\ \Rightarrow \angle X=94^{\circ} \\ \angle x+\angle y=360^{\circ} (एक ही बिन्दु पर बने कोण)
\Rightarrow 94^{\circ}+\angle y=360^{\circ} \\ \Rightarrow \angle y=360^{\circ}-94^{\circ} \\ \Rightarrow \angle y=266^{\circ} \\ \angle x=94^{\circ}, \angle y=266^{\circ}
Example:3.चित्र में l \| m तो \angle 1 के तुल्य कोणों को बताइए।
Solution: \angle 1=\angle 3 (शीर्षाभिमुख कोण)
l \| m
अतः \angle 3 =\angle 7 (संगत कोण)
\angle 1 =\angle 5 (संगत कोण)
\angle 5 =\angle 7 (शीर्षाभिमुख कोण)
अतः \angle 1=\angle 3=\angle 5=\angle 7
Example:4.चित्र में \angle 1=60^{\circ} और \angle 6=120^{\circ} है।दर्शाइए कि m और n समान्तर हैं।
Solution: \angle 1=\angle 3(शीर्षाभिमुख कोण)
\angle 3=60^{\circ} \\ \angle 3+\angle 6=60^{\circ}+120^{\circ} \\ \Rightarrow \angle 3+\angle 6=180^{\circ} \\ \angle 3 व \angle 6 तिर्यक रेखा के एक ही ओर के अन्तःकोण हैं अतः m \| n
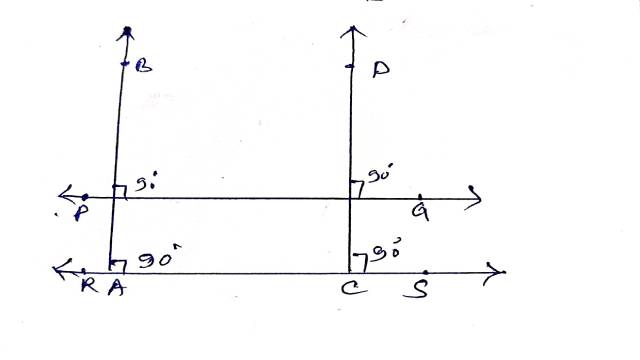
Example:5.दो सरल रेखाएँ क्रमशः दो समान्तर रेखाओं पर लम्ब हैं।दर्शाइए कि ये दोनों सरल रेखाएँ परस्पर समान्तर हैं।
Solution:दिया है (Given): PQ\|RS तथा AB \perp PQ , AB \perp RS , CD \perp PQ व CD \perp RS
सिद्ध करना है (To Prove): AB \| CD
उपपत्ति (Proof): \angle BAE+\angle DCA=180^{\circ}
(ये तिर्यक रेखा RS के एक ही ओर के अन्तःकोण हैं)
अतः AB \| CD
Example:6.चित्र में POQ एक सरल रेखा है।x का मान है:
Solution: 40^{\circ}+4 x+3 x=180^{\circ} (रैखिक कोण अभीगृहीत से)
\Rightarrow 7 x=180^{\circ}-40^{\circ} \\ \Rightarrow 7 x=140^{\circ} \\ \Rightarrow x=\frac{140^{\circ}}{7}=20^{\circ}
Example:7.चित्र में OP \| RS , \angle OPQ=110^{\circ} और \angle QRS=130^{\circ} है तो \angle PQR बराबर है
Solution: OP \| RS \| QT रेखा खींची
OT \| RS तथा तिर्यक रेखा QR इनको काटती है।
\angle SRQ+\angle RQT=180^{\circ} (तिर्यक रेखा के एक ही ओर के अन्तःकोण)
130^{\circ}+\angle R Q T=180^{\circ} \\ \Rightarrow \angle R Q T=180^{\circ}-130^{\circ} \\ \Rightarrow \angle RQT=50^{\circ} \cdots(1) \\ OP \| QT
तथा तिर्यक रेखा PQ इनको काटती है
\angle OPQ=\angle PQT (एकान्तर कोण)
\angle PQT=110^{\circ} \cdots(2) \\ \angle PQT=\angle P Q R+\angle R Q T \\ \Rightarrow 110^{\circ}=\angle PQR+50^{\circ} \\ \Rightarrow \angle P Q R=110^{\circ}-50^{\circ} \\ \Rightarrow \angle PQR=60^{\circ}
Example:8.चित्र में वृहत कोण, \angle AOB बराबर है:
Solution: \angle AOB +वृहत कोण \angle AOB=360^{\circ}
(एक बिन्दु पर बने कोणों का योग)
\Rightarrow 60^{\circ}+ वृहत कोण \angle AOB=360^{\circ} \\ \Rightarrow वृहत कोण \angle AOB=300^{\circ}
Example:9.चित्र से बताइए कि निम्न में कौनसा कोण युग्म संगत कोण है:
(A)\angle 1, \angle 5 (B) \angle 2, \angle 6 (C)\angle 3, \angle 7 (D) \angle 3, \angle 6
Solution:विकल्प (D) सही है।
Example:10.चित्र में दो समान्तर रेखाएँ l तथा m को एक तिर्यक रेखा n,बिन्दुओं G तथा H पर काट रही है,इस प्रकार बनने वाले कोण चित्र में अंकित है।
यदि \angle 1 न्यून कोण हो तो बताइए निम्न में कौनसा कथन असत्य है:
(A) \angle 1+\angle 2=180^{\circ}
(B) \angle 2+\angle 5=180^{\circ}
(C) \angle 3 + \angle 8=180^{\circ}
(D) \angle 2+\angle 6=180^{\circ}
Solution:विकल्प (D) असत्य है।
उपर्युक्त उदाहरणों के द्वारा रेखाओं और कोण पर महत्त्वपूर्ण उदाहरण (Important Examples on Lines and Angles),रेखाओं और कोण पर आधारित महत्त्वपूर्ण उदाहरण (Important Examples Based on Lines and Angles) को समझ सकते हैं।
3.रेखाओं और कोण पर महत्त्वपूर्ण उदाहरण पर आधारित सवाल (Questions Based on Important Examples on Lines and Angles):
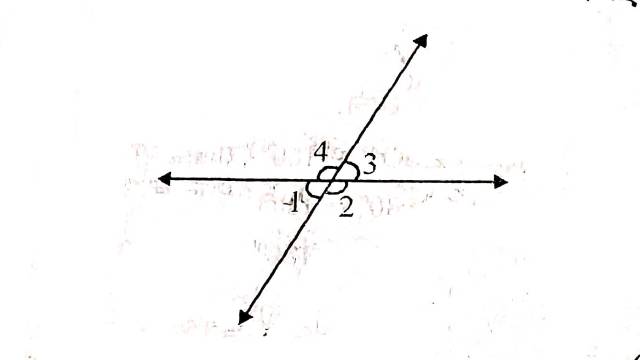
(1.)दी गई आकृति में दो सरल रेखाएँ एक-दूसरे को प्रतिच्छेद कर रही हैं।अंकित कोणों में \angle 1+\angle 2+\angle 3=230^{\circ} हो तो \angle 1 और \angle 4 ज्ञात कीजिए।
(2.)यदि AB,EF और CD तीन समान्तर रेखाएँ हों तथा \angle BAO=35^{\circ} और \angle AOC=90^{\circ} हो तो \angle OCD का मान ज्ञात कीजिए।
उत्तर (Answers): (1.) \angle 1=50^{\circ}, \angle 4=130^{\circ} (2) \angle OCD=55^{\circ}
उपर्युक्त सवालों को हल करने पर रेखाओं और कोण पर महत्त्वपूर्ण उदाहरण (Important Examples on Lines and Angles),रेखाओं और कोण पर आधारित महत्त्वपूर्ण उदाहरण (Important Examples Based on Lines and Angles) को ठीक से समझ सकते हैं।
Also Read This Article:- Linear Equations in Two Variables 9th
4.रेखाओं और कोण पर महत्त्वपूर्ण उदाहरण (Frequently Asked Questions Related to Important Examples on Lines and Angles),रेखाओं और कोण पर आधारित महत्त्वपूर्ण उदाहरण (Important Examples Based on Lines and Angles) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.प्रमेय किसे कहते हैं? (What is Theorem?):
उत्तर:निगमनिक तर्क विधि द्वारा सत्यापित नियमों (निष्कर्षों) को प्रमेय कहते हैं।ज्यामिति में प्रमेय को सिद्ध करने के लिए विभिन्न चरणों का प्रयोग किया जाता है।
प्रश्न:2.उपप्रमेय किसे कहते हैं? (What is Corollary?):
उत्तर:प्रमेय को सिद्ध करने के उपरान्त कुछ ऐसे परिणाम प्राप्त होते हैं,जिन्हें सरलतापूर्वक समझा जा सकता है उपप्रमेय कहलाते हैं।
प्रश्न:3.निर्मेय किसे कहते हैं? (What is Called Construction?):
उत्तर:ज्यामितीय नियमों का उपयोग कर दी गई ज्यामितीय रचना को निर्मेय कहते हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा रेखाओं और कोण पर महत्त्वपूर्ण उदाहरण (Important Examples on Lines and Angles),रेखाओं और कोण पर आधारित महत्त्वपूर्ण उदाहरण (Important Examples Based on Lines and Angles) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Important Examples on Lines and Angles
रेखाओं और कोण पर महत्त्वपूर्ण उदाहरण
(Important Examples on Lines and Angles)
Important Examples on Lines and Angles
रेखाओं और कोण पर महत्त्वपूर्ण उदाहरण (Important Examples on Lines and Angles)
के इस आर्टिकल में समान्तर रेखाओं को काटने वाली तिर्यक रेखाओं और उनके द्वारा बनाए
गए कोण पर आधारित सवाल हल करके समझने का प्रयास करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.