Important Examples of Transformations
1.रूपान्तरण के महत्त्वपूर्ण उदाहरण का परिचय (Introduction to Important Examples of Transformations),सम्मिश्र विश्लेषण में रूपान्तरण (Transformations in Complex Analysis):
रूपान्तरण के महत्त्वपूर्ण उदाहरण (Important Examples of Transformations) के इस आर्टिकल में अनुकोण तथा तुल्यकोणी प्रतिचित्रण पर आधारित सवालों को हल करके समझने का प्रयास करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Uniform Convergence and Power Series
2.रूपान्तरण के महत्त्वपूर्ण उदाहरण (Important Examples of Transformations):
Example:1.दर्शाइए कि वृत्त |z-c|=R के सापेक्ष एक बिंदु a का व्युत्क्रम बिंदु c+\frac{R^2}{\bar{a}-\bar{c}} है।
(Show that the inverse of a point a with respect to the circle |z-c|=R is the point c+\frac{R^2}{\bar{a}-\bar{c}} .)
Solution:माना वृत्त की त्रिज्या R तथा केन्द्र C(c) है।यह भी माना कि वृत्त के सापेक्ष A(a) का व्युत्क्रम बिन्दु B(b) है।
तब बिन्दु C,A,B संरेख है अतः
\arg (b-c)=\arg (a-c) \\ =-\arg (\bar{a}-\bar{c}) \\ \left[\because \arg z=-\arg \bar{z}\right] \\ \Rightarrow \arg (b-c) + \arg (\bar{a}-\bar{c})=0 \\ \Rightarrow \arg (b-c)(\bar{a}-\bar{c})=0 \left[\because \arg z_1 z_2=\arg z_1+ \arg z_2\right] \\ \Rightarrow(b-c)(\bar{a}-\bar{c})[एक धनात्मक वास्तविक संख्या है]
वृत्त के सापेक्ष A व B व्युत्क्रम बिन्दु है।
CA \cdot CB=R^2 \\ \Rightarrow|a-c||b-c|=R^2 \\ \Rightarrow |\bar{a}-\bar{c}||b-c|=R^2 \\ \Rightarrow|(\bar{a}-\bar{c})(b-c)|=R^2 \\ \Rightarrow(\bar{a}-\bar{c})(b-c)=R^2,[\because (\bar{a}-\bar{c})(b-c) एक धनात्मक वास्तविक संख्या है]
\Rightarrow b-c=\frac{R^2}{\bar{a}-\bar{c}} \\ \Rightarrow b=c+\frac{R^2}{\bar{a}-\bar{c}}
Example:2.एक आयताकार डोमेन R को x=0,y=0,x=1,y=1 से घिरा हुआ मान लें।w-तल के क्षेत्र R’ का निर्धारण करें जिसमें रूपान्तरण w=z+(1-2i) के अंतर्गत R को मैप किया गया है।
(Let a rectangular domain R be bounded by x=0,y=0,x=1,y=1.Determine the region R’ of w-plane into which R is mapped under the transformation w=z+(1-2i))
Solution:w=z+(1-2i)
\Rightarrow u+iv=(x+iy)+(1-2i)
\Rightarrow u=x+1,v=y-2
प्रतिचित्रण u=x+1,रेखाएँ x=0,x=2 रेखाओं u=1,u=3 में प्रतिचित्रित होती हैं।
प्रतिचित्रण v=y-2,रेखाएँ y=0,y=1 प्रतिचित्रित होती हैं v=-2,v=-1 में।
अभीष्ट प्रतिचित्रण R’ आयताकार है जो u=1,u=3,v=-2,v=-1 से w-समतल में परिबद्ध है।
इसी प्रकार हम सिद्ध कर सकते हैं कि R का प्रत्येक बिन्दु,R’ के एक और केवल एक बिन्दु में प्रतिचित्रित किया जा सकता है और विलोमतः भी।अतः रूपान्तरण एक आयताकार रूपान्तरण को पूरा करता है।दिया हुआ प्रतिचित्रण w=z+\beta ,जहाँ \beta=1-2i प्रकार का है।यहाँ आयत R के परिवर्तन की सदिश दिशा है।
Example:3.रूपान्तरण w=e^{\frac{i \pi}{4}} z पर विचार करें और z-समतल में x=0,y=0 और x+y=1 रेखाओं से घिरे त्रिभुजाकार क्षेत्र के संगत w-तल में क्षेत्र का निर्धारण करें।
(Cosider the transformation w=e^{\frac{i \pi}{4}} z and determine the region in the w-plane corresponding to the triangular region bounded by the lines x=0,y=0 and x+y=1 in the z-plane.)
Solution: w=e^{\frac{i \pi}{4}} z\\ \Rightarrow u+i v=e^{\frac{i \pi}{4}}(x+i y) \\ \Rightarrow u+i v=\frac{1}{\sqrt{2}}(1+i) \cdot(x+i y) \\ =\frac{1}{\sqrt{2}} \left[ (x-y)+i(x+y) \right] \\ =\frac{1}{\sqrt{2}}(1+i) \cdot(x+i y)\\ \therefore u=\frac{1}{\sqrt{2}}(x-y) तथा v=\frac{1}{\sqrt{2}}(x+y)
जब x=0, u=\frac{1}{\sqrt{2}} y, v=\frac{1}{\sqrt{2}} y
अतः रेखा x=0,v=u में प्रतिचित्रित होती है।
जब y=0, u=\frac{1}{\sqrt{2}} x, v=\frac{1}{\sqrt{2}} x
इस प्रकार y=0,y=u में प्रतिचित्रित होती है।
रेखा x+y=1,v=\frac{1}{\sqrt{2}} में प्रतिचित्रित होती है।
अतः दिया हुआ z-समतल में त्रिभुजाकार क्षेत्र में v=u,v=-u तथा v=\frac{1}{\sqrt{2}} द्वारा प्रतिचित्रित होता है।दोनों क्षेत्रों के चित्र दिखाए गए हैं।
Example:4.रूपान्तरण w=2z पर विचार करें और w-समतल के क्षेत्र D’ का निर्धारण करें जिसमें z-समतल में x=0,y=0,x+y=1 रेखाओं से घिरा त्रिकोणीय क्षेत्र D इस परिवर्तन के अंतर्गत मैप किया गया है।
(Cosider the transformation w=2z and determine the region D’ of the w-plane into which the triangular region D enclosed by the lines x=0,y=0,x+y=1 in the z-plane is mapped under this transformation.)
Solution:w=2z
\Rightarrow u+iv=2(x+iy)=2x+i2y
\Rightarrow u=2x,v=2y
अतः रेखाएँ x=0,y=0 तथा x+y=1 क्रमशः u=0,v=0 तथा u+v=2 रेखाओं में रूपान्तरित होती है।इसके दोनों क्षेत्र चित्र में दिखाएं गए हैं।
Example:5.z-समतल में आयताकार क्षेत्र D को x=0,y=0,x=2,y=3 से घिरा हुआ मान लें।w-समतल के क्षेत्र D’ का निर्धारण करें जिसमें रूपान्तरण w=\sqrt{2} e^{\frac{i \pi}{4}} z के अंतर्गत D को प्रतिचित्रित किया गया है।
(Let the rectangular region D in the z-plane be bounded by x=0,y=0,x=2,y=3.Determine the region D’ of the w-plane into which D is mapped under the transformation w=\sqrt{2} e^{\frac{i \pi}{4}} z .)
Solution: w=\sqrt{2} e^{\frac{i \pi}{4}} z \\ \Rightarrow u+i v =\sqrt{2}\left(\cos \frac{\pi}{4}+i \sin \frac{\pi}{4}\right)(x+i y) \\ =(1+i)(x+i y) \\ =(x-y)+i(x+y) \\ \Rightarrow u=x-y तथा v=x+y
तब रेखा x=0 प्रतिचित्रित होती है u=-y,v=y अर्थात् v=-u
रेखा y=0 प्रतिचित्रित होती है u=x, v=x अर्थात् v=u
रेखा x=2 प्रतिचित्रित होती है u=2-y,v=2+y अर्थात् v+u=4
रेखा y=3 प्रतिचित्रित होती है u=x-3,v=x+3 अर्थात् v-u=6 दोनों क्षेत्र चित्र में दर्शाए गए हैं।
अतः दिया हुआ रूपान्तरण 45° कोण से वामावर्त घूमता है।
Example:6.रूपान्तरण w=\frac{1}{2} के अंतर्गत अनंत पट्टियों
(i) \frac{1}{4}<y<\frac{1}{2} (ii) 0<y<\frac{1}{2}
का चित्र ज्ञात करें।क्षेत्रों को ग्राफ़िक रूप से दिखाएँ।
(Find the images of the infinite strips
(i) \frac{1}{4}<y<\frac{1}{2} (ii) 0<y<\frac{1}{2}
under the transformation.Show the regions graphically.)
Solution: w=\frac{1}{2} \\ u+i v=\frac{1}{x+i y} \\ =\frac{x-i y}{x^2+y^2} \\ \Rightarrow u=\frac{x}{x^2+y^2}, v=\frac{-y}{x^2+y^2} \\ \Rightarrow \frac{u}{v}=-\frac{x}{y} \Rightarrow x=-\frac{u y}{v} \\ v=-\frac{y}{\frac{u^2 y^2}{v^2}+y^2}=-\frac{v^2}{\left(v^2+v^2\right) y} \\ \Rightarrow -\frac{v}{\left(u^2+v^2\right)}=y
(i) यदि y=\frac{1}{4} तब -\frac{v}{u^2+v^2}=\frac{1}{4} \\ \Rightarrow u^2+v^2+u v=0 \\ \Rightarrow u^2+(v+2)^2=4
अतः रेखा y=\frac{1}{4} वृत्त u^2+(v+2)^2=4 में प्रतिचित्रित होती है।
यदि y=\frac{1}{2} तब -\frac{v}{u^2+v^2}=\frac{1}{2} \\ u^2+(v+1)^2=1
अतः रेखा y=\frac{1}{2} ,वृत्त u^2+(v+1)^2=1 में प्रतिचित्रित होती है।
अतः z-समतल में अनन्त पट्टी \frac{1}{4}<y<\frac{1}{2}, वृत्तों u^2+(v+2)^2=u तथा u^2+(v+1)^2=1 ,w समतल के उभयनिष्ठ क्षेत्र में प्रतिचित्रित होती है।दोनों क्षेत्रों को चित्रों में दर्शाया गया है।
(ii)यदि y=0,v=0 तथा यदि y>0,v>0
ऊपर चित्र में रेखा y=\frac{1}{2} वृत्त u^2+(v+1)^2=1 में प्रतिचित्रित होती हैं।अतः y, \frac{1}{2} से 0 तक कम होता जाता है तो वृत्त बड़ा होता जाता है।
इसी प्रकार w-समतल अनन्त पट्टी 0<y<\frac{1}{2} अर्द्ध नीचे w-समतल में वृत्त u^2+(v+1)^2=1 के बाहर क्षेत्र में प्रतिचित्रित होती है।दोनों क्षेत्रों को चित्र में दर्शाया गया है।
Example: 7. सिद्ध करो कि w=i z कोण \frac{\pi}{2} के माध्यम से समतल में घूमता है। अनंत पट्टी 0 < x <1 की चित्र ज्ञात करें। (show that the transformation w=iz is a rotation of the z-plane through the angle \frac{\pi}{2}. Find the image of the infinite strip 0 < x <1.)
Solution:- w=i z\\ |w|=|i z| \\ =|i||z| \\ \Rightarrow|w|=|z|
तथा \arg w=\arg (i z) \\ =\arg i+\arg z \\ =\frac{\pi}{2}+\arg z
अत: रूपांतरण w = iz z-समतल मूलबिन्दु के सापेम कोण से धूमता है।
माना w = u + iv
\Rightarrow u+i v=i(x+i y) \\ =i x-y \\ \Rightarrow u=-y तथा v=x
इस प्रकार z-समतल में 0 < x <1 क्षेत्र w-समतल में क्षेत्र 0 < v <1 में प्रतिचित्रित होता है अर्थात अनन्त पट्टी काल्पनिक अक्ष के समान्तर x=0 तथा x=1 , समतल में, W-समतल में अनन्त पट्टी v=0 तथा v=1 वास्तविक अक्ष के समान्तर प्रतिचित्रित होता है
Example:8.सिद्ध करो कि रूपान्तरण w=iz+i कोण के माध्यम से z-समतल घूमता है।अनंत पट्टी x>0 को अर्धतल v>1 पर मैप करता है।
(Show that w=iz+i maps half plane x>0 onto half plane v>1.)
Solution:w=iz+i
\Rightarrow i+i v=i(x+i y)+i \\ \Rightarrow \left. \begin{array}{l} u=-y \\ v=x+1 \end{array}\right\} \Rightarrow x=v-1
अब x >0 \Rightarrow v-1 >0 \Rightarrow v>1
यही अभीष्ट परिणाम है।
उपर्युक्त उदाहरणों द्वारा रूपान्तरण के महत्त्वपूर्ण उदाहरण (Important Examples of Transformations),सम्मिश्र विश्लेषण में रूपान्तरण (Transformations in Complex Analysis) को समझ सकते हैं।
Also Read This Article:- Analytic Functions by Milne Thomson
3.रूपान्तरण के महत्त्वपूर्ण उदाहरण (Frequently Asked Questions Related to Important Examples of Transformations),सम्मिश्र विश्लेषण में रूपान्तरण (Transformations in Complex Analysis) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.रूपान्तरण या प्रतिचित्रण से क्या आशय है? (What Do You Mean by Transformation or Mapping?)
उत्तर:z-समतल एवं w-समतल के बिन्दुओं के मध्य समीकरणों w=f(z)=u+iv जहाँ u=u(x,y) तथा v=v(x,y) से परिभाषित संगति को प्रतिचित्रण या रूपान्तरण कहते हैं तथा इन दो समतलों में संगत बिन्दुओं के समुच्चय को एक-दूसरे का प्रतिबिम्ब (image) कहते हैं।
प्रश्न:2.अनुकोण प्रतिचित्रण से क्या आशय है? (What Do You Mean by Conformal Mapping?):
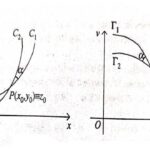
उत्तर:यदि रूपान्तरण इस प्रकार है कि वक्र C_1 तथा C_2के मध्य का कोण पर तथा वक्र \Gamma_1 तथा \Gamma_2 के मध्य कोण पर समान है।साथ में यदि दोनों समतलों पर दोनों चित्रों में कोण की एक अभिदिशा है तब ऐसे रूपान्तरण अथवा प्रतिचित्रण को अनुकोण प्रतिचित्रण कहते हैं।
प्रश्न:3.तुल्यकोणी प्रतिचित्रण से क्या आशय है? (What Do You Mean by Isogonal Mapping?):
उत्तर:यदि प्रतिचित्रण इस प्रकार है कि वक्रों के प्रतिच्छेदन बिन्दुओं पर कोणों का परिमाण अपरिवर्तित रहता है,परन्तु उनकी अभिदिशा बदल जाती है तो ऐसे प्रतिचित्रण को तुल्यकोणी (Isogonal) कहते हैं।
उपर्युक्त प्रश्नों के उत्तर द्वारा रूपान्तरण के महत्त्वपूर्ण उदाहरण (Important Examples of Transformations),सम्मिश्र विश्लेषण में रूपान्तरण (Transformations in Complex Analysis) के बारे में और अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Important Examples of Transformations
रूपान्तरण के महत्त्वपूर्ण उदाहरण
(Important Examples of Transformations)
Important Examples of Transformations
रूपान्तरण के महत्त्वपूर्ण उदाहरण (Important Examples of Transformations) के इस आर्टिकल
में अनुकोण तथा तुल्यकोणी प्रतिचित्रण पर आधारित सवालों को हल करके समझने का प्रयास करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.