Imp Examples of Surface Area of Cone
1.शंकु का पृष्ठीय क्षेत्रफल के महत्त्वपूर्ण उदाहरण का परिचय (Introduction to Imp Examples of Surface Area of Cone),शंकु का पृष्ठीय क्षेत्रफल कक्षा 9 (Surface Area of Cone Class 9):
शंकु का पृष्ठीय क्षेत्रफल के महत्त्वपूर्ण उदाहरण (Imp Examples of Surface Area of Cone) के इस आर्टिकल में शंकु पर आधारित कुछ विशिष्ट सवालों में पृष्ठीय क्षेत्रफल ज्ञात करके समझने का प्रयास करेंगे।
आपको यह जानकारी रोचक व ज्ञानवर्धक लगे तो अपने मित्रों के साथ इस गणित के आर्टिकल को शेयर करें।यदि आप इस वेबसाइट पर पहली बार आए हैं तो वेबसाइट को फॉलो करें और ईमेल सब्सक्रिप्शन को भी फॉलो करें।जिससे नए आर्टिकल का नोटिफिकेशन आपको मिल सके।यदि आर्टिकल पसन्द आए तो अपने मित्रों के साथ शेयर और लाईक करें जिससे वे भी लाभ उठाए।आपकी कोई समस्या हो या कोई सुझाव देना चाहते हैं तो कमेंट करके बताएं।इस आर्टिकल को पूरा पढ़ें।
Also Read This Article:- Important Examples of Surface Area
2.शंकु का पृष्ठीय क्षेत्रफल के महत्त्वपूर्ण उदाहरण (Imp Examples of Surface Area of Cone):
Example:1.यदि शंकु के आधार की त्रिज्या 21सेमी तथा ऊँचाई 28 सेमी हो,तो शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
Solution:शंकु के आधार की त्रिज्या (r)=21 सेमी
तथा ऊँचाई (h)=28 सेमी
शंकु की तिर्यक ऊँचाई l=\sqrt{h^2+r^2} \\ =\sqrt{(28)^2+(21)^2} \\ =\sqrt{784+441} \\ =\sqrt{7225} \\ \Rightarrow l =35 सेमी
अतः शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल=\pi r(l+r) \\ =\frac{22}{7} \times 21 \times(35+21) \\ =22 \times 3 \times 56 \\ =3696 वर्गसेमी
Example:2.एक टेन्ट शंकु के आकार का है।जिसके आधार की त्रिज्या 7 मीटर तथा ऊँचाई 5 मीटर है।टेन्ट में लगने वाले कपड़े का क्षेत्रफल ज्ञात कीजिए।
Solution:टेन्ट के आधार की त्रिज्या (r)=7 मीटर
तथा ऊँचाई (h)=5 मीटर
टेन्ट की तिर्यक ऊँचाई (l)=\sqrt{h^2+r^2} \\ =\sqrt{(5)^2+(7)^2} \\ =\sqrt{25+49} \\ =\sqrt{74} \\ =8.602 \\ l \approx 8.6 मीटर (लगभग)
अतः टेन्ट में लगने वाले कपड़े का क्षेत्रफल =\pi r l \\ =\frac{22}{7} \times 7 \times 8.6 \\ =\frac{1324.4}{7} \\ =189.2 वर्गमीटर
Example:3.एक शंकु के आधार का व्यास 12 मीटर और तिर्यक ऊँचाई 10 मीटर है।शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
Solution:शंकु के आधार की त्रिज्या (r)=\frac{12}{2} मीटर=6 मीटर
तथा तिर्यक ऊँचाई (l)=10 मीटर
शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल=\pi r(l+r) \\ =\frac{22}{7} \times 6 \times(10+6) \\ =\frac{22}{7} \times 6 \times 16 \\ =\frac{2112}{7} \text { वर्ग मीटर } \\ =301.714 \\ \approx 301.71 वर्गमीटर (लगभग)
Example:4.यदि एक शंकु का वक्रपृष्ठ 2035 वर्गसेमी और आधार का व्यास 35 सेमी हो,तो शंकु की तिर्यक ऊँचाई ज्ञात कीजिए।
Solution:शंकु के आधार की त्रिज्या (r)=\frac{35}{2}=17.5 सेमी
शंकु का वक्रपृष्ठ का क्षेत्रफल=\pi r l=2035 \\ \Rightarrow \frac{22}{7} \times \frac{35}{2} \times l=2035 \\ \Rightarrow l=\frac{2035 \times 7 \times 2}{22 \times 35} \\ =\frac{28490}{770} \\ \Rightarrow l=37 सेमी
Example:5.दो शंकुओं के आधार का व्यास समान है। उनकी तिर्यक ऊँचाइयों का अनुपात 5:4 है।यदि छोटे शंकु का वक्रपृष्ठ 400 वर्गसेमी हो,तो बड़े शंकु का वक्रपृष्ठ ज्ञात कीजिए।
Solution:माना बड़े शंकु की तिर्यक ऊँचाई=5x
तथा छोटे शंकु की तिर्यक ऊँचाई=4x
बड़े शंकु का वक्र पृष्ठीय क्षेत्रफल S_1=\pi r l_1 \ldots(1)
छोटे शंकु का वक्र पृष्ठीय क्षेत्रफल S_2=400=\pi r l_2 \ldots(2)
समीकरण (1) में (2) का भाग देने पर:
\frac{S_1}{400}=\frac{\pi r l_1}{\pi r l_2} \\ \Rightarrow \frac{S_1}{400} =\frac{l_1}{l_2} \\ \Rightarrow S_1 =400 \times \frac{l_1}{l_2} \\ =400 \times \frac{5 x}{4 x} \\ \Rightarrow S_1=500 वर्गसेमी
Example:6.एक शंकु की तिर्यक ऊँचाई और त्रिज्या का अनुपात 7:4 है।यदि इसके वक्रपृष्ठ का क्षेत्रफल 792 वर्गसेमी हो,तो इसकी त्रिज्या ज्ञात कीजिए।
Solution:माना शंकु की तिर्यक ऊँचाई(l)=7x
तथा त्रिज्या (r)=4x
शंकु का वक्र पृष्ठीय क्षेत्रफल=\pi r l \\ \frac{22}{7} \times 4 x \times 7 x=792 \\ x^2=\frac{792}{22 \times 4} \\ x^2=9 \\ x=\sqrt{9} \\ x=3
शंकु के आधार की त्रिज्या (r)=4x=4×3=12 सेमी
Example:7.एक शंकु के आकार के टेन्ट की ऊँचाई 14 मीटर और आधार का क्षेत्रफल 346.5 वर्गमीटर है।यह टेन्ट 1.5 मीटर चौड़े केनवास से बना हुआ है, तो केनवास की लम्बाई ज्ञात कीजिए।
Solution:माना कि शंकु के आकार के टेन्ट की त्रिज्या=r
तथा ऊँचाई h=14 मीटर
शंकु के आधार का क्षेत्रफल=\pi r^2 \\ \Rightarrow \frac{22}{7} \times r^2=346.5 \\ \Rightarrow r^2=\frac{346.5 \times 7}{2} \\ \Rightarrow r^2=\frac{2425.5}{22} \\ \Rightarrow r^2=110.25 \\ \Rightarrow r=\sqrt{110.25} \\ \Rightarrow r=10.5 मीटर
टेन्ट की तिर्यक ऊँचाई(l)=\sqrt{h^2+r^2} \\ =\sqrt{(14)^2+(10.5)^2} \\ =\sqrt{196+110.25} \\ =\sqrt{306.25} \\ (l)=17.5 मीटर
केनवास का क्षेत्रफल=टेन्ट के तिर्यक पृष्ठ का क्षेत्रफल
=\pi r l \\ =\frac{22}{7} \times 10.5 \times 17.5 वर्गमीटर
=577.5 वर्गमीटर
केनवास की लम्बाई=\frac{\text{क्षेत्रफल}}{\text{चौड़ाई}} \\ =\frac{577.5}{1.5}=385 मीटर
Example:8.एक शंकु के आकार की त्रिज्या 14 सेमी और तिरछी ऊँचाई 105 सेमी है।शंकु का वक्र पृष्ठीय क्षेत्रफल एवं सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
Solution:शंकु के आधार की त्रिज्या (r)=14 सेमी
तथा तिरछी ऊँचाई (l)=105 सेमी
शंकु का वक्र पृष्ठीय क्षेत्रफल=\frac{22}{7} \times 14 \times 105 \\ =\frac{32340}{7} \\=4620 वर्गसेमी
शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल =\pi r(l+r) \\ =\frac{22}{7} \times 14 \times(105+14) \\ =22 \times 2 \times 119 \\ =5236 वर्गसेमी
Example:9.एक शंकु का वक्रपृष्ठ 188.4 वर्गमीटर है तथा इसकी तिरछी ऊँचाई 12 मी. है।इसके आधार की त्रिज्या ज्ञात कीजिए। (\pi=3.14 लीजिए)
Solution:शंकु का वक्रपृष्ठ का क्षेत्रफल=\pi r l=188.4 वर्गमीटर
तिर्यक ऊँचाई l=12 मीटर रखने पर:
3.14 \times r \times 12=188.4 \\ \Rightarrow r=\frac{188.4}{3.14 \times 12} \\ =\frac{188.4}{37.68} \\ \Rightarrow r=5 मीटर
Example:10.एक लम्बवृत्तीय शंकु के आधार का क्षेत्रफल 154 वर्गसेमी है।इसकी तिरछी ऊँचाई 25 सेमी है,तो शंकु की ऊँचाई ज्ञात कीजिए।
Solution:शंकु की तिरछी ऊँचाई (l)=25 सेमी
शंकु के आधार का क्षेत्रफल=\pi r^2=154 \\ \Rightarrow \frac{22}{7} \times r^2=154 \\ \Rightarrow r^2=\frac{154 \times 7}{22} \\ \Rightarrow r=\sqrt{49} =7 सेमी
शंकु की ऊँचाई
\left(h^2\right)=l^2-r^2 \\ =25^2-7^2 \\ =625-48 \\ =576 \\ h=\sqrt{576}=24 सेमी
Example:11.एक सर्कस का टेन्ट 3 मीटर ऊँचाई तक बेलनाकार है।उसके बाद ऊपरी हिस्सा शंकुनुमा है।यदि आधार का व्यास 105 मीटर और शंकुनुमा भाग की तिर्यक ऊँचाई 53 मीटर हो,तो ज्ञात कीजिए टेन्ट को बनाने में कितने वर्गमीटर कपड़ा काम में आया।
Solution:शंकु के आधार की त्रिज्या (r)=\frac{105}{2}=52.5 मीटर
तथा बेलनाकार भाग की ऊँचाई (h)=3 मीटर
बेलनाकार टेन्ट का वक्र पृष्ठीय क्षेत्रफल=2 \pi r h \\ =2 \times \frac{22}{7} \times 52.5 \times 3 \\ =\frac{6930}{7} \\ =990 वर्गमीटर
शंकुनुमा भाग की तिर्यक ऊँचाई (l)=53 मीटर
शंकुनुमा टेन्ट का वक्र पृष्ठीय क्षेत्रफल=\pi r l \\ =\frac{22}{7} \times 52.5 \times 53 \\ =\frac{61215}{7} \\ =8745 वर्गमीटर
अतः टेन्ट में लगने वाले कपड़े का कुल क्षेत्रफल=990+8745
=9735 वर्गमीटर
Example:12.शंकु के आधार की त्रिज्या और ऊँचाई क्रमशः 7 सेमी और 24 सेमी है।शंकु की तिरछी ऊँचाई,वक्रपृष्ठ का क्षेत्रफल,सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए। (\pi=\frac{22}{7} लीजिए)
Solution:शंकु की त्रिज्या (r)=7 सेमी
शंकु की ऊँचाई (h)=24 सेमी
शंकु की तिरछी ऊँचाई l=\sqrt{r^2+h^2} \\ =\sqrt{(7)^2+(24)^2} \\ =\sqrt{49+576} \\ =\sqrt{625} \\ \Rightarrow l=25 सेमी
शंकु के तिर्यक पृष्ठ का क्षेत्रफल=\pi r l \\ =\frac{22}{7} \times 7 \times 25 \\ =22 \times 25 \\ =550 वर्गसेमी
शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल=\pi r(l+r) \\ =22 \times 7 \times(25+7) \text { सेमी }^2 \\ =22 \times 32 \text { सेमी }^2 \\ =704 वर्गसेमी
Example:13.जोकर की शंकु के आकार की टोपी की त्रिज्या और तिरछी ऊँचाई का अनुपात 1:3 है।टोपी का तिर्यक पृष्ठ 462 वर्गसेमी है।इसकी तिरछी ऊँचाई ज्ञात कीजिए।
Solution:माना जोकर की टोपी की त्रिज्या r है और उसकी तिरछी ऊँचाई l=3r है।
तिर्यक पृष्ठ=\pi r l=462 \\ \Rightarrow \frac{22}{7} \times r \times 3 r=462 \\ \Rightarrow r^2=\frac{462 \times 7}{22 \times 3} \\ \Rightarrow r^2=49 \\ \Rightarrow r^2=\sqrt{49}=7 सेमी
तिर्यक ऊँचाई l=3r=3×7=21 सेमी
उपर्युक्त उदाहरणों के द्वारा शंकु का पृष्ठीय क्षेत्रफल के महत्त्वपूर्ण उदाहरण (Imp Examples of Surface Area of Cone),शंकु का पृष्ठीय क्षेत्रफल कक्षा 9 (Surface Area of Cone Class 9) को समझ सकते हैं।
3.शंकु का पृष्ठीय क्षेत्रफल के महत्त्वपूर्ण उदाहरण पर आधारित सवाल (Questions Based on Imp Examples of Surface Area of Cone):
(1.)एक लम्बवृत्तीय शंकु के वक्रपृष्ठ का क्षेत्रफल ज्ञात कीजिए जिसकी तिर्यक ऊँचाई l=10 सेमी तथा आधार की त्रिज्या r=7 सेमी हो।
(2.)यदि किसी शंकु का वक्रपृष्ठ का क्षेत्रफल वर्गसेमी है तथा उसका आधार का व्यास 14 सेमी हो तब उस शंकु की ऊँचाई ज्ञात कीजिए।
(3.)यदि शंकु की तिर्यक ऊँचाई 21 सेमी तथा आधार का व्यास 14 सेमी हो तो उसके सम्पूर्ण पृष्ठ का क्षेत्रफल ज्ञात कीजिए।
उत्तर (Answers):(1.)220 वर्गसेमी (2.)h=6 \sqrt{2} सेमी (3.)616 वर्गसेमी
उपर्युक्त सवालों को हल करने पर शंकु का पृष्ठीय क्षेत्रफल के महत्त्वपूर्ण उदाहरण (Imp Examples of Surface Area of Cone),शंकु का पृष्ठीय क्षेत्रफल कक्षा 9 (Surface Area of Cone Class 9) को ठीक से समझ सकते हैं।
Also Read This Article:- Important Examples of SA of Cylinder
4.शंकु का पृष्ठीय क्षेत्रफल के महत्त्वपूर्ण उदाहरण (Frequently Asked Questions Related to Imp Examples of Surface Area of Cone),शंकु का पृष्ठीय क्षेत्रफल कक्षा 9 (Surface Area of Cone Class 9) से सम्बन्धित अक्सर पूछे जाने वाले प्रश्न:
प्रश्न:1.शंकु के पृष्ठीय क्षेत्रफल के सूत्र लिखो। (Write the Formulas for Surface Area of Cone):
उत्तर:(1.)शंकु के आधार का क्षेत्रफल=\pi r^2
(2.)शंकु की तिर्यक ऊँचाई(l)=\sqrt{h^2+r^2}
(3.)शंकु का वक्रपृष्ठ का क्षेत्रफल=\pi r l
(4.)शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल=\pi r(l+r)
प्रश्न:2.लम्बवृत्तीय शंकु किसे कहते हैं? (What are Right Circular Cone?):
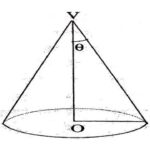
उत्तर:शंकु का आधार एक वृत्त है जिसका केन्द्र O तथा त्रिज्या OA=r (माना) है।यदि रेखा VO,आधार पर लम्ब है तो शंकु लम्बवृत्तीय शंकु कहलाता है।
प्रश्न:3.ठोस शंकु और खोखला शंकु किस प्रकार जनित होता है? (How are Solid and Hollow Cones Generated?):
उत्तर:यदि रेखाखण्ड VA और त्रिज्या OA,अक्ष VO के सापेक्ष एक पूरा चक्कर लगाए तो एक बंद आधार वाला खोखला शंकु जनित होता है।यदि \triangle VOA का क्षेत्र VO के चारों ओर परिक्रमण करता है,तो एक ठोस शंकु जनित होता है।
उपर्युक्त प्रश्नों के उत्तर द्वारा शंकु का पृष्ठीय क्षेत्रफल के महत्त्वपूर्ण उदाहरण (Imp Examples of Surface Area of Cone),शंकु का पृष्ठीय क्षेत्रफल कक्षा 9 (Surface Area of Cone Class 9) के बारे में ओर अधिक जानकारी प्राप्त कर सकते हैं।
| No. | Social Media | Url |
|---|---|---|
| 1. | click here | |
| 2. | you tube | click here |
| 3. | click here | |
| 4. | click here | |
| 5. | Facebook Page | click here |
| 6. | click here |
Imp Examples of Surface Area of Cone
शंकु का पृष्ठीय क्षेत्रफल के महत्त्वपूर्ण उदाहरण
(Imp Examples of Surface Area of Cone)
Imp Examples of Surface Area of Cone
शंकु का पृष्ठीय क्षेत्रफल के महत्त्वपूर्ण उदाहरण (Imp Examples of Surface Area of Cone)
के इस आर्टिकल में शंकु पर आधारित कुछ विशिष्ट सवालों में पृष्ठीय क्षेत्रफल ज्ञात करके
समझने का प्रयास करेंगे।
Related Posts
About Author
Satyam
About my self I am owner of Mathematics Satyam website.I am satya narain kumawat from manoharpur district-jaipur (Rajasthan) India pin code-303104.My qualification -B.SC. B.ed. I have read about m.sc. books,psychology,philosophy,spiritual, vedic,religious,yoga,health and different many knowledgeable books.I have about 15 years teaching experience upto M.sc. ,M.com.,English and science.








